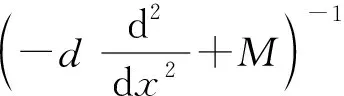一类带有内部存储和抑制剂的恒化器模型的共存解
2018-10-22李星星王治国李艳玲
李星星,王治国*,李艳玲
(陕西师范大学数学与信息科学学院,陕西西安 710119)
恒化器是用于细菌连续培养的一种实验装置.经典的恒化器模型假设细菌对营养的吸收率与自身生长率成比例,但Ketchum[1]通过实验观测到当外部养分耗尽后,细菌仍可继续生长和分裂一段时间,这表明物种的生长与内部存储营养有关.为此Droop[2]提出了带有内部存储的浮游植物生长模型来描述这一现象.Smith等[3]证明此类模型竞争排斥原理也成立.考虑到扩散现象,Hsu等[4]分析了带有扩散和内部存储模型解的共存性.
在自然界中一些微生物会产生抑制剂来增强自己的竞争力,这种现象在水生生物系统中广泛存在.Chao等[5]提出带有抗生素抑制剂的模型.Nie等[6]引入了空间异性,研究了具有内部抑制剂的反应扩散模型,分析了抑制剂对模型动力学行为的影响.然而这些模型均忽略了物种对营养的吸收存储过程,文中将研究具有内部存储和抑制剂的恒化器模型.

1 模型
在均匀搅拌环境中考虑如下恒化器模型:
(1)
式中S(t),u(t)和v(t)分别为营养物的浓度以及物种u和v在t时刻的密度;Qi(t)代表t时刻第i个物种体内每个细胞所储存的营养物浓度(i=1,2);p(t)是在t时刻抑制剂的浓度.假设v为被抑制剂影响的生物,u代表产生抑制剂的生物,S(0)是营养物的输入浓度,D为恒化器的稀释率;μi(Qi)物种生长率,依赖于细胞配额Qi;fi(S,Qi)为营养的吸收率,依赖于营养的浓度S和细胞配额Qi;Qmin,i表示细胞配额的临界值,若低于此数值物种将停止生长;函数e-μp代表抑制剂p对物种v生长率的影响程度[10],其中μ>0为常数;常数k∈(0,1)表示产生抑制剂的概率.
假设函数μi(Qi)和fi(S,Qi)满足如下条件(经典实例见文献[2,11]):

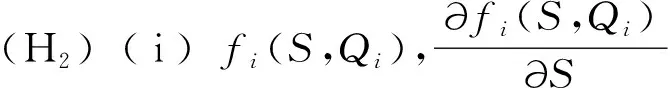
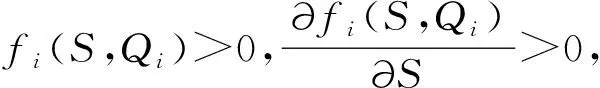
令U,V分别表示两物种储存的总营养,则U=Q1u,V=Q2v,因此在未搅拌的恒化器内,假设空间变量x∈(0,1),时间t>0,则模型(1)变为
(2)
边界条件和初始条件如下:
(3)
式中初始函数满足U0(x)≥u0(x)Qmin,1,V0(x)≥v0(x)Qmin,2,p0(x)≢0,d和γ分别为扩散系数和产出率,且均为常数.

(4)
对函数fi(S,Qi)和μi(Qi)做如下延拓:

2 准备知识
本节给出一些非线性特征值问题以及解的先验估计.在x∈[0,1]上引入以下记号:

则E,W1,W2为C0([0,1],R2)的完全锥,且E是实的正规锥.定义(u1,u2)≫E(v1,v2)当且仅当(u1,u2)-(v1,v2)∈intE.
首先在x∈(0,1)上考虑非线性特征值问题
(5)
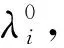
下面考虑单物种u与总营养U的边值问题
(6)

对具有内部存储的单物种模型
(7)
引理2设(u,U,v,V)是系统(4)的非负解,且u≢0,U≢0,v≢0,V≢0,则
( i )u>0,U>0,v>0,V>0;
( ii )U+V (iii)Qmin,1u 其中Q1≥Qmin,1,S=z(x)-U-V,以及 根据Q*1定义可知 f1(z(x),Q*1)-(1-k)μ1(Q*1)Q*1≤0. 由( i )得S=z-U-V f1(S,Q*1)-(1-k)μ1(Q*1)Q*1<0. 令H1(x)=U(x)-Q*1u(x),则H1(x)满足 (H1)x(0)=(H1)x(1)+γH1(1)=0 及如下不等式: 下面利用度理论研究系统(4)正解的存在性,为此引入以下空间: 其中 且满足 其中ξ1(Q1)和ϑ1(Q1)分别由(8)式和(9)式给出,ξ2(Q2)和ϑ2(Q2)分别满足 显然F在CB[0,1]中是紧的. 方程(4)有非负解等价于F在N内有正不动点.F的所有平凡和半平凡非负不动点包括(0,0,0,0),(u*,U*,0,0)和(0,0,v*,V*),为了使用度理论,需要计算F在这些非负不动点邻域上的指标. 引理3当λ≥1时,F(u,U,v,V)=λ(u,U,v,V)在W中不存在解满足||u||+||U||+||v||+||V||=R0. 证明设(u,U,v,V)∈W满足F(u,U,v,V)=λ(u,U,v,V)且||u||+||U||+||v||+||V||=R0,则 令y=z-U-V,则y满足 (10) 由极值原理可得y≥0,x∈[0,1],即U+V≤z(x).根据(u,U,v,V)∈W可得U≥uQmin,1,V≥vQmin,2.因此 即F(u,U,v,V)=λ(u,U,v,V)在W中不存在解满足||u||+||U||+||v||+||V||=R0. 】 证明根据引理3和文献[14]引理12.1( i )可证. 】 令O+(u*,U*,0,0)和O+(0,0,v*,V*)分别表示(u*,U*,0,0)和(0,0,v*,V*)在W中的邻域.下面计算F在O+(u*,U*,0,0)和O+(0,0,v*,V*)上的指标.在x∈(0,1)上引入特征值问题 证明由于( i )和( ii )的证明完全类似,这里仅给出( i )的证明.定义 其中 则算子方程F(t)(u,U,v,V)=(u,U,v,V)在x∈(0,1)上等价于 (13) 若(u,U,v,V)是F(t)在∂O+(u*,U*,0,0)上的不动点,则u>0,U>0,v≥0,V≥0.由最大值原理得v>0,V>0,否则(u,U,v,V)=(u*,U*,0,0),此与(u,U,v,V)∈∂O+(u*,U*,0,0)矛盾. 下证对任意的t∈[0,1],F(t)在∈∂O+(u*,U*,0,0)上没有不动点.假设(u,U,v,V)∈∂O+(u*,U*,0,0)是F(t)的不动点,则u>0,U>0,且v>0,V>0.当t=0时,方程如下: (14) (15) 类似可证(u*,U*,0,0)是F(0)在O+(u*,U*,0,0)上的唯一不动点.因此 对于τ∈[0,1],定义 其中 则T(τ)(u,U,v,V)=(u,U,v,V)在x∈(0,1)上满足 类似可证T(τ)在∂O+(u*,U*,0,0)上没有不动点,且易得F(0)=T(0),T(1)=T1×T2,其中 根据拓扑度的同伦不变性和乘积定理可得 因此(u,U)是系统(6)的上解.由单调方法和(u*,U*)的唯一性可得u≥u*,U≥U*,这与||u||+||U||=δ0矛盾.因此,index(T1,Pδ0,W1)=0.又因为(u,U)=(u*,U*)是T1在PδPδ0上的唯一不动点,所以 由λ≥1可得(v,V)满足微分不等式 (16) 根据(16)式易得(v,V)是如下抛物问题在x∈(0,1),t>0上的下解: (17) (18) (19) (20) 综上所述, 然而由引理4~6计算可得以下矛盾表达式: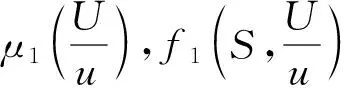
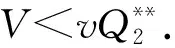
3 正解存在性