基于元胞自动机的小学生群体应急疏散仿真研究
2018-10-22李兴莉
白 洋,李兴莉,郭 芳
(太原科技大学应用科学学院,太原 030024)
近年来,随着经济发展和社会进步,各类诸如交通堵塞、踩踏事故频繁发生,交通流动力学的研究日益引起国内外的广泛关注[1-2]。相比车辆交通流,行人存在自主性、随机性、能动性等特点,比车辆交通流更为复杂,更具有挑战性。一般来说,行人流微观疏散模型可以分为为三种:社会力模型[3-4],元胞自动机模型[5-8]以及格子气模型[9-11]。元胞自动机通过模拟或定义系统中简单的个体微观行为特性,在个体之间相互作用的条件下,实现系统整体宏观行为特征的研究和模拟仿真,因其易于计算机模拟计算,被广泛用于模拟交通流和行人流。2001年Burstedde等首次提出了“背景场”的概念,建立了完全不依赖于交通流理论的二维元胞自动机行人流模型[12]。赵宜宾等针对学生群体的的主观智能作用,引入出口影响因子概率、目标方向密度概率、移动方向校正因子三个因素对疏散过程的影响,建立了基于元胞自动机模型的多出口人员疏散模型[13]。陈亮等研究了教室内带有写字板的培训椅对疏散效率的影响[14]。董力耘等基于动态背景场的更新,考虑教室内桌椅的排列对学生疏散过程中的路径选择行为的影响[15]。
通过调研发现,目前对学生群体的研究,主要集中在以下几个方面:小规模疏散演习(或可控的疏散实验)的实验研究和建立模型(或软件)的数值模拟对比研究[12],评价不同布局下的疏散效率[13-14]及突发事件下学生心理的定性分析[16]。这些研究中涉及的对象几乎全是大学生。事实上,面对突发事故,大学生和一般行人的心理行为更为接近,而小学生则表现出更易于一般行人的更为复杂的心理行为特征,从媒体的报告中可看出各种频发的校园踩踏事故主要集中在小学。因此,建立能合理描述小学生群体疏散行为的模型,探讨疏散特性及规律具有重要的现实意义。
1 模型
模型建立在一个尺寸为L×L的二维正方形网格离散网格内,一个网格代表一个元胞,用障碍物占据系统边界元胞构成房间围墙,在墙上留有的空格元胞为房间的出口,其宽度为W.元胞可被行人占据或为空,大小取0.4 m×0.4 m,图1中圆点表示行人,箭头表示向出口方向移动。行人在系统中的初始密度为ρ,行人的疏散仿真过程被离散化为相等的时间步长,在每个时间步长中,行人根据规则,做出一定的移动或者原地等待,且行人的移动不能穿越和跨越围墙,离开房间只能通过安全出口,疏散后的行人不会重新进入系统。

图1 一般场景模拟示意图
Fig.1 Diagram of general spot simulation
心理学研究发现,紧急状况下个体行为主要表现为:恐慌、迅速逃离、冲动、从众、超越他人。对于小学生群体,除具有一般行人的行为特点,还具有其自身特有的行为特征:活波、好动、缺乏对危险的预见性、相互推搡挤压现象严重。将这些特点与小学生紧急疏散相结合,一方面考虑在疏散过程中移动速度会不自觉增加,另一方面引入挤压人数比例描述挤压程度,发生挤压的人数越多,挤压程度越高。
本文在元胞自动机模型的基础上采用Moore型邻域,如图2(a)所示。在疏散模型的一个时间步长中,行人本可以选择周围8个方向进行移动或者待在原地。考虑到房间只有一个出口,这里假设不考虑小学生的后退行为,将Moore型邻域更新为图2(b).
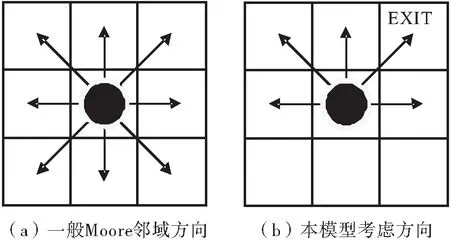
图2 Moore邻域方向示意图
Fig.2 Directions of Moore adjacent region
小学生群体在移动时需先考虑相邻区域的位置危险度,基于此引入位置危险度来解决小学生运动路线的选择策略问题,以“人员以最快时间,最短距离到达最安全的位置”为原则建立。位置危险度定义如下:
d(i,j)=
(1)
式中(i,j)和(x,y)分别代表格点的位置和坐标,(x0,y0)为出口坐标。通过比较邻域内各个点的位置危险度,位置危险度最小的格点就是行人移动的目标格点,若最小的格点已被占据,则行人静止不动。为便于描述,将图2(b)所示扩展的Moore二邻域分为两个区域,如图3所示,定义(a)所示阴影区域为相隔区域,(b)所示阴影部分区域为相邻区域。在计算危险度时,只有相邻区域位置的危险度d(i,j)≠时,才可以计算其对应相隔位置的危险度。换言之,即行人要移动到相隔区域必须具有移动到相邻区域的可能性。

图3 扩展Moore型邻域
Fig.3 Extended Moore adjacent region
考虑到小学生群体的差异性,将学生群体分为A类和B类,A类(见图10中向右三角形)表示小学生的心理承受能力较强,在疏散过程中较理智,始终不会与其他学生发生冲突或挤压;B类(见图4(a)中向左三角形)表示心理承受能力较弱的小学生群体,在运动过程中会和其他B类学生发生推搡或挤压,挤压后两个B类学生处于同一元胞位置,将其称为元胞C,用菱形表示(见图4(b)).
考虑B类小学生群体运动过程中的推搡、挤压,在移动时B类小学生的相邻区域若被其他B类小学生占据且其Moore领域内无空元胞位置时,则相邻区域内被B类小学生占据的元胞位置可以看成是空元胞,计算其危险度,若危险度小于B类小学生所在位置危险度,则两个B类小学生会共同占据同一元胞,合成一个挤压元胞C,且C不向相隔区域移动,如图4所示。

图4 B类人更新规则示意图
Fig.4 Diagram of B-class updating rules of squeezing cell C
若C类元胞在运动过程中其相邻区域有空元胞位置,则分别计算各个空元胞位置的危险度,并与所处元胞位置的危险度进行比较,若空元胞位置的危险度小于所在位置的危险度,则挤压元胞C分为两个B元胞,且一个留在相邻区域危险度小的元胞位置,另一个留在C原来所在的位置,如图5所示。若A或B类元胞在其相邻区域内有C类元胞存在,则A或B元胞在此时间步静止不动。
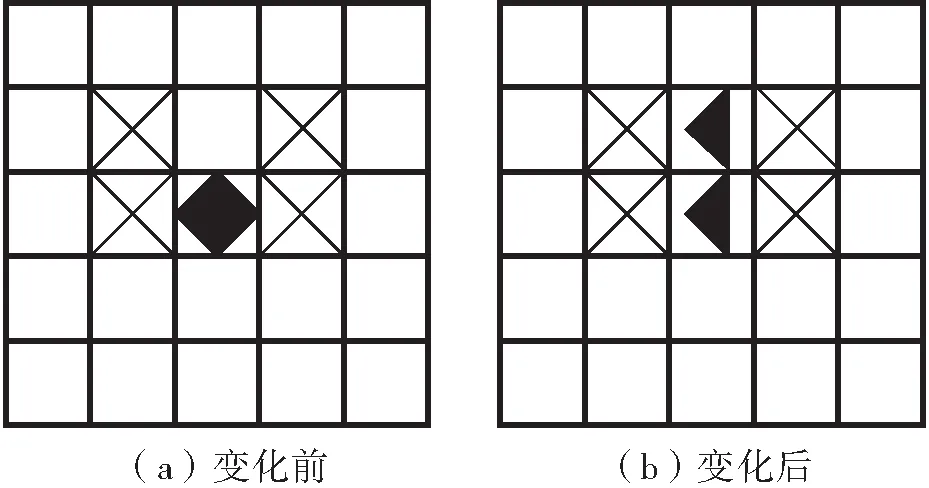
图5 挤压元胞C更新规则示意图
Fig.5 Diagram of updating rules of squeezing cell C


图6 移动方向和位置示意图
Fig.6 Diagram of moving directions and locations
模型的具体移动规则如下:
(1) 给定区域内行人随机的初始分布,并在每一时间步中,确定各个元胞的位置危险度;
(2) 根据所在元胞距出口的距离,依次进行移动,离出口近的先移动;
(3) 进行位置更新;
(4) 当所有元胞在一时间步内更新完毕,下一时间步重新计算各个元胞的危险度;
(5) 以上步骤重复到所有人离开系统。
2 数值模拟与分析
初始时刻行人随机分布在二维的网格系统中,模拟过程中采用随机序列并行的方式按上述规则进行位置更新,通过更改B类人在初始时刻的比例a,模拟疏散过程中拥挤情况对疏散时间的影响。参数设置如下:L=30,W=3,小学生密度为ρ.定义系统中学生的平均速度:
其中c为计算的次数,Nn为此某一时间步房间内的总人数,vi(t)为某一时间步内单人的速度。为了减少随机性对结果的影响,取50个样本做系统平均。
图7给出了学生密度为ρ=0.1,0.3,0.5,0.7时,不同B类学生比例下疏散总人数N和疏散时步T的关系。可以看出,当ρ=0.1时,随着a的增大,疏散总人数随时间的变化曲线几乎重合,如图7(a)所示;随着密度的增大,挤压群体所占的比例越大,疏散效率急剧下降,如图7(b)-(d)所示。特别是密度增大到0.7时,挤压人数80%下的疏散效率相对无挤压人数的疏散效率下降了近70%,这个结果表明,在低密度下,学生移动灵活,与周围学生发生挤压的概率较小,对疏散效率的影响可以忽略;在中高密度下,B类人初始比例不同,疏散的时间也不相同,a越小,挤压发生的可能性就越低,行人的疏散时间越短,疏散效率越高,反之则效率越低,局部挤压对疏散效率的影响越明显。

图7 疏散总人数N和疏散时步T的关系
Fig.7 Curves of evacuation total number of people N changing with evacuation time step T
图8给出了初始密度为ρ=0.1,0.3,0.5,0.7时,系统内小学生群体的平均速度V与疏散时步T的关系。可以看出,在初始阶段,平均速度最大;随着时间的推移,平均速度逐渐变慢,并在某一值的周围出现波动,其波动幅度取决于a值的大小,a越大,波动幅度越大,且密度ρ越大,波动幅度差异越明显;疏散后期大部分小学生被疏散出系统,此时群体之间的挤压减小直至趋于正常状态,a=0.9时的平均速度与a=0时疏散后期的平均速度大小接近,直到疏散完毕平均速度归零。这是因为在演化的初始阶段,房间内小学生都尽可能以较快的速度向出口方向移动,平均速度较大,随着小学生向出口位置聚集,局部密度增加,平均速度逐渐变慢并出现上下波动,a值越大,拥挤程度越高,平均速度相对较低,而在疏散后期,随着系统内学生不断减少,挤压对疏散的影响越来越小,且随着密度的增大,上述所有特征越明显。
为了进一步描述挤压程度对疏散效率的影响,图10给出了不同人群密度ρ下C元胞的数量随演化时步的变化关系。在疏散初始,C元胞数量均为0,系统内部不存在推搡挤压现象;随着时间的推移,挤压元胞C的数量开始上升,在某个时步达到最大值,随后逐渐减少最后归于0.C元胞的数量取决于人群初始密度ρ和B类人初始比例a,且与ρ、a呈正相关。C元胞数量上升因为所有人都向门口移动形成拥挤,之后逐渐下降是由于系统学生不断减少,所以数量达到最大值后逐渐减小,直到为0,结论进一步证实了图8的结论。

图8 平均速度V和疏散时步T的关系图
Fig.8 Curves of average speed V changing with evacuation time step T

图9 挤压元胞C数量Nc与疏散时步T图
Fig.9 Curves of squeezing cell C changing with evacuation time step T

图10 密度ρ=0.5时空演化斑图
Fig.10 Evolving pattern of time and space withρ=0.5
最后图10给出了ρ=0.5时小学生在a=0,0.9的时空演化斑图。在演化的初始阶段,学生群体均向出口位置聚集,并在出口处形成类似于“拱”状的拥堵瓶颈。正常疏散情况下,小学生在出口位置聚集形成拥堵,呈“拱形”消散(如图10(a)-(c)所示),该情况描述的是小学生在出口位置理性的排队疏散,并依次离开系统,疏散效率较高。相反,当B类人所占的比例a=0.9时,小学生群体之间行人之间相互推搡挤压,造成系统内部压力增大,在相同时步下,系统内留有的学生人数明显多于正常情况(图10(c)和(f)).
3 结论
为了研究应急疏散情况下小学生群体的心理特征对疏散行为和效率的影响,本文建立了一种描述含挤压行为的小学生群体紧急疏散元胞自动机模型。数值模拟得到以下结论:(1) 在低密度下,发生推搡挤压的人数对疏散效率的影响可以忽略,而在中高密度情况下,推搡挤压人群所占的比例的增大将会导致疏散效率显著下降;(2) 推搡挤压的人数比例越大,疏散过程中拥挤程度越高,平均速度越小;(3) 挤压人数与小学生初始密度呈正相关。随着时间的增加,挤压人数增多,且挤压人数在达到峰值后人数减少,直至最后变为0.
