基于改进节点收缩法的加权供应链网络节点重要度评估

刘 娜，沈 江，于鲲鹏，刘爱军，王钰莹



基于改进节点收缩法的加权供应链网络节点重要度评估

刘 娜1, 2，沈 江1，于鲲鹏3，刘爱军4，王钰莹1

(1. 天津大学管理与经济学部，天津 300072；2. 石河子大学机械电气工程学院，石河子 832000； 3. 中国海洋大学管理学院，青岛 266100；4. 西安电子科技大学经济与管理学院，西安 710071)

为了全面客观地评估供应链网络中节点的重要度，有效识别供应链网络中关键节点，提升供应链网络的稳定性．本文基于复杂网络理论，提出一种融合节点自身重要度及连边重要度的改进加权节点收缩法，此改进方法能够全面客观地评估供应链网络节点之间的重要度；最后以变压器装配生产供应链网络为例，实验结果验证了该改进算法的合理性和有效性．

供应链网络；节点重要度；脆弱性；三角模糊数

近年来，随着市场竞争的加剧和产品生命周期的缩短，越来越多的企业选择以联合研发的方式来优势互补，增强核心竞争力，从而形成以供应链网络形式参与市场竞争[1-3]．供应链网络中各企业充分利用自身优势，相互协作并共同服务于终端客户．然而，企业在享受供应链网络带来便利的同时，也面临一定的风险．例如广州汽车制造业，其主要以生产Honda、Nissan和Toyota等车型为龙头，由日本本土供应发动机等核心部件，并由中国供应商提供其他相关部件或原材料，形成以跨国区域为主的供应链协作网络．而2011年日本的“3.11”地震造成日本本土大面积停电，导致日本的汽车等关键零部件供应链断裂，同年4月广汽生产总值下降幅度高达32.2%[4].再如2000年3月，位于美国的新墨西哥州的飞利浦公司某工厂发生火灾，由于该厂所生产的芯片为爱立信手机的关键部件，致使爱立信手机供应链中断，直接经济损失高达4亿美元[5]．上述种种由地震、火灾等不确定性因素带给供应链网络沉重冲击的现实，使得人们开始思考供应链网络如此脆弱的根本原因．现有供应链网络脆弱性的辨识方法较多，不同学者从不同角度对供应链网络脆弱性做了相应研究．

谭跃进等[6]根据节点自身重要度提出复杂网络节点重要度评估的节点收缩法，此方法认为供应链网络中最为重要的节点就是将该节点收缩后凝聚度最大的节点；于鲲鹏等[7]针对节点收缩法无法对供应链网络节点之间相互影响关系量化表示等问题，采用改进的节点收缩法，设计了一套新的供应链网络脆弱性分析方法；周漩等[8]针对节点收缩法、节点删除法、介数法的不足，提出了一种利用重要度评价矩阵来评估网络节点重要度的方法；Singh等[9]引入图形傅里叶转换中心(graph Fourier transform centrality，GFT-C)来量化复杂网络中节点的重要性；赵海等[10]采用节点删除法来解决互联网AS级中中心节点难以确定等问题，然而上述研究仅注重对节点自身重要度的计算而忽略其网络拓扑特性或者与其邻域节点连边的重要程度．此外，还有部分学者在研究供应链网络节点重要度时，充分考虑了节点之间的拓扑结构，例如阮逸润等[11]针对以往复杂网络节点重要度计算没有考虑网络结构随着时间变化而变化等问题，提出了一种考虑节点度以及邻域节点拓扑重合度的节点重要性评估算法；Hu等[12]提出了节点重要性贡献相关矩阵(NICCM)方法用于对网络节点重要度进行评估，其中节点重要度不仅取决于相邻节点还包括网络中非相邻节点；Blackhurst等[13]提出融合Petri网和三角聚类算法的供应链网络脆弱性评估方法，该方法适用于对复杂供应链网络的脆弱性进行评估，且同时能够有效缓解因供应链网络局部断裂而造成的冲击，然而上述方法仅侧重于计算网络节点重要度及邻边节点重要度，而忽略了供应链网络中各节点之间的影响关系，而实际供应链网络中上下游企业通常以不同形式给予联系，且各个相邻节点之间的影响程度不同．

综上所述，本文提出一种改进的加权节点收缩法来评估供应链网络节点的重要度，此方法在原有节点收缩法基础上充分考虑节点自身及连边重要度．此外，在计算节点重要度时，充分考虑不同节点企业之间的供应类型及影响程度，并采用三角模糊数的方法对节点间的影响程度进行量化，此过程中融入了不同专家对节点企业的偏好程度．该改进方法在一定程度上能够较为合理客观地反映供应链网络的真实情况，并有效克服节点收缩法、节点删除法、介数法计算节点重要度时的弊端，使得加权供应链网络节点重要度评估更为全面、客观、准确．

1 供应链网络节点重要度与脆弱性描述

脆弱性是鲁棒性的反面，是指在考虑网络拓扑结构的情况下，当供应链网络中某一节点或者连边受到扰动时，对整个网络性能的影响程度[14]．通常供应链网络脆弱性与网络节点的重要度紧密相关，其中“重要度”被定义为网络中节点或者连边的存在对整个网络部分或者全连通特性的影响程度．在此背景下，当该节点重要度越大则认为其是网络中最为脆弱的元素．供应链网络外部市场的多变性及复杂性使得网络中节点较易受到扰动，且带给供应链网络一定的冲击．基于此，有必要对供应链网络中各个节点重要度进行分析，以鉴别出重要度较大的节点并对其进行控制和改善，本文研究内容对于保证供应链网络的顺利运行以及提高供应链网络的抗毁性和可靠性具有重要意义．

2 供应链网络脆弱性分析

2.1 节点收缩法计算网络凝聚度

此方法在评估节点重要度时，将待测节点与其相连的所有节点收缩为一个节点，通过比较不同节点收缩之后的凝聚度来衡量节点的重要度[15]．通常某节点凝聚度越大，则认为该节点越重要．图1所示为节点收缩过程．

图1 节点收缩过程

通常在供应链网络中，节点凝聚度计算公式为

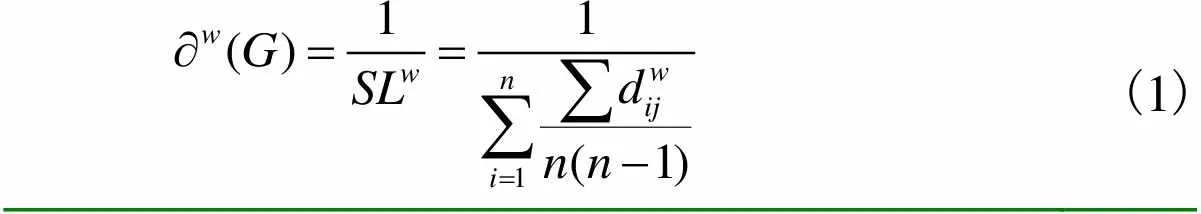
 (1)

2.2 节点间关联性量化计算

对于网络节点重要度的评估，大部分学者仅针对无权网络进行分析[8-9]，但无权网络仅反映节点的连接方式或网络结构的拓扑特性，并不能有效描述节点间的相互影响程度，而供应链网络中各节点企业之间采用不同形式给予传递(例如原材料、零部件、技术服务等)且节点间影响程度不同，显然上述无权网络节点重要度评估方法不适用于本文中供应链网络的节点重要度评估．基于此，本文充分考虑供应链网络中节点企业之间的影响程度，并深入分析不同节点与邻域节点之间的影响程度的差异，最终采用基于三角模糊数的专家打分法确定节点间关联紧密程度作为加权供应链网络连边的权重．采用三角模糊数的专家打分法能够体现专家对网络中各个节点和连边的评估重要度，并将专家的模糊信息给予准确量化表示，在一定程度上能够合理反映节点与其相应连边的综合重要度．其主要包含如下步骤：首先将各个专家的模糊语义信息转化为三角模糊数，然后将三角模糊数转换为清晰值[16-17]．具体步骤如下．

本文将模糊语义变量根据各个节点之间影响程度的强弱分为如表1所示的5个等级，并将各等级转化为三角模糊数形式．

表1 模糊语义变量及三角模糊数

Tab.1 Fuzzy semantic variables and triangular fuzzy numbers

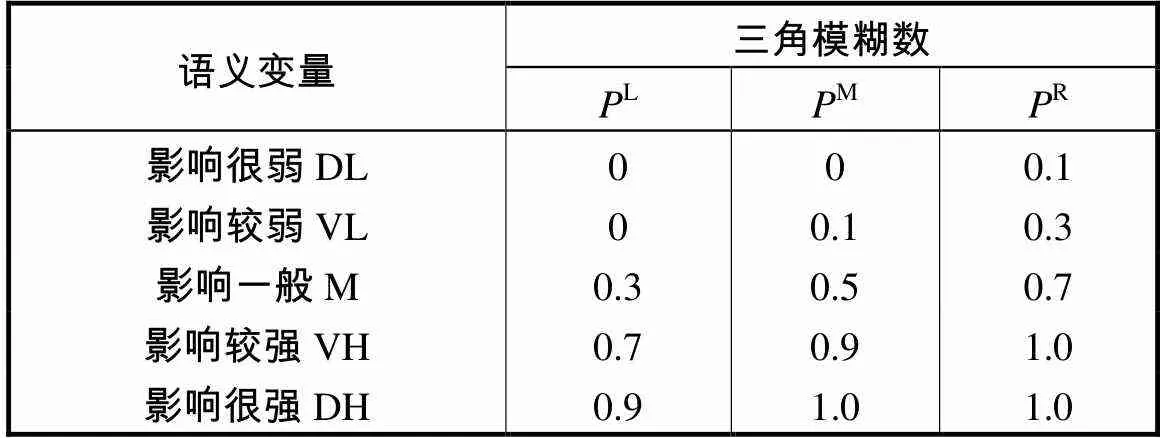
语义变量三角模糊数 PLPMPR 影响很弱DL000.1 影响较弱VL00.10.3 影响一般M0.30.50.7 影响较强VH0.70.91.0 影响很强DH0.91.01.0

步骤2 采用加权方法集结各个专家对不同影响程度的偏好信息.

由于不同专家对节点间影响关系强弱的判断存在差异，且随着决策问题复杂化及专家的个人喜好等原因导致同一影响关系对于不同专家描述不同，因此本文充分考虑各专家的偏好信息．

 (2)

步骤3 计算评判期望值.

 (3)

 (4)

 (5)

2.3 加权改进节点收缩法计算节点重要度

在供应链网络中，上下游企业之间采用不同的供应类型相互联结，例如原材料、服务、技术支持等，假如任何一个环节出现问题都会影响其后续供应环节的顺利开展，例如上述爱立信手机生产供应链中原材料受到扰动，使得后续生产、组装、销售等环节遭受严重影响．因此，在供应链网络中，节点重要度不仅包括其节点自身重要度，而且需考虑邻域节点关联重要度．基于此，本文在加权节点收缩法计算网络节点重要度的基础上，充分考虑其邻域节点间关联关系重要度，此改进方法有效克服了传统节点收缩法仅考虑自身重要度的缺陷[18]，其节点重要度计算公式为

图2 一种简单的供应链网络

 (6)

 (7)

 (8)

 (9)

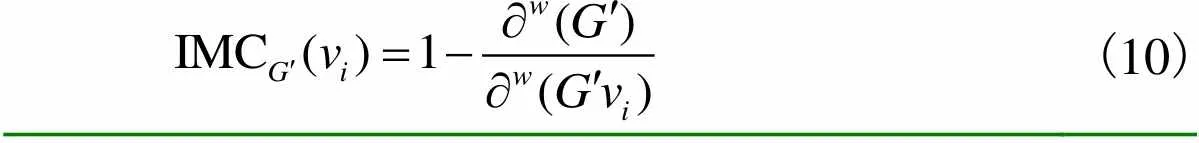
 (10)

经过式(6)～(10)计算之后的节点重要度由于考虑了节点自身重要度和连边重要度，因此计算得出的结果可能大于1，还需对其进行归一化处理得

 (11)

上述加权改进节点收缩法计算供应链网络节点重要度充分考虑了网络中节点自身重要度及其邻域节点关联关系重要度，并采用三角模糊数方法量化计算节点之间的供应关系影响程度，此改进方法能够全面客观地评估网络节点的重要度，为整个供应链网络脆弱性分析提供一种新的分析思路．

2.4 算法步骤

综上所述，该改进算法的步骤如图3所示.

图3 加权供应链网络节点重要度计算步骤

3 案例分析

本文选取国内某知名变压器公司典型的(330～500,kV)/(750～1,000,kV)油浸式电力变压器生产供应链为研究对象，对其供应链网络节点重要度和网络脆弱性进行研究．本文结合变压器各部件结构，绘制如图4所示变压器供应链网络，其中此变压器中套管、调压开关、风扇等为外协件，而在本文中将其虚拟为一供应链节点，图4充分考虑两种型号变压器供应链网络的拓扑结构．根据图4中变压器供应链结构，并结合复杂网络基础理论，绘制如图5所示供应链网络拓扑结构．

图4 某企业(330～500,kV)/(750～1,000,kV)油浸式电力变压器生产供应链

图5 (330～500,kV)/(750～1,000,kV)型油浸式电力变压器供应链网络拓扑结构

1) 供应链网络节点之间的权重计算

表2 专家打分结果

Tab.2 Results of experts evaluation

表3 变压器供应链网络节点影响程度量化结果

Tab.3 Results of transformer supply chain network node influence degree

2) 加权网络节点自身重要度

3) 加权网络邻域节点重要度

4) 对比实验及结果分析

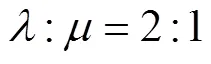
表4 变压器供应链网络节点自身重要度

Tab.4 Node importance of the transformer supply chain network

表5 变压器供应链网络邻域节点间连边重要度

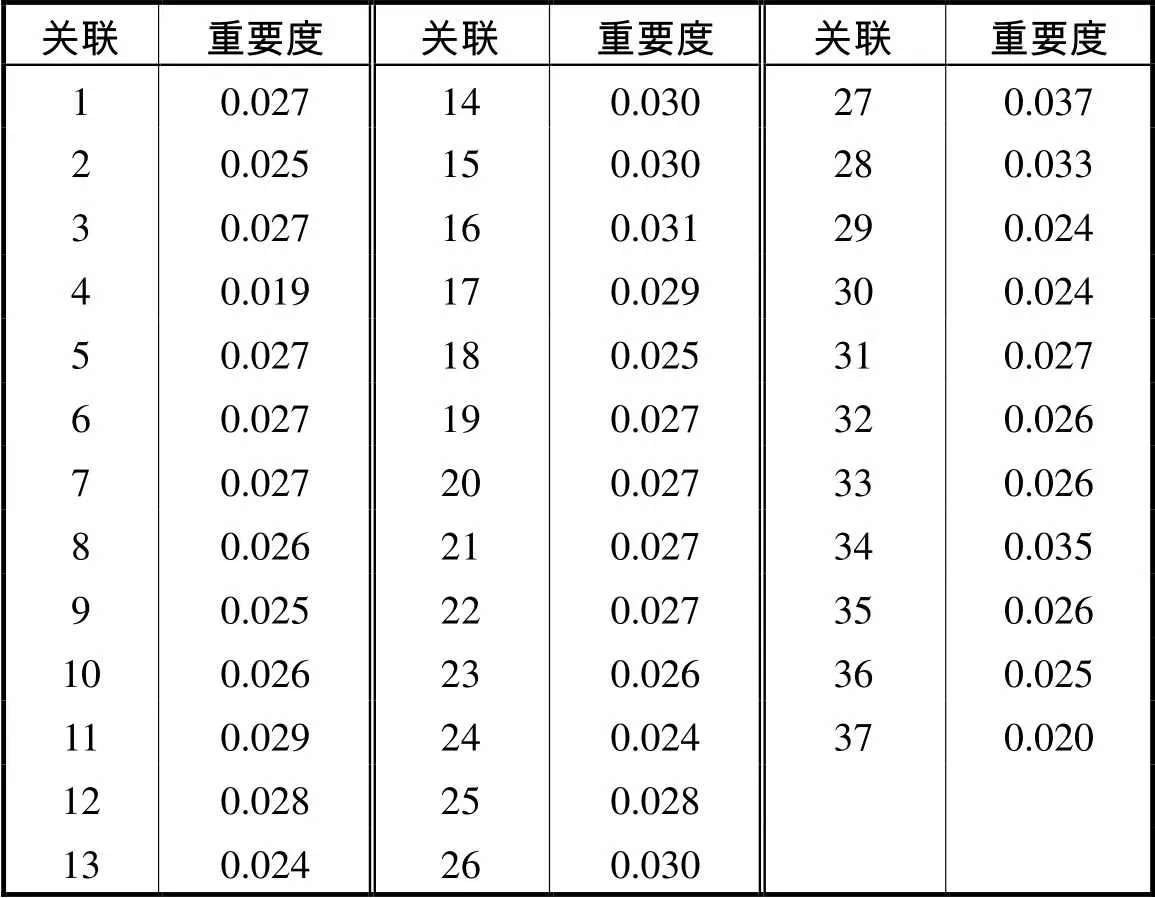
Tab.5 Neighborhood node connection importance of the transformer supply chain network

表6 变压器供应链网络节点重要度结果对比

Tab.6 Comparison of node importance of transformer supply chain network

5) 参数敏感性分析

从上述分析结果可知，本文方法较其他两种方法更为优越，因此本文方法能够较为合理、客观地对供应链网络节点重要度进行评估．

图6 不同比例系数下节点重要度

4 结 论

(1) 本文在基于复杂网络基础上，全面客观地研究了供应链网络节点重要度评估方法及网络整体脆弱性，为供应链网络脆弱性分析及增强其抗风险能力提供参考．

(2) 计算供应链网络节点重要度时充分考虑了节点自身重要度和连边重要度．供应链网络为一整体连通的网络，其内部各个节点之间通过一定的关联关系进行联结，且各个关联重要度不同，因此本文结合现实供应链网络实际情况，充分考虑供应链网络节点自身重要度及连边重要度．

(3) 深入剖析供应链网络节点企业之间的供应类型及影响程度，并采用基于专家打分法融合三角模糊数对各网络节点之间的影响关系进行量化，此过程中融入专家对供应链网络节点企业的偏好程度，在一定程度上能够较为客观地反映供应链网络的真实 情况．

(4) 本文最后以国内某知名变压器生产商两种型号油侵式变压器装配为例进行仿真实验，结果显示本文所提出的方法能够较为合理有效地对供应链网络节点自身重要度进行评估，与此同时此改进方法能够为供应链网络脆弱性研究提供新的分析思路．

［1］ Bleda J，Mehta P，Sanghvi P. Architecting the supply chain of the future[EB/OL]. http://www.accenture.com/ cn-en/insight-architecting-future-supply-chain，2017-11-23.

［2］ Blackhurst J，Rungtusanatham M J，Scheibe K，et al. Supply chain vulnerability assessment：A network based visualization and clustering analysis approach[J].，2018，24(1)：21-30.

［3］ Saban K，Mawhinney J R，Drake M J. An integrated approach to managing extended supply chain networks [J].，2017，60(5)：689-697.

［4］ Guangzhou Statistics Bureau. Macroeconomic database system[EB/OL]. http：//www. gzstats. gov. cn/tjsj，2011-05-14.

［5］ Nofa S Y，Morelb G，Monostoric L，et al. From plant and logistics cintrol to multi-enterprise collaboration[J].，2006，30(1)：55-68.

［6］ 谭跃进，吴俊，邓宏钟. 复杂网络中节点重要度评估的节点收缩方法[J]. 系统工程理论与实践，2006，26(11)：79-83.

Tan Yuejin，Wu Jun，Deng Hongzhong. Evaluation method for node importance based on node contraction in complex networks[J].，2006，26(11)：79-83(in Chinese).

［7］ 于鲲鹏，杨 育，刘 娜，等. 基于加权改进节点收缩法的供应链网络脆弱性分析[J]. 计算机集成制造系统，2014，20(4)：963-970.

Yu Kunpeng，Yang Yu，Liu Na，et al. Vulnerability of complicated supply chain network based on weighted improved nodes contraction method[J].，2014，20(4)：963-970(in Chinese).

［8］ 周 漩，张凤鸣，李克武，等. 利用重要度评价矩阵确定复杂网络关键节点[J]. 物理学报，2012，61(5)：050201-050206.

Zhou Xuan，Zhang Fengming，Li Kewu，et al. Finding critical node by node importance evaluation matrix in complex networks[J].，2012，61(5)：050201-050206(in Chinese).

［9］ Singh R，Chakraborty A，Manoj B S. GFT centrality：A new node importance measure for complex networks [J].：，2017，487：185-195.

［10］ 赵 海，贾思媛，艾 均，等. 互联网AS级拓扑中心化度量方法[J]. 东北大学学报：自然科学版，2012，33(9)：1248-1252.

Zhao Hai，Jia Siyuan，Ai Jun，et al. Research on centralized measurement method of internet AS-level topology[J].：，2012，33(9)：1248-1252(in Chinese).

［11］ 阮逸润，老松杨，王竣德，等. 基于领域相似度的复杂网络节点重要度评估算法[J]. 物理学报，2017，66(3)：365-373.

Ruan Yirun，Lao Songyang，Wang Junde，et al. Node importance measurement based on neighborhood similarity in complex network[J].，2017，66(3)：365-373(in Chinese).

［12］ Hu P，Fan W，Mei S. Identifying node importance in complex networks[J].：，2015，429：169-176.

［13］ Blackhurst J，Rungtusanatham M J，Scheibe K，et al. Supply chain vulnerability assessment：A network based visualization and clustering analysis approach[J].，2018，24(1)：21-30.

［14］ Liu H，Tian Z，Huang A，et al. Analysis of vulnerabilities in maritime supply chains[J].，2018，169：475-484.

［15］ 孙玺菁，司守奎. 复杂网络算法与应用[M]. 北京：国防工业出版社，2016.

Sun Xijing，Si Shoukui.[M]. Beijing：National Defense Industry Press，2016(in Chinese).

［16］ Wang J，Ding D，Liu O，et al. A synthetic method for knowledge management performance evaluation based on triangular fuzzy number and group support systems [J].，2016，39(C)：11-20.

［17］ Molinari F. A new criterion of choice between generalized triangular fuzzy numbers[J].2016，296(C)：51-69.

［18］ 于鲲鹏，刘爱军，苏加福. 基于UWNC的互联网经济时代企业价值网络稳定性研究[J]. 科学学与科学技术管理，2017，38(9)：80-90.

Yu Kunpeng，Liu Aijun，Su Jiafu. Research on the stability of enterprise value network based on the UWNC in the age of internet economy[J].，2017，38(9)：80-90(in Chinese).

(责任编辑：孙立华)

Weighted Supply Chain Network Node Importance Assessment Based on Improved Node Contraction Method

Liu Na1, 2，Shen Jiang1，Yu Kunpeng3，Liu Aijun4，Wang Yuying1

(1．College of Management and Economics，Tianjin University，Tianjin 300072，China； 2．School of Mechanical and Electrical Engineering，Shihezi University，Shihezi 832000，China； 3．College of Management，Ocean University of China，Qingdao 266100，China； 4．College of Economics and Management，Xidian University，Xi’an 710071，China)

To comprehensively and objectively evaluate node importance in the supply chain network and effectively identify the key nodes so as to enhance its stability，an improved node contraction method that combines the importance of nodes and the connected edges is proposed based on complex network theory．This moved method can evaluate the importance of supply chain network nodes comprehensively and objectively. Taking transformer assembly and manufacturing supply chain network as an example，the validity and effectiveness of the proposed method are verified by experimental results.

supply chain network；node importance；vulnerability；triangular fuzzy number

10.11784/tdxbz201712023

N949

A

0493-2137(2018)10-1056-09

2017-12-15；

2018-04-19.

刘 娜（1986—  ），女，博士研究生，讲师，naliu188@126.com．

沈 江，motoshen@163.com.

国家自然科学基金资助项目(71571105)；石河子大学应用基础青年研究资助项目(2015ZRKXYQ-LH06).

the National Natural Science Foundation of China(No.,71571105)and the Applied Basic Youth Research Program of Shihezi University(No.,2015ZRKXYQ-LH06).