基于网格与韦泊统计特性的立体图像质量评价

侯春萍，林洪湖



基于网格与韦泊统计特性的立体图像质量评价

侯春萍，林洪湖

(天津大学电气自动化与信息工程学院，天津 300072)

针对立体图像失真会改变图像对比度、边缘和结构等信息的特性，提出一种无参考立体图像质量评价方法．首先，利用韦泊分布的尺度参数和形状参数分别描述合成图、左右视图及视差图的梯度图像特征；然后用网格强度及其规律性分别描述合成图、左右视图及视差图的网格图像特征；最后，将所得特征输入支持向量回归(SVR)网络中训练模型，获得特征到质量分数之间映射关系的模型，从而预测立体图像质量．通过利用LIVE-3D I数据库和LIVE-3D Ⅱ数据库进行性能测试，证明了本文提出的方法与人眼视觉特性具有很高的一致性，且性能优于目前主流的图像质量评价算法．

立体图像质量评价；韦泊分布；网格特征；支持向量回归

图像在处理、存储和传输中产生的失真严重影响了人们对图像的理解，同时也影响了图像有效信息的提取，因此建立有效的图像质量评价机制至关重要．客观图像质量评价方法分为全参考图像质量评价(FR-IQA)、部分参考图像质量评价(RR-IQA)和无参考图像质量评价(NR-IQA)．FR-IQA方法主要计算参考图像与失真图像的结构相似性[1]、信息保真 度[2]、特征相似性[3]或多尺度结构相似性[4]．尽管这些全参考型图像质量评价能较好地预测图像质量，但在实际应用中往往无法得到作为参考的原始图像．RR-IQA方法需要从参考图像中提取部分特征信息．NR-IQA方法仅从失真图像中提取有关特征以评价图像质量[5-6]．鉴于参考图像通常难以获得，因此在图像质量评价方法中，NR-IQA更具价值．

结构特征在图像质量评价中非常重要[7-8]，Wang等[1]基于图像亮度、对比度和结构相似度提出了结构相似性对图像质量进行描述；基于人眼在不同距离观察对图像感知效果不同这一特性，Wang等[4]结合多尺度框架提出多尺度结构相似性；大多数算法都从图像亮度和对比度等角度考虑图像结构，而网格图对结构的描述能力一直鲜有人发现，Li等[9]提出基于网格特征的JPEG图像块效应NR-IQA算法，通过描述图像中块效应网格的强度和规律性生成相应分数．考虑到图像结构失真和边缘像素变化等会造成图像梯度幅值(gradient magnitude，GM)变化，文献[10]考虑了梯度域上的韦泊统计特征对图像结构的影响．

立体图像质量评价与平面图像质量评价的主要差别在于立体图像存在视差信息，因此影响了人眼对图像质量舒适度的感知[11]．文献[12]直接通过双目融合特征评价3D图像质量，Lin等[13]提出应用2D方法评价左右视图并直接加权后得到3D图像质量．Shao等[14]提出在合成图基础上通过模拟视觉皮层感知、学习双目感知域特性[15]、利用特征编码模拟初级视觉皮层特性[16]或用DNN来模拟双目竞争[17]实现立体图像质量评价．文献[18]提取合成图幅度和相位特征实现立体图像质量评价；综上所述，从合成图中提取的特征可以在一定程度上反映立体图像 失真．

本文借鉴了文献[9]中网格特征对图像结构的影响及文献[10]中韦泊统计特性在梯度图上的表现的思想，同时考虑了合成图在立体图像质量评价中的重要作用，针对失真立体图像质量评价，结合网格特征和韦泊统计特性来描述图像结构和边缘信息，提出了一种新的基于网格和韦泊统计特性的立体图像质量评价方法．

1 立体图像质量评价模型

本文提出的无参考图像质量评价模型主要包含3步：①计算视差图及合成图；②提取左右视图、视差图及合成图中的特征；③将特征图像输入到质量预测模型中进行图像质量评价．具体流程如图1所示．

图1中，先由失真立体图像对计算视差图并生成合成图；将左右视图、视差图及合成图均转换到梯度域，用韦泊分布的形状参数和尺度参数描述梯度图像特征，同时也计算各图的网格图，用网格强度和网格规律性描述网格特征；将所得特征输入SVR中建立模型预测立体图像质量．考虑到人眼在观察图像时，由于观察的尺度空间的变化，同一图像在不同尺度空间会产生不同的视觉效果，为了更精确地预测图像质量，因此本文还分别对左右视图、合成图和视差图均进行两次降采样处理，从采样图中提取网格特征及韦泊统计特征．

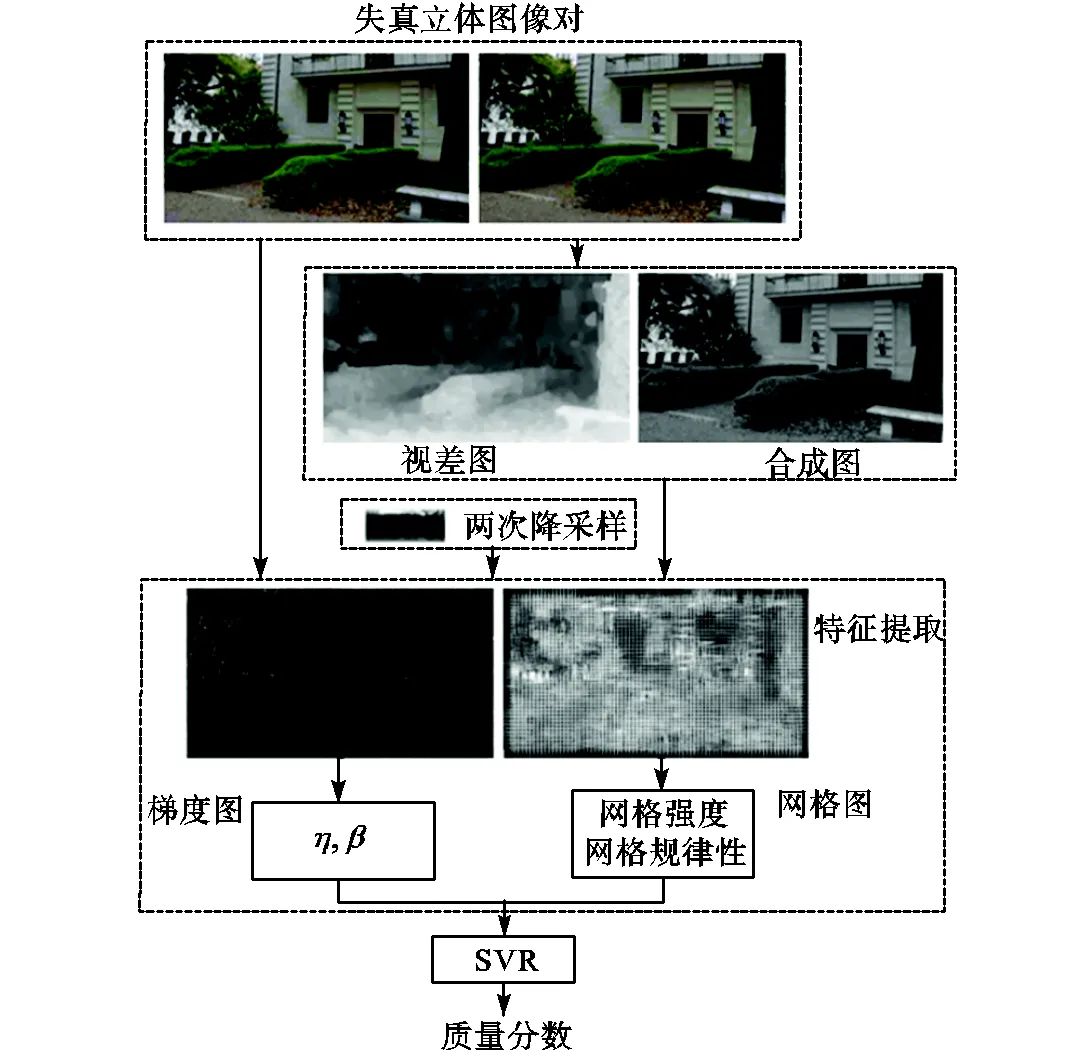
图1 算法流程

1.1 生成合成图

融合视差信息的立体图像与平面图像不同，仅通过对左右图像质量求均值得到的立体图像客观质量的方法效果不明显，因此本文考虑增加融合了视差信息的合成图及视差图对立体图像进行评价．

利用左右视图及其视差计算合成图，公式为

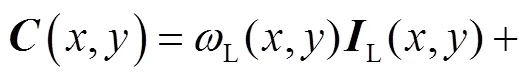
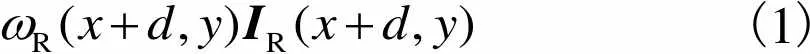
     (1)

式中：表示合成图；()表示位置；为视差；L、R分别表示左视图和右视图；L和R为左右权重．

左右权重通过归一化Gabor能量响应赋值得到

   (2)

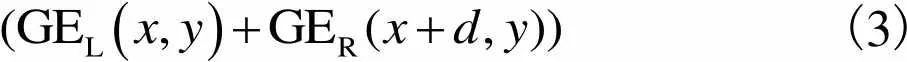
   (3)

式中GEL、GER分别为Gabor能量响应值．Gabor滤波能量响应是Gabor滤波器4个方向(水平、垂直、两对角线)的幅值响应能量之和．Gabor滤波器方向的幅值(，，)可通过二维复Gabor滤波器得 到，即

(4)

式中：∈{L，R}；*表示卷积；为二维复Gabor滤波器；为滤波方向．二维复Gabor滤波器定义为

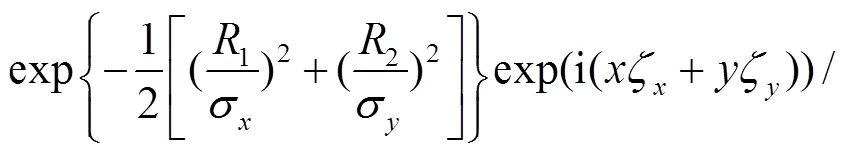
(5)

式中：1＝cos＋sin；2＝-sin＋cos；σ、σ是标准差；ζ、ζ为空间频率，其值设为3.67,cycle/degree．

1.2 韦泊统计特征

韦泊分布与人类对图像的视觉有很强的相关性，失真图像的梯度幅值遵循韦泊分布[19]，Scholte等[20]也认为人类视觉系统与韦泊分布的形状和尺度参数相关度高．本文借助了文献[19]和[20]提出的韦泊分布思想，考虑了韦泊分布的形状和尺度参数对图像的空间一致性和复杂度描述的精确性，提出在梯度域使用韦泊分布的形状和尺度参数描述图像失真．韦泊分布形状和尺度参数可由其概率密度函数得到，韦泊分布的概率密度函数定义为

 (6)

式中：和分别表示形尺度参数和形状参数；M是图像的梯度幅值，灰度图像的M计算公式为

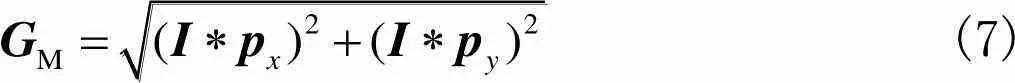
 (7)

式中：和分别表示沿水平和垂直方向的Prewitt滤波算子．定义为

 (8)

 (9)

式(6)中代表分布宽度的尺度参数能够反映局部对比度，而局部对比度变化影响人眼对图像质量的感知；形状参数是指分布的峰值，对局部边缘空间频率比较敏感．为阐释和能反映人眼能感知图像质量失真，本文通过图2和图3来说明和对不同失真类型图像的影响．

图2是LIVE-3D I数据库的一幅原始左视图及其5种失真类型图像，失真类型分别是：快衰弱(fast fading，FF)，高斯模糊(Gaussian blur，Gblur)，高斯白噪声(Gaussian white noise，GWN)，JPEG压缩和JP2K压缩．

图3中(a)和(b)分别是图2中不同失真类型图像在不同失真强度下韦泊分布的尺度参数和形状参数的分布图，其中横坐标为图像失真程度，随着坐标轴数字的增大失真也随之变得严重，图3(a)中纵坐标是韦泊尺度参数，图3(b)中纵坐标是韦泊形状参数．从图中可以看出：不同失真类型韦泊统计参数的分布不同，对于JPEG、JP2K、Gblur和FF来说，随着失真程度的增加，边缘弱化、对比度减小，因此韦泊分布的形状参数及尺度参数随之逐渐减小；但是对于高斯白噪声而言，受噪声污染后局部边缘变化使得韦泊分布宽度增加且峰值增大，韦泊分布的形状参数及尺度参数随图像失真程度增大而逐渐增大．由图3(a)和(b)可知，对同一幅原始图像而言不同失真类型的图像梯度域的韦泊分布参数明显不同．且参数随着失真程度的增加而呈现规律性变化，因而韦泊分布的和两个参数能够描述图像失真．

图2 不同失真类型图像

图3 不同失真类型在不同失真强度下的韦泊参数分布

1.3 网格强度及网格规律性

仅仅依靠和参数还不能很好地描述图像的结构等信息受失真的影响，因此本文提取网格特征描述图像结构和边缘等特征，通过结合韦泊统计特征和网格特征描述不同尺度下图像的结构信息，以获得更好的图像质量预测效果．网格特征需要从网格图中提取，本节先介绍失真图的网格图像．

1.3.1 网格图像

通过对图像求梯度来描述像素不连续性的做法存在不足．为更好描述像素不连续性，本文首先提取相对独立的网格图像，再从中提取特征．

定义网格图像为

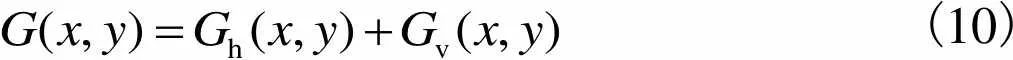
 (10)

式中：h(，)和v(，)分别表示水平网格和垂直网格，考虑到失真图像中含有JPEG压缩图像，JPEG编码的块大小为8像素×8像素，本文提取周期为8的水平网格及垂直网格．其公式为

   (11)

   (12)

式中：median(·)表示取中值；h(，)、v(，)表示利用滤波处理后的相邻水平、垂直边缘之和减去其中值，即

     (13)

     (14)

式中：a(，)、b(，)为水平、垂直边缘信号处理后相邻几列之和．水平、垂直边缘信号经过处理后，为增强较弱水平、垂直边缘信号，选取相邻几列累加．但是累加列的个数大小会影响提取的网格特征，避免选取过大或过小的情况，本文参考文献[9]中对信号的分析，选取每33列相累加，即

 (15)

 (16)

式中：h、v分别为利用二阶差分计算的灰度图像的水平及垂直边缘处理后的信号，处理前的信号为

 (17)

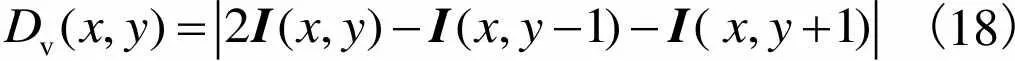
 (18)

式中(，)为灰度图像．

考虑到图像失真如块效应等失真强度比边缘强度弱很多[9]，为了减轻图像本身边缘的影响，设置一个阈值对边缘信号进行处理，即

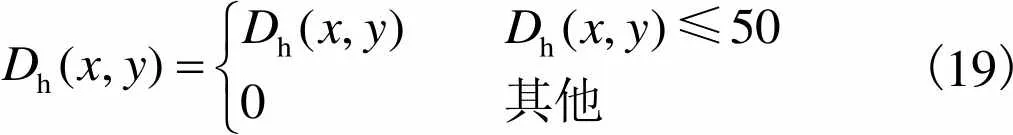
 (19)

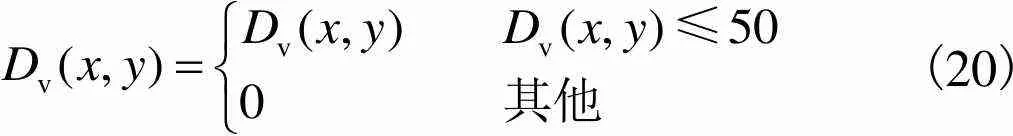
 (20)

1.3.2 网格强度及网格规律性

定义网格强度为

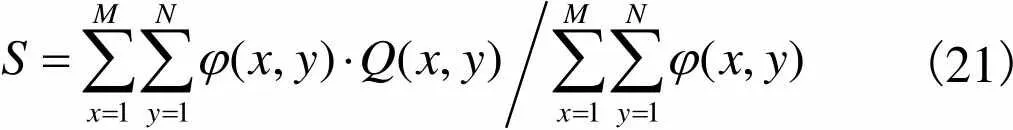
 (21)

式中：×是图像的大小；(，)＝(，)；(，)是权值函数．

考虑到人眼在观察图像时对非平坦区域的结构失真较为敏感，而由于存在纹理掩盖效应，人眼不容易观察到纹理区域的失真，因此本文为人眼对图像敏感区及不敏感区网格图加上不同权值．为使式(21)的权值函数(，)对平滑区域的网格强度值赋予较大的权值，对纹理区域的网格强度赋予较小的权值，定义权值函数(，)为

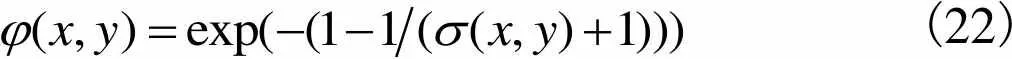
 (22)

式中(，)表示原始图像中像素(，)邻域像素的标准差，用于描述纹理复杂度．

为强化对图像结构失真和边缘变化的描述能力，考虑网格规律性．将网格规律性定义为

 (23)

式中：h和v分别为水平方向和垂直方向网格规律性度量．本文只介绍h垂直方向网格规律性度量v可由类似方法获得．h定义为

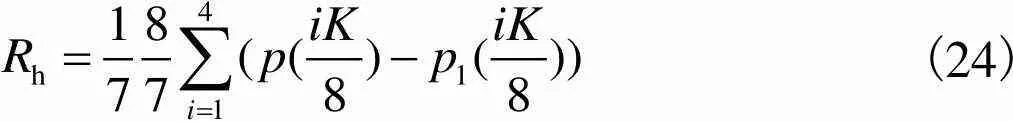
 (24)

式中：是网格图像经离散付里叶变换后的功率谱的均值；1为进行中值滤波后的功率谱；系数8/7主要用于保持总体能量；1/7用于计算功率谱的平均峰值．

网格图像经离散傅里叶变换并求功率谱的过程如下．

先利用权值函数(，)对网格图像加权和归一化处理．

   (25)

加权后的网格图像G转换为一维信号，并表示为h．计算相邻元素差值为

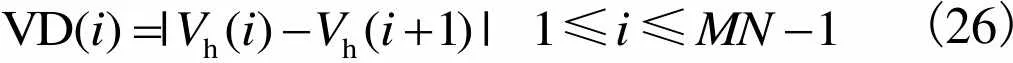
 (26)

上文提到，网格信号的周期为8，因此差值信号VD的周期也为8，将周期信号记为s．

 (27)

 (28)

则功率谱的均值为

 (29)

经中值滤波后得1，将和1代入式(24)即得水平方向网格规律性度量．

图4和图5分别是同一幅图像的5种失真类型图像在不同失真程度下的网格强度分布图和网格规律性分布图，由图4和图5可以看出两点：①不同失真类型的图像网格强度和网格规律性分布图均不相同；②不同失真类型的图像网格强度和网格规律性分布图变化趋势不尽相同．对于JPEG压缩而言，图像失真越严重，网格强度越大，网格规律性越明显；对于WN而言，无论图像失真程度如何，网格强度和网格规律性基本无变化；对于Gblur而言，随着图像失真程度增加，网格强度随之降低，网格规律性也减弱；对JP2K和FF而言，图像失真程度增加，网格强度和网格规律性先增强后减弱；通过图4和图5可以进一步说明由网格强度和网格规律性描述的图像结构可以很好地反映不同类型的图像失真．

图4 不同失真程度下网格强度

图5 不同失真程度下网格规律性

1.4 图像质量预测

本文对左右视图、合成图及视差图均进行两次降采样变换到不同尺度空间，分别提取每个信号的韦泊统计特征(形状参数和尺度参数)及网格强度和网格规律性特征．对图像进行两次降采样处理时，共提取特征数为48个．特征提取后，需要一个回归模型将各特征映射为表示图像总体质量的分数，本文采用以径向基核作为核函数的SVR作为映射函数[21].本文所提出的无参考图像质量评价算法的支持向量回归模型分为训练部分和测试部分．在训练部分中，对提取的图像特征和其对应主观评分值应用SVR进行网络训练．在测试部分，将提取出的图像特征输入到已训练好的网络中，输出预测的质量分数．

2 实验结果及分析

2.1 数据库和评价指标介绍

本文提出的算法利用2个公开的图像质量数据库进行了性能测试，数据库包括LIVE-3D I和LIVE-3D Ⅱ．LIVE-3D I包含 365 幅失真立体图像及20 幅原始图像，均是左右失真程度相同的对称失真，包含5种失真类型：JPEG 压缩、JPEG2000(JP2K)、Gblur、WN以及FF．LIVE-3D Ⅱ包含 360 幅失真立体图像及8幅原始图像，包括对称和非对称2种失真，每种失真方式包括5种失真类型：JPEG、JP2K、Gblur、WN、FF．

本文采用国际通用图像质量评价算法性能指标：皮尔森线性相关系数(Pearson linear correlation coefficient，PLCC)、斯皮尔曼排序相关系数(Spearman rank-order correlation coefficient，SRCC)和均方根误差(root-mean-squared error，RMSE)．SRCC指标衡量客观算法的预测单调性，PLCC和RMSE指标衡量客观算法的预测准确性．SRCC和PLCC的值越接近1及RMSE的值越小，则算法性能越好，图像客观预测质量分数与主观质量分数相关性越高．

2.2 特征融合模型

本文分别基于LIVE-3D I数据库和LIVE-3D Ⅱ数据库，利用SVR网络构建立体图像质量评价模型测试本文的算法性能．无参考立体图像质量评价模型采用核函数为径向基函数的-SVR支持回归向量机，建立模型及算法测试具体步骤如下．

步骤1 在每个数据库中随机选取80%,的图像作为训练集，剩余20%,的图像作为测试集．

步骤２ 输入训练集图像特征及对应图像的主观质量分数值，利用SVR网络进行训练，获得特征到主观质量分数的映射关系模型；对测试集图像，利用得到的模型进行立体图像质量预测．分别计算SRCC、PLCC和RMSE值．

步骤３ 重复步骤1和步骤2 1,000次，分别对1,000次测试得到的SRCC、PLCC和RMSE值取均值作为最终的SRCC、PLCC和RMSE值，用作算法性能比较参数．

2.3 算法比较和分析

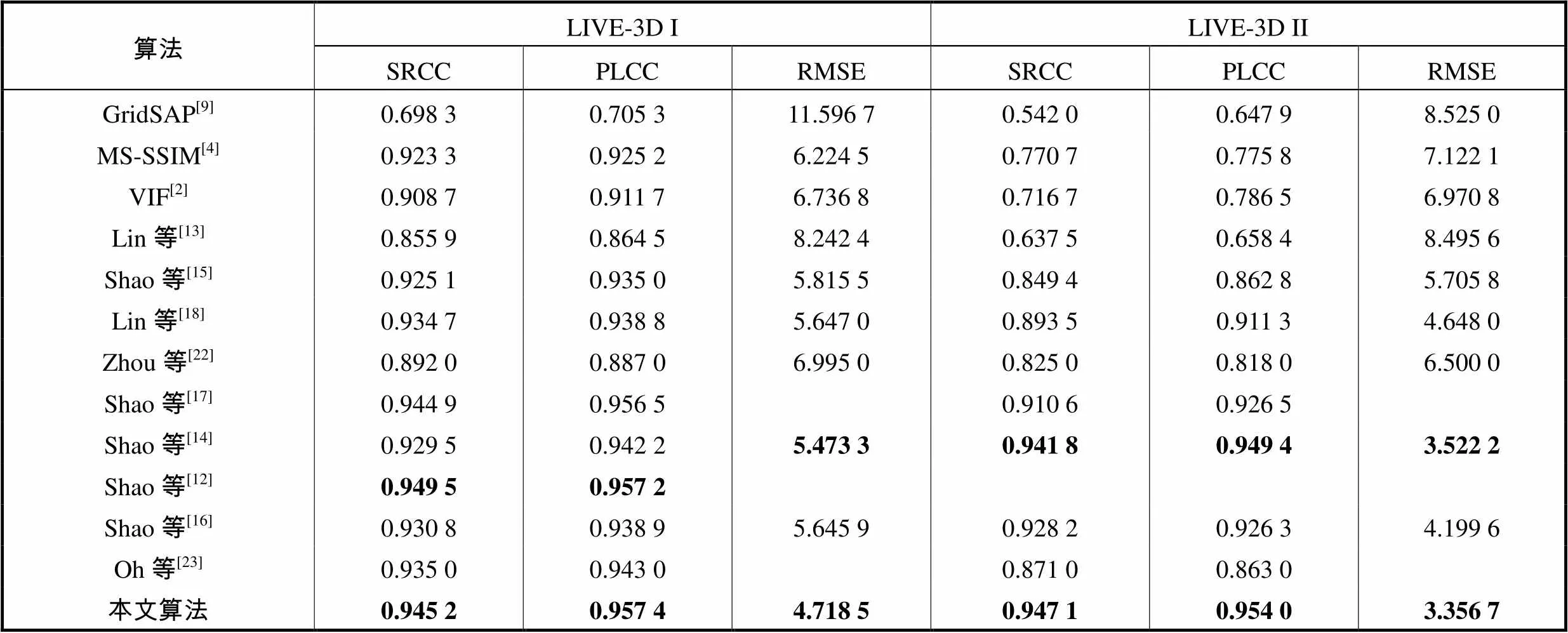
表1给出了本文提出的算法与主流的图像质量评价算法性能的比较结果．比较算法包括VIF[2]、MS-SSIM[4]、GridSAP[9]、Lin等[13]、Shao等[15]、Lin 等[18]、Zhou等[22]、Shao等[17]、Shao等[14]、Shao  等[12]、Shao等[16]、Oh等[23]，其中MS-SSIM、VIF、GridSAP为2D图像质量评价算法，将其分别对左右视图进行图像质量预测，再取均值作为3D图像质量预测分数．为了方便观看，表1中用加粗字体表示性能最高的2个算法．

从表1中可以看出：①本文算法在LIVE-3D Ⅰ数据库和LIVE-3D Ⅱ数据库上的总体性能都优于其他算法，具有很高的准确性，在LIVE-3D Ⅰ中本文算法的PLCC是目前所有立体图像质量评价算法中最高的，比文献[12]的算法高出0.000,2，而SRCC仅次于文献[12]，在LIVE-3D Ⅱ中本文算法性能指标均优于所有其他立体图像质量评价算法；②因为LIVE-3D I数据库只包含对称失真，LIVE-3D Ⅱ数据库既包含对称失真又包含非对称失真．所以其他算法用LIVE-3D Ⅰ数据库计算得到的性能总是明显优于利用LIVE-3D Ⅱ数据库计算得到的性能．而本文算法在2个数据库上的性能相当；相反，在LIVE-3D Ⅱ数据库上的SRCC值略高于LIVE-3D Ⅰ数据库上的SRCC值．为验证本算法在不同失真类型立体图像上的性能，本文算法还分别对LIVE-3D Ⅰ数据库的5类失真图像逐一进行质量分数预测，与各算法的对比结果如表2，从表2中可以看出，本文算法总体优于其它算法，本文算法对JP2K、WN、Gblur三种失真图像均有很高的主客观一致性．

本文算法在梯度域提取韦泊统计特征，同时提取相对独立的网格特征．韦泊统计特征反映了图像中像素的变化，而像素变化与图像边缘有直接关系；仅仅依靠韦泊分布的形状参数和尺度参数还不能很好地描述图像的结构等信息受失真的影响，网格特征可以反映图像结构和边缘等信息．本文综合考虑韦泊统计特征和网格特征对图像结构和边缘等信息的影响，将二者有机结合起来对立体图像质量进行评价．实验结果证明梯度域韦泊统计特征及网格图像中的网格强度和网格规律性特征可以很好地描述图像结构失真和边缘变化．

表1 算法性能比较

Tab.1 Performance comparison of algorithms

表2 在单一失真类型的LIVE-3DI数据库上比较不同算法的性能

Tab.2 Performances comparison on LIVE-3D I database with signal distortion

2.4 图像降采样的影响

观看图像时，随着尺度空间的增加，图像会变得越来越模糊，反映了人眼和图像距离变化时，图像在人眼视网膜上的成像变化．降采样能够模拟人眼在不同距离观看图像时产生不同的视觉效果，本文对左右视图、合成图及视差图分别进行1次、2次、3次、4次降采样及不进行降采样，在LIVE-3D I数据库和LIVE-3D II数据库进行性能测试，由表3可以看出，在LIVE-3D I数据库中4次降采样比两次降采样效果略优；在LIVE-3D II数据库中，当图像不进行降采样时，效果最差，随着降采样次数增加，效果越来越好，降采样两次时本文算法性能达到最佳，此后随着降采样次数增加，效果下降．实验结果说明并非降采样次数越多越好，当达到一定次数时图像已经严重失真，从所得采样信号提取的网格特征和韦泊统计特征已不能很好描述图像结构失真和边缘变化．综合实验结果表明两次降采样能够使本算法达到更好的预测结果．

表3 不同降采样次数性能比较

Tab.3 Performance comparison of different downsamplings

3 结 语

本文提出一种在视差图上提取韦泊统计特征和网格特征的无参考立体图像质量评价方法．将在左右视图、合成图和视差图上提取的特征输入SVR网络训练，得到训练模型，以实现特征到质量分数的映射，性能优于目前的立体图像质量评价算法．未来本算法将拓展到视频质量评价．

［1］ Wang Zhou，Bovik A C，Sheikh H R，et al. Image quality assessment：From error visibility to structural similarity[J].，2004，13(4)：600-612.

［2］ Hamid R S，Bovik A C. Image information and visual quality[J].，2006，15(2)：430-444.

［3］ Zhang Lin，Zhang Lei，Mou Xuanqin，et al. FSIM：A feature similarity index for image quality assessment[J].，2011，20(8)：2378-2386.

［4］ Wang Zhou，Simoncelli E P，Bovik A C. Multiscale structural similarity for image quality assessment[C]//200437，Pacific Grove，USA，2003：1398-1402.

［5］ Yue Guanghui，Hou Chunping，Gu Ke，et al. No reference image blurriness assessment with local binary patterns[J].，2017，49：382-391.

［6］ Yue Guanghui，Hou Chunping，Gu Ke，et al. Biologically inspired blind quality assessment of tone-mapped images[J].，2018，65(3)：2525-2536.

［7］ Yue G，Hou C，Jiang Q，et al. Blind Stereoscopic 3D image quality assessment via analysis of naturalness，structure，and binocular asymmetry[J].，2018，150：204-214.

［8］ 侯春萍，林洪湖. 基于小波变换与结构特征的立体图像质量评价[J]. 激光与光电子学进展，2018，55(6)：061005.

Hou Chunping，Lin Honghu. Stereoscopic image quality assessment based on wavelet transform and structure characteristics[J].，2018，55(6)：061005(in Chinese).

［9］ Li Leida，Zhou Yu，Wu Jinjian，et al. GridSAR：Grid strength and regularity for robust evaluation of blocking artifacts in JPEG images[J].，2015，30：153-163.

［10］ Deng Chenwei，Wang Shuigen，Li Zhen，et al. Content-insensitive blind image blurriness assessment using Weibull statistics and sparse extreme learning machine[EB/OL]. https://ieeexplore.ieee.org/document/796 7621/，2017.

［11］ Yue Guanghui，Hou Chunping，Lei Jianjun，et al. Optimal region selection for stereoscopic video subtitle insertion[EB/OL]. https://ieeexplore.ieee.org/document/ 80104501/，2017.

［12］ Shao Feng，Li Kemeng，Lin Weisi，et al. Using binocular feature combination for blind quality assessment of stereoscopic images[J].，2015，22(10)：1548-1551.

［13］ Lin Yu-Hsun，Wu Ja-Ling. Quality assessment of stereoscopic 3D image compression by binocular integration behaviors[J].2014，23(4)：1527-1542.

［14］ Shao Feng，Chen Wanting，Lin Wenchong，et al. Simulating receptive fields of human visual cortex for 3D image quality prediction[J].，2016，55(21)：5488-5496.

［15］ Shao Feng，Li Kemeng，Lin Weisi，et al. Full-reference quality assessment of stereoscopic images by learning binocular receptive field properties[J].，2015，24(10)：2971-2983.

［16］ Shao Feng，Chen Wanting，Jiang Gangyi，et al. Modeling the perceptual quality of stereoscopic images in the primary visual cortex[J].，2017，5：15706-15716.

［17］ Shao Feng，Tian Weijun，Lin Weisi，et al. Toward a blind deep quality evaluator for stereoscopic images based on monocular and binocular interactions[J].，2016，25(5)：2059-2074.

［18］ Lin Yancong，Yang Jiachen，Lu Wen，et al. Quality index for stereoscopic images by jointly evaluating cyclopean amplitude and cyclopean phase[J].，2017，11(1)：89-101.

［19］ Geusebroek Jan-Mark，Arnold W. M. Smeulders. Fragmentation in the vision of scenes[C]//Tokyo，Japan，2003：130-135.

［20］ Scholte HS，Ghebreab S，Waldorp L，et al. Brain responses strongly correlate with Weibull image statistics when processing natural images[J].，2009，9(4)：29-29.

［21］ Scholkopf B，Smola A J.：，，，[M]. Cambridge：MIT Press，2001.

［22］ Zhou Wujie，Yu Lu，Qiu Weiwei，et al. Utilizing binocular vision to facilitate completely blind 3D image quality measurement[J].，2016，129：130-136.

［23］ Oh H，Ahn S，Kim J，et al. Blind deep S3D image quality evaluation via local to global feature aggregation[J].，2017，26(10)：4923-4936.

(责任编辑：王晓燕)

Stereoscopic Image Quality Assessment Based on Grid and Weibull Statistics

Hou Chunping，Lin Honghu

(School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China)

Stereoscopic image distortion will change the contrast，edge，structure and other information of image．To solve the problem，a no-reference stereoscopic image quality estimator was proposed．First，the gradient image characteristics of the cyclopean image，left and right view and disparity map were parameterized using(scale parameter)andshape parameter)of Weibull distribution．Second，the grid characteristics of image were described by grid strength and regularity．Finally，the model described the relationship between the acquired features and scores was trained by support vector regression(SVR)network，which was used to predict the stereoscopic image quality．Experimental results on LIVE-3D I and LIVE-3D Ⅱ show that the proposed method is highly correlated with the human visual system and superior to the mainstream state-of-the-art IQA metrics.

stereoscopic image quality assessment；Weibull distribution；grid characteristic；support vector re gression

the Key International(Regional)Cooperative Research Program of National Natural Science Foundation of China (No.,61520106002) and the National Natural Science Foundation of China(No.,61471262).

TN919.8

A

0493-2137(2018)10-1015-08

10.11784/tdxbz201710002

2017-10-03；

2018-04-11.

侯春萍（1957— ），女，博士，教授，hcp@tju.edu.cn.

林洪湖，linhonghu@tju.edu.cn.

国家自然科学基金重点国际(地区)合作研究资助项目(61520106002)；国家自然科学基金资助项目(61471262).