基于MIMLNN的玉米蛋白质功能预测
2018-10-22陈彦明
陈彦明
(上海海事大学信息工程学院,上海 201306)
0 引言
谷物及其制品,提供了人类40%-70%的食品[1],玉米是世界上最主要的谷物,大约1万年墨西哥南部的土著人首先种植了玉米[2],现今玉米已成为世界许多地区的主食,总产量超过小麦、大米。然而,并不是所有的玉米都直接被人类消费,一些玉米用于生产乙醇、动物饲料和其他玉米产品,如玉米淀粉和玉米糖浆。谷类对人体健康有非常重要的积极影响,玉米中的纤维素和植物化学素等成分对人体而言具有良好的营养保健作用。
对玉米的蛋白质功能进行注释以便对它功能蛋白的生理意义进行理解,对于玉米蛋白质组学的研究显然非常重要。在世界上较为主流的蛋白质序列数据库中,已有一定量的经人工注释复核的玉米蛋白质数据可供使用,但同时仍有大量未经注释且功能未知的玉米蛋白质序列。面对这些没有经过注释且功能未知的玉米蛋白质,显然手工注释的方法已经跟不上数据的脚步,非常需要一种自动化的方法来对玉米的蛋白质进行功能预测。
在这样的时代背景下,不管是从玉米蛋白质研究的角度来说,还是从玉米对于我国经济社会发展的重要性来说,研究使用计算机技术实现对玉米的蛋白质自动化地进行功能预测具有不言而喻的现实意义。而机器学习技术的兴起发展为解决此类问题提供了一种优秀的解决方案,其中一部分技术则非常适合解决此类预测问题。
1 算法概述
多示例多标记学习(Multi-Instance Multi-label Learning,MIML)由 Zhou 提出[4],提出后产生了很大的影响,作为一种新颖的机器学习框架得到了很好的发展,如今整个多示例多标记学习的生态已经日益繁荣[4-7]。
传统的监督学习使用一个示例(instance)来描述一个对象(object),这里的示例亦即一个特征向量,同时使用一个类别标记(label)与此对象对应。令X表示示例空间(或特征空间),Y表示类别标记的集合,传统监督学习的任务是从给定数据集{(x1,y1),(x2,y2),…,( )xm,ym}中学习函数f:X→Y,其中xi∈X是一个实例,yi∈Y是xi的已知标记。
这种传统的监督学习框架适用于一些问题,但有很多现实世界的问题不适合这个框架。它的缺点在于每个对象只属于一个概念,相应的示例只对应于单个的类别标记。然而大多数现实世界的对象并非这样简单,可能同时对应于多个的类别标记。于是,多实例多标签学习框架应运而生,在此框架中,一个对象由多个示例描述,与多个类别标记相关联。对比上述传统的监督学习,MIML框架对于表示复杂的现实世界对象更方便自然。文献[4]中提出,多示例多标记学习使用多个特征向量来描述一个对象,得到多个示例,同时,使用多个类别标记来与此对象对应。形式上设X表示示例空间,Y表示类别标记的集合。在形式上,多示例多标记学习任务被定义为[4]:从给定数据集中学习函数f:2X→2Y,其中Xi⊆X是一组示例 {xi1,xi2,…,xi,ni}的集合,xij∈X(j=1,2,…,ni),Yi⊆Y是一组标记{yi1,yi2,…,yi,li}的集合,yik∈Y(k=1,2,…,li)。这里ni表示Xi中的示例数量,li表示Yi中的标签数量。
文献[4]基于MIML框架提出了多种MIML算法,MIMLNN(Multi-Instance Multi-Label Neural Network)是其中一种较优秀的算法。下面简要概述MIMLNN算法的主要思想和过程,并使用伪代码进行描述。
首先,收集每个MIML示例(Xu,Yu)(u=1,2,…,m)中的Xu并将其放入数据集Γ中。然后,对Γ使用k-Me⁃doids算法[8]聚类。由于Γ中的每个数据项,即Xu,是一个未标记的多示例包而不是单个示例,因此基于最大豪斯道夫距离[4]对含有每个标记的训练样本进行k-Medoids聚类,并保留每个聚类簇的中心点。
在数学中,豪斯道夫距离(Hausdorff Distance),也称为Pompeiu-Hausdorff距离。常被用于计算机视觉等领域。这个距离最早是由豪斯多夫在他1919年首次出版的书《人民报》中提出的。简单来说,如果一个集合中的每个点都接近另一个集合的某个点,那么两个集合在Hausdorff距离上是接近的。
对于两个示例的包(bag),A={a1,a2,…,ani},B={b1,b2,…,bnj},两者间的最大豪斯道夫距离为:
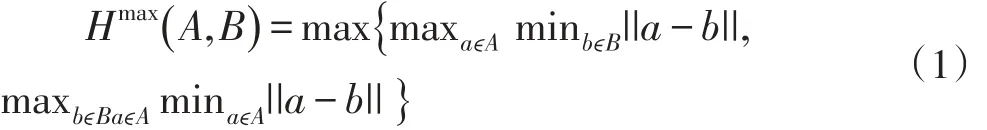
式中|.|为集合的元素数目,||.||为示例之间的欧氏距离(Euclidean Distance)。
在聚类过程之后,数据集Γ被划分为k个分区,其中中心点(Medoids)为Mt(t=1,2,…,k)。根据这些中心点,原始的多实例Xu被转换成k维数值向量zu,其中zu的第i(i=1,2,…,k)分量是Xu和Mi之间的最大豪斯道夫距离,即Hmax(Xu,Mi)。因此,最初的MIML例子(Xu,Yu)(u=1,2,…,m)已经被转化为多标签的例子(zu,Yu)(u=1,2,…,m)。然后,从数据集中学习多标签学习函数fMLL,因为 ,故可以得到所需的MIML函数。在MIMLNN算法中,使用反向传播(Back Propagation,BP)神经网络来实现fMLL。
2 数据提取和处理
蛋白质数据从世界上主流的蛋白质序列数据库UniProtKB取得。UniProtKB分为Swiss-Prot和TrEM⁃BL两个子数据库,Swiss-Prot的注释经过人工手动完成并复核,本文选用Swiss-Prot中的数据进行训练和验证,这样得到的结果更有说服力。
使用关键词检索,从Swiss-Prot获得了153条玉米蛋白质数据,每条玉米蛋白质数据,均包含两个部分:蛋白质结构域(Domain)序列数据和基因本体(Gene Ontology,GO)编号表示的分子功能(Molecular Function)数据。
蛋白质结构域是给定蛋白质序列和蛋白质(三级)结构的保留部分,它可以独立于蛋白质链的其余部分进化、作用和存在。每个结构域形成一个紧凑的三维结构,往往可以独立稳定和折叠。大多数蛋白质由不止一个结构域组成,同样的一个结构域可能出现在各种不同的蛋白质中。分子进化使用结构域作为基本的结构单元,这些结构可以以不同的排列进行重组,以创建具有不同功能的蛋白质。结构域长度从约25个氨基酸到500个氨基酸长度不等。此概念最早由Wet⁃laufer在1973年提出[9]。Wetlaufer将结构域定义为蛋白质结构的稳定单位,可以自动折叠。大自然通常将几个结构域结合在一起形成具有多种可能性的多域和多功能蛋白质。在多域蛋白质中,每个结构域都可以独立地完成自己的功能,或者以与其邻居一致的方式完成它自己的功能。
她一一向我介绍她的家具:懒人沙发,逍遥椅,水晶吊灯和银台灯。并说,老同学喜欢什么就搬走什么,没有问题。
基因本体论(GO)是一项重要的生物信息学计划。在生物学领域没有通用的标准术语,术语用法可能特定于物种、研究领域甚至特定的研究小组而异,而此计划旨在解决这些混乱的表示方法。简单来说,GO提供了一种统一的编号方法来表示所有物种中基因和基因产物的属性,它涵盖三个领域:细胞成分、分子功能、生物过程,本文中我们使用GO分子功能的编号来表示蛋白质的功能。
GO本体文件可以从GO网站以各种格式免费获得。表1展示了一个编号为GO:0000005的用来描述某种分子功能的GO条目。

表1 GO本体示例
使用文献[10]中提出的基于Conjoint Triad法[11]的氨基酸序列特征向量提取方法,对上述每个条目中的结构域进行特征向量的提取,每个结构域得到对应的一个特征向量,即为一个“示例”。同时,每个GO编号则对应的作为一个“标记”。以这种逻辑关系得到一个完整的玉米多实例多标记样本库,导入MIMLNN算法中进行训练,并进行功能预测。
3 结果与对比
使用3种主流的多标记学习评价指标对结果进行评价。
Hamming Loss指标[12-13]用来评价所得结果与实际情况之间的差异大小,也就是样本实际上拥有标记Yi,却没有被成功预测,或者,实际上没有拥有标记Yi,但是被误认为拥有的可能性,其值越小则预测效果越好。定义如下:
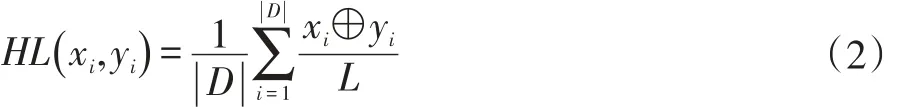
式中|D|为样本数量,|L|为标记数量,xi为预测值,yi为真实值。
maF1、miF1 指标[14-15]分别对 F1 值(F1 Measure)应用宏平均(macro average)和微平均(micro average)。

式中|D|为样本数量,|L|为标记数量,xi为预测值,yi为真实值,yi,l为yi的第l个元素。
miF1先对所有示例和标记直接进行平均。其计算方法如下:
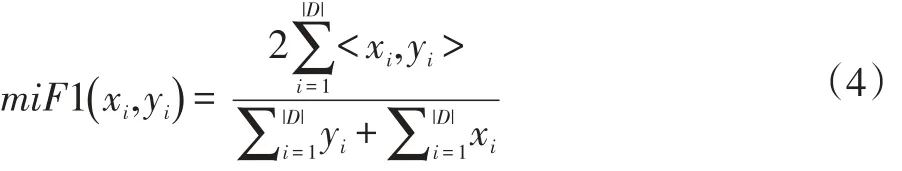
式中|D|为样本数量,|L|为标记数量,xi为预测值,yi为真实值,<·>为数量积。
使用第2节处理得到的玉米蛋白质数据,使用MIMLNN算法在最优参数条件下进行蛋白质功能预测,使用上述三种主流的评价标准进行评价,结果如表2所示,一共进行10次预测实验,采用10折交叉验证(保留3位小数)得到,在表的末尾列出了10次实验结果的平均值以及方差。如上文所述,Hamming Loss的值越小越好,其余两者反之。
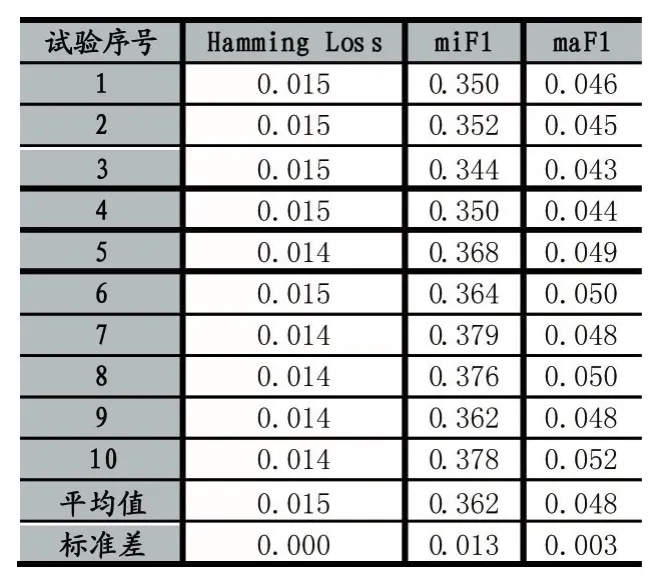
表2 三种指标下玉米蛋白质功能预测结果
表3中展示了本文得出的结果和文献[16]中对于两种微生物的蛋白质功能预测的结果对比,表中数据均以平均值±标准差的形式给出。
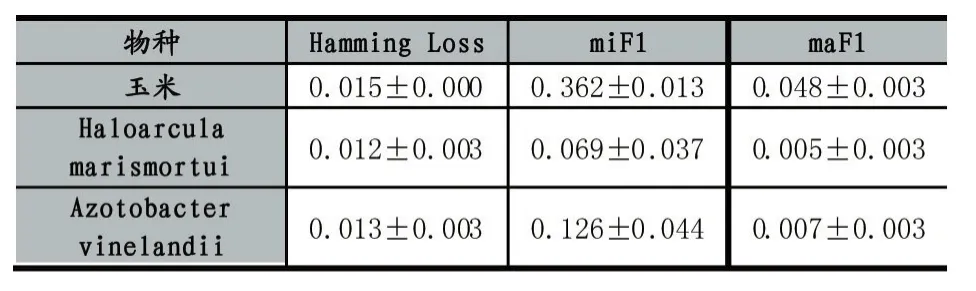
表3 与同类预测结果的对比
可见,在Hamming Loss指标下,本文中的预测结果取得了近似同等的表现,而在其余两种指标下,本文预测结果皆显著更好。
4 结语
玉米作为重要的谷物之一,对其蛋白质进行预测具有显而易见的现实意义。本文应用了一种优秀的多示例多标记学习算法MIMLNN进行玉米的蛋白质功能预测,通过对比,证明取得了良好的结果,因此具有一定的实用价值。同时,在机器学习技术日新月异的今天,这类方法仍有较大的改进空间以提高预测效果。
