基于构象相似度的多目标粒子群算法

朱榜

（上海海事大学信息工程学院，上海 201306）

0 引言

蛋白质是由20种不同氨基酸组成的生物大分子，其在生物细胞中扮演着许多重要角色，例如酶的活性、物质的储存和运输、信号转导、抗体等[1]。而蛋白质的功能与其三维结构是直接相关的，因此预测蛋白质的三维结构对于研究蛋白质的功能和作用有非常重要的意义。理论计算方法（也称热力学方法）是一种常用的蛋白质结构预测方法，由于它仅利用一级序列信息进行预测，而不需要任何其他已知蛋白质结构信息，所以，该方法也是一种较理想的预测方法[2]。理论计算方法的有效性取决于两方面：①势能函数（评估函数），该函数模拟参与蛋白质折叠过程的相互作用力，理想地将蛋白质结构排列为全局最小值；②有效的搜索算法，能够处理具有大量不可行构象的多维构象搜索空间。因此，理论蛋白质结构预测具有较高的计算成本，无法通过详尽的搜索来获得结果，一般采用元启发式算法。

当一个优化问题涉及多个目标函数，找到这些目标函数的最优解，称为多目标优化[3]。在多目标优化中，一个目标的最优解对于另一个目标可能不是最优的，因此，人们不能选择只有一个目标达到最优的解。一般来说，在一个以上相互冲突的问题中，没有一个最优解，相反，存在一组最优解，称为最优帕累托前沿。这个组合包括在不减少另一子目标的情况下不可能改进一个目标的解集。理论蛋白质结构预测问题也可以被适当地表示为多目标优化问题（MO），因为其势能函数一般有几个能量项组合而成，这些能量项在优化过程中可能存在冲突。跟以往单目标方法中直接使用加权系数对这些能量项进行耦合不同，MO方法通过将这些能量项以不同的方式组合成多个目标同时进行优化，避免了优化过程中能量项冲突导致的误差，从而能够更好地探索蛋白质构象空间。在过去几年中，已经有不少MO方法被应用到理论蛋白质结构预测中[4-7]。

粒子群算法（PSO）是基于群体协作的随机搜索算法[8]，是一种广泛应用的优化和搜索问题的元启发式算法。PSO能够同时探索搜索空间的多个区域，且能够有效地处理多模态问题。这些特征使得PSO算法在解决多目标优化问题上具有很大的优势：第一，它的高效搜索能力有利于得到多目标意义下的最优解；第二，它通过代表整个解集种群，按并行方式同时搜索多个非劣解，也即搜索到多个Pareto最优解；第三，PSO算法的通用性比较好，适合处理多种类型的目标函数和约束，并且容易与传统的优化方法结合，从而改进自身的局限性，达到更高效率的解决问题[9]。本文针对蛋白质结构预测问题，将蛋白质构象相似度引入到多目标粒子群算法中，增加帕累托前沿的多样性，从而得到最优蛋白质构象。

1 算法实现蛋白质表示及势能函数

本文采用粗粒度蛋白质模型用于降低评估特定构象能量所需的计算成本。该模型中蛋白质侧链被链接主链的第一个碳原子Cb取代，主链仅用N、C、Ca三个原子表示。每个蛋白质构象由其氨基酸序列中每个残基的主链二面角{φ，ψ，ω}集合表示。新的蛋白质构象由改变二面角φ和ψ实现，肽键角度ω在算法搜索期间不变，保持在180°。

蛋白质的势能函数表达式如下：

其中，Ebond和Eangle分别是键伸缩势能和键角弯曲能，为了减少构象空间复杂度，本文将键长键角设置为理想值，故Ebond=Eangle=0；Edih是二面角扭转势能，由简单的傅里叶级数表示；Evdw是范德华相互作用，由所有主链原子之间及主链原子与侧链原子之间的相互作用和侧链原子与侧链原子的相互作用两部分组成；Ehb是氢键相互作用，氢键由蛋白质主链上的羰基和酰胺基团形成，对于蛋白质的结构稳定性至关重要，其形成方式确定了蛋白质的二级结构（α螺旋，β-折叠和弯曲），本文使用文献[10]结合角度项的径向12-10 Lennard-Jones势表示。该势能函数的详细信息见文献[11]。

本文从多目标优化角度考虑蛋白质预测问题，故将势能函数的能量项分解成不同的目标。Edih、Evdw、Ehb分别作为一个子目标。

2 基于表型拥挤的多目标粒子群算法

2.1多目标粒子群算法

粒子群算法是受鸟类觅食这种社会行为的启发提出的，模拟鸟类觅食时个体之间自我认知和相互协作，相互交换信息来寻找最优解的一种随机优化的智能技术[12]。在PSO中，每个粒子是优化问题的一个潜在解，它跟随当前的最优粒子在解空间中飞行，从而向最优解靠近。因此每个粒子的速度和位置公式可表示为：

式中：

vi(t)和xi(t)分别为t代粒子i的速度与位置，pBesti是粒子i的个体最优位置，gBest(t)是t代所有粒子的全局最优位置，r1、r2为[0 ,1]区间上独立的随机数，ω为惯性权重，一般在（0,1）区间，c1、c2为加速系数。

为了避免算法陷入局部最优，并增加解的精确度，本文采用动态变化的惯性权重与加速系数，其公式如下：

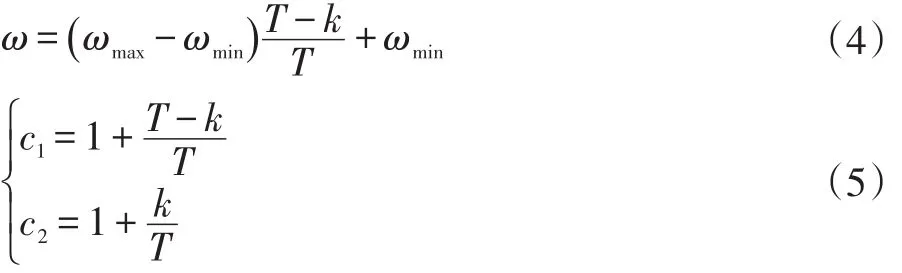
式中：ωmax和ωmin分别取0.9和0.4；T为最大迭代次数；k表示当前迭代的次数。

多目标粒子群算法与单目标粒子群算法的主要区别是多了存档和限制外部档案规模的过程，并且也不是简单地通过适应度函数的比较来求出解，而是用一组非劣解集去逼近真实的Pareto前沿[13]。算法的大致步骤如图1所示。

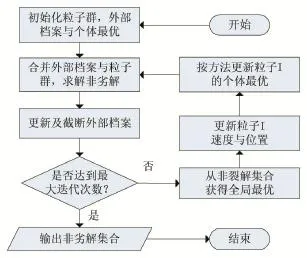
图1 多目标粒子群流程图

2.2基于擂台赛法则的非支配集求解

在多目标优化中，给定x和y两个解，如果x在所有目标中至少等于y，且至少在一个目标中x大于y，则称x支配y。Pareto最优集是由所有非支配解组成的集合。在多目标粒子群算法中，每一代外部档案由上一代外部档案与当前粒子群集合的非支配解集构成。本文采用擂台赛法则构造非支配，在每一轮比较时，从构造集中选出一个个体出任擂主（一般为当前构造集的第1个个体），由擂主与构造集中其他个体进行比较，败者被淘汰出局,胜者成为新的擂主，并继续该轮比较；一轮比较后，最后的擂主个体即为非支配个体；按照这种方法进行下一轮比较，直至构造集为空[14]。其具体算法流程如下：

算法1基于擂台塞法则的非支配集构造

2.3基于构象相似度的外部档案裁剪技术

多目标粒子群中采用外部档案来存储每一代产生的非劣解。随着迭代的进行，外部档案会逐渐膨胀，算法的计算复杂度也随之增加，对此一般通过对外部档案设置一个最大规模N，当档案中粒子数超过N时，则按照一定规则进行裁剪。目前常见的外部档案的维护策略有自适应网格法[15]、拥挤距离法[16]、k近邻法[17]等。其中，自适应网格法的基本思路是对目标空间进行网格划分，通过统计网格中的粒子数来估计粒子密度，粒子所在网格包含粒子越多则其密度越大，当外部档案中粒子数超过最大规模N时，则从密度最大的网格中随机选择粒子进行删除。

在蛋白质结构预测中，为了更广泛地搜索构象空间，维持外部档案中构象的多样性，本文引入蛋白质构象相似度来裁剪外部档案。蛋白质构象相似度使用疏水性残基Ca位置的距离矩阵误差（DME）表示，其计算公式如下：

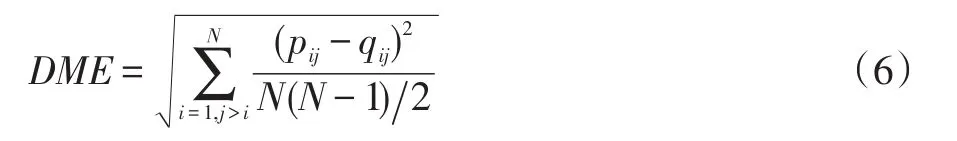
其中pij和qij分别是蛋白质p、q疏水性残基i、j的Ca原子距离，N是蛋白质疏水性残基的个数。

基于蛋白质构象相似度的外部档案裁剪技术具体步骤如下：

Step 1：选择密度最大的网格Gi，随机选择该网格中的一个粒子j，并根据式（6）计算该粒子j与Gi中其他粒子的DME值；

Step 2：删除Gi中除粒子j以外，DME值最小的粒子，更新Gi的密度；

Step 3：如果外部档案大小小于最大规模N则算法结束，否则返回Step1。

2.4基于构象相似度的多目标粒子群算法流程

根据2.1到2.3小节，本文算法的具体流程如下：

算法2 PCMOPSO

3 结果与分析

本文算法的运行环境为搭载Intel Core i7处理器，8GB运行内存的64位Windows10操作系统。算法参数设置为：最大迭代次数T=1000，外部档案大小N=100，种群大小M=100，算法独立运行30次。

算法测试数据为 2rlg、1vii、2p81、2jzq、1xzy、2evq、1e0l、2dmv、1k36、1fna、2kp0、1crn、1e0g、2hbb、2gb1 等15条长度不等，具有不同二级结构的天然蛋白质，这些蛋白质的天然结构已由实验等方法测得，其相关数据从PDB数据库下载得到。

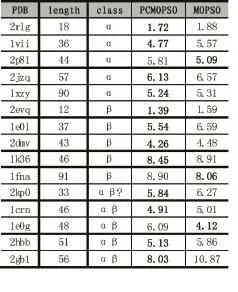
表1 蛋白质信息及其测试结果

为了评估预测得到蛋白质构象的质量，本文采用与蛋白质天然结构的均方根偏差（RMSD）作为预测构象的度量。RMSD的值越低，则预测构象越接近天然结构，因此在多目标方法中，本文选取外部档案中RMSD值最小的粒子作为该蛋白质的预测构象。本文所有RMSD的计算中只考虑氨基酸的骨架原子。表1给出了本文算法PCMOPSO与MOPSO算法针对15种蛋白质的RMSD值，其中，MOPSO外部档案维护策略为拥挤距离法，其他速度位置更新等配置与PCMOPSO相同。从表1中可看出基于表型拥挤的多目标粒子算法所得结果明显优于MOPSO，80%（12条）的蛋白质都得到了优化。其中1vii的RMSD得到0.8Å的改善，1eol得到1.05Å的改善，2hbb得到0.73Å的改善，2gb1更是得到了2.84Å的改善。测试结果表明采用构象相似度策略的多目标粒子群算法能够更好的搜索蛋白质构象空间，从而找到更接近天然结构的蛋白质构象。

4 结语

本文提出了一种基于构象相似度的构象搜索算法，其采用擂台赛法则提高获得非劣解集的性能，并引入构象相似度对外部档案集进行维护，提高Pareto前沿的多样性与均匀性，利用搜索效率高，全局搜索能量强的多目标粒子群算法对蛋白质构象空间进行多目标优化。实验结果表明，相比普通多目标粒子群算法在蛋白质结构预测中的应用，加入构象相似度策略能够更好地维持外部档案中构象的多样性与均匀性，从而获得较好的蛋白质预测构象。