数学建模下的高中数学函数教学探讨
2018-10-21杨帆湖南省怀化市新晃一中419200
杨帆 湖南省怀化市新晃一中 419200
运用数学建模解决高中函数,将数学建模方式纳入到函数教学设计中,是一个把实际问题进行抽象,化繁为简,用数学语言描述问题,进而建立数学模型,解决问题的过程.
一、数学建模是函数教学中的应用
按照新课程对高中函数的要求,是要掌握基本概念和理论知识,并且解决相关应用问题,如,分段函数、二次函数和三角函数.另外要学会将函数和实际相结合,通过函数模型解决现实生活问题,同时建立函数和其他数学知识的联系.
因此在高中函数教学课堂中教师要根据课程要求,对函数教学进行相应的改进和完善,从实践角度对函数教学进行不断优化和革新.
使用数学建模进行高中函数教学就是其中一种比较实用的方法,用建模解决高中函数问题,主要途径包括利用基本函数模型解决复合函数模型,通过现实背景抽象函数模型,利用换元解决数形结合问题等.利用数学建模进行教学设计还能有效提升教学效率,提升课堂授课质量,更新师生教学观念,满足新课程下的课堂教学需求,同时综合提高学生的创新能力和应用能力.
二、数学建模下的高中函数教学设计具体内容
(一)根据现实生活情境构建函数模型
函数是描述变量之间的一种数学模型,在解决相关应用问题时,利用数学建模,把实际生活情境抽象化,掌握基本的函数模型,利用数学建模方法的基本步骤解决实际问题.而二次函数的实际应用是比较常见的,其描述的是两个变量的关系,在现实生活中主要是结合图形解决面积、产量等问题.
例一、某商场购进一批玩具,每个20元,每天销量是100个,后因为购进成本提升,要对店内玩具进行提价,经过调查发现每提价2元,则日销量减少10个,如果不考虑其他因素,那么要想使每天的销售额达到最高,则玩具的价格应当是多少元?
分析:在实际生活中这类问题是很常见的,而用数学思维来思考,这道题考察的是销售总额和单价的函数关系.那么在课堂授课过程中,教师可以引导学生进行分析,将这类实际应用题抽象为数学函数模型.
模型构建:该题可以构建二次函数模型.假设玩具价格为x元,销售总额为y元.
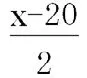
X10)=-5(x-40)2+8000
根据二次函数图象与性质可得当x=40时,销售额最高,最高收入为8000元.
例二、将生活实际情境抽象为对数函数
对数函数的应用集中体现在放射性物质,银行利息和细胞分类等方面.
如,要确定古莲子的年份,需要用到某种放射性物质,已知动植物死亡后,这种放射性物质就不再生产,原有的物质也会自动衰退,经过5730年,原有的放射性物质会衰退到原始量的一半,根据科学家的测量,古莲子的原始放射性物质含量为m,经过x年后剩余量m1与m的关系满足:m1=m.e
假设从古莲子中检测剩余的放射性物质为原始量的87.9%,那么古莲子的年份为多少年?
分析:这是一道和考古有关的现实生活情境问题,关于探求古莲子年份类的题目是十分常见的,在解决这类题的时候要善于分析,教师可以用对数函数的相关概念将这类题目抽象化,通过数学思维和语言来描述这类题,利用对数函数的相关理论知识来分析和解题.
模型构建:对数函数
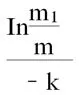
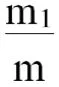
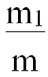
(二)构建数学模型,换元法解决复合函数
换元法是高中数学中常用的解题方法,在将数学建模纳入到高中函数教学中的时候可以将换元法和建模结合起来,尤其是面对复合函数问题,可以将复合函数简化为简单函数.教师在讲解此类问题时,首先要分析复合函数由哪几种简单函数组成,然后对其中一种函数进行换元,构造成简单函数.
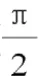
分析:这类题从表面上分析是一道常见的三角函数题,利用三角函数的二倍角公式和诱导公式,可以将函数简化为:
f(x)= -2sin2x+6sinx+1;
模型构建:可以看出这个函数的变量是三角函数,但形式是二次函数,因此这是一道二次函数和三角函数结合的复合函数,在解题过程中采用换元法,将三角函数转化为二次函数形式;
令t=sinx,可得f(x)= -2t2+6t+1,其中t∈[-1,1];
利用二次函数的解题模型,考虑定义域的求值范围,可得:
当t=1.5时,f(x)最大,最大值为5.5;
因为t∈[-1,1];因此当t=1时,f(x)最大,最大值为5.
三、教学反思
笔者在课堂教学中一般采用自主教学法,给学生充分的时间进行讨论,首先教师会进行系统讲解,每类函数问题应该怎么构建数学建模,然后让学生进行讨论,并总结出有关函数应用题的具体解决方法,从而培养出他们在实际解题过程中举一反三的能力.
总之,在数学建模下对高中函数教学进行教学设计,需要培养学生的建模意识,了解建模理论,并且不断深化学生对相关函数知识的理解程度,在课堂教学中采用"探究-讨论"的教学方法,更好地推动函数教学中的建模教学模式.
