论导数在高中数学中重要作用

张玲 巴中市恩阳区恩阳中学 四川巴中 636063

一、导数在不等式中的应用

不等式是高中数学的一个难点，而导数在不等式的证明中起着有较大的作用。有些不等式看起来很复杂，我们可以利用导数就可以让其简单化。利用导数解决不等式证明问题，通常是利用了不等式与函数的关系，构造函数，通过导数运算判断其单调性，从而将不等式问题转化为函数问题。

分析：此题目非常简洁，但很多同学无从下手，一头雾水，但若能想到把不等式问题转化为函数问题，利用导数去解决将会事半功倍。

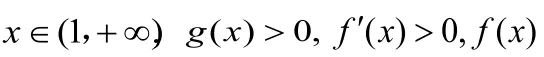
二、导数在函数中的应用举例

函数在高中数学中起着至关重要的作用，而函数最值问题又是重中之重。而函数的最值、极值、单调性等问题可以利用我们所熟悉的导数来解决。可以说有了导数，函数问题就没有那么神秘，那么深不可测了。在利用导数解决最值和极值问题时应注意他们的区别，极值不是最值，不能混为一谈。

本题主要考查的是利用导数的知识来解决函数的最值问题，利用导数求最值的一般步骤为

先判断函数的单调性，再结合该函数的单调性来确定其最大值或者最小值。

三、导数在方程解的个数中的应用

导数对于解决高次方程的根和近似值有相当主要的作用，此时如果利用常规方法来解决可能出现解不出来根、运算量大等问题，有了导数，可以降低运算量以及其难度。

本题实际解决的是函数零点问题，函数有零点等价于所对应的方程有解。因此可以利用函数零点来解决方程的根。

四、导数在实际问题中的应用

我们不能脱离实际去学数学，数学是解决实际问题的一种工具，实际应用中很多最优化问题我们都可以用导数的知识来解决。近年来的高考更加倾向于对实际问题的考查，时常在生活中会遇到利润最大，材料最省，效率更高等最优化问题，一般情况这些问题都可以用导数求最值的方法来解决。

分析：利润L等于收入R减去成本C，而收入R等于产量乘价格．由此可得出利润L与产量q的函数关系式，再用导数求最大利润．

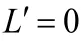
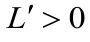
五、结语

本文归纳总结出利用导数解决中学数学问题的若干类型，结合相应的类型给出了例题，并且在一定程度上对在用导数解题时需注意和易错点给予了说明，从而方便导数初学者便于查找，在学习导数的初级阶段能够有更多的资料进行学习借鉴，在利用导数解题时注意到自己平时忽略到的方面。