基于单纯形法的磨机给料控制的研究与设计
2018-10-20刘振东王建民邓展
刘振东,王建民,邓展
(华北理工大学电气工程学院,河北 唐山 063210)
在磨矿分级过程中,球磨机的磨矿是选矿生产过程中的关键环节,磨机运行过程的控制直接影响了选矿的产量、能耗和效益[1]。对磨机运行过程的控制其实质也是对磨机给料进行控制,合理的给料量控制能够维持磨机负荷的稳定,而磨机负荷的稳定是磨机稳定运行的条件。在磨机运行过程中最关键的参数是磨机负荷,它包括给料量,给水量和钢球量。而且磨机负荷极易受其他因素的影响而发生变化,例如矿石的耐磨性、粒度、钢球的损耗和磨机衬板的磨损都会造成磨机负荷的变化,从而导致磨矿过程不稳定,使磨机经常会出现“欠磨”或“饱磨”不稳定的运行状况,使得磨矿效率和产品的质量发生较大的波动[2]。因此,合理的控制磨机的给料量对维持磨机稳定运行至关重要。为了满足磨机稳定的运行要求,近年来不少学者提出了各种关于磨机给料的智能优化方法。其中较为突出的有以下三种:一是模糊控制方式的磨机给料控制系统的设计[3]。这种方法能够克服非线性因素以及噪声带来的问题,但是其对信息的简单模糊化处理的精度不高,系统的稳态误差很难消除;二是利用模型预估未来输出偏差的预测控制方法[4-5]。这种方法能够很好的克服系统的大惯性、大滞后特性,但是很难精确地获取预测传递函数;三是自动寻优方式下的自寻优控制磨机给料量[6]。这种控制方法可以保证系统始终工作在最佳区域,实时跟踪工况的变化以调节控制参数,但是,实时控制要求高,参数调节频繁,不利于系统的稳定运行。
针对磨机运行过程中的非线性、大惯性、强耦合、大时滞、随机干扰大等特征,以及磨机运行状态和磨机负荷的检测、控制属于“黑箱”问题,常规的PID控制器的控制效果不是很理想[7]。于是本文根据选矿工艺的实际工作过程,提出了一种基于单纯形法的PID智能控制器的设计方法,利用单纯形算法的寻优过程,实时的进行PID控制器的三个参数调整,使PID控制器工作处于最佳的调节状态,以实现稳定的给矿。提高控制器的自适应能力,让其能够更好的抵抗外界的干扰,最终实现提高磨机工作效率的同时降低各种损耗的功能。仿真实验结果表明了该方法的优越性、合理性和科学性。
1 球磨机系统的运行特性
磨机的动态运行特性非常复杂,会受到诸多因素的干扰,所以其最佳工作点常常会随着不同的参数变化而发生漂移的现象[8]。磨机的工作特性如图1所示,可以看出磨机负荷与磨机的功率、磨音和磨机的出力随时间的变化关系,其变化都是呈现非线性的关系,但是三者的变化中都存在各自的极值。
其中S表示磨音特性变化曲线,P表示功率特性变化曲线,F表示出力特性变化曲线。由于磨机的功率、磨音和磨机出力随时间的变化并不是同步的,因此将磨机的特性曲线分成三部分。t1和t2将整个磨机运行特性划分为Ⅰ、Ⅱ、Ⅲ三个区间。其中t1和t2分别对应最大功率和最大出力。控制的目标就是为了让磨机工作在第二部分,也即是Ⅱ区。在第二部分区域,可以看到,功率呈下降趋势,磨音信号基本保持不变,曲线变得非常平缓,而磨机的出力会继续上升直至达到最大点。在此区域内,磨音基本保持不变,磨机内的料量达到恒定,磨机的功率消耗不是很大,而磨机的出力达到了最大[9],磨机能够在较大的工作效率下保持稳定的运行,因此区域是磨机工作运行的最佳运行区域。我们的目标是通过各种方法进行调整使磨机运行在此区域内[10]。而其他两个区域都不能保证磨机的稳定运行,在实际调整中应当避免。
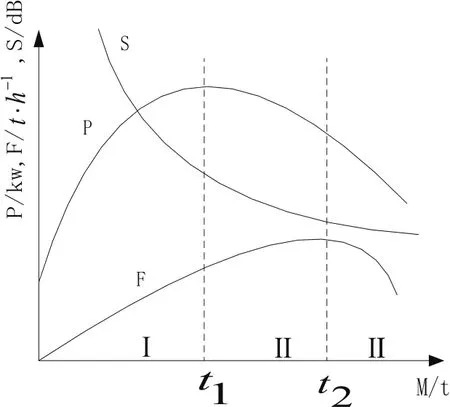
图1 磨机运行特性曲线Fig.1 Mill running characteristic curve
2 单纯形法的磨机给料优化控制系统
2.1 单纯形法的基本原理
单纯形算法是最常见的用于模式优化的算法之一,其特征在于直接搜索而不需要计算梯度。单纯形法是通过将单纯形的各个顶点的目标函数值计算出来,在搜索区间内,根据单纯形法的规则进行寻优搜索,最后比较单纯形各个顶点的目标函数值大小,来判断目标函数值的变化情况,从而确定合适有利的搜索方向和步长[11-12]。
在n维空间中,单纯形是一种多胞体,它的n+1个顶点不是在同一个超平面上。正规单纯形即是所有棱长都相等的单纯形。是某一单纯形的n+1个顶点的位置向量。对于给定的初始点和正数h,按下面公式来整定的单纯形是以为顶点h为棱长的正规单纯形:
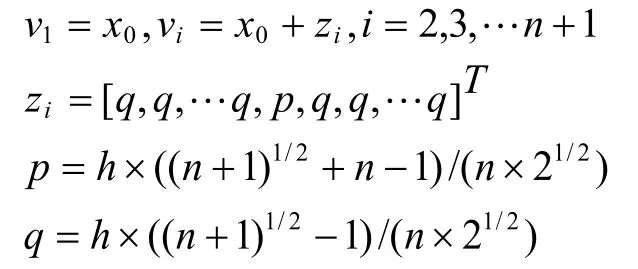
单纯形法的基本思想就是通过选取初始出发点,来构造初始单纯形[13-14]。从初始时刻的状态出发,进行迭代寻优。每次进行迭代的目的就是通过单纯形法的寻优过程寻找新的最优单纯形,使得目标函数值逐渐的向极小值趋近,直到搜索到最小点。单纯形法是通过反射、延伸、收缩和减小步长四种操作完成寻优过程。

2)延伸:按下面的公式进行计算:

3)收缩:压缩过程比较复杂,需要分以下几种情况进行处理:

若不成立,按如下公式进行计算压缩点:

4)减小棱长:原单纯形的最好顶点vl维持不变,各棱长缩短一半。计算公式为:
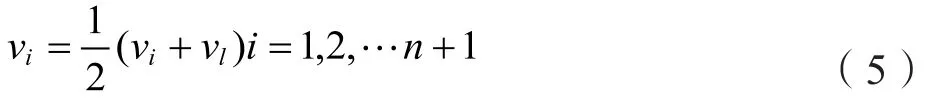
5)终止准则:计算

2.2 单纯形法的优化过程
单纯形算法就是依靠这几种操作方式进行寻优的,通过比较每个顶点的目标函数值的大小,判断各个顶点的特征。最好点保留,最差点进行各种操作,首先按(1)式进行反射操作,通过反射如果有则可以得到比更好的点。如果出,说明通过反射之后的点更小了,前进的步长不够,沿着的方向还需要向前延伸,按(2)式进行延伸操作;若是延伸之后仍有那么就用代替 ,其它的n个顶点保持不变,重新组成新的单纯形。若是反射之后不满足,即反射点 并不比原单纯型 的最好顶点好,说明最坏点反射时前进的步长太大,此时需要进行步长压缩处理操作。若也即是反射之后的点比原单纯形最坏的点还要坏,反射的步长太大,舍弃,压缩向量 ,按(3)式来进行压缩操作;压缩后需要进行判别是否满足。若是满足,则对压缩点进行舍弃,从而转向减小棱长的计算,按(5)式进行操作,不然用 替换 从新组成新的单纯形,转入5)。若满足,则按(4)式进行压缩操作,压缩后比较一下压缩点 是否比反射点 还坏,即。若成立,舍弃压缩点,转向棱长减小操作,按(5)式进行操作;若不成立,用 代替 从新组成新的单纯形,再转入5)。通过这样的一个过程将会得到最优的结果。
2.3 单纯形法优化PID控制器的结构
2.3.1 磨机给料控制系统的设计
根据磨矿分级过程中磨机给料控制的特性和控制要求的分析,本文利用串级控制回路进行给料控制,如图2所示。主回路利用智能控制算法实现给料量的设定,而副回路利用单纯形优化算法进行PID参数的调整,从而实现稳定的给料。在主回路中,通过磨音来间接的设定给料量的大小。副回路控制是通过主回路中智能算法确定的给料量设定值来进行闭环控制给料量的。通过这样的串级控制能够确保磨机的稳定运行,从而提高磨机的工作效率。通过给矿控制算法来控制给料机的给料速度,以实现磨机给料按设定值进行变化。本文中重点介绍磨机的给矿控制算法机理。
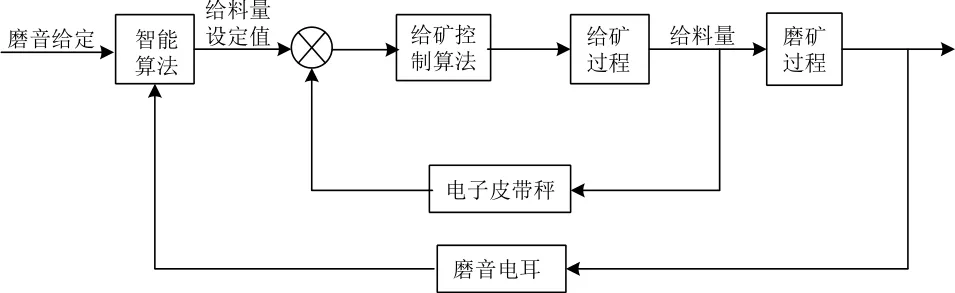
图2 磨机控制系统原理图Fig.2 Schematic diagram of mill control system
2.3.2 优化的PID控制器的结构设计
单纯形法的PID控制器参数的优化就是利用单纯形法的寻优过程来进行PID参数实时调整。在每一个采样时刻,根据输入量r与输出量y的偏差e=r-y在本文中结合实际工艺偏差量为给定量与检测量之间的误差。利用单纯形法的操作过程,来整定优化PID控制器的参数,使其我们选取的目标函数值有最小值。设计的单纯形算法的PID控制器优化的结构图[15]如图3所示。
2.4 PID控制器参数的优化设计
(1)目标函数的选取。为了满足系统性能的需求,本文给出某种形式下的目标函数,选用如下的二次函数作为目标函数:
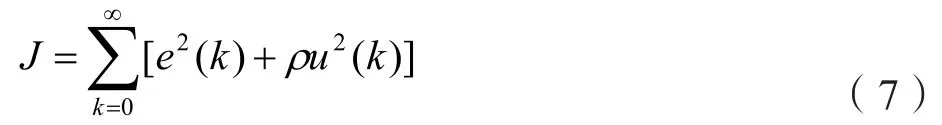

(2)PID参数寻优过程。利用单纯形算法进行PID参数的整定优化过程的流程图如图4所示。
Step1:通过Z-N法整定确定PID参数Kp、将其作为单纯刑法的初始顶点值。
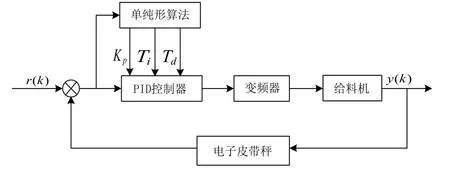
图3 基于单纯形算法优化的PID控制器参数结构图Fig.3 Parameter structure of PID controller based on simplex algorithm optimization
Step2:选择合适的参数构造初始的正规单纯形。
Step3:利用单纯形法的四种寻优操作方式进行最佳参数寻优。
Step4:计算目标函数值的大小。
Step5:比较目标函数值,判断是否找到最优值,如果找到转入下一步,如果没有找到转到第三步。
Step6:输出优化后的参数。
Step7:停止。
3 运行效果与仿真结果分析
3.1 运行效果分析
(1)生产管理层,也即是在厂内办公室里,经由以太网完成通信,厂内领导可以对现场的设备运行情况进行实时观察。
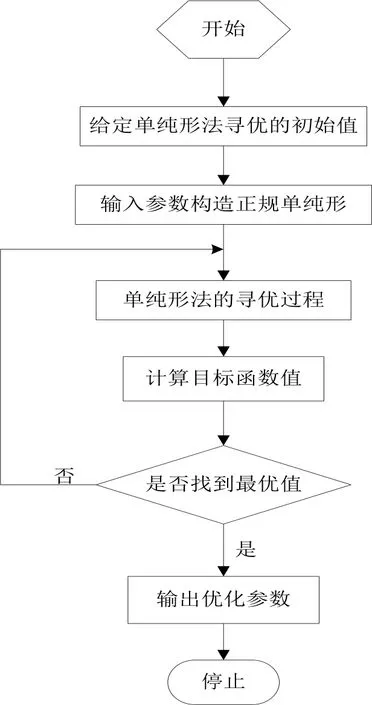
图4 PID参数寻优流程图Fig.4 PID parameter optimization flow chart
(2)监控操作层,监控计算机与磨机控制柜进行通信完成数据的传输,文中磨机控制仪是由实验室自主研发的,监控组态界面由C#应用程序设计,操作人员在监控室内实时的监视和操作现场的运行情况。以便及时的调整生产,同时记录数据以便日后的数据分析和利用。将单纯形优化算法嵌入到C#应用程序设计的监控系统中,通过对过程控制层的数据分析和运算来指导给矿量的调整以及优化PID控制参数,从而达到磨机给矿量的最优控制。
(3)过程控制层,磨机控制柜与现场的设备进行连接,接收操作层的指令对现场设备进行控制,并且将采集到的现场设备数据在监控计算机上进行显示。
通过工控计算机与磨机控制仪之间的实时通信和数据传输,来对磨机给料量进行实时的监控,实现人机交互。将该优化的方法应用在河北承德某选矿厂,并投入试运行,运行效果如图6所示,曲线1表示料的运行曲线,曲线2表示磨机负荷运行曲线,运行效果较好,基本满足工艺要求。试运行情况表明,该方法提高了磨机的台时处理量,在原有的方法基础上磨机处理量提高了6%,同时也减少了磨机出现“饱磨”或“欠磨”的次数,降低了磨机故障的概率,大大提高了磨机的工作效率。
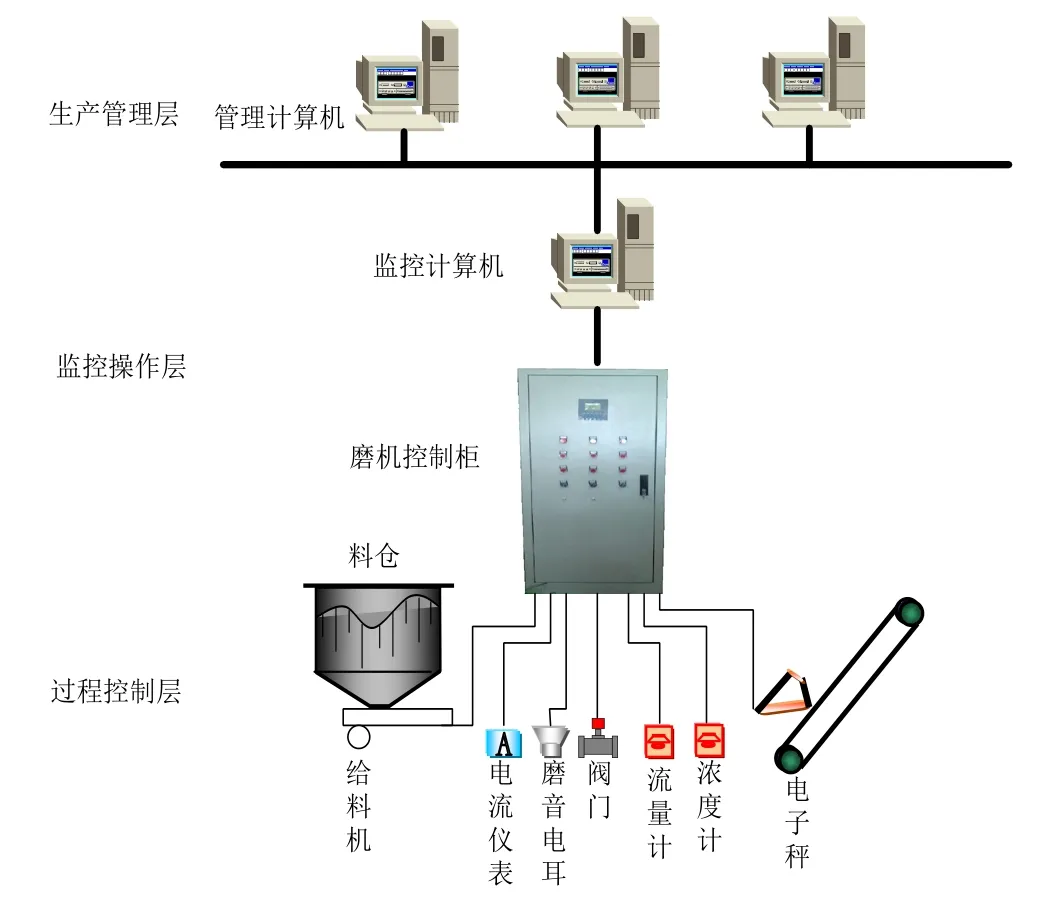
图5 选矿厂磨机控制系统结构图Fig.5 Design of mill control system for concentrator
3.2 仿真研究分析
为了进一步的验证该方法的优越性,将本文设计的单纯形算法优化的PID控制器用在磨机的给矿量控制上。因为磨矿过程特性非常复杂,大惯性、滞后性、时变性等特征影响较大。因此用二阶系统近似的替代磨机给料控制的传递函数
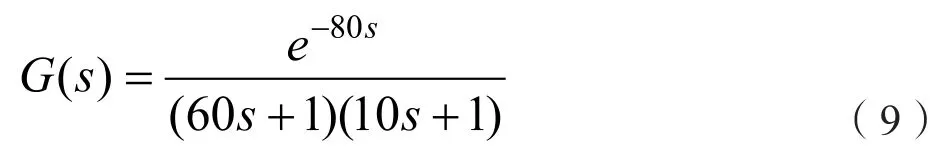

表1 两种控制方法的性能指标Table 1 Performance of two control methods
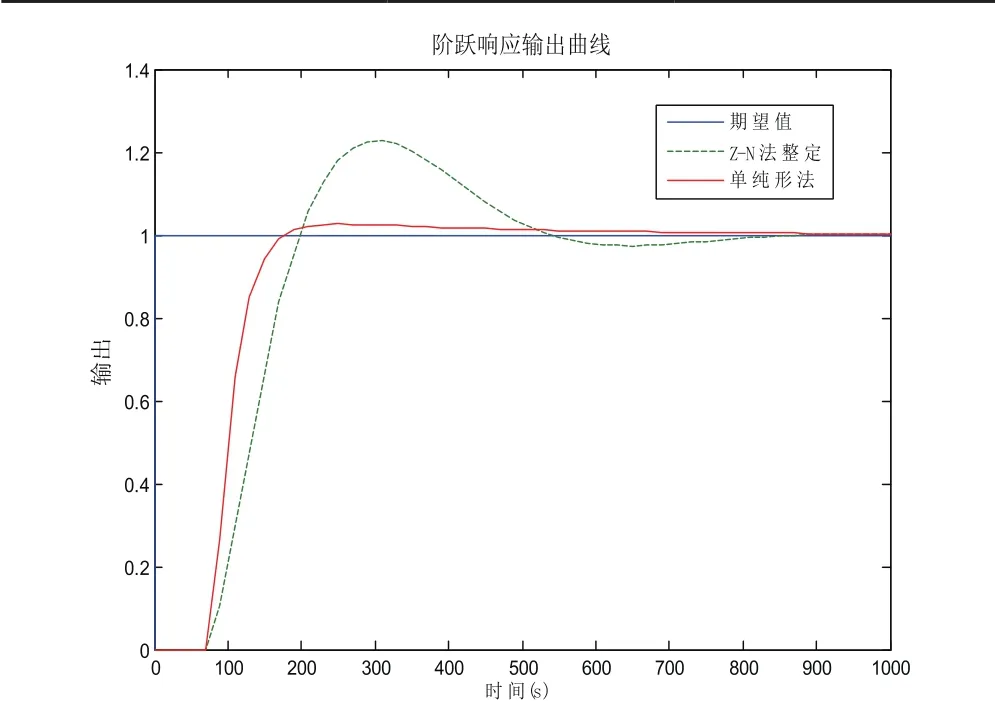
图7 优化前后系统的阶跃响应曲线Fig.7 Optimize the step response curve of the system before and after
4 结论
针对磨机运行过程的非线性、大惯性、随机干扰大等问题,本文提出了一种基于单纯形算法的PID参数整定的优化方法进行磨机给料的控制。通过单纯形寻优实时的调整PID参数从而更好的调节磨机的给料。理论分析和实际试运行效果表明,本文提出的单纯形算法优化PID控制器参数的方法,与常规的PID控制器相比较,系统的超调量减小,动态过程平稳,稳态误差较小,具有较好的鲁棒性,能够很好的抵抗外界的干扰,有效的减少磨机给料的波动。对于磨矿过程较复杂的控制系统,具有非常好的实用性。
