界面热阻对π型铸件凝固过程温度场的影响

焦壮壮，杨 燕，袁训锋，王艺儒

（商洛学院，陕西商洛 726000）

采用数值模拟技术研究铸造凝固过程能够有效的降低成本，缩短研发周期。20世纪60年代，Forsund[1]最早采用有限差分法进行铸件凝固过程的传热计算，开创了应用数值模拟技术研究铸件凝固过程的先河。随着计算机技术和数值模拟方法的发展，数值模拟在凝固过程中占据重要地位。牛晓武[2]、刘爱敏[3]、刘艳明[4]等采用有限元软件ANSYS对机床电机座和II型铸件凝固过程进行模拟，对铸件缺陷进行预测。李岩[5]、刘洋[6]、贾瑞娇等[7]采用ProCAST软件对数控镗铣床滑枕、框架铸件、铝合金轮毂温度场进行模拟计算，探讨最佳工艺过程，从而避免浇不足、冲沙、缩孔等铸造缺陷。张相华[8]将界面热阻条件等效为边界条件，通过计算积分的办法实现界面热阻条件的约束，采用算例证明方法的正确性和有效性。这些均为基于商业软件进行温度场模拟研究，无法揭示凝固过程的部分物理本质。袁训锋[9，10]、胡瑞霞[11]、杨燕[12，13]等采用直接差分法求解热传导方程，运用C++语言编写模拟程序，研究界面热阻对T型和L型铸件温度分布及拐角处凝固速率的影响。未涉及对更接近工程实际的π型铸件凝固过程研究。

本文在文献[9－10]的基础上，以镁合金π型铸件为研究对象，探讨界面热阻对π型铸件凝固过程温度分布的影响，绘制重点位置的温度随时间变化曲线。

1 铸件计算模型

1.1 π型铸件模型

π型铸件模型如图1所示，铸件模型由底座和冒口组成。铸件结构尺寸如表1所示。

1.2 参数值的选取

铸造外部条件如表2所示，材料AZ91合金和铸型的热物性参数如表3所示。

1.3 热传导微分方程

图1 π型铸件模型图

表1 π型铸件结构尺寸图（单位：cm）

表2 铸造的外部条件

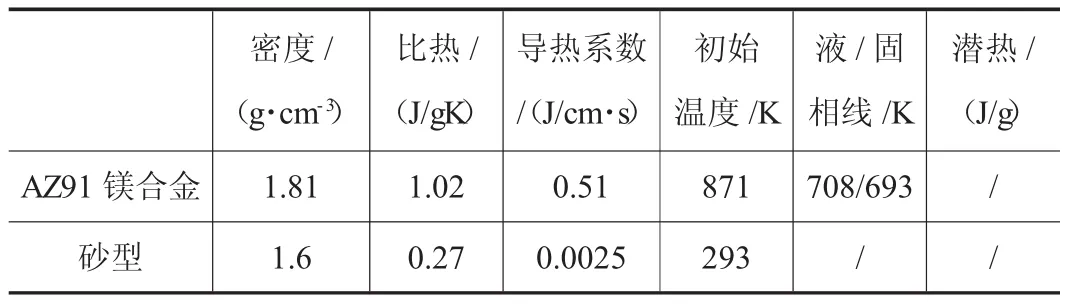
表3 热物性参数

2 温度场模拟程序的实现

2.1 网格剖分

选择82cm×82cm的正方形区域进行计算，网格大小设定为1cm×1cm，总网格数为82×82，离散化后的计算区域如图2所示。

2.2 程序实现过程

在差分单元上直接应用能量守恒定律，根据单元内积蓄的热量等于通过各面传入和传出热量的 代 数 和 ， 建 立 节 点 方 程（i，j）单元 t时刻的温度为，（i，j）单元 t+Δt时刻的温度为，Ax=Δt（/ρcpν）与材料的密度和定压热容有关，ν为单元的体积，Δt为时间步长，TNS为单位时间从各面传入单元热量的代数和。

图2 离散化计算区域示意图

在计算过程中，选取时间步长Δt=0.02s，空间步长Δx=Δy=1cm。计算获得数据采用Tecplot软件可视化处理进行定性分析，特征数据运用Origin软件绘制曲线图进行定量分析。

3 模拟分析

3.1 铸件/铸型热阻对温度分布的影响

AZ91镁合金在不同铸件/铸型热阻（h1）,凝固时间为4000s的温度分布如图3所示。从图中可以看出，铸件/铸型热阻为150s·cm2·K/J时，热量主要通过铸件/铸型界面和铸件/空气界面传输到铸型、空气中，冒口部分迅速形成明显的“梯形状”热扩散层；两冒口间铸型中部形成较小的“U形”低温区域；铸件底座部分单元格呈现红色温度较高，热量传递缓慢，凝固过程中此部分易形成封闭的液相区，最终形成缩孔、缩松等缺陷，如图3a所示。随着铸件/铸型热阻h1增大，铸件/铸型界面导热能力减弱，热量主要通过铸件/空气界面导出，铸件界面冒口部分热扩散层“梯形状”向“矩形状”转变；两冒口间铸型中部的“U形”低温区域逐渐增大，如图3b、c所示。当铸件/铸型热阻为2500s·cm2·K/J时，铸件/铸型界面导热较少，热量主要通过冒口部分向外传输，冒口部分形成“矩形状”热扩散层，整个铸件从冒口部分向内部区域凝固，如图3d所示。

图3 铸件/铸型热阻（h1）对温度分布的影响

定量分析AZ91镁合金在不同铸件/铸型热阻（h1）条件下温度分布情况，图4为选取拐角部分（i=15，j=23）和（i=27，j=23）单元绘制温度与时间变化关系曲线。从图中可以看出，AZ91镁合金在不同铸件/铸型热阻条件下，内外拐角处的温度先快速升高到极大值，随后缓慢减小趋于稳定；随着铸件/铸型热阻h1的增大，温度升高速率减慢，温度到达极大值的时间逐步增加且极大值温度逐渐减小，凝固后期不同铸件/铸型热阻外拐角部分单元格温度差异减小；在h1=150s·cm2·K/J时，内外拐角最高温度达到780.9K、801.8K，如图4a、b所示。通过观察图4c发现，凝固初期，外拐角部分与内拐角部分温度差值迅速增大，到凝固后期温度差逐渐减小；外拐角部分与内拐角部分相比更易向铸型及环境传递热量，在h1=150s·cm2·K/J条件下凝固时间达到3700s开始，外拐角温度低于内拐角温度。

3.2 铸型/空气热阻对温度分布的影响

AZ91镁合金在不同铸型/空气热阻（h2）凝固时间为4000s的温度分布，如图5所示。由图可以看出，随着铸型/空气热阻（h2）的增大，热量通过铸型/空气界面的能力减弱，底座部分热量堆积，底座部分热扩散层增厚，温度逐渐增加。

定量分析AZ91镁合金在不同铸型/空气热阻（h2）条件下温度分布情况，图6为选铸型侧面（i=1，j=16）和铸型底座（i=41，j=1）单元绘制温度与时间变化关系曲线。从图中可以看出，在不同铸型/空气热阻条件下，随着凝固时间的增加，铸型侧面和底座温度不断升高且速率逐渐增大，由于铸型侧面的厚度比底座小，热量容易在铸型底部聚集，铸型侧面温度升高比铸型底座快。铸型/空气界面热阻h2=500s·cm2·K/J，热量传输效果相对较好，铸型侧面和底座温度较低，铸型/空气热阻为 h2=5000s·cm2·K/J时，铸型 /空气界面热量传输效果较差热量富集，铸型侧面和底座温度较高。热阻介于最大值和最小值时，单元格温度介于两者之间。

图4 铸件/铸型热阻（h1）条件下温度随时间变化关系

图5 铸型/空气热阻（h2）对温度分布的影响

图6 不同铸型/空气热阻（h2）条件下温度随时间变化关系

图7 不同铸件/空气热阻(h3)对温度分布的影响

3.3 铸件/空气热阻对温度分布的影响

AZ91镁合金在不同铸件/空气热阻（h3）条件下，凝固时间为4000s时温度场分布情况，如图7所示。从图中可以看出，在铸件/空气热阻为120 s·cm2·K/J时，铸件/空气界面向外传输热量的能力强，铸件冒口附近单元格的颜色最浅，形成明显“矩形状”热扩散层，温度下降最快，优先凝固，铸件由冒口部分向底座部分凝固，如图7a所示。随着铸件/空气热阻h3的增大，铸件/空气向外传输热量的能力减弱，冒口区域优先凝固的优势减弱，“矩形状”热扩散层减少，整个铸件的高温区域面积增多，如图7b、c所示。铸件/空气热阻h3的进一步增大，“矩形状”热扩散层消失，整个铸件均为高温部分，冒口区域优先凝固的优势消失，如图7d所示。

图8 不同铸件/空气热阻(h3)条件下冒口部分（i=21，j=81）温度随时间变化关系

定量分析AZ91镁合金在不同铸件/空气热阻（h3）条件下温度分布情况，选取冒口部分（i=21，j=81）绘制温度与时间变化关系曲线，如图8所示。可以看出铸件/空气界面热阻h3=120s·cm2·K/J时，冒口部分温度急剧下降，热量传输迅速，冒口部分凝固快。铸件/空气界面热阻h3=1200s·cm2·K/J时，冒口部分温度下降缓慢，凝固速率减小，冒口优先优势减弱。热阻介于最大值与最小值时，凝固速率介于两者之间。

4 结论

（1）不同铸件/铸型热阻条件下，内外拐角处的温度先快速升高到极大值，随后缓慢减小趋于稳定。当铸件/铸型热阻为150s·cm2·K/J时，冒口部分呈现“梯形状”热扩散层，冒口之间铸型形成“U形”低温区域；随着铸件/铸型热阻的增加，冒口部分热扩散层“梯形状”向“矩形状”转变，冒口之间的“U形”低温区域逐渐增大。

（2）不同铸型/空气热阻条件下，铸型侧面的厚度比底座小，热量容易在铸型底部聚集，铸型侧面温度升高比铸型底座快。随着铸型/空气热阻的增大，底座部分热扩散层增厚，温度逐渐增加。

（3）铸件/空气热阻较小时，铸件/空气向外传输热量的能力强，冒口区域形成明显“矩形状”热扩散层，铸件由冒口部分向底座部分凝固；随着铸件/空气热阻的增大，铸件/空气向外传输热量的能力减弱，冒口区域优先凝固的优势减弱直到最终消失。