基于湿润区分层假定对Green-Ampt模型的改进

李泳霖，王仰仁，通信作者，孙小平，郑志伟



基于湿润区分层假定对Green-Ampt模型的改进

李泳霖1,2，王仰仁1,2，通信作者，孙小平3，郑志伟1,2

（1. 天津农学院 水利工程学院，天津 300384；2. 天津市节水灌溉技术与装备校企协同创新实验室，天津 300384； 3. 山西省水利水电科学研究院，太原 030012）

假定入渗过程分为前期、后期两个阶段，入渗前期土壤饱和区与非饱和区厚度之比为一常数2，非饱和区厚度随着入渗的进行而逐渐增大；入渗后期非饱和区的厚度不再随时间变化，为一定值，只有饱和区厚度随时间变化，基于此对Green-Ampt模型进行了改进。用传统Green-Ampt模型和改进模型对6组入渗测试资料进行拟合，传统模型拟合的相关系数为0.982（6组数据的平均值），相比传统模型，改进模型的拟合精度明显提高，相关系数提高了0.016，达到0.998（对应=15）；其中两组数据的效果尤为明显，相关系数分别提高了0.07和0.04，均达到了0.99以上。改进模型与传统模型同样具有较强的物理意义，但与传统模型相比，改进模型拟合得到的稳定入渗率更接近于测试值，具有更广泛的适用性。

Green-Ampt入渗模型；累计入渗量；非饱和区；入渗锋；入渗时间

Green-Ampt入渗模型是Green和Ampt在1911年提出的基于毛管理论的积水入渗模型[1]，该模型的基本假定是，入渗时存在明确的水平湿润锋面，将湿润和未湿润区域明显分开，湿润区为饱和含水率，湿润锋前即为初始含水率，即土壤水分剖面为阶梯状分布，故该模型又称活塞（或打气筒）模型[2]。由于该模型具有较强的物理意义、参数少、求解简单，从而被广泛应用。为适用不同积水条件[3-5]、不同土质土层条件、不同地形条件，研究者对模型进行了不同程度的改进。其中，刘姗姗等[6]对模型关键参数简化求解及与土壤物理参数的关系进行了研究；国外学者提出均质土壤在入渗期间从上至下依次可分为饱和层、半饱和层、湿润层和干土层[7]。Ma等[8]提出，湿润锋后土壤导水率近似用饱和导水率和饱和系数之积代替；Bouwer[9-10]建议湿润锋后导水率为饱和导水率的0.5倍；毛丽丽等[11]通过分段拟合直线方法描述含水量的分布；王文焰等[12]通过设计入渗试验测得湿润层厚度约为湿润峰后土层厚度的一半，并在此基础上假定湿润层内含水率分布为椭圆曲线，对模型进行了相应改进；彭振阳等[13]采用 Richards 模型，分析了不同入渗条件下各层厚度以及各层内含水率和导水率的变化规律，并据此规律改进 Green-Ampt 模型。本文针对传统模型拟合参数s过小甚至为负值的情况[14]，对传统模型进行改进，将入渗阶段分为前期和后期，将土壤由上至下依次分为饱和区、非饱和区和未湿润区，并结合试验数据进行验证。结果表明，改进模型的计算精度显著提高，与传统模型相比，稳定入渗率更接近实际情况。

1 基本假定与模型建立

1.1 传统Green-Ampt模型

Green-Ampt模型研究的是初始干燥的土壤在薄层积水时的入渗问题，基本假定是入渗时存在明显的水平湿润锋面，将湿润和未湿润的区域截然分开，湿润区水分为饱和含水率θ，湿润锋前为初始含水率θ。如图1。

地表积水深度记为，不随时间改变，湿润锋的位置为z，随时间前移，湿润锋处的土壤水吸力为s，该模型的主要任务是得出入渗量，入渗率及湿润锋面位置与入渗时间的关系。

由达西定律可求出入渗水量由地表进入土壤的通量，即入渗率

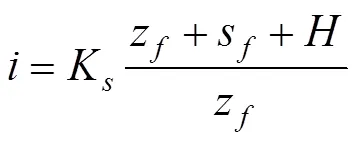
式中：K为饱和导水率，也称为稳定入渗率。

根据模型假定，由水量平衡原理，可得出累计入渗量和湿润锋z的关系：

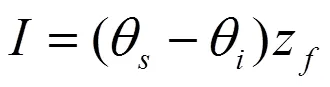
由入渗率与入渗量的关系可得：

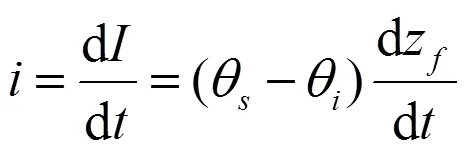
联立式（1）、式（3）可得：

对式（4）整理、积分，并利用时z=0，有：

式（1）、式（2）、式（5）便是Green-Ampt模型的主要入渗关系式。由（5）式可得z的关系，代入式（2）可得的关系：

1.2 Green-Ampt模型的改进

1.2.1 基本假定

假定入渗过程中土壤由上到下依次为饱和区、非饱和区和未湿润区，并依据非饱和区厚度的变化将整个入渗过程分为前期、后期两个阶段。

入渗前期（图2-a），非饱和区厚度随着入渗时间的增加而增加，并假定非饱和区厚度与饱和区厚度之比为一定值2，即：

式中：为一常数，Δ为非饱和区厚度，z为饱和区厚度。

入渗后期（图2-b），非饱和区厚度不再随入渗时间的增加而增加，非饱和区厚度Δ为一定值Δz。

入渗前期结束时，非饱和区厚度达到最大值Δz，此时饱和区与非饱和区依然有式（7）的关系，记此时的饱和区厚度为Δz。

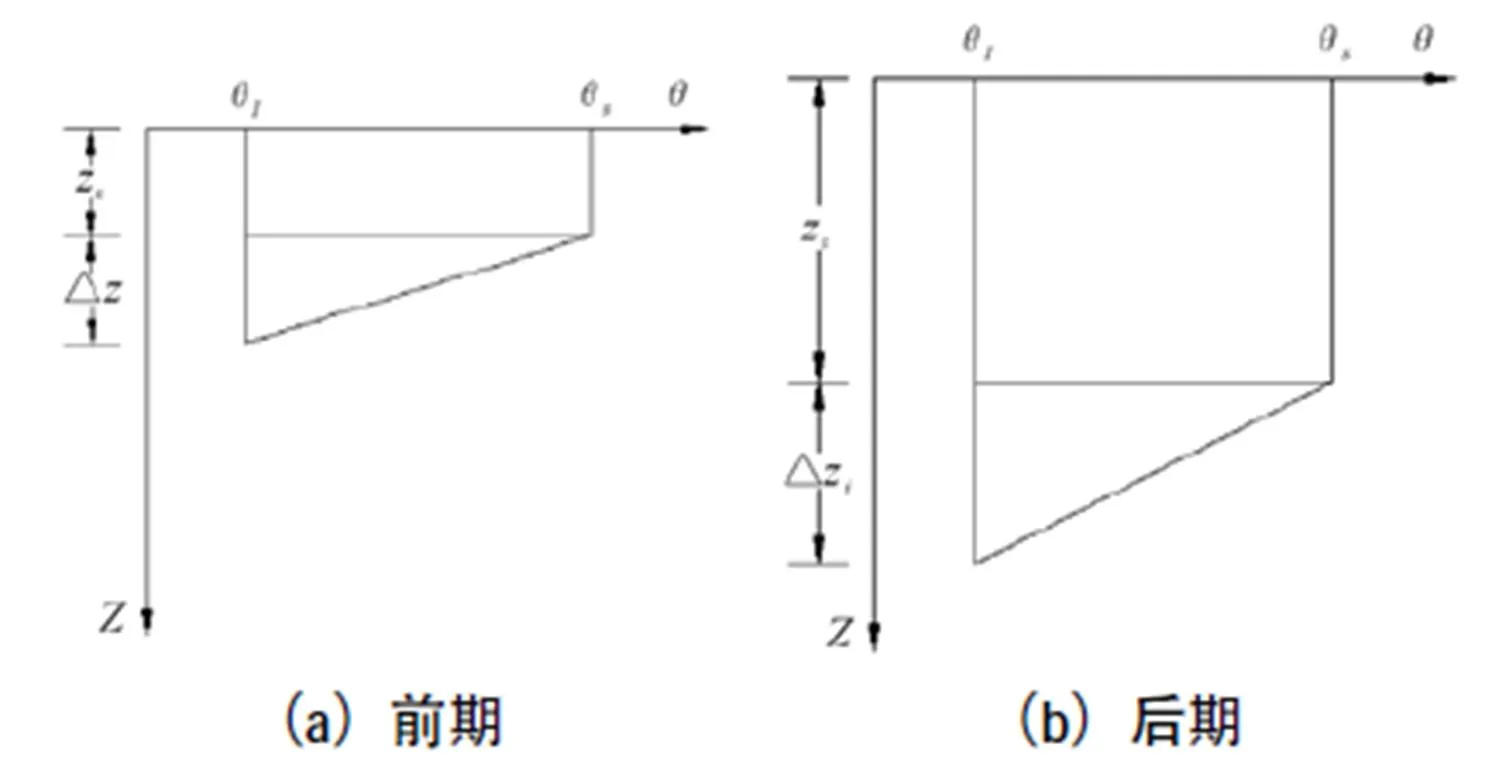
图2 改进Green-Ampt模型假设示意图

1.2.2 模型建立

入渗前期，由达西定律和水量平衡原理，分别可得累计入渗率与累计入渗量：

由累计入渗量与入渗率的关系，并结合式（7）有：

联立式（8）可得：

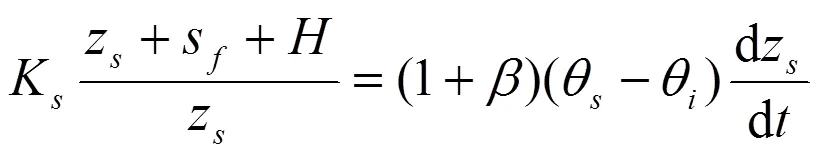
对式（11）积分，并利用0时z=0，则有：

将式（7）、式（9）代入式（12），可得～的关系：

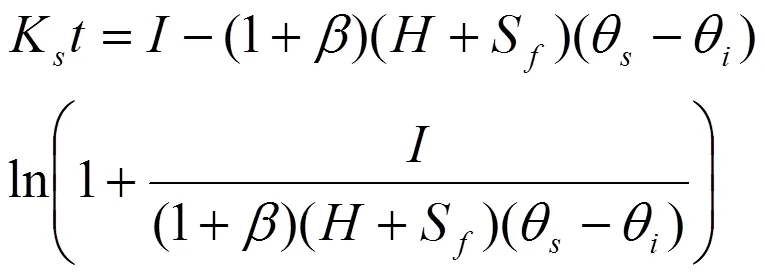
或者：

入渗前期结束时，对应总入渗量为Δ，相应的时间记为t，则有：

进入入渗后期，＞t，累计入渗量与入渗率的关系：

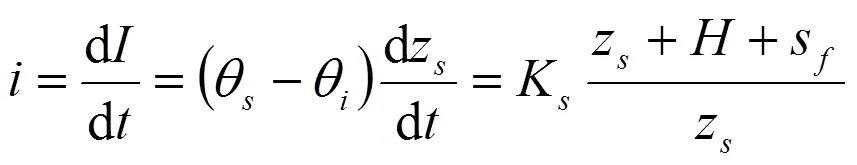
对式（15）积分，并利用z＝Δz时＝t，可得：

式中：Δz为t时刻对应的饱和区厚度，式（9）中，当＝Δ时，s＝Δs，然后联合式（7）、式（9）和式（16），可得：

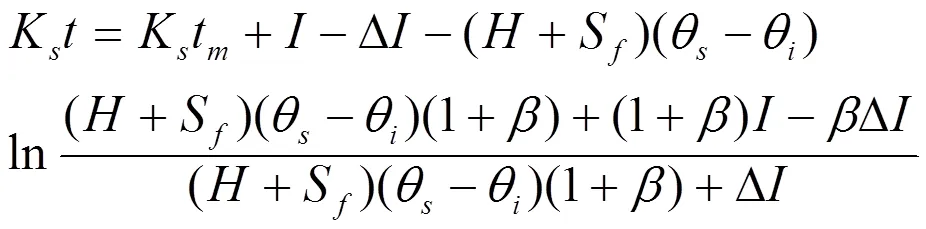
则改进后的入渗时间与总入渗量的关系式为：

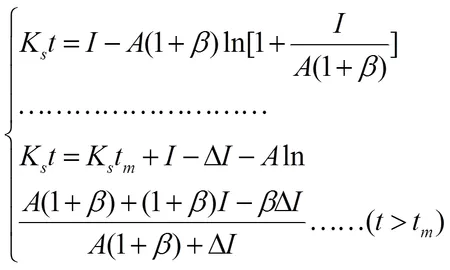
式（18）中参数、、ΔI、K需要通过拟合来确定，确定了4个参数的值后可由式（14）得的值。

2 模型检验

为分析改进效果，使用双环入渗仪，在天津农学院西校区农田水循环试验基地进行入渗试验，实验基地土壤类型为中壤土，在试验过程中人工加水，积水厚度保持在5 cm，共获得6组试验数据，用于测试模型。其中，4组数据（第1组，第2组，第4组，第5组）由小麦（2016年3月20日）地测得，两组数据（第3组，第6组）由玉米（2017年5月18日）地测得。

2.1 模型参数的拟合

分别采用传统模型和改进模型对6组入渗试验数据进行拟合。传统模型使用式（6）进行拟合，拟合目标是使累计入渗时间的观测值和模拟值的误差平方和最小。首先对参数、K设置相应的初始值[15]，然后对参数进行规划求解，使误差平方和最小，计算出传统Green-Ampt模型累计入渗时间的模拟值与观测值的相关系数，以及相应的参数、K值。根据实测资料，由各时段的累计入渗量除以相应的时间，得到各时段的入渗率，选取各组入渗数据最后一个时段的入渗率，近似作为测试的稳定入渗率K，然后，计算测点间参数、K的变差系数，见表1。

改进模型的拟合过程与传统模型类似，不同的是，对常数从小到大设置10个不同的数（1，2，3，4，5，7，10，15，20，25），对于不同的分别进行拟合，并计算相关系数以及各参数的变差系数，结果见表2。

表1 传统模型的参数值

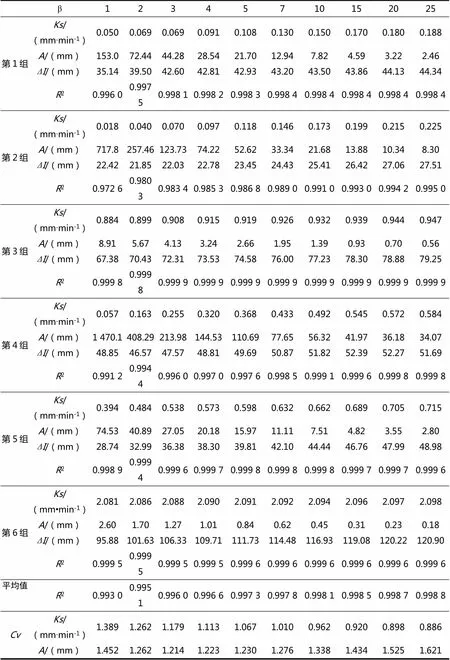
表2 不同β时各组参数值

2.2 拟合结果对比分析

2.2.1值的确定

改进模型的6组相关系数均随的增大而增加，6组相关系数平均值从0.993 0增大到0.998 8，但各组相关系数增大的幅度不同（表2）。其中，第2组相关系数值随增大而增加的幅度最明显，从0.97提高到0.99；第4组数据次之；第1、3、6组相关系数随增大而增加的幅度不明显；第5组数据，当较小时，相关系数有增大的趋势，但当＞15时相关系数出现减小的趋势。综合来看，的取值越大，相关系数越高，但不宜过大。

Δ表示当非饱和区达到最大厚度时，对应渗入的总水量，它与土壤初始含水率和土壤类型有很大关系。整体来看（图3），随着的增大，参数Δ整体呈增大的趋势，但各组参数Δ的拟合值范围不同。当较小时，参数Δ随增大的变化幅度较明显；当≥10时，参数Δ趋于平稳，增加幅度不明显。

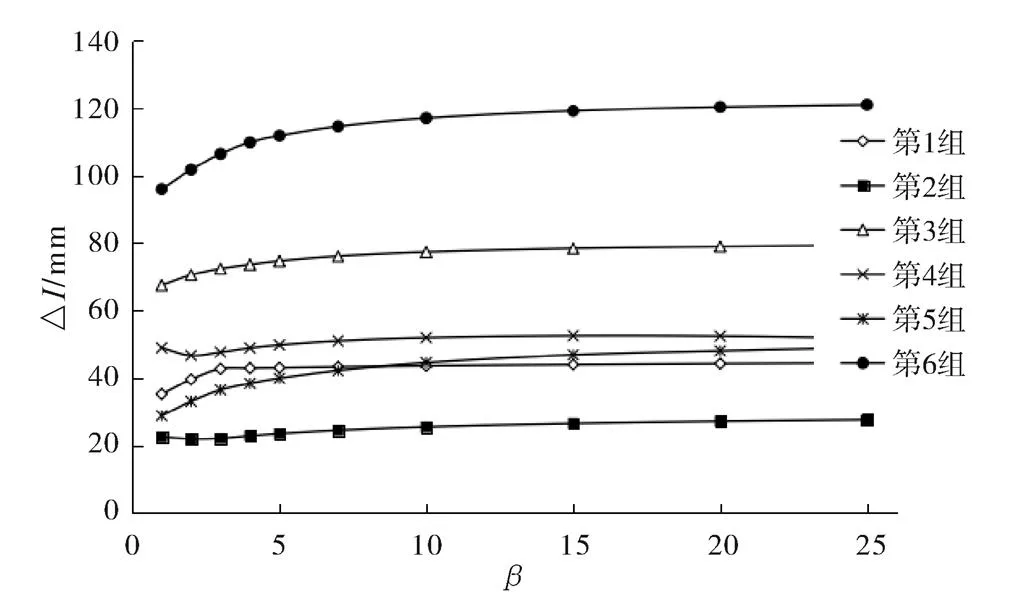
图3 参数ΔI随β的变化趋势

式（18）中的参数K（表2），随着的增大而增大，整体呈增加趋势，增加幅度有所不同，如第2组数据，参数K从0.018增大到0.225，增加幅度较大；第6组数据从2.081增大到2.098，增加幅度较小。当＞15时，各组数据增加幅度均较小，参数K趋于平稳。

参数为模型中的（＋s）（θ-θ），由表（2）可以看出，随着的增大，各组入渗数据对应的参数逐渐减小，同样减小的程度有所不同，其中，第4组参数减小的程度最大，从147 0减小到34；其次是第2组数据，从717减小到8.3；其他4组数据中，值也逐渐减小。当＞15时，参数趋于平稳。

综合来看，取不同值时，不同入渗数据所对应的相关系数均随值的增大而增加，但当＞15时，增加幅度明显减小；各参数（K、A、Δ）随的变化趋势和变化幅度均有所不同，有的随增大而增大，有的随增大而减小，但当＞15时，各参数均趋于稳定，因此，建议取＝15。

2.2.2 拟合效果

整体来看，改进模型较传统模型拟合效果明显提高，传统模型6组相关系数平均值为0.979 0，改进模型计算的相关系数增大到0.998 5。其中，第2、第4组数据效果更为显著，如图5。传统模型和改进模型对入渗后期的拟合效果理想，但入渗前期改进模型的拟合效果要好于传统模型，模拟的累计入渗时间与实测的累计入渗时间的相关系数分别从0.92和0.96提高到0.993 0和0.999 6；其次为第1组数据，其相关系数从0.989提高到0.997；第3、第5、第6组数据，改进模型的相关系数较传统模型也均有所提高。

2.2.3 参数稳定性分析

改进模型的参数（=15）比传统模型的参数更为稳定，并且更接近于实际测试的结果（表1、表2）。其中，改进模型参数K的变化范围（0.170～2.096）明显小于传统模型（0.001～2.068），对应的变差系数分别为0.92和1.59；改进模型参数的变化范围（0.31～41.97）明显小于传统模型（3.4～15 705.3），对应的变差系数分别为1.43和1.61；改进模型参数Δ的变化范围为26.42～119.08，变差系数为0.539，显著小于参数K和的变差系数，不同测试点的参数Δ较参数K和更为稳定。

3 结论

1）基于湿润区分层的假设，对传统Green- Ampt入渗模型进行了改进，得到了一个以分段函数表示的入渗模型。

2）基于实测入渗资料，以累计入渗时间测试值与模拟值误差平方和最小为目标，拟合确定了传统Green-Ampt模型和改进模型的参数值。结果表明，改进模型显著提高了拟合精度，其参数值较传统模型更为合理和稳定，稳定入渗率更接近于测试值。

3）值是改进模型的一个重要参数值，分析表明，改进模型的拟合精度（2）随值的增大而增加，增加幅度快速减小，相应参数随值的增大，其变化幅度均有明显减小的趋势，鉴于此，建议取＝15。

[1] Green W H，Ampt G A．Studies on soil physics: Flow of air and water through soils[J]．Journal of Agriculture Science，1911，4（1）：1-24．

[2] 雷志栋，杨诗秀，谢森传. 土壤水动力学[M]. 北京：清华大学出版社，1998.

[3] 赵伟霞，张振华，蔡焕杰，等．恒定水头井入渗Green-Ampt模型的改进与验证[J]．水利学报，2010，41（4）：464-470．

[4] 郭向红，孙西欢，马娟娟，等．不同入渗水头条件下的Green-Ampt模型[J]．农业工程学报，2010，26（3）：64-68．

[5] 马娟娟，孙西欢，郭向红. 基于Green-Ampt模型的变水头积水入渗模型建立及其参数求解[J]. 水利学报，2010，41（01）：61-67．

[6] 刘姗姗，白美建，许迪，等. Green-Ampt模型参数简化及土壤物理参数的关系[J]．农业工程学报，2012，28（1）：106-110.

[7] Coleman E A，Bodman G B．Moisture and energy conditions during downward entry of water into moist and layered soils[J]．Soil Sci Soc Amer Proc，1945，9（C）：3-11．

[8] Ma Y，Feng S Y，Su D Y，et al．Modeling water infiltration in a large layered soil column with a modifies green-ampt model and HYDRUS-1D[J]. Computers and Electronics in Agriculture，2010，71（s1）：S40-S47．

[9] Bouwer H. Rapid field measurement of air-entry value and hydraulic conductivity of soil as significant parameters in flow system analysis [J]．Water Resources Research, 1966，2（4）：729-738．

[10] Bouwer H. Infiltration of water into non-uniform soil[J].Journal of Irrigation and Drainage Engineering，1969，95 （IR4）：451-462．

[11] 毛丽丽，雷廷武，刘汗，等. 用水平土柱和修正的Green-Ampt模型确定土壤的入渗性能[J]．农业工程学报，2009，25（11）：35-40．

[12] 王文焰，王全九，张建丰，等. 甘肃秦王川地区土壤水分运动参数及相关性[J]．水土保持学报，2002，16（3）：110-113．

[13] 彭振阳，黄介生，伍靖伟，等. 基于分层假设的Green-Ampt模型改进[J]. 水科学进展，2012，23（1）：59-66.

[14] 周鑫洋，王仰仁，刘群昌. 四个入渗公式对农田潮土的适应性研究[J]. 灌溉排水学报，2015，34（8）：96-100.

[15] 沈洪政，王仰仁，韩娜娜. 非线性入渗模型求参中参数初始值确定方法研究[J]. 中国农村水利水电，2017 （10）：183-187.

责任编辑：宗淑萍

Improvement of Green-Ampt model based on layered assumptions in wetting regions

LI Yong-lin1,2, WANG Yang-ren1,2,Corresponding Author, SUN Xiao-ping3, ZHENG Zhi-wei1,2

（1. College of Water Conservancy Engineering, Tianjin Agricultural University, Tianjin 300384, China; 2. University-Enterprise Collaborative Innovation Laboratory of Water-Saving Irrigation Technology and Equipment, Tianjin 300384, China; 3. Shanxi Institute of Water Resources and Hydropower Research, Taiyuan 030012, China）

It is assumed that the infiltration process is divided into two stages of pre-infiltration and post-infiltration. The ratio of soil saturated zone to unsaturated zone is a constant 2in the pre-infiltration stage, and the thickness of unsaturated zone increases with infiltration. The thickness of unsaturated zone in the post-infiltration stage no longer changes with time, which is a fixed value，and only the thickness of saturated zone changes with time. Based on this, Green-Ampt model is improved. The traditional Green-Ampt model and improved model were used to fit six groups of infiltration test data. The correlation coefficient of traditional model fitting was 0.982（the average of six groups of data）. Compared with the traditional model, the fitting accuracy of the improved model was obvious. The correlation coefficient was increased by 0.016, reaching 0.998 （corresponding to=15）. The data of two groups were especially effective, which were increased by 0.07 and 0.04 respectively, both reaching over 0.99. The improved model has the same strong physical meaning as the traditional model. However, compared with the traditional model, the stable infiltration rate obtained by the improved model is closer to the test value and the improved model has wider applicability.

Green-Ampt infiltration model; accumulated infiltration capacity; unsaturated zone; infiltration front; infiltration time

1008-5394（2018）03-0078-06

10.19640/j.cnki.jtau.2018.03.017

S275

A

2018-05-01

国家自然科学基金项目（51779174）；天津市农业科技成果转化与推广项目（201701150）；天津市科技计划项目（17YFZC SF00930）；山西省水利科学技术研究与推广项目（201618）

李泳霖（1994-），男，硕士在读，主要从事灌溉排水理论与新技术研究。E-mail：335985474@qq.com。

王仰仁（1962-），男，教授，博士，主要从事灌溉排水技术研究。E-mail：wyrf@163.com。