留数定理在实积分中的应用研究

徐建中

（亳州学院，安徽 亳州 236800）

积分的计算在高等数学中有着举足轻重的地位，尤其是在许多交叉学科领域有着广泛的应用。但是在实际的计算过程中，有许多形式的被积函数，原函数不易求出，导致结果无法积出来。而复变函数中的留数定理正好为此类问题提供了重要的理论计算方法。

对于那些难于用解析方法求解的实变函数，我们可以用留数定理加以解决，主要解决思路是将实变函数转化复变函数，借助留数定理进行积分计算、求解。主要是先将其转化为沿闭合回路曲线的积分，然后将问题转化为求解闭合回路内部各个孤立奇点处的留数值，最后，利用留数定理得到被积函数的解，本文主要运用留数定理举例说明并加以归纳总结，以其强调留数定理在积分计算中的应用。

定理1（留数定理）:设函数f(z)在回路所围l区域B上除有限孤立奇点b1,b2,…,bn外解析，在闭区域B上除b1,b2,…,bn外连续，则:

显然，留数定理计算的主要思路就是将回路积分转化为被积函数在回路所围区域上各奇点的留数之和。

1 留数定理在实变函数积分中的应用

1.1 计算类型积分

解：按照公式（2）知：

例2：计算积分

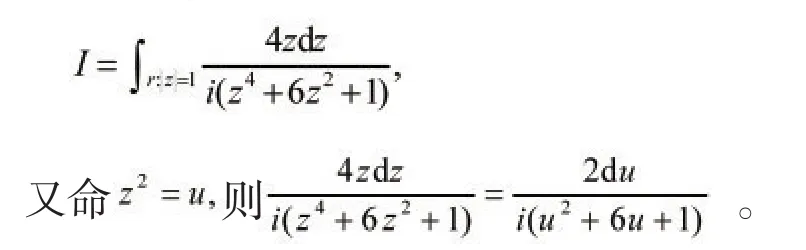
当z绕Γ圆周一周时，u亦在其上绕二周，故

被积函数f(u)在Γ内部仅有一个一阶级点

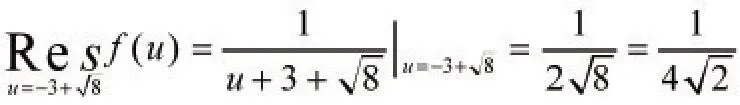
所以由留数定理，

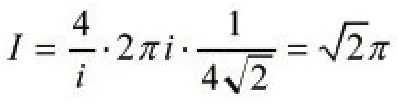
若R（cosθ，sinθ）为θ的偶函数，则之值亦可由上述方法求之。因此时

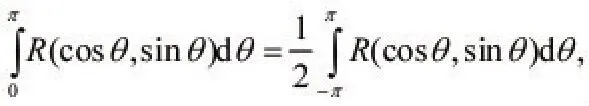
1.2 计算类型积分

为了计算这种反常积分，我们先证明一个引理。它主要用来估计辅助曲线上的积分。

引理1设F（z）沿圆弧充分大）上连续，且

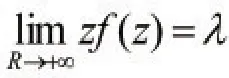
于SR上一致成立（即与θ1≤θ≤θ2中的θ无关），则

例3：设a＞0，计算积分

它一共有四个一阶级点

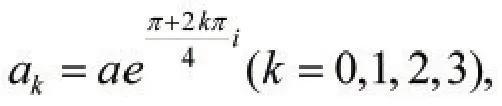
且符合定理

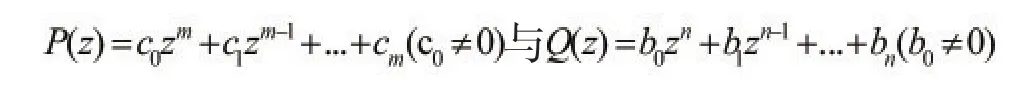
为互质多项式，且符合条件：（1）n-m≥2；（2）在实轴上Q（z）≠0，于是有：

1.3 计算类型积分

引理2（若尔当引理）设函数g(z)沿半圆周ΓR∶z＝Reiθ（0≤θ≤π，R充分大）上连续，且在ΓR上一致成立。则：

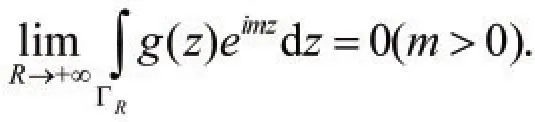
证理：对于任给的ε＞0，存在R0(ε)＞0，使当R＞R0时，有

于是，就有

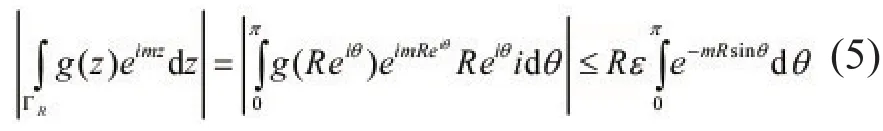
于是，由（若尔当不等式）

将（5）化为

定理2：设，其中P（z）及Q（z）是互质多项式，且符合条件：

（1）Q（z）的次数比P（z）的次数高，

（2）在实轴上Q（z）≠0

（3）m＞0，

则有:

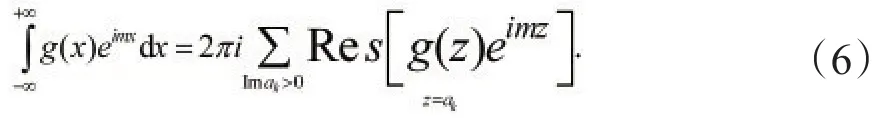
例4：计算积分

解：被积函数为偶函数，故

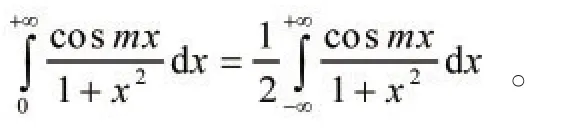
根据定理1，则有：

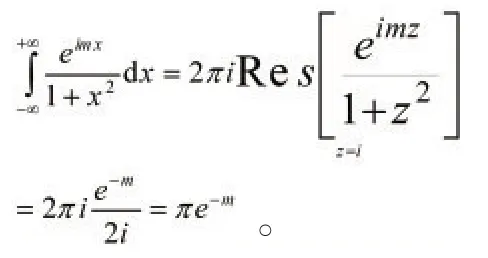
则有：

总之，留数理论是复变函数论中一个非常重要的理论，只要我们在解决问题中灵活运用该理论可以达到事半功倍的效果，也有助于为定积分的计算提供新的思路，更好的解决实际问题中积分计算。