一种基于图像插值运算的Laplace算子边缘检测方法*

2018-10-19杨鹏

浙江工贸职业技术学院学报 2018年3期

杨鹏

（浙江工贸职业技术学院，浙江温州325003）

0 引言

数字图像包含着丰富的视觉信息，尤其是图像中的边缘信息，如图像中河流的边缘信息、医学CT图像中人体骨骼的边缘信息、道路交通图像中各种斑马线的边缘信息等。边缘信息的提取被广泛的应用于现代生活中，如医疗辅助诊断、人脸识别、目标跟踪、遥感监测等不同领域，这些边缘信息对于图像中目标的识别与检测有着十分重要的意义。

边缘是一类特殊像素点的集合，这些特殊像素点是由图像中不同属性目标之间的边界组成的，在图像的灰度值上表现为灰度值的不连续性。由于图像中避免不了会存在少量噪声，而图像噪声与边缘信息都代表着图像中的一种高频信息，即在边缘检测的同时也对噪声进行了放大，以及复杂的图像纹理信息，导致了精确的图像边缘检测变得十分具有挑战性。目前，已有许多研究者提出了很多不同类型的边缘检测方法，如Roberts边缘检测算子、Sobel边缘检测算子、Prewitt边缘检测算子、Kirsch边缘检测算子以及Canny边缘检测算子[1-4]等。Canny边缘检测算子是一种基于优化理论的边缘检测算子，在边缘检测精度以及抗噪声等方面有较好的表现，但是该算子需要对所涉及到的高斯滤波参数和高低阈值手动的进行选择，在适应性方面还存在一定的缺陷[5]。Laplace边缘检测算子是一种二阶导数算子，具有旋转不变性和位移不变性的优点，但是也存在一定的缺陷，如在边缘检测过程中可能会丢失边缘方向信息及可能会加重噪声对边缘检测结果的不利影响等。

本文基于原有的Laplace边缘检测算子，提出了一种基于图像插值运算的Laplace算子边缘检测方法，旨在一定程度上克服原有Laplace算子的不足，提高图像边缘检测的精度和边缘检测的抗噪性。

1 Laplace算子

Laplace算子是一种二阶导数算子，是基于图像两个坐标轴方向上的二阶偏导数定义而来的一类边缘检测算子。数字图像g(x,y)在x轴和y轴方向上的二阶偏导数定义如式(1)所示：

图像的边缘部分往往是灰度变化、跳跃较大的部分，因此边缘部分对应的一阶偏导数往往是局部的极值，结合式(1)可以看出图像的边缘区域对应着二阶偏导数过零点时对应的位置，因此可以通过图像二阶偏导数的过零点来对图像的边缘进行检测。在Laplace算子的应用领域，常用的Laplace算子可以定义成如下几种形式：

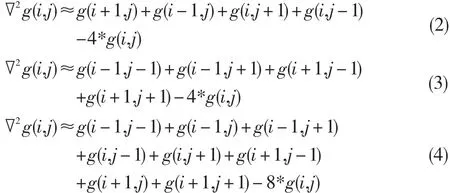
式（1）、（2）和（3）所示Laplace算子对应的模板分别如图1（a）、1（b）和1（c）所示。从图1可以看出，1（a）所对应的Laplace模板对垂直和水平方向的边缘检测效果较好，1（b）所对应的Laplace模板对两个对角线方向的边缘检测效果较好，而1（c）所对应的Laplace模板则对这几个方向的边缘检测均有效。从该图可以发现，原有Laplace算子在边缘检测时是各向同性的，利用该算子虽然可以对图像的边缘进行锐化处理，但是该算子对噪声及其敏感，通过二阶偏导数的过零点对边缘进行检测极易受噪声的影响，有可能获得不可靠的图像边缘信息。

本文针对原有Laplace模板存在的问题，提出了一种基于图像插值运算的Laplace算子进行边缘检测，该改进后的Laplace算子在原图图像的插值运算基础上进行展开，一方面可以克服Laplace算子各向同性的问题，同时也能减少噪声对边缘检测的影响。

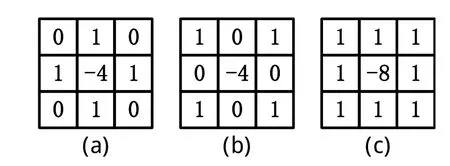
图1 常用Laplace模板

2 改进的Laplace算子

为减少噪声对边缘检测效果的影响，同时提高边缘检测的效果，本文采用插值的方法对原图像进行扩展，具体的扩展方法是对原图像中行与行之间的像素通过插值运算得到新的一行像素，同样的对原图像中列与列之间的像素通过插值运算也可以得到新的一列像素。图2以一幅大小为3×3的图像为例进行说明，2（a）是插值之前的原图像，2（b）是通过插值后获得的新图像。

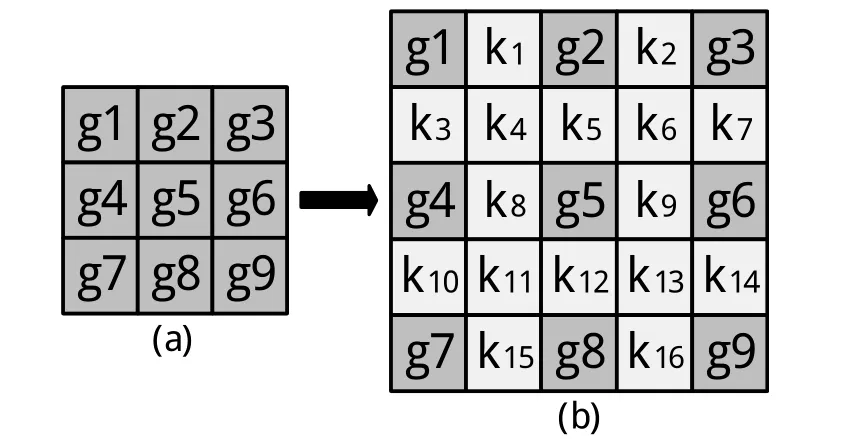
图2 图像插值前后示意图

对大小为3×3的图像进行插值可以获得一个大小为 5×5 的图像，图 2（a）中的 g1、g2、g3、g4、g5、g6、g7、g8和g9分别表示原图像的像素值，而图 2（b）中的 k1、k2、k3、k4、k5、k6、k7、k8、k9、k10、k11、k12、k13、k14、k15、k16是通过对原图像进行扩展插值而获得的新的像素值。具体新的像素值的获取方式如式（5）所示，主要以k1、k2及k3为例进行说明，其它的类似。

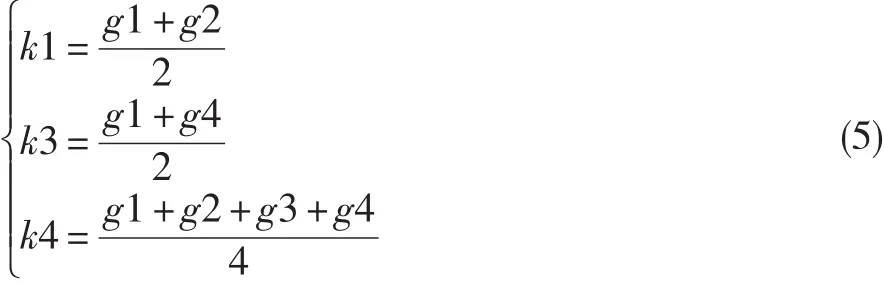
通过该种图像插值方式对原图像进行了扩展，为适应扩展后的新图像，对原Laplace算子进行相应的改进，以适应新的图像，具体改进后的Laplace模板如图3所示，该模板所对应的Laplace算子如式（6）所示。

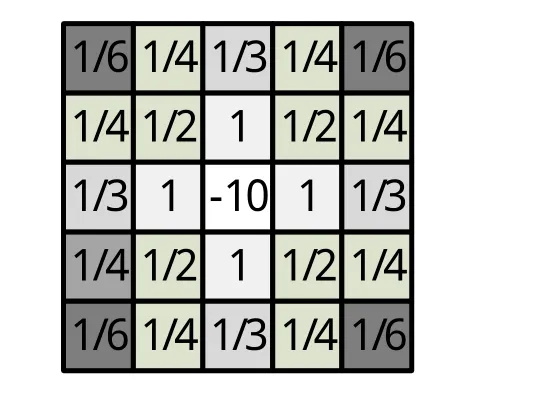
图3 改进后的Laplace模板

其中g(x,y)表示对应的图像，x、y表示相应的横坐标和纵坐标。

具体的图像插值代码如下所示（matlab代码）：运行该代码对House图像进行插值运算，House图像及插值运算后获得的图像如图4所示。

图4 House原图及插值后获得的图像

改进之前的Laplace模板只考虑了水平方向、垂直方法或对角方向，从图4可以看出改进后的模板可以检测更多的边缘信息，同时给不同方向的边缘分配了不同的权重，离模板中心点越近的方向其权重越大。通过对插值以后的图像运用该模板进行边缘检测，可望提高边缘检测的精度。

3 实验结果与分析

为验证本文所提出的基于图像插值运算的Laplace算子边缘检测方法的效果，以House图像为实验对象进行展开，如图5（a）所示。主要通过对比本文所提出的边缘检测方法与原有Laplace边缘检测方法及一些改进的Laplace边缘检测方法的边缘检测效果来进行说明。原有的Laplace边缘检测方法主要由三类不同的Laplace边缘检测模板组成，这三类模板分别是水平垂直方向的Laplace边缘检测模板（与图1（a）对应）、对角线方向的Laplace边缘检测模板（与图1（b）对应）、水平垂直及对角线8个方向的Laplace边缘检测模板（与图1（c）对应）；改进型的Laplace边缘检测方法主要包括文献[6]、文献[7]及文献[8]中改进的Laplace边缘检测方法。

图5展示了不同Laplace算子边缘检测时的检测效果，从该图可以很直观的看出本文改进了的Laplace边缘检测方法相对于原Laplace边缘检测模板及已有改进的Laplace边缘检测方法，其边缘检测效果是最好的，检测精度存在很大的提升。这充分证实了本文所提出的基于图像插值运算的Laplace算子边缘方法的有效性。