高考数学创新型试题的几种类型

■河南省信阳高级中学 陈荣军

高校要选拔具有创新潜质的人才,高考数学必须重视对学生创新意识的考查。考生的创新意识表现为:对新颖的信息、情境的设问,能选择有效的方法和手段分析、处理信息,综合与灵活地应用所学的数学知识、思想和方法,进行独立的思考、探索和研究,提出解决问题的思路,并创造性地解决问题。近几年来,在全国及各省市的各套高考数学试卷中出现了一些创新型试题,这些试题主要类型有直觉思维型、学习迁移型、实际应用型等。本文拟对高考数学创新型试题的类型作一些分析。

一、直觉思维型

直觉思维是指个体以已有的知识经验为基础,无须逻辑推理,对突然出现的新问题和新现象,能迅速理解并作出判断的思维方式。直觉思维可以帮助同学们洞察数学本质、猜想数学结论、发现数学规律等。直觉思维是快速解答一些高考数学试题的利器。鉴于直觉思维的重要作用,在高考数学试题的命制中,很自然地要考查同学们的直觉思维。直觉思维型的试题主要有整体观察型、直觉判断型、类比联想型、归纳猜想型、极限洞察型等。

例1 四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯,如图1所示。

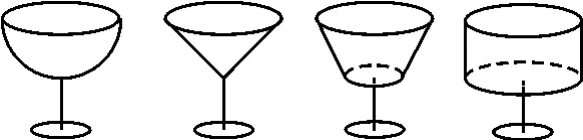
图1

盛满酒后他们约定:先各自饮杯中酒的一半。设剩余酒的高度从左到右依次为h1,h2,h3,h4,则它们的大小关系是( )。

A.h2＞h1＞h4B.h1＞h2＞h3

C.h3＞h2＞h4D.h2＞h4＞h1

点评:本题背景鲜活,颇有生活气息。命题者大胆地将四种旋转体汇集在一起,与日常生活中的酒杯形状联系起来,巧妙设问,主要考查几何体的体积与高度的关系,考查同学们的空间想象能力及直觉思维能力。通过整体观察,不需具体计算,进行直觉思维,对问题作出迅速、准确的直觉判断。因为各酒杯杯口半径相等,即上底面积相等。内空高度相等,且饮去上部一半,故下部越细,剩余酒高度越高,所以有h2＞h1＞h4。故选A。

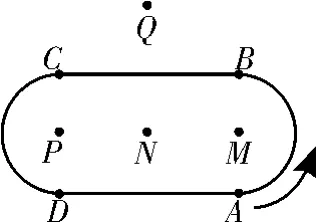
图2

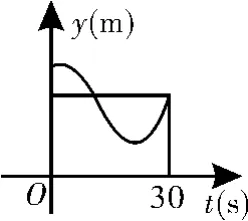
图3

跟踪练习1 小明在如图2所示的跑道上匀速跑步,他从点A出发,沿箭头方向经过点B跑到点C,共用时3 0s,他的教练选择了一个固定的位置观察小明跑步的过程,设小明跑步的时间为t(s),他与教练间的距离为y(m),表示y与t的函数关系的图像大致如图3所示,则这个固定位置可能是图2中的( )。

A.点 M B.点 N

C.点P D.点Q

解析：分别假设这个位置在点M、N、P、Q,然后结合函数图像进行判断,利用排除法即可得出答案。选项A,假设在M处,则A至B段y为常数,与函数图像不符,故A错误。选项B,假设在N处,则A与C处y的值相同,与函数图像不符,故B错误。选项C,假设在P处,则3 0s时y的值最小,与函数图像不符,故C错误。经判断点Q符合函数图像。故选D。

二、学习迁移型

解答学习迁移型试题 ,需要同学们具有自主学习和迁移的能力。学习能力是同学们阅读并理解数学新知识的能力,这里的新知识可以是新的概念、新的定理、新的方法、新的公式、新的规则等。学习能力包括会搜集、提炼、加工信息,对阅读的内容进行概括和理解,看清问题的本质,然后运用新的知识通过分析、演算、归纳、猜想、类比或论证等方法解决一些新的数学问题。

例2 设P是一个数集,且至少含有两个数,若对任意a、b∈R,都有a+b、a-b、数b≠0),则称P是一个数域。例如有理数集Q是数域;数集F={a+b2|a,b∈Q}也是数域。有下列命题:

点评:本题设计独特、情境新颖,具有很强的抽象性和发散性。从试题的背景来看,此题以近世代数中“群、环、域”的知识为背景,试题展示给同学们的是一个全新的问题,体现了自主学习和主动探究精神。从试题的立意来看,本题是一道能有效考查同学们的阅读理解能力、抽象与具体转化能力、构造法和反例思想方法的创新型试题。从试题的解答来看,直接以“数域”的定义为背景的试题在各种复习资料和模拟试题中从未见过,解决这个问题没有现成的套路和招式,需要同学们阅读理解“数域”的定义,综合运用多种数学思想方法,分别检查所给答案是否同时满足“数域”定义的四个条件(满足需证明,不满足需举反例),才能解决问题。这类以高等数学知识为背景的问题,能有效考查同学们进一步学习的潜质,已成为高考试题的一大亮点和热点,值得注意。

跟踪练习2 对定义在区间D上的函数f(x),若存在常数k＞0,使对任意的x∈D,都有f(x+k)＞f(x)成立,则称f(x)为区间D上的“k阶增函数”。已知f(x)是定义在R上的奇函数,且当x≥0,f(x)=|xa2|-a2。若f(x)为R上的“4阶增函数”,则实数a的取值范围是____。

解析：当x≥0,f(x)=|x-a2|-a2时,令f(x)=0,则y=f(x)有最大的零点是2a2,由y=f(x)是奇函数,所以y=f(x)有最小的零点是-2a2。把横坐标向左平移4个单位得到y=f(x+4)的图像,且y=f(x+4)有最大的零点为2a2-4。因为y=f(x)为R上的 “4阶增函数”,则对任意的x∈R,都有f(x+4)＞f(x)恒成立,即函数y=f(x+4)的图像在函数y=f(x)的图像上方,由图4可知,2a2-4＜-2a2,即a2＜1,故a的取值范围是(-1,1)。

图4

三、实际应用型

“坚持数学应用,考查应用意识”是多年以来一贯坚持的命题方针。应用题是对同学们“综合实力”的考查,是考查能力与素质的良好题型,近几年应用题的编拟更加重视语言简洁、准确,背景清新、近人,模型具体、简明,方法熟悉、简便,所涉及的都是数学基本内容、思想和方法,摒弃烦琐的数学运算,突出对数学思想、方法和实践能力的考查,彰显数学在解决实际问题中的重要作用。

例3 图5是某汽车维修公司的维修点环形分布图。公司在年初分配给A、B、C、D四个维修点某种配件各5 0件。在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为4 0、4 5、5 4、6 1件,但调整只能在相邻维修点之间进行。那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为( )。

A.1 5 B.1 6 C.1 7 D.1 8

解析：D处的零件要从A、C或B处移来调整,且次数最少。方案一:从A处调1 0个零件到D处,从B处调5个零件到C处,从C处调1个零件到D处,共调动1 6件次。方案二:从B处调1个零件到A处,从A处调1 1个零件到D处,从B处调4个零件到C处,共调动1 6件次。故选B。

图5

点评:本题是一个优化安排的问题,需要同学们综合运用已有的知识经验,通过各种调整的操作试验与尝试才能解决问题。此题提高了对分析问题和解决问题的能力要求,大大增加了思维量,很好地考查了同学们的实践能力和数学应用意识。

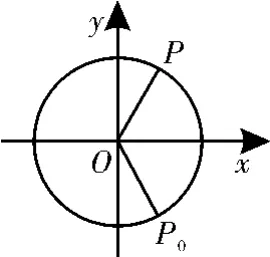
图6

跟踪练习3 如图6,质点P在半径为2的圆周上逆时针运动,其初始位置为P0,-),角速度为1,那么点P到x轴的距离d关于时间t的函数图像大致为图7中的( )。

图7

解法一：(排除法)当t=0时,P点到x轴的距离为2,排除A、D,由角速度为1知,落在x轴上,即P点到x轴的距离为0。故选C。