基于有限元分析的CT修正胸腔建模与感生磁场计算的研究*
2018-10-18陈瑞娟冯彦博赵喆王金海王慧泉李光旭
陈瑞娟,冯彦博,赵喆,2,王金海,王慧泉,2△,李光旭,2
(1. 天津工业大学电子与信息工程学院,天津 300387; 2.天津工业大学天津市光电检测技术与系统重点实验室,天津 300387; 3.天津市医学电子诊疗技术工程中心,天津300387)
1 引 言
根据国家癌症中心发布的《2017中国城市癌症最新数据报告》,肺癌仍然是我国发病率、死亡率第一的癌症。目前,肺部肿瘤检测技术主要有X射线断层成像、磁共振成像、正电子发射断层成像,三种检测设备体积较大,对使用环境有特殊要求。除此之外,X射线断层成像与正电子发射断层成像对人体具有一定的辐射危害,不能做日常重复检查和实时连续监测[1]。磁探测电阻抗成像技术作为一种新型无创成像技术,是对传统医学影像技术的重要补充,在肺部动态成像中有重要的应用前景。
磁探测电阻抗成像利用成像体周围的磁场分布信息来重建成像体断层电导率分布图像[2],是电阻抗成像技术(electrical impedance tomography, EIT)的一个重要分支,具有费用低,便于携带,无损检测等多种优势[3]。1992年,Ahlfors等[4]首次提出磁阻抗成像(magnetic impedance tomography,MIT)的概念,并通过实验证明通过测量外部磁场值可以对成像体内部电导率变化进行定位。1999年,Tozer[5]等提出MIT数据采集系统原型,并通过实验证明由磁场重建二维电流密度分布的可行性。2004年,Ireland等[6]将此技术更名为磁探测电阻抗成像,并证明其数据采集和活体电流密度成像的技术可行性。在国内,天津大学李刚课题组将MDEIT应用于三维人体经络定位[7],并围绕MDEIT的若干关键问题进行深入研究,优化数据采集方式[8],提出环形激励电极[9]和全变差正则化重建算法[10]等,有效地推进MDEIT的发展。
目前,EIT已经广泛应用于肺部监护中[11],其首批临床应用成果于2010年取得国际质量体系认证[12]。作为三维应用技术,MDEIT主要解决了EIT中表面放置检测电极问题[6],其应用磁场采集线圈在成像体周围的空间中采集磁场分布数据,数据位置和数量不受成像体表面的约束,不存在接触阻抗的影响,避免了数据失真和系统阻抗匹配的问题。本研究将MDEIT应用于肺部肿瘤检测,从胸腔CT图像中获取关于胸腔解剖结构的先验信息进而构建胸腔三维模型,通过仿真计算获得肺部肿瘤患者与正常人胸部周围磁场分布的差异性特征,从而为MDEIT应用于肺部肿瘤检测提供理论依据。
2 磁探测电阻抗成像及正问题理论基础
图1为磁探测电阻抗成像系统示意图。激励电流I通过电极注入成像体从而在成像体周围激发磁场,利用磁场采集线圈采集成像体周围的磁场分布数据,从而重建成像体内部电导率分布。

图1 磁探测电阻抗成像系统
贴在目标区域Ω边界∂Ω上的电极向成像体注入电流I,在目标体内部会产生与电导率σ相关的电势分布和电流密度分布。根据Maxwell方程和Ohm定律可知,Laplace方程适用于目标区域Ω内部的电势φ和电导率σ分布,见式(1)。
·σφ=0
(1)
在边界∂Ω上满足Neumann边界条件,则有式(2)。

(2)
其中,φ(s)为区域Ω内一点的电势;n为边界∂Ω上法线单位向量;j为给定边界上注入电流的电流密度向量。将式(2)经过变换得到式(3)。
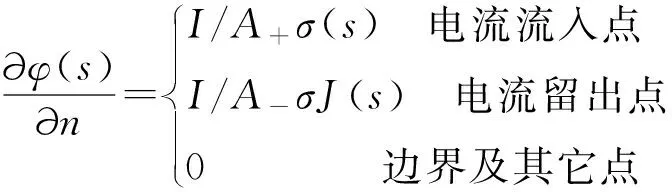
(3)
其中,A+为电流注入电极的面积,A-为电流流出电极的面积。
根据电导率分布σ和Neumann边界条件,求解 Laplace方程可以得到电势φ的分布,进而目标区域Ω内部的电流密度见式(4)。
J=-σφ
(4)
在此基础上,通过Biot-Savart定律可以求出目标体外部的磁感应强度,见式(5)。

(5)
其中,μ0为真空磁导率;r′=(x′,y′,z′)为场点;r=(x,y,z)为源点。
3 胸腔解剖结构提取与建模
胸腔内不同器官、组织层叠交错分布,构成具有复杂电导率分布的导体。图2(a)为肺癌患者胸腔CT图像,该图像源于肺部图像数据库联盟(the lung image database consortium,LIDC)[13]。CT图像是以不同的灰度值来表示不同的器官和组织对于X射线的吸收程度的一种医学成像方法,黑影区域表示低密度区,白影区域表示高密度区。根据不同组织对X射线的吸收程度以及其在胸腔位置分布的经验值,在图2(a)胸腔CT图像中可以清晰的辨别出,1为肌肉组织,2为肺,3为心脏,4为骨组织,5为肺部肿瘤组织。

图2 肺肿瘤患者胸腔CT图像
为获取胸腔内器官形态结构以及空间位置分布,对肺癌患者的CT图像进行图像分割以提取胸腔内的空间构成,图像分割采用灰度阈值分割算法,首先对CT图像进行区域均值滤波以滤除噪声与误差,同时优化像素分布,依据组织器官特征与灰度值的对应关系进行区域分割,所得分割图像的像素分布与原始图像保持一致,图2(b)为图像分割结果。
依据CT图像的分割结果,实验构建正常人和肺部肿瘤患者的胸腔三维模型,见图3、图4。为保证胸腔空间结构的一致性,将肺癌患者肿瘤组织区域移除,从而构建正常人胸腔三维模型。模型成像区域半径为0.25 m,高度为0.5 m。依据已有的生理数据[14],在10~100 kHz测量频率之间,肺容积为5 000 mL,电导率为0.04 S/m,内部的肿瘤体积为150 mL,电导率为1.45 S/m。模型其余部分设定为肌肉,电导率为0.5848 S/m[15]。

图3 正常人胸腔模型
针对本次研究,图像分割保留了胸腔、肺组织、肿瘤组织的生理形态,以及相互之间的空间相对位置。利用从CT图像中提取到的关于胸腔解剖结构的先验信息对胸腔进行建模,提高了胸腔模型与真实胸腔的相似度,为磁探测电阻抗成像正问题计算提供可靠支撑。

图4 肿瘤患者胸腔模型
4 数值计算与分析
正问题的求解采用有限元分析方法,在给定边界条件下,首先对模型的电势分布进行求解,其次对模型电流密度求解,进而计算模型外采集点处的磁感应强度,在此给出仿真计算的具体算法。
见图5(a),将模型剖分为64×64×10个单元,剖分单元的大小与CT扫描的体素一致。在目标体表面贴放一对长方形电极,忽略电极厚度,电极大小为1 cm×10 cm,电流频率为31.25 kHz,电流强度为5 mA,方向沿X轴由左至右。见图5(b),测量平面平行于X-Y平面且位于肺部中央,在此平面上从圆心位于肺部中心且半径为0.5 m的圆上等角度间隔地拾取36个测量点,将此36个测量点作为场点收集成像体周围磁感应强度数据。

图5 模型剖分与采样点示意图
在第二类边界条件下,采用变分方法对场域方程进行离散化处理,得式6所描述的离散结果[16]。

(6)
其中φj为剖分节点的电势;σ为单元的电导率;Nj为基函数;Jn为电流;i,j=1,2,...n,n为剖分节点总数。将式(6)改写成矩阵形式,见式(7)。
(7)

Nj为基函数,本次研究中的剖分单元为立方体,则立方体的基函数可以由式(8)中的插值函数获取,假设a、b、c、d、e、f、g、h为待定常数,
(8)
由于激励电极选为片电极,落在边界单元的面上,假设注入电流的量值为I,单元的面积为Δ,则
(9)
由此可以计算模型剖分单元节点上的电势值,进而依据式(4)计算出模型内的电流密度分布。在此基础上,应用Biot-Savart定律计算模型外部的磁感应强度。式(10)为Biot-Savart定律离散化公式。
(10)
其中Bj为第j个采样点的磁感应强度矢量,Ji是第i个单元的电流密度矢量,Vi是第i个单元的体积。rj是第i个单元单元的中心到测量点的矢量。i=1, 2 ....n,n为剖分单元总数。利用以上公式,计算得到图6、图7、图8、图9的电势、电流密度、磁感应强度的分布,本次仿真实验是在Matlab软件平台上完成的。
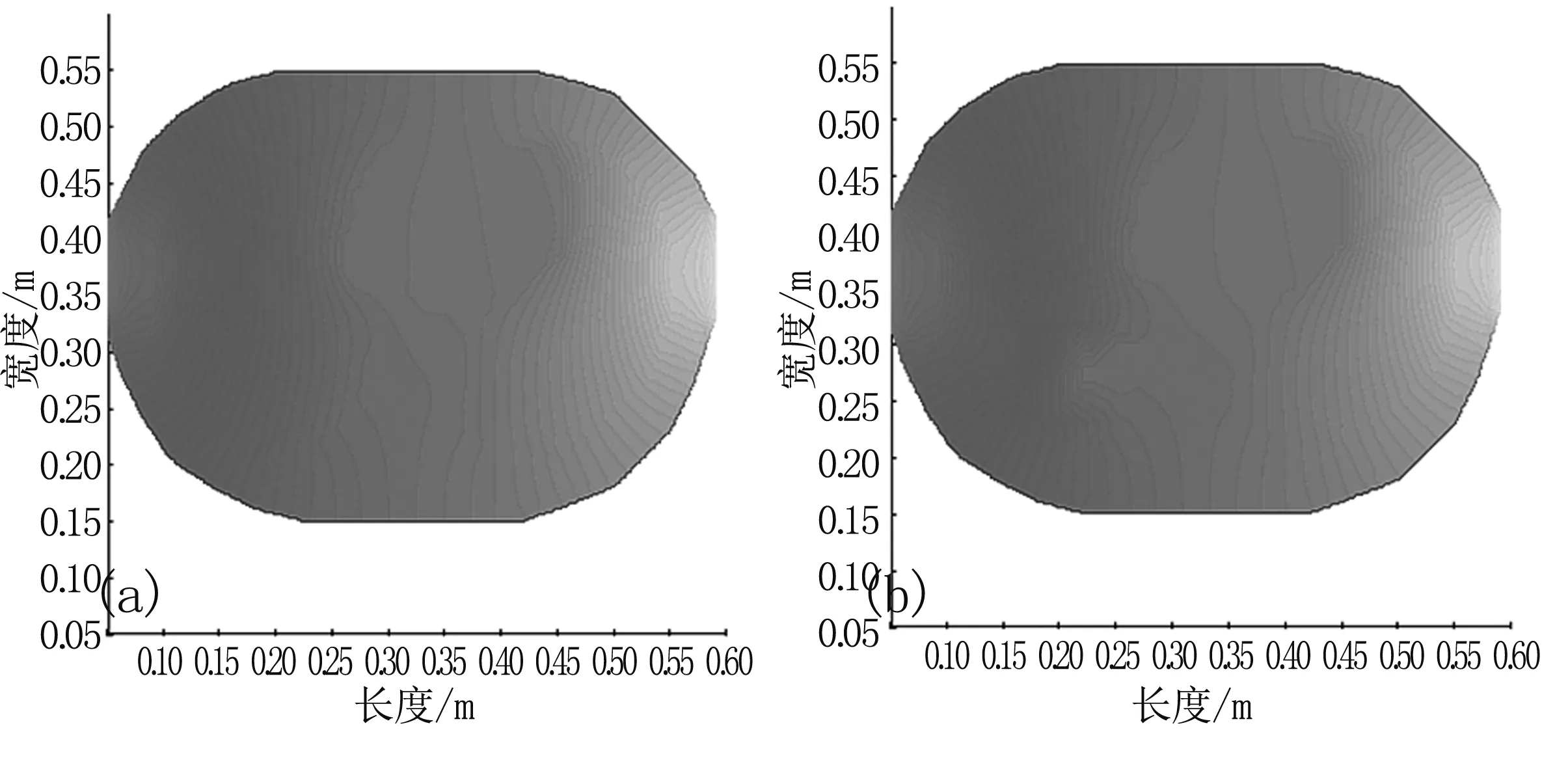
图6 正常人(a)与患者(b)模型电势分布
Fig6Potentialdistributionofnormalhuman(a)andpatient(b)
由图6和图7中可以看到,在给定的模型和激励信号下,电势、电流密度随胸腔内部阻抗分布的差异产生相应的特异性分布,直观来看可以辨识胸腔内部基本结构。

图7 正常人(a)与患者(b)模型电流密度分布
Fig7Currentdensitydistributionofnormalhuman(a)andpatient(b)
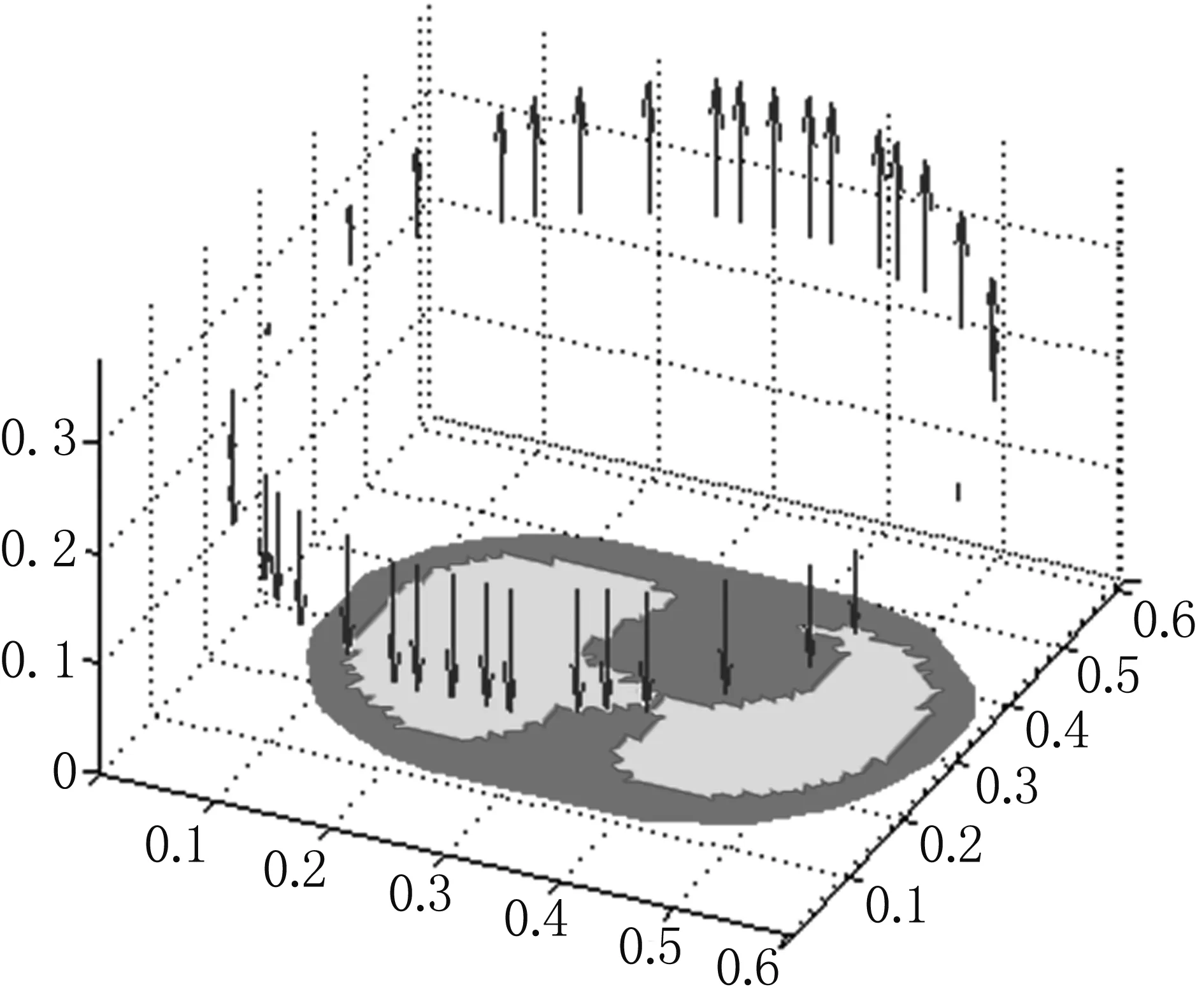
图8 正常人模型磁感应强度矢量图
Fig8Vectorgraphofmagneticinductionintensityofnormalhumanmodel

图9 患者模型磁感应强度矢量图
Fig9Vectorgraphofmagneticinductionintensityofpatientmodel
由图8和图9可以看到,胸腔外部周围的感应磁场垂直于电流方向,从本次采集点的计算值来看,在模型中间位置磁感应强度值较大,靠近电极部位的磁感应强度值逐渐减小。图10中,对正常人和肺部肿瘤患者的磁感应数据的具体数值进行对比分析,结果显示,肺肿瘤模型周围的磁感应强度比正常人大10.52%。

图10正常人与肺肿瘤患者模型外部磁感应强度对比
Fig10Comparisonofextemalmagneticinductionintensitybetweennormalhumanandpatientwithlungcancer
5 结语
本研究针对磁探测电阻抗成像的正问题,首先,基于LIDC数据库人体胸腔CT图像对胸腔结构进行特异性分析,并基于灰度阈值分割算法提取胸腔内部组织器官空间结构分布。依据在CT图像中提取到的先验信息并结合各组织的电学属性对胸部进行三维建模。其次,采用有限元分析方法分别计算胸腔模型的电势分布、电流密度分布、外部磁感应强度分布。在此基础上,对癌症患者和正常人外部磁感应强度数据进行对比分析,其结果显示肺肿瘤模型周围的磁感应强度比正常人大10.52%。
磁探测电阻抗成像通过向成像体注入安全激励电流激发外部磁场,成像体内部电导率分布影响电流密度分布,基于Biot-Savart定律,电流密度决定感应磁场。然而,肺部疾病会直接导致组织器官的电导率、胸腔结构等与正常人存在差异,进而引起胸部周围磁感应强度的波动异常。
外部磁场能够反映成像体内部电导率的分布,本研究提供了磁探测电阻抗成像正问题的计算方法,同时,通过对正常人与肺部肿瘤患者的数值计算分析发现其外部磁场的差异性,在一定程度上为磁探测电阻抗应用于肺部疾病检测的可行性提供重要依据。
