g-方差,g-协方差与生成元g之间的关系
2018-10-18刘览
刘 览
(徐州工程学院 数学与物理科学学院,江苏 徐州 221008)
1 引言
给定正常数 T∈(0,∞),设(Ω,F,P)是一个完备的概率空间,(Bt)t≥0是此空间上的d-维布朗运动,(Ft)t≥0是该布朗运动产生的自然σ域流,即有
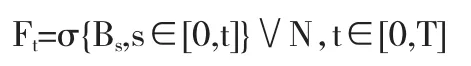
其中N是以概率测度P为可略集组成的子集类.本文限定在概率空间(Ω,FT,P)中研究问题.令 L2(Ω,FT,P)表示 FT-可测且满足:=E[|ξ|2]<+∞ 的实值随机变量 ξ全体.令 s2(0,T;R)表示循序可测且满足
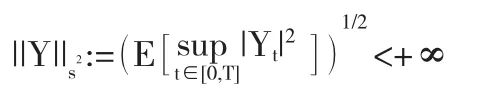
的连续实值随机过程(Yt)t∈[0,T]全体.令M2(0,T;Rd)表示Rd-值,(Ft)-循序可测且满足

的随机过程(Zt)t∈[0,T]全体.
1990年,我国著名数学家彭实戈与法国著名数学家Pardoux提出了倒向随机微分方程(简写为BSDE)的非线性形式(见文献[1]).一维BSDE的一般形式如下:
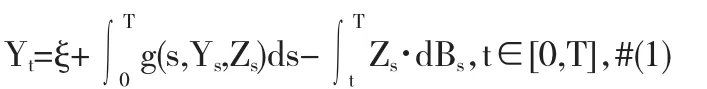
其中终端时间T有限;终端条件ξ是FT-可测的;对任意的(y,z)∈R×Rd,生成元
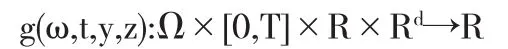
是(Ft)-循序可测的.(g,T,ξ)称为BSDE的参数.文献[1]在生成元g关于y和z一致Lipschitz连续条件下得到了BSDE的唯一平方可积适应解,记为(Yt(g,T,ξ),Zt(g,T,ξ))t∈[0,T].如果对于任意的(t,y)∈[0,T)×R,生成元g还满足g(t,y,0)≡0,文献[2]将 Y0(g,T,ξ)定义为随机变量 ξ的 g- 期望,记为 εg[ξ].g- 期望实际上是一种动态的非线性期望,它具有除了线性之外几乎所有的经典数学期望所具有的性质.文献[3]通过g-期望和条件g-期望诱导出一种风险度量和一种动态风险度量,将g-期望引入到风险度量领域.现在g-期望理论已经被许多学者所接受并被广泛应用于经济、金融、微分几何等领域.在众多学者的努力下,BSDE理论逐步完善,形成了g-概率,g-方差,g-鞅,g-估价等在内的一整套体系,并随着研究的深入不断发展.
很多学者为了完善g-期望的性质,研究了诸如Hölder不等式,Jensen不等式以及收敛性等性质,如[4],[5],[6],[7],[8],[9]和[10]等.文献[11]另辟径溪,从生成元 g 的角度出发,根据g的性质研究g-期望的性质,同时验证了g-期望和生成元g之间存在一些等价关系,从而使得g-期望的应用更加广泛.文献[11]论证了生成元g和g-期望之间很多等价性质,如齐次性,次可加性,超可加性,平移不变性等,详细研究了g-期望与风险度量之间的关系并利用g-期望量化金融头寸的风险.目前,对g-方差的理论研究则刚起步不久,[12]基于经典期望的概念定义了g-方差,研究了g-方差的一些基本性质.之后[13]又定义了g-方协差的概念,并研究了相关性质.
受[11]和[12]的启发,在本文中我们主要根据g-期望的基本性质研究g-方差和g-协方差之间的关系,以及二者和BSDE的生成元g之间的一些等价关系.由于g-期望不具有线性性,所以g-方差与g-协方差之间的关系并不像经典方差和经典协方差之间存在等式关系.此外,由[11]的结果可知生成元g的性质直接影响g-期望的性质,因此生成元g的性质也会影响到g-方差和g-协方差的性质.
本文结构如下:第2节主要介绍一些相关定义和引理;第3节主要研究g-方差与g-协方差之间的关系;第4节主要研究g-方差,g-协方差与BSDE生成元g之间的一些等价关系.
2 预备知识
对于BSDE(1)的生成元g(ω,t,y,z),考虑如下假设条件:
(A1)生成元g关于y和z满足一致Lipschitz条件,即存在常数k≥0,使得dP×dt-a.s.,对于任意的 y1,y2∈R,z1,z2∈Rd,有|g(t,y1,z1)-g(t,y2,z2)|≤K(|y1-y2|+|z1-z2|);
(A2)dP×dt-a.s.,对于任意的 y∈R,g(t,y,0)≡0;
根据[1]的结果,我们可以知道如果生成元g满足假设(A1)和(A3),那么对于任意的 ξ∈L2(Ω,FT,P),BSDE(1)在空间S2(0,T;R)×M2(0,T;Rd)中存在唯一适应解(Yt(g,T,ξ),Zt(g,T,ξ))t∈[0,T].此时需注意,假设(A2)可以推出假设(A3).因此,如果生成元g满足假设(A1)和(A2),对于任意的 ξ∈L2(Ω,FT,P),BSDE(1)在空间S2(0,T;R)×M2(0,T;Rd)中仍存在唯一解.
文献[2]利用倒向随机微分方程理论引出了g-期望的概念并详细介绍了其相关性质,现归纳如下.
定义1设生成元g满足假设(A1)与(A2),对于任意的ξ∈L2(Ω,FT,P),BSDE(1)在 S2(0,T;R)×M2(0,T;Rd)中有唯一解(Yt(g,T,ξ),Zt(g,T,ξ))t∈[0,T].定义 g- 期望 εg[·]L2(Ω,FT,P)→R 如下
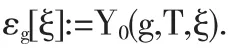
下面我们介绍g-期望的相关性质.
定理2([2])g-期望有如下基本性质:
(ⅰ)(保常性):对于任意常数 c∈R,有 εg[c]:=c;
(ⅱ)(单调性):如果 X1,X2∈L2(Ω,FT,P),X1≥X2a.s.,则 εg[X1]≥εg[X2].
注3 根据g-期望的定义,我们可以得到,当生成元g≡0 时,εg[·]=E[·].
定理4(平移不变性,[11]) 设生成元g满足假设(A1)和(A2),则如下叙述等价:
(ⅰ)不依赖 y;
(ⅱ)对于任意 X∈L2(Ω,FT,P),c∈R,有 εg(X+c)=εg(X)+c.
定理5(次(超)可加性,[11]) 设生成元g满足假设(A1)和(A2),则如下叙述等价:
(ⅰ)g不依赖于y且g关于z是次(超)可加的;
(ⅱ)g- 期望 εg[·]是次(超)可加的.
定理6(齐次性,[11]) 设生成元g满足假设(A1)和(A2),则如下叙述等价:
(ⅰ)关于(y,z)满足齐次性(正齐次性);
(ⅱ)g- 期望 εg[·]满足齐次性(正齐次性).
注7([7]) 如果g关于(y,z)满足超(次)齐次性,g-期望εg[·]也满足超(次)齐次性.
下面我们介绍[12]和[13]给出的g-方差和g-协方差的定义.
定义 8(g-方差) 对任意X∈L4(Ω,FT,P),如果εg[(X-εg(X)2]存在,则称εg[(X-εg(X)2]为随机变量X关于生成元g的g-方差,记为Varg(X).
定义 9(g-协方差) 对任意X,Y∈L4(Ω,FT,P),称 εg[(X-εg(X)(Y-εg(Y)]为随机变量X和Y关于生成元g的g-协方差,记为Covg(X,Y).
注10 由注3可知,如果生成元g=0,此时的g-方差就是经典方差,即Varg(·)=Var(·);g-协方差即为经典协方差.
3 g-方差与g-协方差之间的关系
在经典方差理论中,我们知道经典方差和经典协方差之间的关系如下,
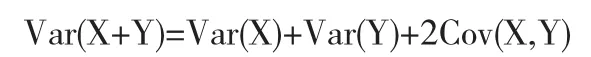
那么对于由不满足线性的g-期望诱导出来的g-方差是否有类似的等式
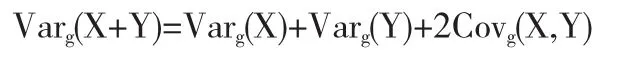
成立呢?如果不存在上述相等关系,那么g-方差和g-协方差之间到底存在何种关系呢?
由于g-期望不具有线性性,一般来说g-方差与g-协方差之间应该不具有类似的关系式,即一般来说,
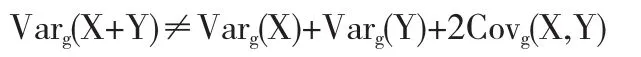
下面我们着手研究g-方差与g-协方差之间的具体关系.
定理11设生成元g不依赖于y且关于z是正齐次和次可加的,则对于任意的X,Y∈L4(Ω,FT,P),有

证明由于生成元g不依赖于y且关于z是正齐次和次可加的,根据定理4,5和6,g-期望εg[·]满足正齐次性,次可加性和平移不变性.根据g-方差的定义,有

由g-期望的正齐次性和次可加性可得,

由于g-期望具有次可加性,故

再根据g-方差,g-协方差的定义以及g-期望的正齐次性、平移不变性可得,
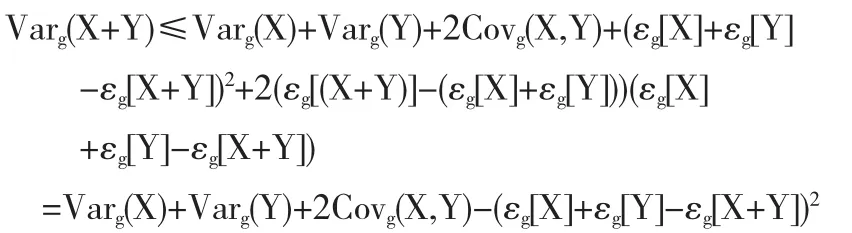
从而得出结论,

证毕.
注12 定理11中生成元g的条件可以改为,g不依赖于y且关于z是次可加和次齐次的,即对于任意的λ∈R,g(t,λz)≤λg(t,z)dP×dt-a.s.事实上,由g关于z是次可加和次齐次可以得到g关于z是正齐次的.
类似地,我们可以得到如下定理13.
定理13设生成元g不依赖于y且关于z是超齐次和超可加的,则对于任意的X,Y∈L4(Ω,FT,P),有
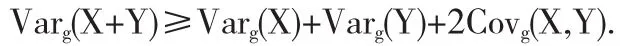
证明由于生成元g不依赖于y且关于z是超齐次和超可加的,根据定理4,5和注7,g-期望εg[·]满足超齐次性,超可加性和平移不变性.根据(2)式和超可加性可得,
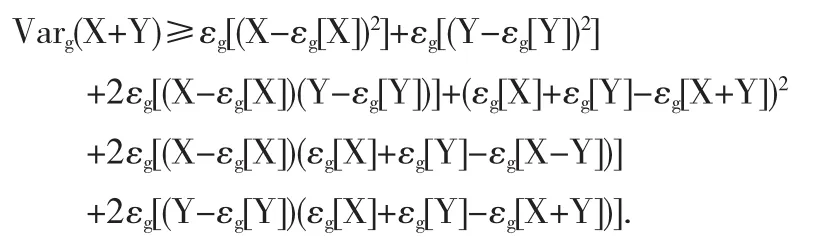
由于g-期望具有超齐次性和平移不变性,故
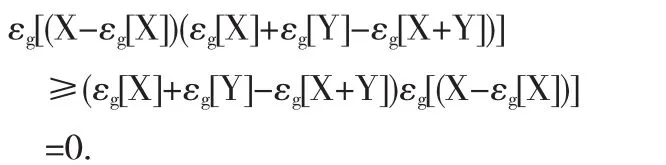
同理可得,
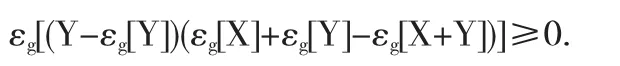
将上述两个不等式代入(3),再根据g-方差,g-协方差的定义可得,
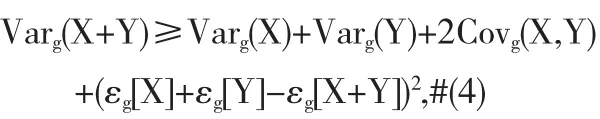
从而得出结论,
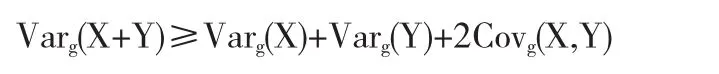
证毕.
4 g-方差,g-协方差与生成元g之间的关系
我们在研究g-方差的性质时,依赖于生成元g的性质,因为g的性质直接影响g-期望的性质,从而间接影响g-方差的性质.文献[11]通过g的性质研究g-期望的性质时,得到了很多等价的性质,即生成元g不仅可以影响g-期望的性质,反过来,g-方差的性质应该也可以影响生成元g的性质,二者之间存在哪些具体关系呢?根据定理11,借助于g-协方差我们可以得到g-方差Varg(·)与生成元g之间的等价关系.
定理14设生成元g不依赖于y且关于z是正齐次和次可加的,有

成立的充分必要条件为g是线性的.
证明首先,充分性是显然的.如果g是线性的,则g-期望εg[·]是线性的,从而很容易得到(5)成立.下面证明必要性.根据定理11的证明过程,可以得到,对于任意的X,Y∈L4(Ω,FT,P),
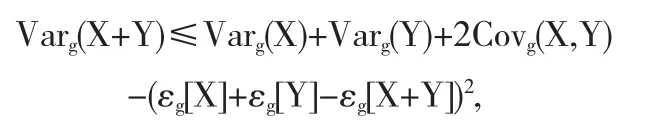
由于(5)成立,可以得出

从而对于 g- 期望 εg[·]有
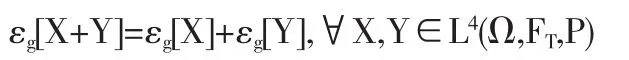
由于g不依赖于y且关于z是正齐次和次可加的,从而g是次线性的.由(6)可知g-期望是超可加的,根据定理5可得g是超可加的,于是生成元g是线性的.证毕.
类似于定理14,我们还可以得到如下定理.
定理15设生成元g不依赖于y且关于z是超齐次和超可加的,
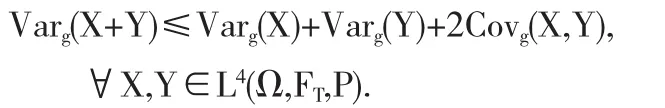
成立的充分必要条件为g是线性的.
证明充分性是显然的.如果g是线性的,则g-期望εg[·]是线性的.
对于必要性.根据定理13证明过程中的(4),可以得到,
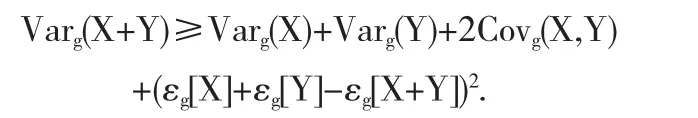
根据已知条件可以得出
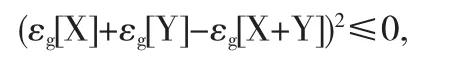
从而对于 g- 期望 εg[·]有
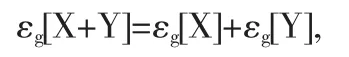
于是生成元g是线性的.证毕.
