矿井NLOS环境下改进UKF超宽带定位算法
2018-10-18李旭虹张同丽张育芝
李旭虹,张同丽,张育芝
(西安科技大学 通信与信息工程学院,陕西 西安 710054)
0 引 言
近些年,无线传感定位技术在生活中、军事上等很多方面都起着非常重要的作用,比如,地图导航、灾难救援、精确制导等都要运用定位技术。在有阻碍物阻挡的环境下对未知节点的定位和跟踪,与视距环境下的定位有很大不同,视距环境下无需考虑障碍物的影响。所以,NLOS(non line of sight,非视距)环境下的定位和跟踪,需要更高的技术要求[1]。因为矿井下的地理环境与地面有很大不同,所以传统的地面定位方案不适用于井下的应用。UWB(ultra wideband,超宽带)无线定位技术凭借着其硬件设备简单、抗多径衰落能力强、抗干扰能力强等优点,使其在井下定位的应用中得到广泛的关注[2]。
在各类无线传感网络定位系统中,运用的基本定位方法和技术都是大同小异的,对移动台的定位是通过传感器检测信号的到达角度、到达时间差等特征值来实现的。目前已有许多方法来解决NLOS问题,这些方法大致可以分为2类:静态定位分析的方法和移动跟踪分析的方法。参考文献[3]针对NLOS环境下静态定位问题总结了几种常用的方法。因为这些方法无法利用时间序列的冗余测量信息,所以在移动跟踪系统中定位效果并不十分明显。文献[4-5]利用卡尔曼滤波技术实现移动跟踪,并减小了NLOS误差的影响。文献[6]对于移动目标的定位跟踪使用了交互式多模型粒子滤波器,由于该算法计算量很大,在一定程度上影响跟踪的实时性。文献[7]在RSSI(Received Signal Strength Indication,接收信号强度)算法基础上将EKF(Extended Kalman Filter,扩展卡尔曼滤波)应用到无线定位技术中。但是EKF在线性化过程中,由于它舍去高阶项和对微小量的近似使其会引入较大的舍入误差[8]。
文中针对矿井下巷道NLOS环境较多无法进行精确定位的问题,提出基于RSSI的测距模型对传感器节点进行测距。利用三边测量定位算法根据测距结果进行初始定位,用初始定位的坐标作为UKF(unscented Kalman filter,无迹卡尔曼滤波)的观测量,并对UKF的测量更新方程进行修正,以获得较高的跟踪定位精度。此算法不需要对NLOS进行统计和鉴别,并且计算复杂度与EKF相比也大大的降低了[9]。
1 初始定位过程分析
1.1 RSSI测距
RSSI测距技术对硬件要求简单,并且能够充分利用超宽带抗多径衰落和抗干扰能力强的特点[10]。要得到目标节点二维空间的坐标,至少需要3个参考节点进行测量。由于阻碍物的阻挡信号是以反射的形式到达传感节点,所以NLOS条件下信号的传播路径相比LOS(line of sight,视距)条件下要长。在进行人员的RSSI测距估计时会受到NLOS的影响,产生一个均值为正的误差。该误差引起的超量延时如图1.图为矿井NLOS环境下RSSI对目标节点的测距估计,在LOS环境下目标节点应为测距圆的交点,而NLOS下目标节点是在测距圆的重叠区内且节点坐标与A,B,C 3点的距离之和应为最小[11]。

图1 信号强度RSSI定位估计Fig.1 RSSI location estimation
RSSI是最简单、最基础的测距方法之一,一般不需要借助额外的硬件设备,并且实现方法简单,在能量有限的节点定位中是非常重要的[12]。在基于接收信号强度的测距模型中,根据发射节点信号强度和接收节点信号强度得出信号传播的路径损耗模型为[13]
P(d)=P(d0)+10ηlog10(d/d0)+Xσ
(1)
式中d为发未知节点与参考节点之间的未知距离,m;p(d)为经过距离d后的路径损耗,db;η为信道衰减指数,该值是由矿井下实际测量得到,非视距环境越复杂,d0值越大;d0为参考距离,一般取值为1 m;Xσ为噪声变量并且服从均值为0,标准差为δ的高斯分布,标准差的取值一般为4~10.
根据(1)式可得未知节点处接收到的RSSI值为[14]
(2)
式中P为发射功率,db;G为天线增益。
假设di处未知节点的RSSI值为Pi,则根据式(2)推导出
(3)
信号在传播时,会受到噪声以及障碍物的干扰,所以实际测试距离会比di大[15]。未知节点到传感节点的距离越近,RSSI模型的距离估计误差就越小。在定位过程中,未知节点可能会收到多个信源的信号,所以应优先选择RSSI值大的信源信号进行测距计算[16]。
1.2 三边算法位置估计
三边算法是通过公式(3)计算得到的未知节点与参考节点之间的距离,通过参考节点的位置坐标来计算未知节点的位置坐标[17]。假设未知节点范围内有3个参考节点,其位置坐标分别为(xa,xa)T,(xb,xb)T, (xc,xc)T,利用RSSI测距模型计算得到参考节点与未知节点间的距离分别为da,db,dc,假设未知节点的初始定位坐标为(x,y),则有如下公式
(4)
计算式(4)可得到未知节点的初始坐标向量为
(5)
2 减小NLOS影响的UKF精确定位算法
公式(5)已经得到的未知节点的初始定位坐标,根据NLOS环境特性修正UKF算法来进行精确定位及位置跟踪。
UKF是一种新型的非线性滤波估计算法,是以UT(Unscented,无味变换)为基础的[18]。在对非线性函数进行线性化的问题上UKF与EKF的做法是不同的,UKF使用UT变换来处理均值和协方差的非线性传递,并且是直接使用系统的非线性模型。而EKF是对非线性函数进行近似而且需要计算雅可比矩阵,大大增加了计算量。UKF算法通过产生Sigma点得到更多的观测假设值,并且没有线性化的忽略高阶项,因此在NLOS环境下的非线性问题上,UKF比EKF的计算精度高,适应性更强[19]。对于非视距环境下离散时间非线性系统,其状态方程和量测方程分别为
xk+1=fk(xk)+wk
(6)
zk=hk(xk)+vk+nk
(7)

(8)

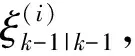
状态预测
(9)
量测预测
(10)
更新
(11)
在LOS环境下,只有测量的误差,并且该误差通常认为服从高斯分布,因此,在LOS下可以得出最优估计结果[23]。但在NLOS环境下,tk时刻的滤波值会有Kk倍的错误修正,从而使滤波后的值偏离真实状态,甚至使UKF发散。假设NLOS误差服从指数分布[24],数学模型如下
(12)
式中τrms=T1dξ,d为未知节点与参考节点之间的距离,m;T1为d处的时延扩展的中值;ξ为服从对数正态分布的随机变量[25]。
文中针对这种情况对无迹卡尔曼滤波器的更新方程进行修正,修正如下
(13)
该方法的NLOS误差,在更新方程中直接减去,使误差不会进入到下一次迭代方程中,避免UKF滤波的发散。
3 仿真结果
假设未知节点在定位过程中能收到3个基站的信号,且基站坐标分别为(0 m,0 m)、(250 m,433 m)、(500 m,0 m)。位置节点的真实坐标为X(100 m,0 m),通过RSSI测距模型得到未知节点到每个基站间的距离,再用三边测量法初步计算未知节点的初始位置坐标为X0(86.6 m,-9.7 m),将该初始的定位坐标作为UKF滤波的初值。
设UKF算法的初始状态误差协方差P=5,过程噪声协方差Q=10,观测噪声方差R=1.在matlab环境下对未知节点进行精确定位及跟踪,并与EKF滤波进行比较。
图2,图3分别给出了未知节点在随时间运动的过程中UKF和EKF 2种算法估计的坐标状态轨迹,从图中可以看出UKF滤波估计算法估计的节点坐标在真实位置附近,而EKF的波动较大。使用文中的修正误差算法后,定位性能逼近无NLOS的状态。
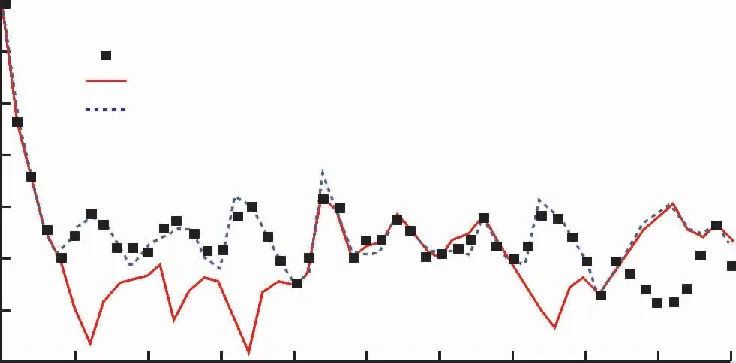
图2 X方向轨迹Fig.2 X direction trail
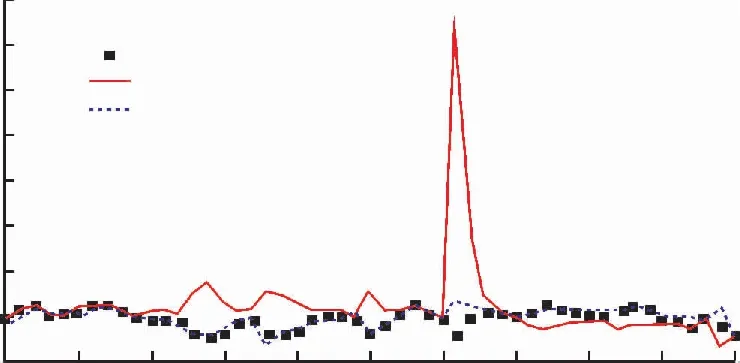
图3 Y方向轨迹Fig.3 Y direction trail
节点定位误差表达式为
errorx=|x-xk|
(14)
errory=|y-yk|
(15)
式中x,y是未知节点真实的横纵坐标;xk,yk是时刻k节点定位估计的横纵坐标。2种算法的定位误差如图4,图5所示,通过对比图可以看出,由于UKF没有忽略高阶项,与EKF相比计算复杂度不高,所以估计误差明显比EKF算法的小。

图4 X方向定位误差Fig.4 X direction positioning error
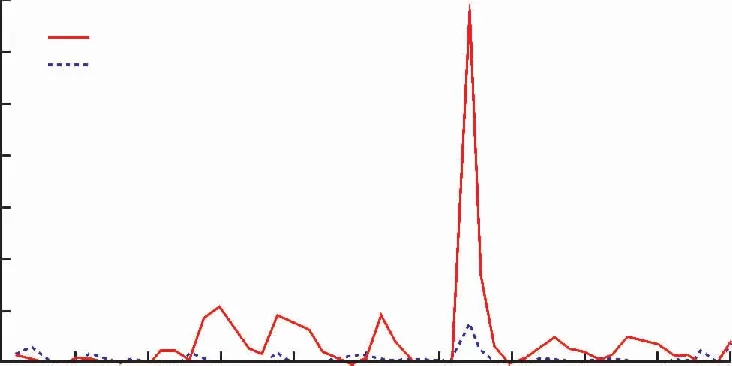
图5 Y方向定位误差Fig.5 Y direction positioning error
4 结 论
1)矿井下巷道空间有限且存在弯曲,因此通信传播大多为非视距传播环境,这种条件下采用传统的RSSI测距算法会出现较大的估计误差;
2)利用无迹卡尔曼滤波的非线性特性,在一定程度上降低了计算量,同时在它的更新阶段对滤波器进行Kk倍的错误修正,避免误差进入下一步的迭代中;
3)基于修正的无迹卡尔曼滤波的非线性定位估计算法与扩展卡尔曼滤波算法相比,目标节点在X和Y上运动方向的误差明显减小,且更接近真实值。
