试论初中数学教学中变式教学的运用

2018-10-18◆常煜

中国校外教育 2018年29期

◆常煜

(河北省唐山市第十二中学)

如今，我国大力提倡素质教学，各科教师也开始改变自身教学方式以及教学理念，更为注重对学生能力与素质的培养。数学教学不仅能够使学生学习数学理论知识，同时还能够培养学生逻辑思维以及推理能力，对学生未来发展与学习都起到极为重要的作用。教师在数学教学过程中可以使用变式教学法，通过不断对教学所用命题进行变化，能够加强学生对数学知识点的理解，加深学生记忆，同时培养学生逻辑思维。

一、当前数学教学中存在的问题

(一)应试教育的影响

就目前而言，大部分初中教师的教学目的依旧以提高学生成绩为主，以便学生能够在中考当中获得较为优秀的成绩，并不注重培养学生学习能力。受应试教育影响，教师往往对学生成绩较为关注，导致教师形成对优等生与差等生的区别待遇，使得班级内部数学成绩逐渐呈现两极分化的趋势。不仅如此，教师对学生成绩的注重，也容易使部分学习成绩较差的学生产生心理问题，认为自身能力不足，逐渐形成自卑心理。学生承受学习压力过大，对学生学习便会产生阻碍，使得学生数学水平无法得到提升。

(二)传统教学方式的影响

现今，大部分教师在教学过程当中依旧使用传统教学方式进行教学，教学效果不理想，对学生帮助不大。教师在授课过程中，往往单方面向学生灌输知识，不关注学生情感变化，也不注重与学生之间的互动，导致课堂气氛沉闷。这样的学习环境，容易使学生的注意力分散，无法集中在课堂学习当中。久而久之，学生积极性便会丧失，甚至会产生厌学心理，使得学生无法更为认真地学习数学知识，学生数学水平以及学习能力逐渐降低，成绩也会随之下降。

(三)学生方面的影响

相比其他学科的学习，学生学习数学的难度较大。数学是一门较为抽象的学科，需要学生拥有较为严谨的逻辑思维。然而大部分学生逻辑思维能力较为欠缺，无法快速理解抽象的数学知识，也不能将其应用于例题的解答当中。长此以往，学生便会对数学产生厌烦，加之应试教育、教师传统教学方式的双重压迫，部分学生开始放弃数学学习，数学成绩自然无法得到提升。

二、变式教学对初中学学教学的意义

(一)帮助学生熟练掌握教学内容

数学课堂的教学内容以各种概念、公式以及定理为主，教师在教学过程中也需侧重于上述方面的教学。教师应用变式教学法，能够帮助学生加深对上述课堂内容的理解与记忆。教师在教学过程中，可通过对概念进行演算或是在例题当中应用，以便学生了解概念的由来以及数量之间的关系，以便学生之后自行进行推理，使得学生能够自主建立各个公式以及定理之间的联系，培养学生的概括能力以及数学思维。不仅如此，教师通过对经典例题的变式，能够使学生更为了解公式以及定理该如何运用，教师可将变式前后的例题进行对比，使得学生能够更为深刻了解各公式与定理的应用方式以及应用过程中需要注意的问题。除此以外，学生在步入初中之前所受的教育有所不同，且其数学基础也存在差异。教师通过对教学内容不断的变式，能够使课程由易入难，使学生更为容易理解。同时，教师通过变式教学能够使班级内部数学水平较为平衡，不会出现两极分化现象。

(二)帮助学生形成优秀的思维模式

变式教学具有灵活多样的优点，教师能够令数学公式产生多种变化，从而与其他数学定理以及公式建立联系，使得学生在学习本节课程内容的同时，也接触其他数学知识以及定理。变式教学能够帮助学生建立发散性思维，通过一种公式及定理的学习，联想到其他知识点的学习。不仅丰富了教师的课堂教学内容，学生在变式过程中也从应试教育的压力中解脱出来。另外，学生在变式过程中还能够感受到数学的趣味性，令学生深入思考各数学知识点之间的联系，构建自身的数学知识体系。教师通过变式教学能够使学生勤于思考，思维模式更为灵活。

三、变式教学法在教学过程中的具体应用

(一)条件变式法

条件变式法是指教师在向学生讲解例题过程中，将题目当中给定的已知条件进行变形，使问题所呈现的方式得到变化，问题难度逐渐提高，引导学生进行思考，令学生对题型变化更为熟悉，对答题思路也有所掌握。条件变式法是教师在教授数学概念中较为常用的方式，能够有效提高课堂教学效率，帮助学生快速了解概念含义，并应用于问题的解答当中，培养学生的发散性思维。

题目一：设一元二次方程x2-ax-3=0，其中一个根为x=2，那么a的值为多少？另一个根的值为多少？

分析：该题目考察的重点是学生对一元二次方程根概念是否熟悉。该题难度不大，学生只需将给定的根代入方程当中，便可得出a=0.5。之后将a=0.5代入原式，则得出另一根的值为x=-1.5。

教师此时可将常数项系数进行更改，使得题目出题方式得到改变。

题目二：设存在一元二次方程x2-ax-b=0，其中一个根的值为x=b，且b不等于零，则此时a+b的值为多少？

该题目考察的重点依旧是学生对一元二次方程根概念是否熟悉。但是条件却与题目一不同，难度也有所增加。学生需对求根公式较为熟悉方能解答。教师此时可继续变形，令学生对概念的掌握更为熟练。

题目三的解题方式较为复杂，学生若要进行解答，不仅需要掌握根的求值公式，同时还应熟悉等值变形，方能解答该题目。

(二)问题变式法

条件变式法是指教师在向学生教学过程中，将例题题目当中给定的问题进行变形。通过不同的问题，使学生能够灵活运用自身所学知识，同时引导学生运用多种角度对问题进行探索，提高学生思维灵活度，使学生熟练掌握解题思路以及技巧。

题目四：设圆内存在内接三角形△ABC(如图1所示)，其中AD为内接三角形△ABC的高，AE则为圆的直径，点O为原点。请证明：AB·AC=AE·AD。

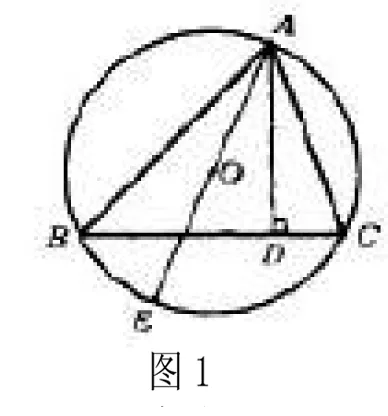
分析：该题的主要考察方向为相似三角形的相关性质，但学生还应了解圆的相关定义。具体解法如下：

教师在引导学生解决题目四之后，可对题目问题进行以下几种变化：第一种，设AD为内接三角形△ABC的高，BC、AE皆为圆的直径，连接BE(如图2所示)。则图中共有多少个三角形与△ABC相似？第二种，设AD为内接三角形△ABC的高，AE为圆的直径(如图2所示)，其中AB值为4，AC值为3，AD值为2，则此时圆的面积是多少？第三种，设AD为内接三角形△ABC的高，AE为圆的直径(如图2所示)，其中AB值为10，AD值为8，则此时cot∠CAE值为多少？