德拜媒质微波加热过程的H∞保性能温度跟踪控制

钟佳岐 梁山 熊庆宇

过去20年,微波加热已经广泛应用于食品加工[1]、化工合成[2]、物料干燥[3]以及陶瓷烧结[4]等各个领域并取得了长足的发展.作为一种典型的体积加热模式,相比于传统的加热方法,微波能极大地提升介电媒质的全局温升速率.但是,电磁场的传播特性以及时变介电特性必然会导致在加热过程中热点的产生,若缺乏合理的功率调节策略,将有可能导致燃烧爆炸等一系列危险性事故[5].针对该问题,不少学者已经从不同观点出发,研究抑制热失控的方法[6−8],但由于电磁场环境中的在线温度检测技术极不成熟,导致难以完全依赖输入输出信息,设计合理的调控策略.因此,需要基于微波加热机理模型,提出一种全新的温度跟踪控制策略,实现热失控的抑制,保证微波能应用的安全性、高效性以及可靠性.

由于多物理场自身演化与相互耦合的特征,使得微波加热过程常用一组具有时空耦合特性的模型[9]进行描述,其主要包含偏微分方程(Partial differential equation,PDE),非齐次Neumann边界条件以及初始条件.就PDE方程来说,它不仅能描述媒质内部热传导特性,还能利用非齐次项耦合“热–电磁”的瞬态演化过程.然而,对于德拜媒质[10],随温度变化的介电常数将会导致电磁分布也呈现出极强时变性.虽然Akkari等[8]和Damour等[11]学者基于微波加热的PDE模型开展了多变量跟踪及温度预测等大量的工作,但仍然没有讨论随温度变化的介电特性以及输入功率的约束对微波加热整体性能的影响.近年来,尽管Yin等[12]已经在数学层面上证明了在空间中存在一个最优电场,能够使德拜媒质具有期望的温升速率,但在控制器的实现上仍然存在一定的不足.其原因是:缺乏适合微波加热控制器设计的简化模型.受此启发,Zhong等[13−14]改进谱迦辽金法,将微波加热PDE模型转化成有限维常微分方程(Ordinary differential equation,ODE)模型,提高多参量预测的速率并减小系统分析的难度,为温度控制器设计与实现奠定基础.

过去几年,输入受限的受扰系统镇定问题得到了广泛关注,诸如模型预测[15−16]、抗饱和设计[17−18]等控制方法如雨后春笋般涌现而出.对于受扰线性系统的对称输入饱和问题,Chen等[19]已经进行了充分研究,将H∞增益、耗散不等式以及不变集理论进行融合,有效地处理了较高性能需求与饱和约束间的关系.然而,单一的H∞性能指标仅能保证系统稳定性与抗干扰性能,并不能完全满足多目标性能优化的要求.受此启发,很多学者近年来针对H∞增益与保性能函数相融合情形下控制器的设计问题[20−21]进行研究,使闭环系统镇定的同时,达到抗干扰与保性能的需求.但在德拜媒质微波加热过程中,非齐次Neumann边界条件的扰动以及介电常数随温度变化的特性使得微波加热模型呈现出极强的时变特性.因此,围绕微波加热模型所具有的输入饱和、外部扰动以及内部不确定性等本质属性,需进一步将多目标性能函数(例如H∞范数[22]、二次型函数[23]等)融入到温度调控过程中.然而,针对具有输入饱和的不确定系统多目标控制器的设计仍缺乏足够的研究.倘若将上述控制方法用于德拜媒质微波加热过程中的热失控抑制,不仅会影响闭环动态性能,更难以保证温度调控过程中的稳定性和鲁棒性.

德拜媒质微波加热过程中的热失控抑制问题本质上是同时具有输入饱和、内部不确定性以及外部扰动特征系统的输出跟踪问题.因此,本文充分考虑以上提及的各项影响系统动态性能的因素,将输出跟踪问题转化为误差镇定问题,结合线性矩阵不等式(Linear matrix inequality,LMI)技术与滚动优化原理,提出滚动时域H∞保性能跟踪控制策略.本文提出的方法能够在线权衡系统性能需求与输入约束间的矛盾,在德拜媒质微波加热控制过程中可跟踪最高温度监测区域并抑制热失控的发生.

1 预备知识

众所周知,在微波加热过程中,全局瞬态温度分布受电磁场与热动力学场间的相互耦合作用而产生显著的变化.为了简化上述复杂的数学建模过程,本文针对非磁性德拜媒质中的主要特征,并给出如下三项假设:

假设1.被加热媒质的材质均匀且各向同性;

假设2.媒质的体积变化和质传可被忽略;

假设3.媒质的热力学特性不随温度变化但介电特性随温度变化.

基于热力学第一定律,在一维方向上的德拜媒质微波加热过程的数学模型可由下述偏微分方程模型进行描述.

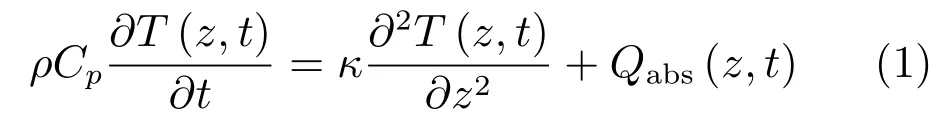
边界条件

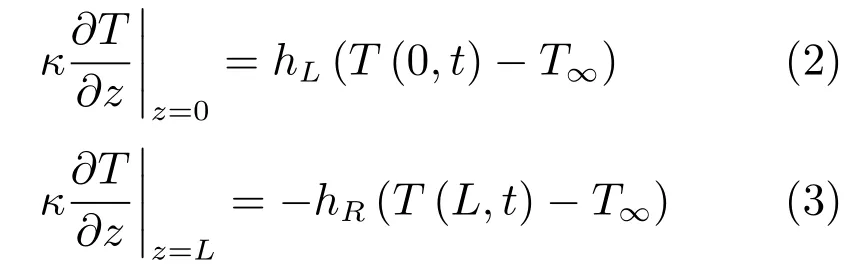
初始条件

其中,T=T(z,t)表示在t时刻及z位置的温度;ρ,Cp和κ分别表示媒质的密度、比热容及热导率;hL和hR表示在媒质边界的传热系数;T∞为环境温度,Qabs是内热源项.在微波加热领域,内热源项Qabs也被称为耗散功率.通常情况下,耗散功率同时受微波频率f、相对介电损耗∈′′(T)以及局部电场E的影响,可表示为

其中,∈0=8.854×10−14rad/cm 是真空中的电导率;E∗是局部电场的共轭复数;根据德拜方程,随温度变化的复介电常数∈(T)可由下述一阶方程进行描述[24].

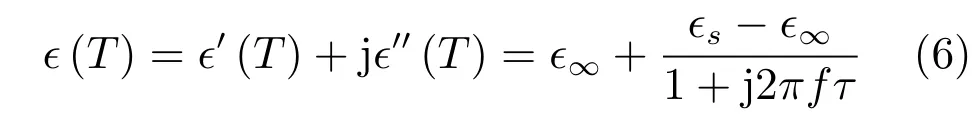
其中,∈′(T)是相对介电常数;∈∞为无限频率相对介电常数;∈s是静态相对介电常数;τ表示当电场消失后,原子回返原来状态的时间,通常将其称为弛豫时间;j为虚部符号.

从模型(1)～(4)可以看出:由于非齐次Neumann边界条件和无限维特性的约束,很难基于原始的PDE模型进行控制器设计.针对此问题,Zhong等[13]应用改进型谱迦辽金法,将原始的PDE模型进行时空分离与迦辽金截断.为了更明确地表达所提出的模型,可将入射电场强度E0从耗散功率(5)中剥离,并定义下述符号:u=|E0|2,a=hL(T(0,t)−T∞),b=−hR(T(L,t)−T∞),h(z)=(b−a)/(2L)×z2+az,k1=κ/(ρCp),k2=1/(ρCp),λi=−(iπ/L)2和φi(z)=cos(iπz/L),i=0,1,···,n,可得到时空分离的有限维ODE模型

其中,

2 滚动时域H∞温度跟踪控制

为了将跟踪问题转化为镇定问题,首先考虑有限维微波加热ODE模型(7)和模型(8)的离散时间模型

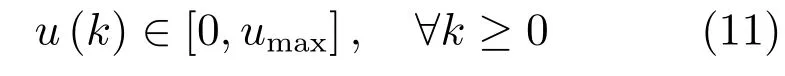
很明显,本文的控制目标是在式(11)约束下,设计H∞保性能控制器,使得监测点的最高温度能跟踪上期望温升曲线Tref(k),并且其误差可表示为

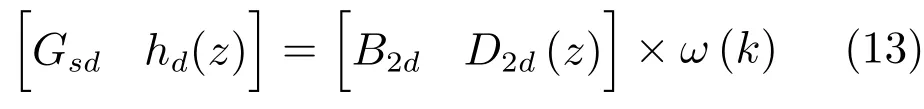
显然,可结合不同时刻离散型的状态方程、输出方程以及跟踪目标构造输出增广系统.但由于随温度变化的介电特性,必然导致耗散功率在相邻时刻内产生细微的变化.但从控制的角度来看,时变的介电特性必然会导致模型的不确定性.若k−1时刻的状态方程为

其中,∆Bsd表示相邻时刻输入矩阵的细微差别.利用式(9),(10),(12)和(14),可构造相应的增广系统

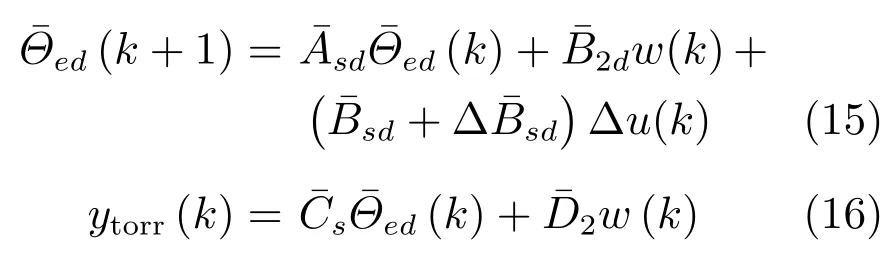
其中,

注1.上述推导过程将温度输出跟踪问题转变为增广系统的镇定问题.但需注意的是,增广系统的输出ytorr(k)主要体现跟踪性能的优劣程度.当然,它不仅与相邻时刻温度谱误差相关,而且取决于温度跟踪误差.在增广系统的输出方程中,C1为待定系数矩阵,其解析化地体现出所设计控制器对输出温度“完美”跟踪的期望程度.一般来说,C1越大,说明模型所能容忍的跟踪误差就越小,所需控制器输入幅值的震荡程度也可能会进一步增大.因此,选择合理的待定系数矩阵对闭环跟踪系统的动态性能显得尤为重要.

注2.由于原始的有限维微波加热模型受非对称的饱和特性所约束,也就是u∈[0,umax].同样的,所推导出的误差增广模型也受非对称饱和特性的约束,根据前后时刻输入约束的线性关系,不难得出误差输入的非对称饱和约束范围

接下来,将针对具有非对称约束(17)的增广模型(15)和模型(16)设计滚动时域H∞保性能控制器.换句话说,所构造的闭环增广系统不仅需要满足H∞增益,而且需要满足多目标优化函数.因此,需要基于当前时刻的误差温度谱和误差增益提出相应的保性能评价函数

其中,Q和R均是已知的对称正定矩阵.

定义1.考虑不确定增广系统(15)和系统(16),若存在一个正常数γ和一个正定矩阵P,使得[25]

定义2.考虑不确定增广系统(15)和系统(16),如果存在一个误差增益∆u∗(k)和一个正实数J∗,使得对于所有允许的不确定性,闭环增广系统是稳定的且闭环的二次评价函数(18)满足J≤J∗.那么,对于不确定增广系统(15)和系统(16)来说,J∗被称为保性能指标而∆u∗(k)则被称为保性能误差控制律[26].

其中,Dd和Ed是具有相应维数的已知实常数矩阵;F(k)是一个具有Lebesgue可测元素的未知矩阵函数,其满足下述关系:

秉持由简单到复杂的思路,利用LMI多目标优化的框架,需要围绕增广系统(15)和系统(16)构建不受输入饱和约束的H∞保性能控制器,并在此基础上推导出处理饱和特性所需的椭球体.但在给出定理之前,需要引入以下引理.

引理1.假设具有适当维数的实矩阵Ψ1和Ψ2,对于任意非零向量x∈Rn以及所有的F(k)满足式(21),使得下式成立[27]:

引理2.假设具有适当维数的对称矩阵Ψ3≥0,Ψ4≥0以及Ψ5＜0,对于任意非零向量x∈Rn,满足下述关系[28]:

则存在相应的正实数ε,使得下述不等式成立:

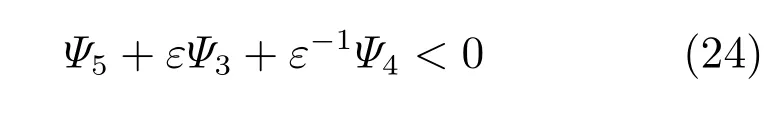
引理3(Schur补引理)[29].假设一个对称矩阵S能划分为以下四个部分:

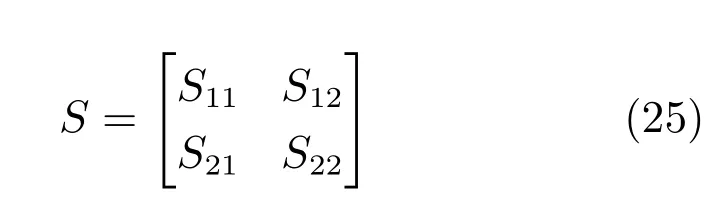
其中,S11=ST11,S22=ST22以及ST21=S12.那么,下述性质成立:

定理1.考虑不确定型增广系统(15)和系统(16)以及二次评价函数(18),如果存在对称的正定矩阵P,两个正常数γ和ε以及满足约束(21)的不确定性矩阵F(k),使得下述矩阵不等式成立:

证明.首先构建一个既满足H∞增益,又满足保性能约束的矩阵不等式条件

很明显,根据定义1,矩阵不等式(27)能够使不确定增广系统满足H∞性能指标.若将其分别左乘和右乘非零向量,可推导出下述耗散不等式:

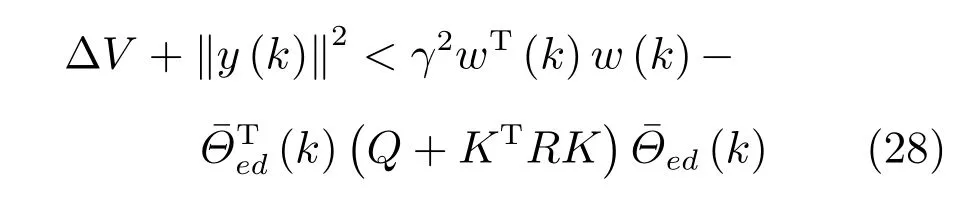
若将式(28)从k−1时刻累加到k时刻,能获得当前时刻评价函数的极大值

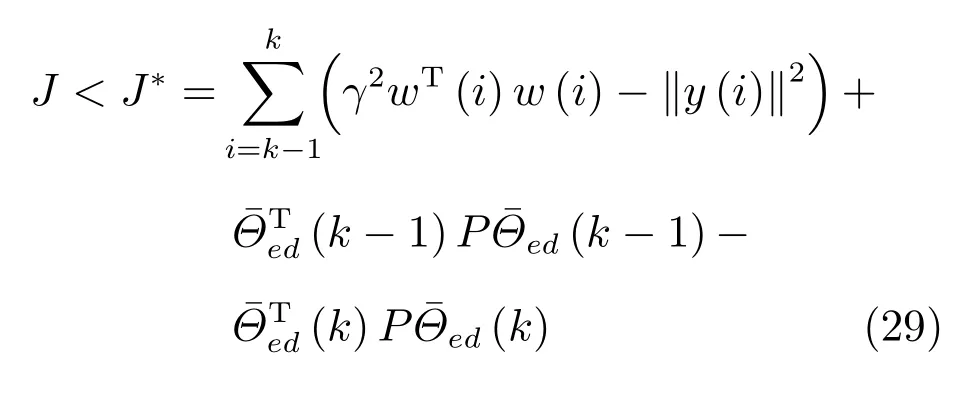
结合定义2,可明显地看出,矩阵不等式(27)同样也能满足相应的保性能评价函数(18).接下来,为了保证计算的可行性,未知矩阵函数F(k)将会被进一步消除.依次利用引理1、引理2和引理3,可将式(27)转化为

再次使用引理3,可获矩阵不等式(26). □

为了处理输入饱和约束的限制,需要构造同时满足H∞增益和保性能函数(18)下的椭球集.根据耗散不等式(28),可以得出

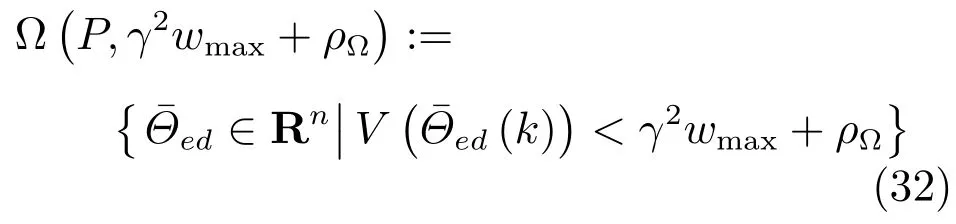
定理2.若在矩阵不等式(26)的约束下,同时存在一个正常数ρΩ,使得下述矩阵不等式成立:

那么,H∞保性能控制器满足对称饱和约束,即∆u∈[−uopduopd].

证明.椭球体可围绕过去某时刻k−1与当前时刻k的关系进行构造,利用引理3,很容易得出等价于矩阵不等式(33).利用Cauchy-Schwarz不等式,对称输入饱和与椭球体的关系可获得

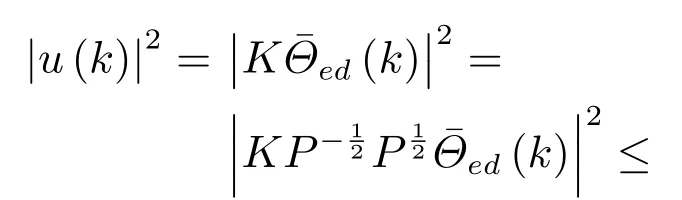
再次利用引理3,可将式(35)转化为矩阵不等式(34). □

然而,上述讨论推导出的是一组双线性矩阵不等式(Bilinear matrix inequalities,BMIs).众所周知,BMI是非凸的,并不适用于求取全局最优解.因此,需要采取一种等价变换的方法将BMI转化为线性矩阵不等式(LMI),以进一步分析相应的控制器设计的最优问题.

定理3.如果下述优化问题

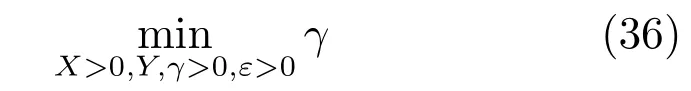
满足约束条件

存在最优解(X,Y,γ,ε).那么,对于具有滚动时域H∞保性能误差控制器的不确定闭环增广系统(15)和系统(16)存在下述性质:

性质1.对所有容许的不确定性,其内部是渐近稳定的;

性质2.其误差控制器∆u满足对称约束[−uopd,uopd];

性质3.有界外部扰动w(k)到不确定增广系统的输出ytorr(k)的H∞范数最小,其值为γ2;

性质4.保性能函数具有上界J∗,且在每一时刻,二次评价函数(18)均满足J≤J∗.

证明.为了将BMI转化为LMI,首先将矩阵不等式(26)的左侧分别左乘和右乘对称矩阵diag{P−1,I,P−1,I,εI,I,I,I},再令X=P−1和Y=KP−1,其等价的LMI形式(37)可获得.若令α=γ2wmax+ρΩ,式(33)可等价变换成

利用Schur补引理,式(38)能够获得.采用相同的方法,式(34)亦可转化成

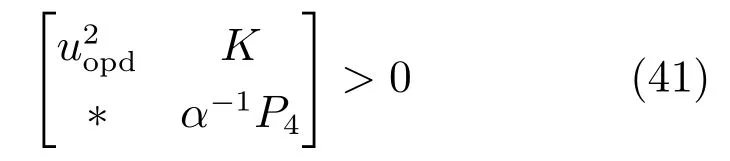
利用引理3并将矩阵不等式(41)的左边分别左乘和右乘对称矩阵diag{I,P−1},从而能获得式(39).根据定理1和定理2的相关内容,可得出闭环增广系统(15)和系统(16)满足性质1～4. □

注3.定理1和定理2是在LMI多目标优化的框架下,讨论同时存在输入饱和、外部扰动以及内部不确定性约束的H∞保性能控制器设计问题,其目的是保证闭环增广系统(15)和系统(16)在任意时刻的稳定性以及鲁棒性能.但由于在德拜媒质微波加热过程中,离线的增益难以保证输出跟踪的精准性.为解决该问题,融合滚动优化的原理,利用每一采样时刻的模型和状态更新LMI优化问题并在线求解.因此,定理3摒弃传统方法的保守性,充分利用受饱和输入约束的控制性能,实现H∞性能指标γ的在线最小化,使得闭环系统的跟踪性能在滚动时间域中达到最优.

从注3可以看出,将滚动时域的思想融入到H∞保性能控制器实现的关键则是合理选取采样周期并在线更新模型参量以及增广状态.值得指出的是,LMI条件(39)中的常实数uopd并不能充分利用有限的控制量,难以主动提高系统性能指标并实现非对称饱和约束.因此,下面给出滚动时域H∞保性能跟踪算法的具体步骤:

步骤1.选择合适的评价函数矩阵Q和R,并初始化LMIs条件(37)～(39),其中给定输入约束边界uopd=umax,初始跟踪位置^z并获取初始增广误差状态变量sd(0).

步骤2.在初始时刻k=0,选择合适的输入增益u=u0,并将其代入到离散形式的有限维微波加热ODE模型(9)和模型(10)中,然后k=k+1.

步骤3.在每一时刻k＞0,更新输入矩阵Bsd、不确定输入矩阵∆Bsd、跟踪位置、状态变量−1),并定义输入约束,接着再求解LMIs优化问题(36),获取可行集(X1,Y1,γ1,ε1).

步骤4.判定是否满足非对称约束[0,umax];若满足,将其代入到模型(9)和模型(10)中,并使k=k+1,转到步骤3;若不满足,更新约束边界uopd=|u(k−1)|2.

步骤5.重新求解LMIs优化问题(36),获取可行集,将控制器输入代入到模型(9)和模型(10)中,并使k=k+1,转到步骤3.

3 仿真实例

在本节中,上述提出的滚动时域H∞保性能跟踪控制策略将会应用于一维微波加热波导仿真模型以验证其有效性,其原理如图1所示.

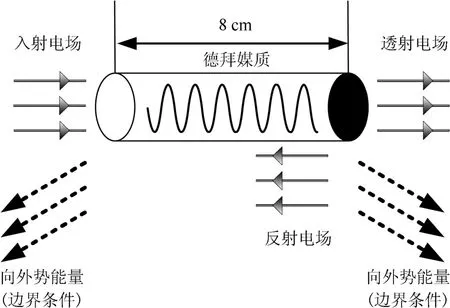
图1 微波加热德拜媒质的详细原理图Fig.1 Detailed schematic diagram for microwave heating Debye medium

正如前面所述,本次仿真将会耦合无网格化热动力学场与网格化电磁场.就热动力学场来说,媒质内部的温度升高不仅会加剧媒质内部的热传导,而且在边界处与外部环境产生向外的热对流.该类型的热对流在上述推导过程中也被称为非齐次的Neumann边界条件.相应的热动力学参数与边界条件如表1所示.

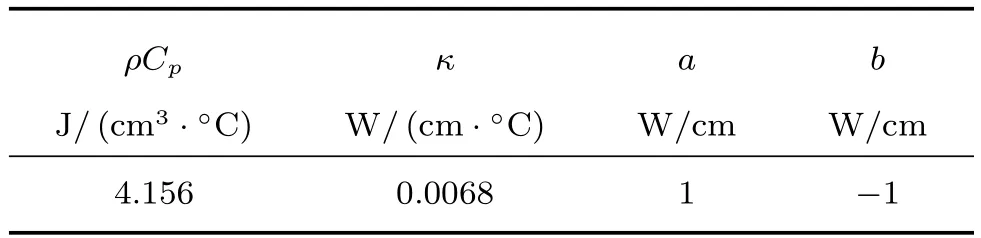
表1 热力学参数和非齐次Neumann边界条件Table 1 Thermodynamic parameters and nonhomogeneous Neumann boundary condition

对于电磁场来说,首先假设均匀的TEM 波从媒质左侧垂直入射,并且在右侧边界处发生透射及反射.由于介电特性随温度变化的特性,很难获得一个明确的耗散功率表达式.为了解决该问题,可将空间坐标均匀分成m等份,再利用时域有限差分(Finite difference time domain,FDTD) 法求解下述已简化的Helmholtz方程

图2 相对介电常数∈′(T)和相对介电损耗∈′′(T)Fig.2 Relative dielectric constant∈′(T)and relative dielectric loss∈′′(T)

接下来,结合局部电场和介电常数,局部耗散功率Qabs(zi,t),i=1,2,···,m也能获得.并利用线性拟合的思路,任意时刻的全局耗散功率Qabs(z,t)也能获得.此外,通过前面的分析与计算,能容易地获得在线输入矩阵Bs.相反,所提出的有限维ODE模型能够获得全局的温度分布以此来更新局部耗散功率.因此,所提出的电磁场和热力学场耦合模型能够用于描述图1所述的微波加热德拜媒质模型.

对于微波加热长波导模型,其热点必定会出现在离微波馈入口较近的区域.因此,可以假设6个传感器分别置于0cm,0.25cm,0.5cm,1.0cm,2.0cm和3.0cm处,旨在为在线跟踪选取合理的位置.进一步,假设模型的初始温度为20◦C,临界温度为100◦C以及期望温升曲线为

系统的输入变量u(k)(即入射电场强度E20)需满足如下饱和约束

为达到理想的跟踪效果,取C1=1,α=250,u0=100V2/cm2,Q=5×10−4I,R=1×10−4I.并将本文提出的滚动时域H∞保性能温度跟踪算法作用于运用五阶迦辽金截断的微波加热离散ODE模型,实现对监测点的最高温度进行跟踪,其结果如图3所示.从图3可以看出,所提出的跟踪控制算法能够有效地抑制有界的外部扰动和输入的不确定性.但由于该类模型自身的特点,备选跟踪位置的温度能够快速上升,并且能跟踪上期望温度.但是在恒温阶段,边界的热对流与内部的热传导效应必然会引起整体温度的下降,因此,入射电场将会始终为正,并保持跟踪位置的期望温度,如图4所示.结合图3和图4可以看出,在控制器时域硬约束的情况下,所提出的控制算法只能以牺牲动态性能为代价,以保证入射电场幅度不超过非对称饱和的临界值.进一步,同样探究了加热过程中媒质内部的全局温度分布以及保性能函数,其结果如图5和图6所示.

图3 监测点最高温度与期望温升曲线Fig.3 Maximum temperature rise curve in monitoring positions and reference temperature rise curve

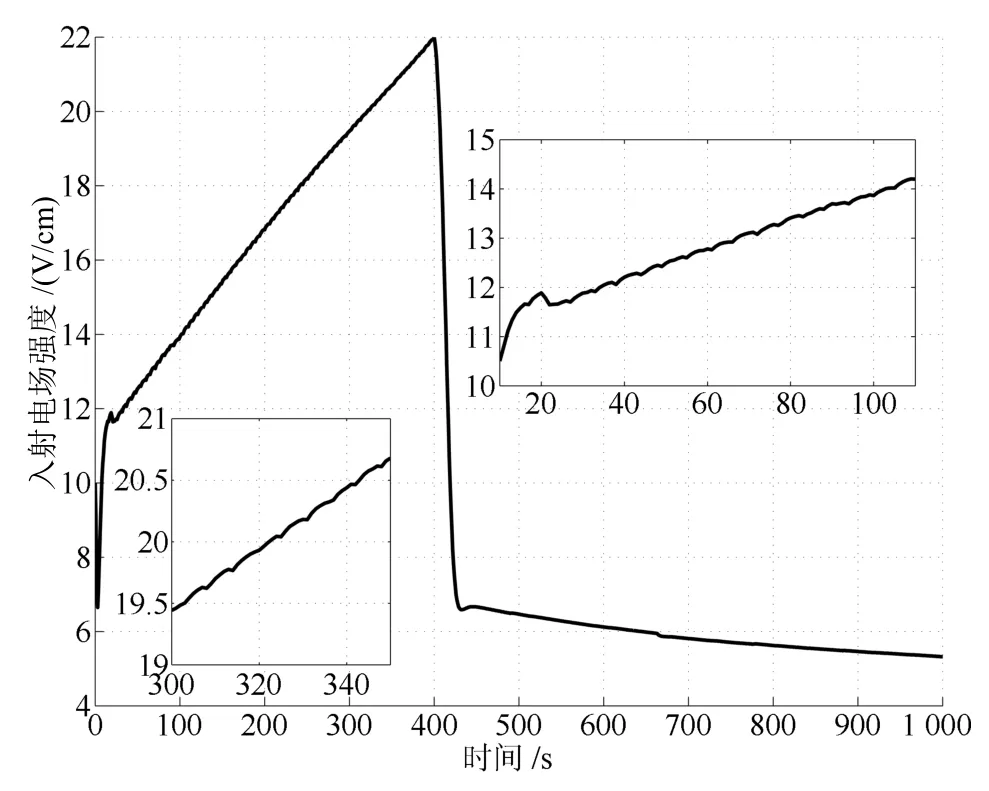
图4 入射电场强度Fig.4 Incident electric field intensity

图5 全局温度分布Fig.5 Global temperature distribution

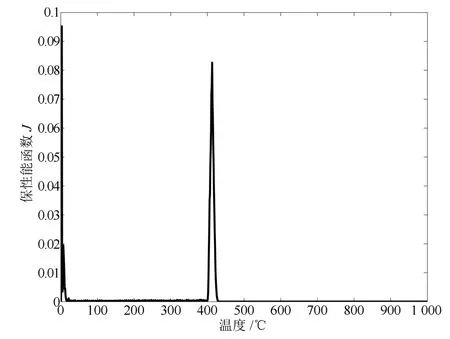
图6 保性能函数J的实际轨迹Fig.6 Actual trajectory for guaranteed cost functionJ

从图5中可以看出,在1000s以内的加热过程中,离微波馈入口越近的位置,电场强度较高,温升速率必然更快,而离微波馈入口越远的位置,温升速率则更慢.因此,通过利用最高在线温度跟踪的方法能够有效地抑制失控.此外,如图6所示,在前20s的加热过程中,需要快速地跟踪上期望温度,其入射电场增量及状态变量的波动幅度较大,从而导致保性能函数也有较大幅度的波动.而在温升过程中,虽然入射电场增量变动不大,但温度谱及温度误差仍然有所增大,也会导致保性能函数逐步增加.但到恒温阶段,由于各类误差逐步缩小,其保性能函数同样也逐步趋于0.综上所述,仿真的结果能进一步表明:所提出的H∞保性能跟踪控制器能够有效地解决微波加热德拜媒质时最高温度的跟踪问题.

4 结论

本文主要针对德拜媒质微波加热过程中热失控抑制问题,研究了基于时空耦合机理模型的输入受限鲁棒跟踪控制器的设计方法.以H∞增益和保性能函数为性能指标,在LMI多目标优化框架下,推导出满足输入受限H∞保性能跟踪控制器存在的充分条件,并给出了滚动时域跟踪控制的实现算法.通过德拜媒质微波加热短波导仿真模型验证了设计方法的有效性与可行性.