基于映射字典学习的跨模态哈希检索
2018-10-18姚涛孔祥维付海燕TIANQi
姚涛 孔祥维 付海燕 TIAN Qi
随着计算机网络和信息技术的快速发展,网络上的媒体数据量急剧增长,媒体的表示形式也呈现出多模态性(图像、文本、声音、视频等).例如:在微博上传照片时,往往会同时上传一段文字描述照片的内容或用一些标签标注图像的内容;在微信的朋友圈分享时,往往也是图文并茂;购物网站,例如淘宝、京东等,在描述产品信息时通常既用图片,又用文字.这些多模态数据虽然表现形式不同,但它们之间存在语义关联.跨媒体检索的目的就是挖掘不同媒体之间存在的语义关系,并按语义关系进行排序,返回跟查询存在较强语义关系的不同模态的数据.随着媒体数据量的急速增长和模态的多样化,传统的检索方法已经不能满足当前跨媒体检索的需求.如何在海量数据中检索不同模态的数据成为一个巨大的挑战.
哈希方法是解决大数据问题的一种有效的方法,不仅能大大节省存储空间,而且计算效率也大幅提高.例如一张图片用5000维的BOW表示,假设每维用double数据类型表示,即每维占用8Bytes的存储空间,则需要5000×8Bytes=40000Bytes的存储空间.而哈希方法是把数据映射汉明空间,例如用32bits(8bits=1Byte)来表示一张图片,仅需要4Bytes的存储空间,大大节省了存储空间,占用的存储空间仅为原始特征空间的万分之一.在检索过程中,因为数据用二值码表示,因此在计算样本间的距离时,只需要做简单的异或操作即可,大大提升了计算的效率,使检索的时间复杂度远低于传统方法.
针对以上问题,本文提出一种基于映射字典学习的跨媒体哈希算法,主要贡献如下:
1)利用映射字典学习使哈希码含有语义信息以提升算法的性能.算法同时学习了哈希函数,这与现存的字典学习哈希算法不同.
2)提出通过最小化量化误差,学习一个正交旋转矩阵,提升算法的性能,并且可以证明旋转后的解依然是问题的局部最优解.
本文结构安排如下:第1节介绍哈希算法的相关工作;第2节回顾字典学习的相关内容,阐述了本文算法的思想,优化过程及计算复杂度分析;第3节给出在两个公开数据集上的实验结果;第4节对本文的研究内容进行总结.
1 相关工作
由于哈希方法的高效性和节省内存,最近引起了越来越多的关注[1−15].哈希方法一般可以分为单模态哈希和多模态哈希.
单模态哈希方法又可以分为不依赖数据的哈希方法和依赖数据的哈希方法.在不依赖数据的哈希方法中,最先提出的是局部敏感哈希(Local sensitive hashing,LSH),它利用随机线性映射作为哈希函数,把原始空间中的样本映射到汉明空间[1].但是,样本之间的相似性是非线性的,线性函数很难捕捉样本之间的内在联系,因此核局部敏感哈希(Kernelized local sensitive hashing,KLSH)提出利用核方法捕捉样本之间的内在联系[2].但是,这类算法往往需要很长的哈希码和多个哈希表才能取得较好的实验结果.然而随着哈希码长度的增加,会降低相似样本映射到同一个桶的概率,导致召回率的迅速降低,而且较长的哈希码必然会增加存储空间和计算复杂度.相对于不依赖于数据的哈希方法,依赖于数据的哈希方法可以获得更为紧凑的表示,较小的码长就可以获得令人满意的结果,因此受到越来越多的研究人员关注[4−8].谱哈希(Spectral hashing,SH)通过放松哈希函数的二值约束,利用谱图分析和拉普拉斯特征函数学习哈希函数[4].核监督哈希(Supervised hashing with kernels,KSH)利用核方法学习哈希函数,在汉明空间最小化正样本对之间的距离,最大化负样本对的距离[5].以上算法取得较好的实验结果,但是没有考虑量化损失的影响,导致学习到的哈希函数的性能的下降.迭代量化哈希(Iterative quantization,ITQ)通过最小化量化误差,学习一个旋转矩阵,得到性能更好的哈希函数[6].监督离散哈希(Supervised discrete hashing,SDH)提出了一种离散优化算法,直接可以得到问题的离散局部最优解[7].然而随着网络上多模态数据的不断增长,一个网页可以包含多种模态的数据,而单模态的哈希方法通常不能直接用于多模态数据,如何把多模态数据纳入到一个统一的学习框架成为新的挑战.
多模态哈希方法一般分为多模态融合哈希方法和跨模态哈希方法,本文主要研究跨模态哈希方法.多模态融合哈希方法利用不同特征之间的互补性,学习一个更好的汉明空间,提升算法的性能[8−10].跨模态哈希的目标是学习一个共享的汉明空间,在这个空间可以实现跨媒体检索[6,11−17].基于相似敏感哈希的跨模态度量学习方法(Cross-modality metric learning using similarity sensitive hashing,CMSSH)通过最小化不同模态的相似样本之间的汉明距离,最大化不同模态的不相似样本间的汉明距离,学习哈希函数[11].典型相关分析(Canonical correlation analysis,CCA)[18]哈希方法,把CCA引入跨媒体哈希方法,提出最大化模态间的相关性,学习一组哈希函数[6].然而上述方法只保持了模态间的相似性,忽视了模态内的相似性.跨视角哈希(Cross view hashing,CVH)把谱哈希扩展到跨模态检索,通过最小化加权距离,保持相似样本(模态内和模态间)的相似性[12].多模态潜在二值嵌入(Multi-modal latent binary embedding,MLBE)提出一个概率生成模型,通过保持多模态样本的模态内和模态间的相似度来学习哈希函数[16].然而,这些方法并没有为不同模态的数据学习一个统一特征空间,导致无法捕捉不同模态间存在的一些潜在的共享信息.协同矩阵分解哈希(Collective matrix factorization hashing,CMFH)利用协同矩阵分解保持模态间的相似性,为样本对学习同一表示[13].基于聚类联合矩阵分解哈希(Cluster-based joint matrix factorization hashing,CJMFH)提出了首先对各个模态进行聚类运算,再利用矩阵分解同时保持模态内、模态间和基于聚类的相似性[17].以上方法虽然取得了令人满意的结果,但是学习到的哈希码不包含任何语义信息,限制了算法的性能.稀疏哈希(Latent semantic sparse hashing,LSSH)为了缩小图像和文本之间的语义鸿沟,利用稀疏表示学习图像的一些显著结构,利用矩阵分解为文本学习一个潜在的语义空间,并保持模态间的语义相似性[14].稀疏多模态哈希(Sparse multi-modal hashing,SMMH)提出利用稀疏表示为图像和文本学习一个共同的语义空间,保持模态间的相似性[15].这类方法利用稀疏表示,使哈希码包含语义信息,提升了算法的性能.但是这类算法通常存在以下问题,限制了算法的应用.1)在字典学习算法中,因为稀疏约束项的存在,导致训练和测试过程算法的复杂度高.2)这些哈希算法不同于传统的哈希算法,没有学习显式的哈希函数.测试样本,通常需要首先解决一个Lasso问题,得到样本的稀疏表示,然后通过量化得到样本的哈希码(例如文献[14]),而不能像传统算法那样直接利用哈希函数到.3)因为得到的系数矩阵是稀疏的,导致了哈希码的0和1分配不均匀.
针对以上问题,本文提出一种基于映射字典学习的哈希算法.在字典学习过程中,放松了稀疏约束项算法,不仅降低了时间复杂度和平衡了哈希码的分布,而且在字典学习过程中得到了哈希函数.对于哈希问题的求解,现存的大部分跨模态哈希算法往往采用谱松弛的方法得到连续的最优解[11,19],没有考虑量化损失对算法性能的影响,而导致性能的下降[3].本文受ITQ的启发,通过最小化量化误差,学习一个正交的旋转矩阵,进一步提升算法的性能.
2 映射字典学习哈希算法(DPLH)
本节首先介绍字典学习的基本内容和本文提出的基于映射字典学习的哈希算法,然后引出优化算法及正交变换的相关内容,最后分析算法的时间复杂度,证明算法的高效性.
2.1 映射字典学习
字典学习已经在图像处理和计算机视觉领域取得了巨大的成功[20−28].传统的字典学习可以分为综合字典学习和分析字典学习两类.综合字典学习应用在各个领域取得了令人满意的成果[21−27],而分析字典学习的研究正处在起步阶段[28].
综合字典学习的目标函数一般定义为
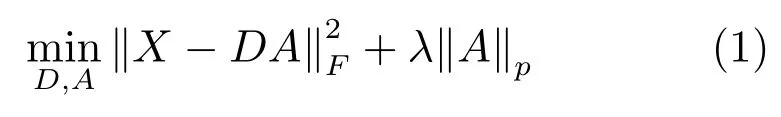
其中,X∈Rd×N表示数据,D∈Rd×c表示字典(字典的每行D(:,i)称为字典的一个原子),A∈Rc×N表示系数矩阵,λ为权重参数,‖·‖F表示Frobenius范数,一般情况下取p=1,即l1范数.式(1)表明数据X可以由字典和稀疏的系数矩阵重构.
分析字典学习目标函数一般定义为

这里的范数可以为l1或l2范数,A为稀疏矩阵,Ω表示字典.
然而,在字典学习过程中加入l1或l2稀疏约束项,往往会导致过大的计算量.文献[27]把综合字典学习和分析字典学习纳入同一个学习框架,提出了一种基于映射字典学习的分类方法,利用线性映射代替非线性的稀疏编码,取得了令人满意的结果.受此启发,本文利用线性映射的方法来进行字典学习,以减少时间复杂度,同时把学习的线性映射作为哈希函数.映射字典学习的目标函数定义为

其中,Re(·)表示正则项,P可以看作重构矩阵.
2.2 DPLH算法的思想
在描述DPLH算法之前,先对本文用到的符号进行说明.为了描述方便,本文只考虑两种模态,例如:图像和文本,当然算法可以很容易扩展到多于两种模态的情况.用X(k)={x(1k),x(2k),···,x(Nk)}表示第k个模态的特征描述,k=1,2.X(k)∈Rdk×N,{x(i1),x(i2)}表示第i个样本由不同模态描述构成的样本对.其中,dk表示第k个模态的特征空间的维数,N表示样本对的数量.用Ak∈Rc×N表示第K个模态的系数矩阵,Dk∈Rdk×c表示第k个模态的字典,Pk∈Rc×dk表示第k个模态的哈希函数(即上面提到的重构矩阵),B(k)∈{0,1}c×N表示第k个模态的哈希码,其中c表示哈希码的长度.本文把两个模态纳入到一个学习框架中,则映射字典学习算法的目标函数定义为
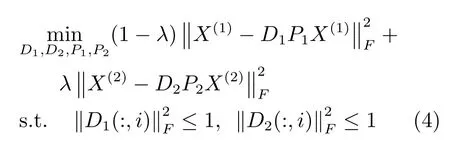
其中,前两项是重构误差,β,λ为权重参数,D1(:,i)表示字典D1的第i个字典原子,D2(:,i)表示字典D2的第i个字典原子.
跨媒体检索的目标是学习一个低维的共享子空间,异构数据之间的相似度可以在此空间直接度量.样本对虽然用不同模态表示,但它们包含相同的语义信息,因此在学习的子空间中,它们的差异应该尽量小.文献[13]把协同矩阵分解引入到子空间学习,但是样本对在学习的子空间中相同表示的强约束条件,可能会导致算法性能的下降.因此,本文放松了此约束,目标函数定义为
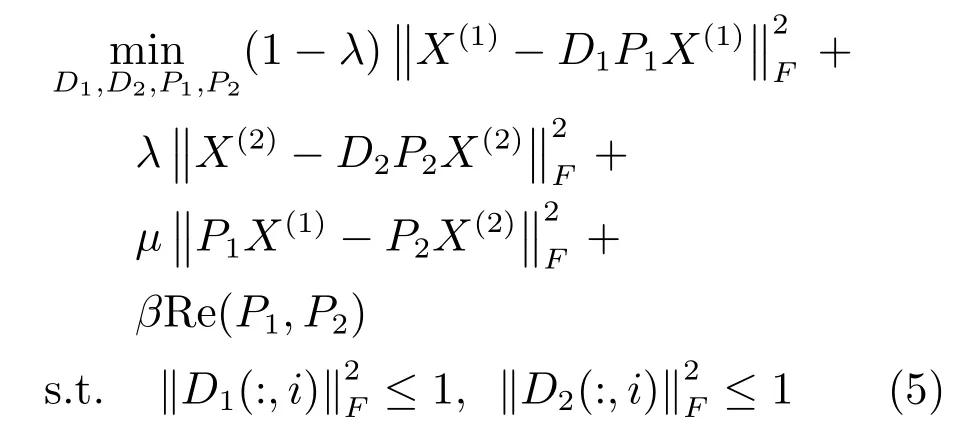
2.3 迭代优化算法
为了更容易求解式(4),为两个模态分别引入一个中间变量A1和A2,目标函数可写为
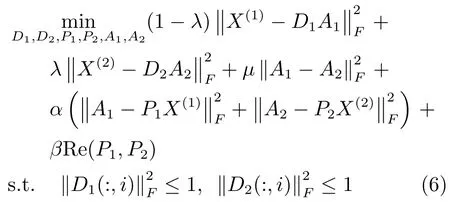
其中,参数α为权重.
式(6)的求解是一个非凸优化问题.幸运的是,当求解一个变量而固定其他变量时,问题就变为凸的,所以可以利用迭代的方法求解.
1)固定其他变量求解A1,则式(6)可写为

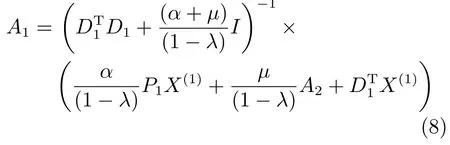
同理

2)固定其他变量求解P1,则式(5)可写为

展开上式并对P1求导,令其导数为零,可以得到闭合解.

同理

3)固定其他变量求解D1,则式(5)可写为

式(13)可以用文献[27]提出的ADMM 算法求解,同理D2也可以用相同方法求解.
上述过程不断迭代,直到目标函数收敛为止.
2.4 学习正交旋转矩阵
在得到哈希函数P1,P2后,测试样本的哈希码可以通过哈希函数直接得到.
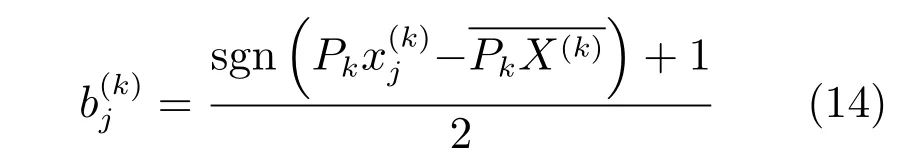
其中,sgn(·)表示符号函数,表示第k个模态映射到子空间的样本均值.在这里减去均值是为了保证哈希码0和1分布均匀.
式(14)表示对于Pk的任意一行Pk(i),如果满足,则,否则.然而式(14)的量化运算会带来量化损失,而损失的大小会直接影响算法的性能,通常量化损失越小越好.但是,大部分现存的哈希算法,直接利用式(14)得到哈希码,而没有考虑量化损失对哈希函数性能的影响[1−5,13−14,19].文献[6]提出了通过最小化量化误差学习一个旋转矩阵,以得到性能更好的哈希函数,提升了算法的性能.受此启发,本文得到哈希函数P1,P2后,通过最小化量化误差,学习一个正交变换矩阵,得到性能更好的哈希函数.量化产生的损失定义为

固定R,求B(i).

固定B(i),求R.

式(17)是典型的Orthogonal Procrustes problem,可以由奇异值分解(Singular value decomposition,SVD)的方法解决.为了最小化量化误差,哈希函数更新为RPi.
下面证明RPi不仅可以最小化量化误差,而且同时是目标函数(式(5))的局部最优解,即正交不变定理.
定理1.设R是c×c的可逆正交变换矩阵,满足RTR=Ic.如果P1,P2,D1,D2,A1,A2是式(6)的局部最优解,则RP1,RP2,D1RT,D2RT,RA1,RA2也是式(6)的优化解.
证明.
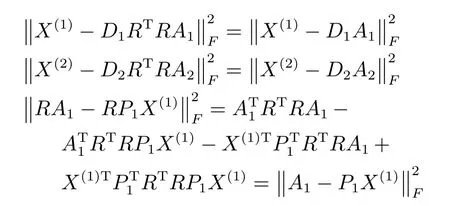
同理,

定理1证明了式(6)的局部最优解并不是唯一的,存在正交变换矩阵R,使RPi也是式(6)的一个局部最优解,因此直接优化式(6)得到的解并不一定是问题的最优解.本文通过最小化量化损失学习一个正交变换矩阵R,使得RPi既是式(6)的局部最优解,又满足量化损失最小,提升了算法的性能.
2.5 复杂度分析
在训练过程中,计算复杂度包括两部分:目标函数的求解和正交旋转矩阵的求解.
目标函数的求解过程是迭代优化的过程,不断迭代更新P1,P2,D1,D2,A1,A2,直到算法收敛,因此训练的计算复杂度主要产生在迭代更新过程.在这里,首先分析一下更新每个变量的计算复杂度.在更新变量Ai,i=1,2的表达式中,第1项计算复杂度为O(c2di+c3),第2项的计算复杂度为O(cdiN),因此更新Ai的计算复杂度为O(c2di+c3+cdiN+c2N).对于变量Pi,通过观察发现,Pi包含常数项(X(i)X(i)T+βI)−1,计算它们的时间复杂度为O(d2iN+d3i).但只需要在迭代前计算一次,并存储,在迭代过程中,只需读取即可,从而降低计算复杂度.因此迭代Pi的计算复杂度为O(cdiN+cd2i).利用ADMM 算法更新Di的计算复杂度为O(diN+c3+c2di+cd2i).
正交旋转矩阵的求解也是利用迭代算法.其中,更新R首先要计算B(i)VT的SVD分解,即B(i)VT=SΩˆST,而R=ˆSTS,所以总的计算复杂度为O(c2N+c3).而更新B(i)的时间复杂度为O(c2N).
在大数据时代,数据量非常大.通常在实际应用中N的值很大,一般情况下,N远远大于di和c的值.因此,整个迭代训练过程的计算复杂度为O(N),即与训练数据集的大小是线性关系.训练过程的计算复杂度低,保证了算法的可扩展性.
而对于测试过程,因为本文生成了哈希函数,测试样本的哈希码可以直接通过哈希函数得到,所以两个模态的计算复杂度分别为O(cd1)和O(cd2).而检索过程为求哈希码的距离,可以通过高效的异或运算实现.因此,测试过程的计算复杂度也很低.
3 实验结果
在实验中,本文主要通过两个检索任务验证算法的有效性:利用图像检索文本和利用文本检索图像.通过实验结果发现,本文提出的无监督算法,在某些情况下取得了优于监督算法的性能,证明了算法的有效性.
PDLH有4个参数,参数λ是一个平衡参数,控制两个模态的权重,在实验中发现这个参数鲁棒性较强,本文设置λ=0.5,表明两个模态的重要性相同.参数α控制重构系数矩阵产生的损失的权重,此参数也具有一定的鲁棒性,根据经验本文取α=0.3.参数µ是模态间相似性保持的权重,在跨模态检索中µ的作用较大,因此应该取较大的值,根据经验本文设置µ=2.参数β是正则化项的权重,因此应该取较小的值,根据经验本文设置β=0.02.
为了验证迭代优化算法的有效性,本文在Wiki和NUS-WIDE数据集上进行了实验(哈希码长为32bits),实验结果如图1所示.通过图1发现本文提出的优化算法收敛速度很快,在少于20次迭代后便收敛,说明了优化算法的有效性.
3.1 实验数据集
本文在Wiki[29]和NUS-WIDE[30]两个公开数据上进行实验,并与现存算法比较,以验证本文算法性能.

图1 算法的收敛性分析Fig.1 Convergence analysis of the proposed optimization algorithm
Wiki数据集:包含2866个文档,这些文档是从维基百科收集的,每个文档由一张图片和描述它的一段文本组成,这些文档可以分为10类.数据集中每张图片用128维的BOW特征向量表示,而每段文本用10维的Latent Dirichlet allocation(LDA)特征向量表示.其中,随机选择75%的文档构成训练集,剩余的25%构成测试集.
NUS-WIDE数据集:包含269648张图片,这些图片是从Flickr上收集的.每张图片与它对应的标注词构成图像–文本对,每张图片平均有6个标注词.这些样本对被分为81个类,然而有些类的样本数量很少,为了保证每类有足够多的训练样本,本文选取了样本数量最多的10个类,186577个样本对.其中图片用500维的BOW向量表示,而文本用1000维的BOW向量表示.参照文献[13,19]的设置,本文从数据集中随机选择99%的图像–文本对构成训练集,剩余的1%构成测试集.
3.2 对比算法及评价标准
为了验证PDLH算法的有效性,将PDLH与现有算法在两个公开数据集上的实验结果进行对比,现有算法包括CCA[6],CVH[12],CMFH[13],SCM[19],LSSH[14]和STMH[31].其中文献[19]使用了两种优化算法:正交优化算法和序列优化算法,本文分别用SCM-O和SCM-S表示.并且SCM算法利用标签建立相似矩阵,所以为监督的跨模态哈希算法,而其他方法为无监督算法.为了验证本文提出的利用映射字典学习子空间方法的有效性,本文利用PDLH-表示去除旋转矩阵的实验结果.
在实验中,因为STMH算法的代码没有公开,所以由我们实现,而其余对比算法的代码都由作者提供.所有代码的参数都经过调试,并且我们报告的是最好的实验结果.在实验中,本文以标签作为判定标准,即两个样本的标签至少含有一个相同的类,才判定这两个样本为同一类.
在实验中,本文利用广泛应用于哈希算法的Mean average precision(MAP)来评估各算法的性能.Average precision(AP)的定义如下:

其中,r为检索到的样本数量,L为检索到的正确样本的数量,prec(i)为前i个样本的准确率,δ(i)为指示函数,当第i个样本为正确样本时δ(i)=1,否则δ(i)=0.而MAP为所有测试样本AP的平均.
本文用每个测试样本检索返回的前200个样本计算MAP,记为MAP@200.为了进一步证明PDLH的有效性,本文绘制了Precision-recall(PR)曲线图,PR曲线反映了不同正确样本召回率对应的准确率.
3.3 Wiki数据集的实验结果
由于Wiki数据集较小,所以本文利用所有训练集的样本训练哈希函数.在实验中,本文测试了不同哈希码长的算法性能,其中MAP的实验结果见表1.从表1可以看出,1)PDLH,CMFH和SCM-S算法的性能较好,PDLH在大多数码长取得了最好的实验结果,只在少数码长低于SCM-S或CMFH的性能;2)在所有码长情况下,PDLH的结果都优于PDLH-的结果.这证明了正交旋转矩阵通过最小化量化误差提升了算法的性能;3)即使在去除旋转矩阵的情况下,本文提出的算法也取得了良好的性能.这说明利用映射字典学习不仅降低了算法的时间复杂度,而且通过字典学习,使哈希码含有语义信息,增强了哈希码的区分能力,因此得到了令人满意的实验结果.
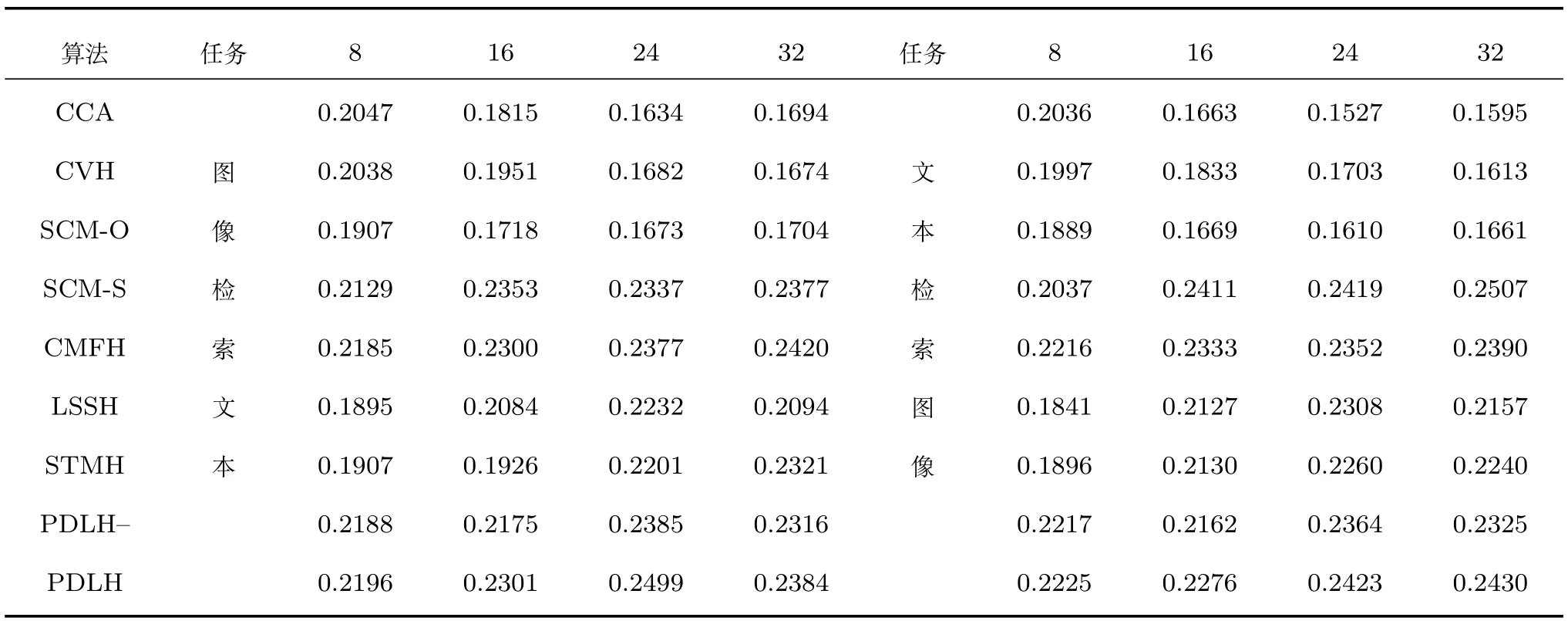
表1 图像检索文本和文本检索图像任务在Wiki数据集上的实验结果(MAP@200)Table 1 MAP@200 results on Wiki dataset for the tasks of using the image to query texts and vice versa
SCM-S是监督哈希算法,在哈希函数学习过程中不仅利用了特征信息,而且利用了所有样本的标签信息来获得更好的哈希函数.然而,获得所有样本的标签,要耗费大量的人力物力,在大数据时代,是不可能实现的,所以本文算法更具有应用价值.
为了进一步证明本文提出算法的有效性,图2和图3分别绘制了码长为16bits和32bits时各个算法在两个任务上的的PR曲线图.从图2和图3可以看出,PDLH和SCM-S算法取得了较好的性能,而PDLH在召回率较低时性能更好一些.这在实际应用中非常重要,因为用户在检索时,往往更关注排列在前的返回样本.
3.4 NUS-WIDE数据集的实验结果
由于NUS-WIDE的训练集较大,而LSSH和SCM-O需要大量的训练时间.为了降低时间复杂度,参照文献[13]的参数设置,本文从训练集中随机选出5000个样本对构成训练集,而测试集包含的1%的样本对全部用作测试.MAP的实验结果见表2.从表2可以看出,在图像检索文本任务中,PDLH在各码长都得到了最好的结果,而且性能明显优于其他算法.而在文本检索图像任务中PDLH和监督算法SCM-S取得了明显优于其他算法的结果.而且即使在去掉旋转矩阵的情况下,本文算法依然在大多数情况下取得了最好结果.实验结果再次证明了算法既降低了复杂度,又提升了子空间的区分能力.同时也验证了使哈希码含有语义信息提升了算法的性能(在大部分情况下,性能超过监督算法SCM-S,其余情况下,性能逼近监督算法SCM-S).
为了进一步证明本文提出算法的有效性,图4和图5分别绘制了码长为16bits和32bits时各个算法在两个任务上的的PR曲线图.从图4和图5可以看出,与MAP的结果类似,PDLH算法和监督算法SCM-S的性能在NUS-WIDE上明显优于现有其他的无监督算法.而与监督算法SCM-S相比,PDLH在召回率较低时性能较好,这与在Wiki数据集上的结果类似.
为了进一步验证本文算法的可扩展性,本文设定哈希码码长为16bits,并对训练集的大小进行了不同设定,训练时间和MAP的实验结果见表3所示.从表3可以看出,随着训练集样本数量的增加,算法的性能不断提升.这是很合理的,因为随着训练集样本数量的增多,训练样本包含样本间的内在联系信息越丰富,因此可以学习更好的哈希函数.而且通过表3还发现训练时间与样本的尺寸基本呈线性关系,从实验上验证了本文之前的复杂度分析.
4 结论
针对哈希码语义无关而导致性能下降的问题,本文提出了一种基于映射字典学习的跨模态哈希检索算法.算法利用映射字典学习降低了算法复杂度,并生成了哈希函数,这与现存字典学习哈希方法不同.最后在两个公开数据集上的实验结果证明了算法的有效性.将来的工作主要包括学习一个更好的子空间表示,减小量化误差对哈希函数的影响和利用非线性变换更好地捕捉样本间的内在联系.

图2 码长16bits在Wiki数据集的PR曲线图Fig.2 PR curves on Wiki dataset with the code length fixed to 16bits
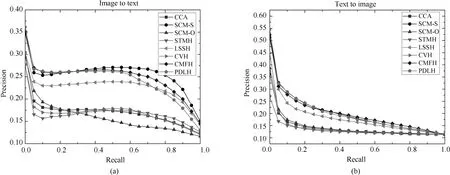
图3 码长32bits在Wiki数据集的PR曲线图Fig.3 PR curves on Wiki dataset with the code length fixed to 32bits

表2 图像检索文本和文本检索图像任务在NUS-WIDE数据集上的实验结果(MAP@200)Table 2 MAP results on NUS-WIDE dataset for the tasks of using the image to query texts and vice versa(MAP@200)
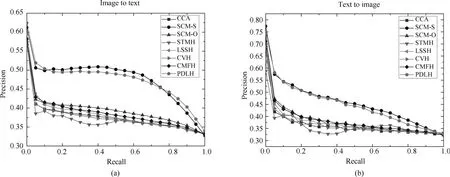
图4 码长16bits在NUS-WIDE数据集的PR曲线图Fig.4 PR curves on NUS-WIDE dataset with the code length fixed to 16bits

图5 码长32bits在NUS-WIDE数据集的PR曲线图Fig.5 PR curves on NUS-WIDE dataset with the code length fixed to 32bits

表3 不同数量训练样本的训练时间(s)和MAP结果Table 3 The time costs(s)and MAP results with different sizes of training dataset
