基于混合地理加权回归与克里格的区域降水量空间插值方法*

李 豪，刘 涛，徐精文



基于混合地理加权回归与克里格的区域降水量空间插值方法*

李 豪，刘 涛，徐精文

（四川农业大学资源学院，成都 611130）

基于四川省区域范围内144个气象站点的实测降水数据，在综合考虑空间位置、地形等影响因素的基础上，采用改进的回归克里格模型，即混合地理加权回归克里格模型（MGWRK）对四川省年降水量的空间分布进行空间插值，并与普通克里格（OK）、全局回归克里格（GRK）和地理加权回归克里格（GWRK）等模型的插值效果进行对比分析。结果表明：（1）应用逐步回归法筛选确定的用于回归分析的影响因子组合为经度、纬度和坡度，可有效消除解释变量间的多重共线性，为后续的空间插值奠定基础；（2）同一回归变量在地理加权回归（GWR）与全局回归（GR）两种回归模型中的AICc（修正的赤池信息量准则，Corrected Akaike Information Criterion）值之差（ΔAICc）可用于定量判定各回归变量的空间非平稳性类型，据此将变量坡度设为全局变量，经度和纬度设为局部变量进行处理。在此基础上，通过MGWRK模型对四川省年降水量进行空间插值；（3）MGWRK插值模型综合考虑了空间位置、地形等多个影响因素及其与降水相互关系的空间非平稳性特征，相对于传统的OK和GRK法具有更高的插值精度。

降水量；混合地理加权回归；克里格；空间插值

降水是气象、农业和环境等领域研究的重要数据源，对农业生产、区域水资源管理、防洪减灾、生态环境治理等工作均具有重要的应用价值。近年来，随着众多领域研究工作的深入，对区域降水数据在空间尺度上的精细化需求也逐步提升。

在空间尺度上，目前获取区域降水数据的方法主要有两种：一是气象站的观测[1]，这是现阶段最主要、技术最成熟的手段，具有测量精度高、稳定可靠等优点。但该方法获得的数据为离散的点数据，无法提供区域内任意位置的降水资料，且由于受到地形条件及资金投入等的限制，现阶段仍存在站点间距离较大、密度偏低等不足，由此获取的降水数据往往难以满足小尺度研究对数据精细度的需求。另一种方法是卫星遥感降水数据。该方法不直接测量降水，而是通过卫星上搭载的传感器测定云顶红外温度、雷达反射率等数据，再反演获取降水数据[2]，TRMM、GSMaP和GPCP等降水数据集均属此类。该方法获得的降水数据为连续的面数据，但大多着眼于全球尺度，空间分辨率相对较低，如TRMM数据的分辨率仅为0.25°×0.25°，一些局部、细节性的降水空间分布特征未能表达出来，且存在不同区域反演精度差异大、覆盖范围有限等不足[2]，亦无法完全达到区域、流域或更小尺度研究对降水数据的精度要求。

以实测数据为基础、基于GIS的空间插值技术已广泛用于获取气象、土壤和环境等要素的高分辨率空间分布数据。该方法是气象站观测法的延伸，通过离散的气象站实测数据预测未知区域的降水数据，可以快速获取全面、高空间分辨率的区域降水资料，有效解决上述两种方法的不足，是目前获取区域降水空间数据的重要途径，特别在具有充足地面观测资料的地区具有较好的适用性和较高的估算精度[3−5]。

目前，用于降水数据的空间插值方法很多，不同方法的预测精度也不尽相同。根据已有数据与研究区域的空间分布特征，选择一种最优的插值方法是采用该方法获取区域降水数据的关键。克里格（Kriging）法是基于地统计学的一种空间插值方法，它充分考虑了样点的空间变异性特征，具有适用性强、预测精度高等优点，目前在气象、生态和土壤等领域的应用最为广泛[6−8]。已有研究表明，通过构建回归克里格（Regression Kriging，RK）模型，将克里格插值与回归分析结合起来，引入与插值变量具有较好相关性的影响因子作为辅助变量，建立插值变量与其影响因子之间的回归模型，可以有效提高克里格法的插值精度[9−12]。

本研究以地处长江上游、降水空间分异显著的四川省为研究对象，在充分考虑降水量与各影响因子间相互关系及其空间非平稳性特征的基础上，尝试采用一种改进的回归克里格插值模型，即混合地理加权回归克里格模型（Mixed Geographically Weighted Regression Kriging，MGWRK）对四川省年降水量的空间分布进行预测，并与全局回归克里格、普通地理加权回归克里格等方法的插值结果进行对比分析，探寻适合本区域降水量的空间插值方法，从而准确获得四川省年降水量空间分布的精细化数据，以期为在该区域开展农业产业结构优化、水资源配置、生态环境治理等工作提供有效数据支持。

1 资料与方法

1.1 研究区概况

四川省位于中国西南，地处长江上游，介于92°21′−108°12′E、26°03′−34°19′N，区域面积48.5万km2[13]。本区位于第一级青藏高原和第二级长江中下游平原的过渡带，海拔高差悬殊，地貌复杂多样，以山地地貌为主，西高东低，全省可分为东部四川盆地、川西北高原和川西南山地等三大部分。

区内季风气候明显，气候类型多样，差异显著。东部四川盆地为亚热带湿润、半湿润气候，雨热同季，水热条件好，年均温16～18℃，年降水量达1000～1200mm，50%以上集中在夏季；西北部为高山高原高寒气候，气候垂直变化明显，总体上以寒温带气候为主，冬寒夏凉，水热不足，年均气温4～12℃，年降水量500～900mm；

1.2 数据来源

四川省144个气象站点的年降水量（观测精度为0.1mm）、经纬度等数据来自中国气象局国家气象信息中心提供的“中国基本、基准和一般地面气象观测站1981−2010年累年值年值数据集”。各气象站点的空间分布如图1所示。该数据集均为地面实测数据，可信度高，且站点数量多，能够保证空间插值的精度，满足研究要求。

研究区域的地形数据（Digital Elevation Model，DEM）来源于目前应用最为广泛的美国太空总署（NASA）空间科学数据中心提供的SRTM数据，空间分辨率为90m，研究前对DEM数据进行了填洼处理，移除其中的小缺陷，并采用Bilinear法重采样至1km。其它衍生地形数据（坡度、坡向等）通过1km分辨率的DEM数据在ArcGIS软件中利用空间分析工具箱的Slope和Aspect工具提取得到。其中坡向指地表一点的切平面的法线矢量n在水平面的投影nxoy与过该点的正北方向的夹角。

图1 四川省144个气象站点分布图

1.3 研究方法

区域降水的空间分布受诸多因素的影响，而本研究区地处内陆山区，地形特征是影响其降水量空间分布的主要因素[14−15]。因此，选择表达空间位置的经度、纬度，以及表达地形的海拔、坡度和坡向共5个影响因子作为辅助变量，用于回归分析和空间插值。

1.3.1 普通克里格插值法（OK）

克里格插值法是一种基于地统计学的经典空间插值方法，目前已在多个领域得到广泛应用。但对于部分受多种因素影响、具有高度空间异质性的目标变量而言，传统的普通克里格法（Ordinary Kriging，OK）的插值精度往往受到较大的限制[16]。

1.3.2 回归克里格插值法（RK）

回归克里格（RK）法[17]是将克里格插值法与回归分析结合起来的一种空间插值方法，已有研究表明，与OK法相比，RK法通常能够取得更高的预测精度[18−20]。RK法的基本思想是采用不同方法对目标变量的主要影响因素和随机因素（即回归残差）分别进行分析，首先建立目标变量和影响因素之间的回归方程，分离出趋势项，然后对回归残差采用OK法进行插值，最后对回归分析得到的趋势项和OK法得到的残差的估计值进行求和，最终得到目标变量的预测值。RK法可表达为[12]

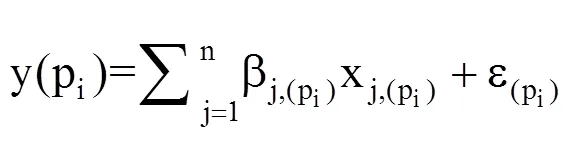
式中，y(pi)为位置pi处的目标变量，βj,(pi)为回归系数，xj,(pi)为位置pi处的第j个自变量，ε(pi)为位置pi处的回归残差，n为自变量的个数。

（1）全局回归（GR）方法。在RK法的应用中，回归分析部分大多采用基于最小二乘法（Ordinary Least Square，OLS）的全局回归（Global Regression，GR），即全局回归克里格法（GRK）。由于其仅对解释变量进行“均值”估计，各回归系数为常数，不能反映变量的空间非平稳性，因此，在处理土壤、降水等这类空间非平稳性较强的变量时，GRK法插值精度的提高仍受到限制。

（2）地理加权回归（GWR）方法。针对上述问题，Fortheringham等基于局部光滑思想，提出了地理加权回归（Geographically Weighted Regression，GWR）模型用以处理回归分析中解释变量的空间非平稳性[21−22]。GWR模型是对普通GR模型的扩展，其采用了局部回归（Local Regression，LR）方法，对空间非平稳性进行量化。在GWR中，解释变量的回归系数不再是常数，而是空间位置的函数（称之为空间权重函数），式（1）中位置(ui,vi)处的回归系数β通过下式计算得到[22]

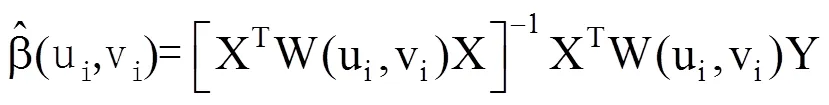
式中，β为回归系数矩阵；X为解释变量设计矩阵，XT为其转置矩阵；Y为因变量矩阵；W(ui,vi)为空间权重矩阵，由空间权重函数W(i)求得，其作用是定量衡量领域内不同空间位置j（j=1，2，…，n）样点的观测值对于回归点(ui, vi)回归系数估计的影响程度。GWR模型能有效捕捉空间非平稳性特征，更加真实地反映出目标变量的空间变异情况。而基于GWR构建的地理加权回归克里格（Geographically Weighted Regression Kriging，GWRK）法能使空间插值的预测精度得到进一步提高[11−12]。

（3）混合地理加权方法（MGWR）。在许多实际问题中，解释变量中往往同时包含了全局变量和局部变量：一些解释变量具有明显的空间非平稳性，适合使用GWR法建模；而另一部分解释变量可能不具有空间非平稳性，或其空间非平稳性非常小可忽略不计，宜用多元GR法建模。为此，Brunsdon等在GWR模型基础上，提出了混合地理加权模型（Mixed Geographical Weighted Regression，MGWR）[23]。在MGWR模型中，同时包含了回归系数恒定的全局变量和随地理位置变化而变化的局部变量，MGWR模型的基本形式为

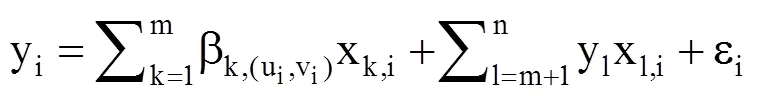
式中，yi、βk,(ui,vi)和εi的含义同式（2），xk,i为位置i处的第k个局部变量，xl,i为位置i处的第l个全局变量，γl为全局回归的回归系数（常数），m为局部变量的个数，n为解释变量的个数。

运用MGWR模型的关键在于通过判定各解释变量在进行回归分析时的空间非平稳性类型，即某个解释变量属于全局变量还是局部变量。但现有研究大多通过主观经验、定性判断来确定，基于定量方法分析该问题的报道还较少见。

MGWR模型可解决多个解释变量不同空间平稳特性共存的问题，较之单一的GR模型与GWR模型，能更准确地反映变量间的空间变化关系，有效提高模型的解释能力｡降水的影响因素中可能同时包含空间平稳和空间非平稳两种类型，MGWR法适用研究降水与其影响因素间的相互关系。

本研究在深入分析各影响因素的空间平稳性特征的基础上，采用混合地理加权回归克里格法，即将回归克里格法中回归分析部分替换为MGWR模型，其余步骤、方法保持不变，对四川省年降水数据进行空间插值，并探讨具有高预测精度、合适本区域复杂地形条件的降水数据空间插值方法。

1.4 模型精度的评价

采用五折交叉验证法（Five-fold cross validation）对各模型的插值精度进行评价。将144个气象站点随机分为5等份（每份29个站点），每次拿出其中一个（站点总数的20%）作为验证集，验证数据不参与回归分析和克里格插值过程，只用于模型精度的评价。将其余4份数据（站点总数的80%）作为建模集进行空间插值，该过程共进行5次，并求取各验证数据集站点的年降水量模拟值。通过计算平均误差（Mean Error，ME）、平均绝对误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Square Error，RMSE）[12]、平均绝对百分误差（Mean Absolute Relative Error，MARE）和均方根相对误差（Root Mean Square Relative Error，RMSRE）等指标的5次平均值评价不同插值模型的预测精度。其中，MARE和RMSRE定义为

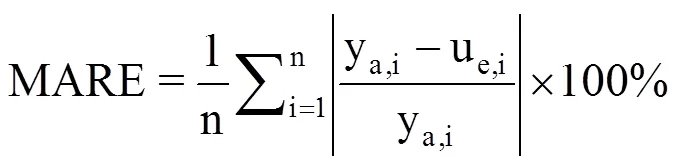
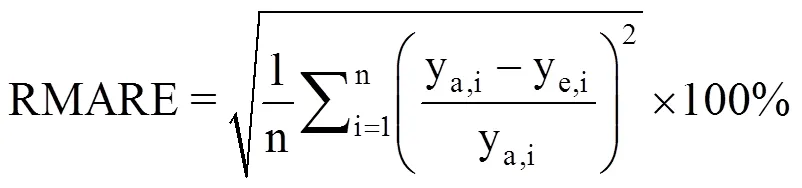
式中，ya,i为位置i处的年降水量实测值，ye,i为位置i处的年降水量模拟值，n为验证数据集的站点个数。

1.5 分析步骤

（1）对各气象站点的降水数据进行预处理，包括描述性统计分析、正态性检验等。

（2）分析研究区域站点的年降水量（目标变量）与各影响因子变量间的相关性，采用逐步回归分析方法，筛选出用于后续回归分析的影响因子变量。

（3）采用GR、GWR和MGWR三种方法，以站点年降水量为因变量，上一步筛选的影响因子为解释变量进行回归分析。

（4）用OK法对上述各回归分析的残差进行空间插值，并将残差插值结果与回归分析得到的趋势项相加，得到四川省年降水量的空间分布图。

（5）通过验证数据集评价不同插值模型的预测精度。

1.6 软件平台

描述性统计分析采用SPSS 23完成，基于OLS的GR、GWR和MGWR等回归分析通过GWR4完成，半方差函数计算通过地统计学软件GS+9进行，OK法插值和降水量空间分布图的绘制由ArcGIS 10.4完成。各变量空间分布图的分辨率均为1km。

2 结果与分析

2.1 建模前准备

2.1.1 建模用降水数据序列的正态性检验

对建模用气象站点的年降水量数据进行描述性统计分析和正态性检验，表1表明，研究区域各站点的年降水量介于346.9～1670.0mm，平均968.1mm；变异系数达到23.06%，变异程度中等。站点的年降水量数据序列通过了J−B（Jarque-Bera）检验（P＜0.05），符合正态分布。

表1 研究区站点的年降水量描述性统计分析和正态性检验（1981−2010年）

2.1.2 模型影响因子变量筛选

年降水量与各影响因子的Pearson相关系数见表2。由表可知，除坡向外，年降水量与其余各影响因子间均存在较高的相关性，具体表现为与经度和海拔呈显著正相关，与坡度呈极显著负相关，与纬度呈显著正相关。另一方面，各影响因子间也存在一定程度的相互作用，如海拔与经度呈极显著负相关，相关系数达到−0.788，可见，部分影响因子间存在较强多重共线性（Multicollinearity），将对插值模型的构建产生不利影响。

表2 年降水量与各影响因子的相关系数（115个建模站点）

注：*、**分别表示相关系数通过0.05、0.01水平的显著性检验。下同。

Note:*is P<0.05,**is P<0.01. The same as below.

表3 年降水量与各影响因子的逐步回归过程（n=115）

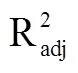
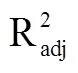
表4 表3中模型5的回归计算结果（n=115）

2.2 地理加权回归模型的构建

以上一步筛选的经度、纬度和坡度3个影响因子为局部变量进行地理加权回归，结果见表5。由表中可见，各解释变量的回归系数处于一定的变化范围，不再是常数，如经度的回归系数的取值范围介于−118.89～265.63，变异系数达到283.21%，说明降水量与各解释变量间的相互关系具有显著的空间非平稳性。

通过ΔAICc判定各解释变量的空间非平稳性类型。AICc是用于检验回归模型及模型中变量拟合优度的常用指标之一，其值越小，拟合效果越佳[25]。本研究中ΔAICc是指同一变量在GWR和GR两种回归模型的AICc值之差，其值为正，即GWR模型的AICc值大于GR模型的AICc值，说明将该变量视为局部变量、采用GWR模型进行回归的效果不如GR模型。Nakaya等认为，若ΔAICc值大于2，可以认为该变量不存在明显的空间非平稳性，进行回归分析时应将其从局部变量调整为全局变量[26]。从3个解释变量的ΔAICc值来看，经度和纬度的ΔAICc值均为负数，说明在进行回归分析时将这些变量作局部变量处理是合理的；而坡度的ΔAICc值达11.359，远大于2，说明其空间非平稳性不明显，应将该变量作为全局变量处理。因此，以站点的经度和纬度为局部变量，坡度为全局变量，采用MGWR法再次进行回归分析。由表6的MGWR分析结果可见，将坡度设为全局变量后，其回归系数也随之变为常数（−3.425），说明总体上坡度与年降水量之间为负相关关系。

表5 地理加权回归模型（GWR）回归计算结果（n=115）

注：ΔAICc是同一变量在GWR和GR两种回归模型的AICc值之差。

Note: ΔAICc is the difference between the value of AICc of the same variable calculated by GWR model and that by GR model.

表6 混合地理加权模型（MGWR）回归计算结果（n=115）

表7 三种回归模型的诊断指标

2.3 回归模型残差的克里格插值

正态性检验结果显示，GR、GWR和MGWR三种模型的残差不符合正态分布。因此，对残差数据进行3/5次方转换，经转换后使其满足进行克里格插值的条件。在GS+9软件中，对3种经3/5次方转换后的回归残差进行半方差函数分析。从表8可看出，各半方差函数的决定系数R2均达到0.60以上，取得了较好的拟合效果；各半方差函数的块基比［即C0/ （C0+ C）］均小于20%，说明各回归残差存在较强的空间自相关性，适合使用克里格法进行空间插值。

表8 各回归残差的半方差函数拟合结果

根据半方差函数的分析结果，采用OK法分别对各模型的残差进行空间插值，得到回归残差的空间分布图（回归残差进行3/5次方转换后进行插值，得到插值结果后再进行逆转换）。通过各影响因子变量及其回归系数的空间分布图、残差插值结果图等分别获得基于GRK、GWRK和MGWRK模型的四川省年降水量的空间分布图。同时采用OK法直接对各站点的年降水数据进行空间插值。各模型的插值结果如图2所示。

由图2可见，各插值模型得到的四川省年降水量空间分布的总趋势基本一致，均呈现东高西低、盆地高高原低、盆周山地高盆中丘陵低的趋势，该预测结果与前人的研究基本一致[27]。此外，一些降水空间分布的细节在插值结果中也有所反映。如全省年降水的峰值区大致位于四川盆地西部边缘的山前丘陵、中山区，包括雅安的名山、宝兴和乐山的峨眉山等地。该区域呈长轴方向，为西北—东南向的椭圆形，区内各地的年降水量达到1300～1500mm。形成这一现象的主要原因是该区域西部、西北部和南部均有一系列高山阻隔，形成了特殊的“喇叭”状的地形，使东来的太平洋东南暖湿气流与盆周山地下沉的冷湿气流交汇于此，形成了著名的“华西雨屏”现象，使该区成为全省乃至中国内陆降水量最大的地区。

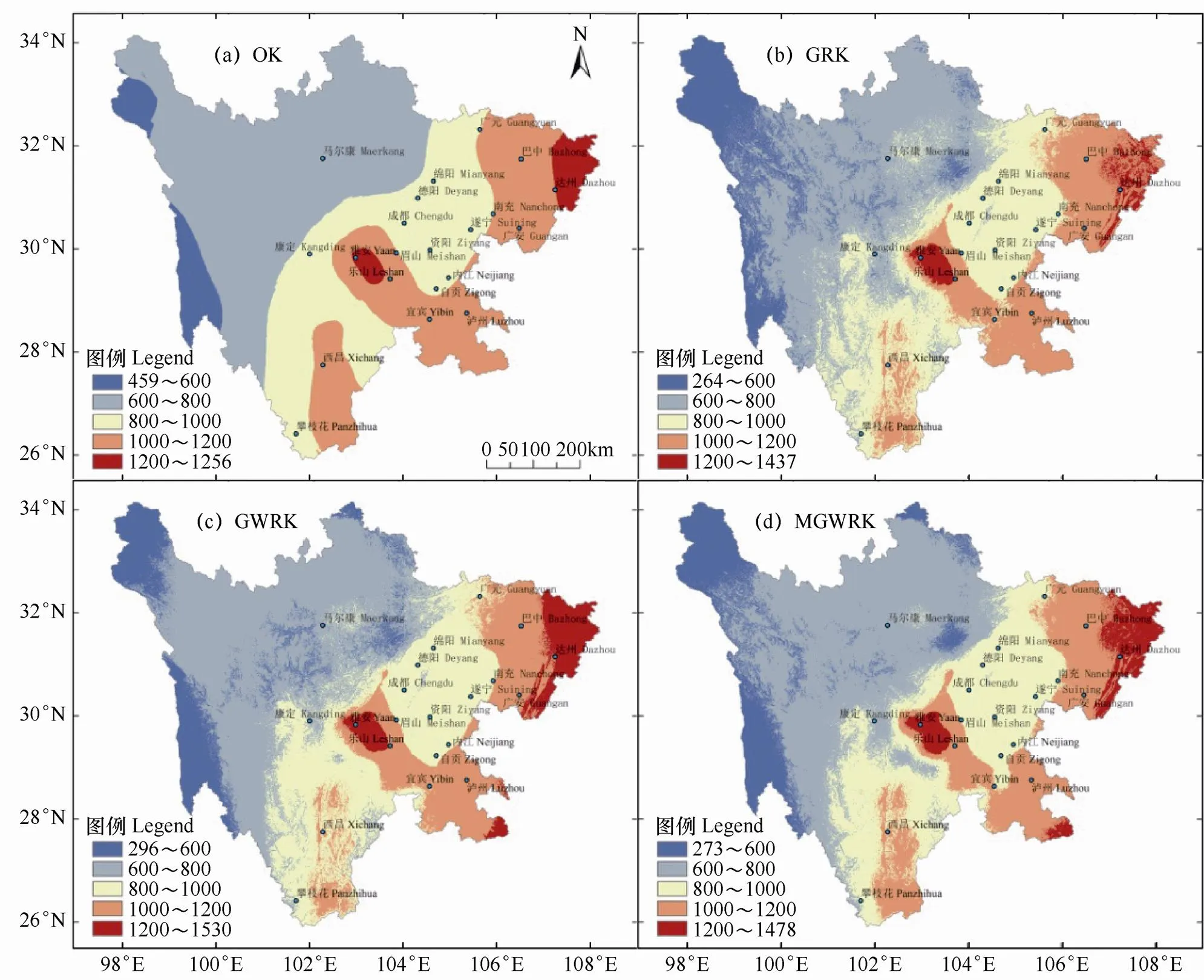
图2 基于不同模型的四川省年平均降水量空间分布（1981−2010年）

2.4 地理回归克里格插值模型的精度评价

采用五折交叉验证法，通过ME、MAE和MARE等指标评价各插值模型的预测精度。各评价指标的值越接近0，说明模型的插值精度越高。表9表明，各模型的插值精度大致表现为MGWRK＞GWRK ≈GRK＞OK。综合分析表明，包含空间位置、地形等多个影响因素的3种回归克里格模型对年降水量的插值精度较OK模型均有较大提高，如RMSRE值从OK的1.351显著减至MGWRK的0.897；GWRK模型虽然考虑了影响因子空间非平稳性，在回归效果上也优于GRK模型，但最终的插值精度与后者相比并没有明显的提高；而在4种模型中，进一步探究了各影响因子的空间非平稳性类型的MGWRK模型的插值精度最优。

根据144个站点的空间分布特征，通过Thiessen多边形法对研究区进行剖分，得到MGWRK模型插值残差（即实测年降水数据与MGWRK模型模拟值之差）的空间分布（图3）。从图3可看出，MGWRK模型的残差值介于−240～258，且分布较为集中，残差值介于−50～50的站点共有112个，占站点总数的77.78%，占全省总面积的81.91%。由此可见，采用MGWRK模型获得的年降水量数据在四川省大多数地区可取得较好的计算精度，插值残差总体而言处于一个较低水平。而残差高值区主要分布在研究区中西部的四川盆地西部边缘的山前丘陵、中山区，即上述的“华西雨屏区”，包括天全、泸定和峨眉山等站点。

表9 不同模型的插值精度分析

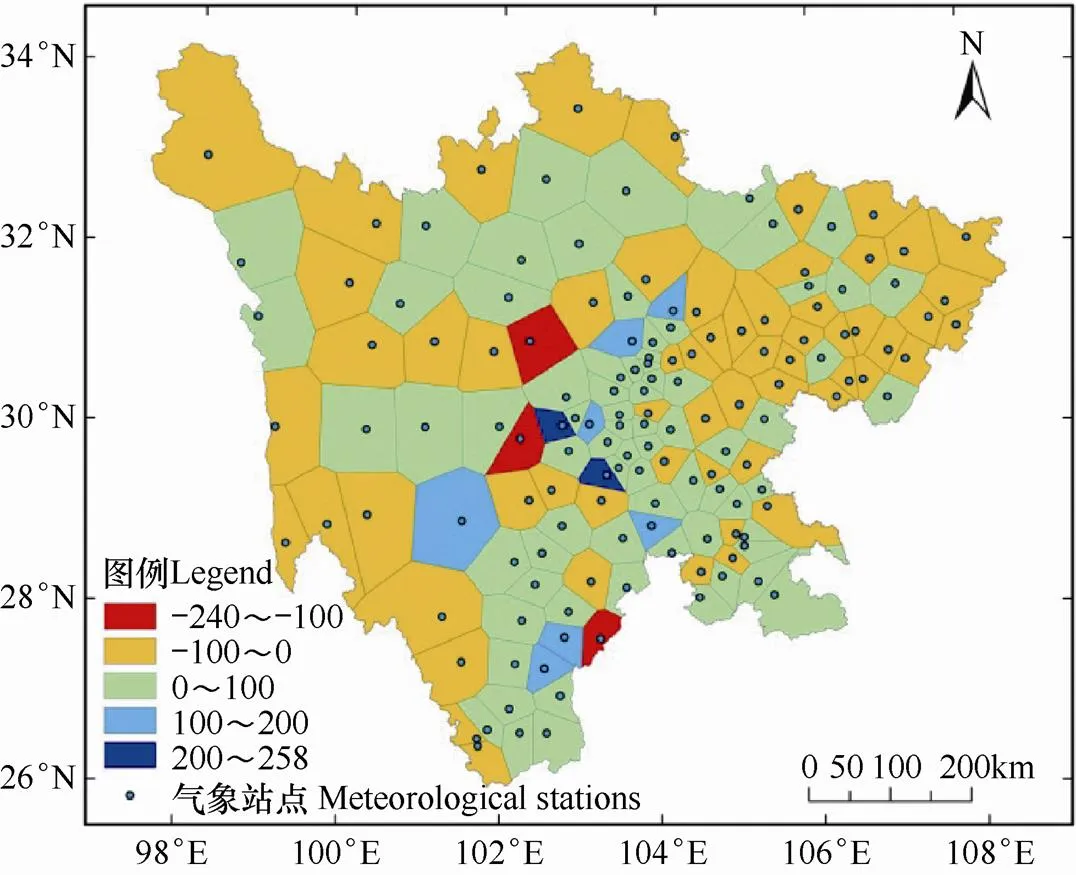
图3 MGWRK模型插值残差的空间分布

3 结论与讨论

3.1 讨论

区域降水的空间分布受到多方面因素的影响。前人研究表明，空间位置、大气环流以及地形因素均会对区域降水有一定的制约作用[14−15]。本研究在进行分析时充分考虑区域降水形成的物理过程，将空间位置和地形等主要影响因子纳入插值过程。研究结果表明，四川省年降水的整体空间分布主要受空间位置因素（即经度和纬度）的影响，GR模型的计算结果也证明了这一点：经度（55.804）和纬度（−47.083）的回归系数均远大于代表地形因子的坡度的回归系数（−7.915），说明整体上看，空间位置是影响四川省降水空间分布的主控因素，在较大空间尺度下，其对降水的影响占据主要地位，并导致地形对降水分布的影响相对不明显。另一方面，地形因素对降水的影响主要表现在局部地区，并往往会出现异常的地形降水分布。如四川盆地西部边缘的山前丘陵、中山区特殊的“喇叭”状地形，导致东来的太平洋东南暖湿气流与盆周山地下沉的冷湿气流交汇于此，形成了著名的“华西雨屏”现象，使得该区的年降水量要明显高于周围地区。

综合各种评价误差的计算结果可以看出，由于深入考虑了各影响因子与降水量相互关系的空间非平稳性，MGWRK法对提高降水空间插值的精度作用是明显的，其插值效果优于OK法等传统插值方法，能较准确地反映四川省降水分布实际状况，尤其是一些降水分布的细节性特征能较好地表达出来；在气象站点相对较少的四川省西部地区，其插值精度也能得到较好的保证。另一方面，不同地区的插值精度也存在一定差异。MGWRK法在降水分布符合主控因素（即空间位置）的地区具有较好的插值精度；而当降水分布出现异常，即地形因素对降水分布的作用增强时，如在上述年降水量远高于周围地区的华西雨屏带，插值效果则有所下降，误差相对较大，这与邬伦等学者的研究结论也是一致的[28−29]。

从时间尺度来看，本研究结果表明，就四川省多年平均气候状态下的降水而言，其空间分布的变化规律较明显，影响因素较少且明确，因此取得了较好的插值结果。但在实际应用时，对于较小时间尺度如日降水、逐小时降水等，影响降水空间分布的因素往往会增多，且随机性因素的作用也可能增强，MGWRK模型是否仍然适用，此外，对于制约降水分布的影响因素，本研究仅考虑了海拔、坡度、坡向等地形因子，尚未考虑大气环流等其它因子对降水的影响，加入这些影响因素是否有助于插值精度的进一步提高，这些问题都有待进一步深入研究，对插值模型进行改进。

3.2 结论

（1）用于回归分析的影响因子为经度、纬度和坡度，在MGWR回归分析中，坡度变量不存在明显的空间非平稳性，作为全局变量处理，而经度和纬度作为局部变量处理。

（2）综合考虑了空间位置、地形等多个影响因素的3种回归克里格模型（GRK、GWRK和MGWRK）的插值精度均优于OK模型，而进一步考虑了各影响因子与降水量相互关系的空间非平稳性，并深入探究了空间非平稳性类型的MGWRK模型的插值效果最佳。

（3）MGWRK插值模型以气象站点实测数据为基础，在考虑解释变量空间平稳性特征的基础上，进一步定量区分了解释变量的空间平稳性类型，由此获得的降水空间数据具有较高的插值精度，并能较准确地表达局部区域降水发生突变的细节信息。在空间插值研究中，辅助信息的加入有助于一定程度上提高预测精度。在此基础上，进一步厘清不同辅助信息在插值过程中所扮演的“角色”，如不同辅助变量的空间平稳性类型，可使插值精度得到进一步提高。

[1] 葛朝霞,曹丽青.气象学与气候学教程[M].北京:中国水利水电出版社,2009:213-215.Ge Z X,Cao L Q.A course on meteorology and climatology[M].Beijing:China Water and Power Press,2009:213-215.(in Chinese)

[2] 刘元波,傅巧妮,宋平,等.卫星遥感反演降水研究综述[J].地球科学进展,2011,26(11):1162-1172.Liu Y B,Fu Q N,Song P,et al.Satellite retrieval of precipita- tion:an overview[J].Advances in Earth Sciences,2011, 26(11):1162-1172.(in Chinese)

[3] 王智,吴友均,梁凤超,等.新疆地区年降水量的空间插值方法研究[J].中国农业气象,2011,32(3):331-337.Wang Z,Wu Y J,Liang F C,et al.Study on spatial interpolation method of annual precipitation in Xinjiang[J].Chinese Journal of Agrometeorology,2011,32(3):331-337.(in Chinese)

[4] 赵煜飞,朱江.近50年中国降水格点日值数据集精度及评估[J].高原气象,2015,34(1):50-58.Zhao Y F,Zhu J.Assessing quality of grid daily precipitation datasets in China in recent 50 years[J].Plateau Meteoro- logy,2015,34(1):50-58.(in Chinese)

[5] 李月,齐实,程伯涵,等.哀牢山山区降水时空分布的影响因素及插值方法比较[J].地球与环境,2017,45(6):600-611.Li Y,Qi S,Cheng B H,et al.A study on factors of space-time distributions of precipitation in Ailao Mountain area and comparison of interpolation methods[J].Earth and Environ- ment,2017,45(6):600-611.(in Chinese)

[6] 王红霞,柳小妮,李纯斌,等.甘肃省近42年降水量变化时空分布格局分析[J].中国农业气象,2013,34(4):384-389.Wang H X,Liu X N,Li C B,et al.Spatial temporal distribution of precipitation in Gansu Province last 42 years[J].Chinese Journal of Agrometeorology,2013,34(4):384-389.(in Chinese)

[7] 龙军,张黎明,沈金泉,等.复杂地貌类型区耕地土壤有机质空间插值方法研究[J].土壤学报,2014,51(6):81-93.Long J,Zhang L M,Shen J Q,et al.Spatial interpolation of soil organic matter in farmlands in areas complex in landform[J].Acta Pedologica Sinica,2014,51(6):81-93.(in Chinese)

[8] 赵晨曦,王云琦,王玉杰,等.北京地区冬春PM2.5和PM10污染水平时空分布及其与气象条件的关系[J].环境科学,2014,35(2):418-427.Zhao C X,Wang Y Q,Wang Y J,et al.Temporal and spatial distribution of PM2.5 and PM10 pollution status and the correlation of particulate matters and meteorological factors during winter and spring in Beijing[J].Environmental Science,2014,35(2):418-427.(in Chinese)

[9] 谢云峰,张树文.基于数字高程模型的复杂地形下的黑龙江平均气温空间插值[J].中国农业气象,2007,28(2):205-211.Xie Y F,Zhang S W.Spatial interpolation of mean temperature of Heilongjiang Province based on digital elevation model[J].Chinese Journal of Agrometeorology,2007,28(2):205-211.(in Chinese)

[10] 耿广坡,高鹏,吕圣桥,等.鲁中南山区马蹄峪小流域土壤有机质和全氮空间分布特征[J].中国水土保持科学,2011,9(6):99-105.Geng G P,Gao P,Lv S Q,et al.Spatial distribution of soil organic matter and total nitrogen in Matiyu small watershed in hilly area of middle southern Shandong Province[J].Science of Soil and Water Conservation,2011,9(6):99-105.(in Chinese)

[11] 张国峰,杨立荣,瞿明凯.基于地理加权回归克里格的日平均气温插值[J].应用生态学报,2015,26(5):1531-1536.Zhang G F,Yang L R,Qu M K.Interpolation of daily mean temperature by using geographically weighted regression-Kriging[J].Chinese Journal of Applied Ecology,2015,26(5):1531-1536.(in Chinese)

[12] 杨顺华,张海涛,郭龙,等.基于回归和地理加权回归Kriging的土壤有机质空间插值[J].应用生态学报,2015,26(6):1649-1656.Yang S H,Zhang H T,Guo L,et al.Spatial interpolation of soil organic matter using regression Kriging and geographically weighted regression Kriging[J].Chinese Journal of Applied Ecology,2015,26(6):1649-1656.(in Chinese)

[13] 四川省地方志工作办公室.四川年鉴2016[M].成都:四川年鉴社,2016:21-22.Office of Local Chronicles Compilation of Sichuan Province.Sichuan yearbook 2016[M].Chengdu:Sichuan Yearbook Press,2016:21-22.(in Chinese)

[14] Spreen W C.A determination of the effect of topography upon precipitation[J].Eos Transactions American Geophy- sical Union,1947,28:285-290.

[15] Smith R B.The influence of mountains on the atmosphere[J].Advances in Geophysics,1979,21(4):87-230.

[16] Odeh I O A,Mcbratney A B,Chittleborough D J.Spatial prediction of soil properties from landform attributes derived from a digital elevation model[J].Geoderma,1994,63:197-214.

[17] Juang K W,Lee D Y.A comparison of three Kriging methods using auxiliary variables in heavy-metal contaminated soils[J].Journal of Environmental Quality,1998,27(2):355-363.

[18] 张慧智,史学正,于东升,等.中国土壤温度的空间插值方法比较[J].地理研究,2008,27(6):1299-1307.Zhang H Z,Shi X Z,Yu D S,et al.Spatial prediction of soil temperatures in China using different methods[J].Geograp- hical Research,2008,27(6):1299-1307.(in Chinese)

[19] 王库.回归克里格在土壤全氮空间预测上的应用[J].中国农学通报,2013,29(20):142-147.Wang K.Application of regression Kriging on the spatial prediction of total soil nitrogen[J].Chinese Agricultural Science Bulletin,2013,29(20):142-147.(in Chinese)

[20] 曹祥会,龙怀玉,周脚根,等.河北省表层土壤有机碳和全氮空间变异特征性及影响因子分析[J].植物营养与肥料学报,2016,22(4):937-948.Cao X H,Long H Y,Zhou J G,et al.Analysis of spatial variability and influencing factors of topsoil organic carbon and total nitrogen in Hebei Province[J].Plant Nutrition and Fertilizer Science,2016,22(4):937-948.(in Chinese)

[21] Fotheringham A S,Charlton M E,Brunsdon C.The geography of parameter space:an investigation into spatial non-station- arity[J].International Journal of Geographical Information Systems,1996,10(5):605-627.

[22] Fotheringham A S,Brunsdon C,Charlton M E.Geographi- cally weighted regression:the analysis of spatially varying relati- onships[M].Chichester:John Wiley & Sons Ltd.,2002:16-24.

[23] Brunsdon C,Fotheringham A S,Charlton M E.Some notes on parametric significance tests for geographically weighted regression[J].Journal of Regional Science,1999,39(3):497-524.

[24] Akaike H.A new look at the statistical model identification[J].IEEE Transactions on Automatic Control,1974,19(6):716-723.

[25] McQuarrie A D R,Tsai C L.Regression and time series model selection[J].World Scientific,1998,42(2):480.

[26] Nakaya T,Fotheringham A S,Brunsdon C,et al.Geographic- ally weighted Poisson regression for disease association mapping[J].Statistics in Medicine,2005,24(17):2695-2717.

[27] 周长艳,岑思弦,李跃清,等.四川省近50年降水的变化特征及影响[J].地理学报,2011,66(5):619-630.Zhou C Y,Cen S X,Li Y Q,et al.Precipitation variation and its impacts in Sichuan in the last 50 years[J].Acta Geograph- ica Sinica,2011,66(5):619-630.(in Chinese)

[28] 邬伦,吴小娟,肖晨超,等.五种常用降水量插值方法误差时空分布特征研究:以深圳市为例[J].地理与地理信息科学,2010,26(3):19-24.Wu L,Wu X J,Xiao C C,et al.On temporal and spatial error distributions of five precipitation interpolation models: a case of Shenzhen[J].Geography and Geo-Information Scien- ce,2010,26(3):19-24.(in Chinese)

[29] 熊秋芬,黄玫,熊敏诠,等.基于国家气象观测站逐日降水格点数据的交叉检验误差分析[J].高原气象,2011,30(6):1615-1625.Xiong Q F,Huang M,Xiong M Q,et al.Cross-validation error analysis of daily gridded precipitation based on China meteorological observation[J].Plateau Meteorology,2011,30(6):1615-1625.(in Chinese)

Spatial Interpolation of Regional Precipitation Based on Mixed Geographical Weighted Regression Combined with Kriging Interpolation

LI Hao, LIU Tao, XU Jing-wen

(College of Resources Science and Technology, Sichuan Agricultural University, Chengdu 611130, China)

Based on the precipitation data of 1981−2010 from 144 meteorological stations in Sichuan province, using mixed geographical weighted regression Kriging interpolation (MGWRK) model, and considering the impact of topographic factors, the spatial distribution of the average annual precipitation was obtained in this paper. The effect of interpolation value was compared with those values from OK, GRK, and GWRK methods. The result showed that the optimal influencing factors combination was longitude, latitude and slope, determined by using the stepwise regression method, could decrease the multi-collinearity among the explanatory variables significantly. The types of spatial variability of the explanatory variables were analyzed quantitatively based on the index ΔAICc, which was the difference between the value of AICc (Corrected Akaike Information Criterion) of the same variable calculated by GWR model and by GR model. Then set the slope variable as global variable, and the longitude and latitude variables as local variables, the interpolation of the average annual precipitation in Sichuan province was conducted by the MGWRK model. The MGWRK method presented in this paper showed higher accuracy than those of the ordinary Kriging (OK) and global regression Kriging (GRK), because the method has taken into consideration of various influence factors of the spatial position and topography, and the variability of the relationship between these factors and precipitation.

Precipitation; Mix geographically weighted regression; Kriging interpolation; Spatial Interpolation

10.3969/j.issn.1000-6362.2018.10.006

李豪,刘涛,徐精文.基于混合地理加权回归与克里格的区域降水量空间插值方法[J].中国农业气象,2018,39(10):674−684

2018−02−08

国家自然科学基金项目（41501291）；四川省教育厅科研基金项目（14ZB0009）

李豪（1980−），博士，讲师，主要从事3S技术在水土资源可持续利用方面研究。E-mail: lihao@sicau.edu.cn