融合深度信息的Grabcut自动图像分割
2018-10-18石小龙漆坤元
刘 辉,石小龙 ,漆坤元,左 星
1(重庆邮电大学 通信新技术应用研究中心,重庆 400065)
2(重庆信科设计有限公司,重庆 400021)
1 引 言
图像分割的目的是通过自动或用户交互的方式将图像分成几部分的过程,是图像处理、人机交互等领域的基本问题之一,被广泛的应用于许多领域,来简化后续操作,如对象数据集构建[1],图像编辑[2]和图像检索[3]等.在众多图像分割方法中,基于图论的分割由于考虑了全局信息、能很好的融合颜色和区域信息、只需要少量的用户交互等优势而倍受关注[4].传统的图割是指采用用户交互方式手动将某些像素注释为前景对象和背景,并使用Graph-cut来完成对所有像素的标记[5].Grabcut[6]是这种方法的一种高级版本,它使用矩形边界框通过用户交互来表示前景对象,并采用三维高斯混合模型(GMM)来表示颜色统计的分布.其由于更高的分割精度和更简洁的用户交互而得到了广泛的应用,后续的研究也不断增多.
Tao等人[7]融合活动轮廓信息,优化了窄带图割算法.Hua等人[8]中,作者通两次交互的方式来初始化Grabcut,虽然增加了用户交互,但也提高了算法的分割精准度.He等人[9]用视觉显著性来初始化Grabcut,实现了图像自动分割,但不能有效处理对比度低的图片.Hu等人[10]以超像素代替像素来构建网流图,有效地提高了GrabCut算法的分割效率.以上改进在某种程度上都改进了Grabcut算法,但是在前背景差别不大时,Grabcut总是不能很好的分割,因为物体不仅有颜色、纹理等底层特征,在立体上也有特征定义,比如深度信息:能很好的表示出物体距离拍摄源的远近,这能很好的处理不同物体之间颜色相似、对比度低的情况.
近年来,随着强大的测距传感器的出现,RGB-D图像逐渐受到人们的关注.郑等人[11]通过自适应动态加权的方法来融合颜色和深度信息,并用MSRM进行区域合并,有效提高了图像分割的精度,但同一物体内特征变化大时,分割不好,而基于图论的分割算法会考虑全局信息从而克服基于聚类分割算法只会考虑局部信息的不足.Diebold等[12]通过将深度信息结合到能量公式中来改进Grabcut,但这种直接将深度作为GMM输入的第四个通道的方法没有很好地描述了图像内容的空间特性.Ling等人[13]通过重新定义深度惩罚项来改进Grabcut,并实现了边界细化,有效地提高了分割的精度,但该方法中深度惩罚项的权值固定,这在一定程度上增加了算法的复杂性.
针对以上问题,本文在显著性提取Grabcut矩形框的基础上,融合了深度信息.通过超像素处理来减少后续的计算,在此基础上生成显著图,并通过深度信息引导显著图来实现Grabcut的自动初始化,之后将融合的深度和显著性信息设计为动态约束项加入到能量公式中,最后进行Grabcut分割.
2 Grabcut自动分割算法
2.1 Grabcut算法
高斯混合模型(GMM)对颜色通道的估计具有很好的鲁棒性,因此Grabcut通过GMMs对颜色通告模型的估计,把分割问题转化为求每个像素不透明度的问题.将图像其表示为z=(z1,z2,…,zN),即求:

(1)
其中,α(α1,α2,…,αN),αn∈{0,1}表示像素的不透明度,像素点的αn值为0表示它属于背景,值为1表示它属于前景,这样分割也就是像素透明度的集合.除此之外,GrabCut有两个GMM,分别对应前景、背景.每个GMM由H个高斯模型混合而成(通常H=5),每个像素有一个参数hn∈(h1,…,hH),代表每个像素属于GMM中的第几个高斯函数.
通常GrabCut的吉布斯能量函数为:
E(α,h,θ,z)=U(α,h,θ,z)+V(α,z)
(2)
其中,数据项U定义为:
(3)
其中:D(αn,hn,θ,zn)=-logp(zn|αn,hn,θ)-logπ(αn,hn)且p(·)是一个高斯概率分布,π(·)是混合权重系数.
此时高斯参数模型为:
θ={π(α,h),μ(α,h),∑(α,h),α=0,1;h=1,…,H}
(4)
其参数分别对应第h个高斯模型的权值π、均值μ以及协方差∑.
平滑项V可用RGB空间的欧氏距离求出:
(5)
2.2 基于图论的显著性算法
图像显著性是对人类视觉注意机制的研究,能够有效提取出场景中感兴趣区域,因此图像显著性在计算机视觉,尤其在图像分割、目标识别等领域得到了广泛的应用.在图像分割中,图像显著性的研究对找到待分割区域有很大的帮助,而应用显著性的自动分割相对于无监督或半监督分割方法有着很大的优势.
对于基于显著性的图像分割,要先用显著性算法生成显著图,再通过显著图来引导后续的分割,因此,显著性算法的优劣对后续结果有很大的影响.一般用于图像分割的显著性算法有:RC算法[1]、GS_SP算法[14]、XIE算法[15]等.本文选取的是Yang[21]提出的基于图论的流形排序的显著目标检测,与其他算法不同的是:该算法以SLIC超像素分割算法对图像做预处理,而本文也同样用SLIC算法;且在计算显著性时,由于同时考虑了前景和背景线索,面对处于边缘的感兴趣区域也有很高的鲁棒性,因此有很好的查准率、查全率和Fβ.
该方法以超像素代替像素,分别以上、下、左、右边缘的超像素为线索来生成显著图,再以该显著图为线索生成最终的显著图.先构造单层图G=(V,E),其中V为节点,E为无向边,定义两个节点之间的权重为:
(6)
其中ci和cj表示两个节点的颜色值,σ为权重系数.以边界上的节点为依据,并用一个排序函数来对整张图的超像素进行排序.排序公式为:
f*=(D-βW)-1q
(7)
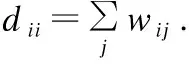
以图像上侧超像素为依据,通过对其他超像素排序来得到显著图St:
(8)
式(8)中后一项为归一化向量.同理,用该公式计算其它三侧的显著图Sb、Sl、Sr. 整合4个显著图来得到第一步的显著图.
Sbq(i)=St(i)×Sb(i)×Sl(i)×Sr(i)
(9)
以第一步的显著图的平均显著值为阈值,通过阈值分割将其分为二值图,并以此为图像中心为依据,用同样的方法求出最终的显著图:
(10)
2.3 结合显著性的Grabcut自动分割
得到显著图后,一般通过一个给定的阈值来对图像进行二值分割,进而确定用来初始化Grabcut的矩形框.但由于本文算法在超像素的基础上进行,所以做出了一些改变:只需要针对每个超像素的代表值,而不是针对每一个像素值.具体阈值为:
(11)
其中,Num为超像素的实际数目,S(i)为第i个超像素的显著值.假设显著值大于T的为前景,重置为1,而小于T的为背景,重置为0.我们从上至下依次扫描像素点,通过标记第一个非0像素点来得到Grabcut的初始矩形框.
3 融合深度信息的Grabcut自动分割算法
本章详细介绍了本文改进算法的重点部分.首先,为了更好的融合深度信息,在对Grabcut算法做改进之前,先对矩形框提取部分做了改进,不仅仅通过显著性来找出矩形框,还加入一个深度信息的引导,增加矩形框提取的准确性;其次,本文对Grabcut算法的能量函数做了改进,通过深度信息的融入,有效提高算法的分割精度.
3.1 矩形框的提取
在2.2中,本文用基于图论的流行排序算法来生成显著性图,从而得到Grabcut的初始化矩形框.而在本节,为了更好与深度信息结合起来,将该算法有效的扩展到RGB-D图像上,将以深度信息为指导来生成Grabcut矩形框.
由于本文涉及的算法都是在SLIC的预处理下进行的,所以我们要对深度图做相应的处理:不是直接对深度图进行SLIC分割,在原图进行SLIC的基础上,将其对应的深度图也分割为对应的超像素区域.并以一个区域的深度信息的平均值代替该超像素内所有像素的深度信息进行下一步处理.
在视觉感知和认知心理学中认为,我们观察到的深度是基于越接近的物体会吸引越多的注意力. 然而,Lang等人[16]指出,深度和显着性之间的关系是非线性的,不同景深(DOF)图对应的显著性和深度的关系不同,即当场景或者图片有不同的DOFs时,显著的对象可能出现在不同的位置,因此Lang等用高斯混合模型来学习深度先验信息.为了简化计算,本文参考Ren等[17]提出的方法:将每幅图像中的绝对深度值重新调整到[0:1]的范围内,来去除DOF的影响.Ren等人通过最大化后验概率P(S|D):
(12)
来求出深度信息对显著性的影响,并最终使用以下形式来估计深度先验图:

(13)
其中,d(i)是第i个超像素的深度值均值,这个公式大致适合后验分布,仅仅在较近的距离上有一个小的偏差,具体可参考[20].
在对深度图进行处理后,用归一化的深度信息指导的显著性来进行下一步的计算:
Ssd=S(i)*D(i)
(14)
其中Ssd(i)为第i个超像素结合深度和显著性后的信息.我们将Ssd(i)代入(11)即可得到Grabcut矩形框.
3.2 能量函数的改进
在本文的预处理过程中,我们同时利用了显著信息和深度信息,并通过用深度信息指导显著信息的方式生成矩形框.鉴于此,为了有效利用这些信息,没有使用深度信息D来改进Grabcut能量公式,而是用深度信息指导的显著信息Ssd来进行改进.
在以往融入深度信息的方法中:文献[11]直接将深度作为GMM输入的第4个通道、文献[12]融入深度惩罚的权值固定.这些方法或者没有充分利用深度信息,或者加大了算法的复杂性,为了改善这种情况,本文分别改进了能量函数总的数据项和平滑项,并分别用前背景GMMs的相对熵(KL距离)以及像素之间的相似性来计算区域项以及边缘项中Ssd惩罚项的自适应权重.
3.2.1 对数据项的改进
在Grabcut中,GMMs估计对颜色通道具有很好的鲁棒性,且理论上GMMs可以逼近任何概论分布,因此论文[11]直接将深度信息作为GMMs的第4通道进行计算.
为了更好的利用Ssd信息,本文对Ssd进行GMMs估计,与对颜色的估计相同,Ssd的数据项函数为:
(15)
其中,d为每个超像素的深度信息,其他与原数据项一致
(16)
此时,需要求得参数有:前背景的第h个高斯模型的权值π、均值μ以及协方差∑.
为了有效地将Ssd信息融合到Grabcut的数据项中,用相对熵对数据项进行改造,计算颜色GMM的KL距离以及SdGMM的KL距离,根据[18],两个GMM之间的KL距离为:

(17)

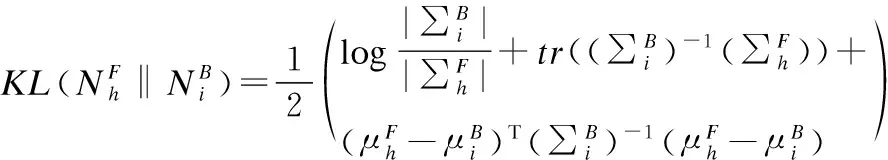
(18)
由此可以计算出Ssd数据项的自适应权重:
(19)
即权重由颜色和Ssd共同决定,当颜色差别较大时,主要由颜色决定分割;当颜色差别较小时,主要由Ssd决定分割.
3.2.2 对平滑项的改进
Grabcut的平滑项主要是通过计算颜色的欧氏距离来决定,基于此,同样使用Ssd的欧氏距离来改进平滑项:

(20)
与数据项的自适应权重相似 ,平滑项的自适应权重为:
(21)
综合上述改进,最终的能量公式为:

(22)
最后,参考文献[10],由于超像素分割没有融合深度信息,所以在基于超像素的网流图上迭代好参数后,再在原图上进行分割,来弥补超像素分割的不足.
综上所述,改进的Grabcut算法流程为:
1) 对给定的图像进行SLIC超像素分割,并构建单层图,利用流行排序算法来得到超像素的显著值.
2) 对深度图进行对应原图的超像素分割,分别用公式(13)和公式(14)来处理深度信息和显著信息,并由此产生二值图来初始化Grabcut算法;.
3) 用超像素图构建Grabcut的网络流图,并在 2) 的基础上进行初始化,其中,将框外定为背景TB,框内定为未知区域TU,而此时前景为空.依次来此估计GMM参数:其中第k个高斯模型的均值μ(α,h)、协方差∑(α,h)和权重π(α,h).
4) 利用改进的公式(22)来计算网络流图的边的权值,进行最大流/最小割.
5) 计算能量函数,判断能量函数是否收敛,若不收敛,则重新计算GMM参数,并返回4);若收敛,则下一步.
6) 以像素点为单位,用上一步的GMM参数为基础,进行最大流/最小割.
4 实验结果及分析
为了验证本文算法的有效性,在RGB-D图像库上进行了实验分析,该图像库包含1000张RGB图像、对应的深度图以及Ground-truth,实验的平台为:64位Windows 7,Matlab 7.0,Microsoft Visual Studio 2013,CPU:i5 2400,RAM:4GB.在进行实验分析前,先对参数进行说明:在图像预处理阶段,本文用了SLIC算法,其中超像素数量为1000、m为20;而显著性算法中,σ2=0.1以及β=0.99.
4.1 实验分析
本文实验步骤大致可分为:SLIC分割、显著图、融合深度信息的显著图、二值分割图、Grabcut分割图.依次输出以上图像,来验证本文算法的可行性.图1为本实验涉及的效果图.

图1 实验步骤实例Fig.1 Example for experimental steps
如图1所示,图1(a)为RGB原图,图1(b)为对应的深度图,先对原图做SLIC超像素分割,得到图1(c);再以图1(c)为基础构建单层图,得到显著图图1(d);然后在原SLIC的基础上,对深度图进行分割得到图1(e);以深度图1(e)指导显著图1(d)从而得到最终的Ssd图1(f);根据公式(10)进行二值化,得到Grabcut矩形框图1(g);最后进行Grabcut分割得到图1(h).
4.2 对比实验
为了进一步验证本文算法的有效性,分别于Grabcut、SLIC-Grabcut[10](一种用SLIC预处理来加速Grabcut的算法)、DGS-Grabcut[19](利用深度信息来初始化Grabcut,并将深度信息作为GMM第四通道来融入Grabcut)、VSM-Grabcut[20](利用显著信息来初始化Grabcut,并以固定阈值的方式将显著信息融入Grabcut的能量公式中),从分割效果、精准度、分割时间3个方面进行比较.
4.2.1 分割效果
如图2所示,从图2(a)到图2(g)分别对应原图、深度图、Grabcut、SLIC-Grabcut、VSM-Grabcut、DGS-Grabcut以及本文算法的分割效果图.以吊灯为例,总的来说,5种算法图中,图2(c)和图2(d)由于只用颜色没有加入任何信息,所以当前景和背景颜色相近时,分割效果就有所欠缺,而图2(e)和图2(f)由于融入了显著和深度信息,所以分割效果也相对理想.但是,显著信息和深度信息有所偏差时,也不能很好的得到有效的前景,比如雕塑的图2(e)中,背景的黑色区域被提取为显著目标,从而影响了最终分割结果;而在椅子的图2(f)中,由于椅面比椅腿相对靠前,使其融入深度信息的分割结果中没有了椅腿,当然是否需要椅腿也是根据后续工作来定的;安全指示灯(EXIT)的分割结果虽然有所不同,但由于前背景颜色信息相差很大,所以相对来说都有比较好的分割结果;在大钟的分割对比中,由于深度信息要比颜色和显著信息更能表示前背景的差距,所以图2(f)和图2(g)的分割效果较好.

图2 不同算法的分割结果对比Fig.2 Segmentation result comparison of different methods
4.2.2 分割精准度
为了进一步验证本文算法,从分割精度方面来度量分割的效果.分割精准度P为:
其中,CB为正确的背景像素,CF为正确的前景像素,N为总像素数.表1为各个算法对应图片的精准度(%).
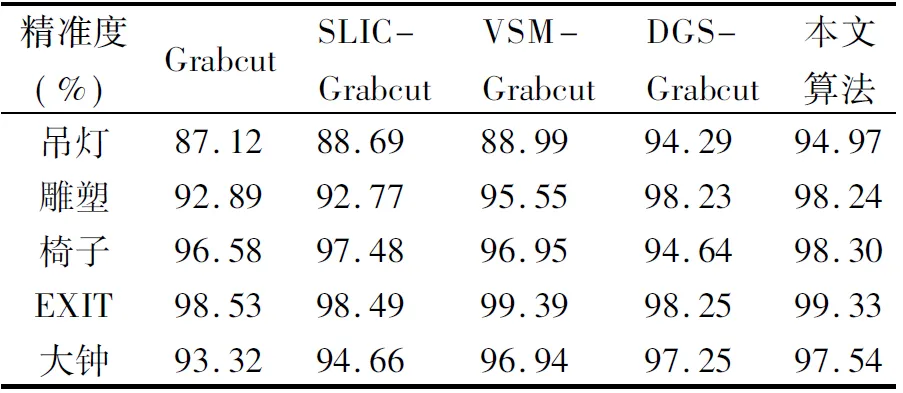
表1 不同算法的分割精准度对比Table 1 Precision comparison of different methods
由表1可看出:本文的精准度要普遍高于其他算法;在前背景颜色相差较大时,Grabcut以及其他算法都有较好的分割效果;而在前背景对比度低时,融合显著信息或深度信息的DGS-Grabcut和VSM-Grabcut算法的分割效果要优于原Grabcut算法.
4.2.3 分割时间
虽然传统的Grabcut拥有较好的分割精准度,但由于迭代GMM的原因,其分割时间一直是影响其分割效率的重要因素之一.因此,本文以SLIC超像素分割作为算法的预处理过程,来提高其分割效率.表2为各个算法对应图片的分割时间对比.
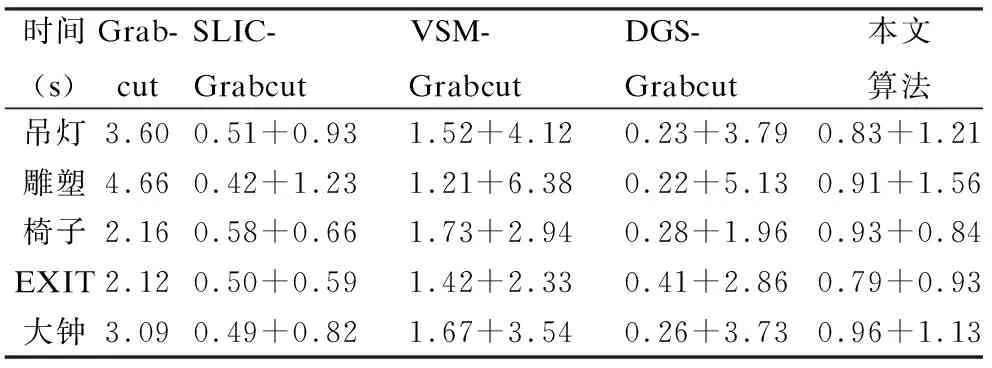
表2 不同算法的分割时间对比Table 2 Run time comparison of different methods
如表2所示,其中,除了Grabcut以外,其他算法都需要预处理时间:SLIC-Grabcut中,需要先把图像分割为超像素,以超像素为节点进行图的构建,不过有效减少了后续分割时间;DGS-Grabcut中,先通过处理深度图像来得到Grabcut的初始化信息;VSM-Grabcut中,需要先求出图像的显著性,在通过显著信息得到Grabcut初始化信息;而本文算法的预处理过程除了将原图分割为超像素、求出显著信息外,还需要融合深度信息并求出Grabcut的初始化信息,预处理步骤相对多.但是由于本文算法以超像素为节点构建单层图(显著图模型)和网流图(Grabcut图模型),所以整体分割时间也在合理范围内.
5 结束语
随着计算机视觉及图像处理的要求越来越高,以及深度传感器和双摄像头的普及,深度信息也越来越受关注.本文以超像素为节点构建网流图,通过深度指导显著信息来初始化Grabcut信息,并利用结合的深度信息来改进Grabcut的能量公式,有效地将深度信息融入到结合显著性的Grabcut自动分割框架中.实验表明,本文算法提高了Grabcut的分割效率和分割精准度,可以有效地分割对比度低的前背景.
