基于动态干涉仪的位相光栅衍射效率研究
2018-10-17
(福州石径信息技术有限公司 福建 福州 350000)
一、引言
光栅是现代光学中的重要光学元件,按照光栅刻蚀微结构可分为矩形光栅、正弦光栅及其他不规则形状光栅,按刻蚀深度又可以分为二级、三级至多级光栅,其中最广泛使用的是矩形二级光栅。
光栅作为良好的分光器件及光束复制器件,越来越多地使用在干涉测量中。从光栅用于朗奇检验以来,多种剪切干涉测量技术使用光栅作为剪切干涉的分光器件[1~3]。在时域移相干涉测量中,光栅也经常作为移相器件[4]。在空域移相干涉测量中,二维光栅是经典的分光器件[5~8]。
在动态干涉仪中[5~8],二维光栅作为分光器件,通常选取为(±1,±1)级衍射光,往往出现能量不足的问题。除此之外,光栅的其他级次衍射光不参加干涉,这样大大浪费了透射光的能量。由于位相光栅可以抑制其他级次的衍射光,所以比振幅型光栅更适于作为分光器件。基于电磁场理论的矢量分析法是系统而全面的光栅衍射效率分析方法[9],在此基础上,K.Knoph[10]和L.Li[11]对一维位相光栅进行了分析,Soon Ting Han[12]和Lifeng Li[13]对二维位相光栅进行了分析,对于周期达波长及亚波长级的高频光栅,电磁矢量分析可以针对不同的偏振模式进行分析,且精度很高,但是过程相对复杂。对于周期为波长10倍以上的光栅,可以采用标量衍射分析[14]。在最近的研究中,Xufeng Jing[15]指出周期为波长4倍以上时,标量衍射理论已能满足分析要求。上述文章只分析了不同周期大小(相对波长)的普通位相光栅各衍射级次的计算误差,旨在探索标量衍射的适用范围极限,没有针对实际应用需求或针对特定衍射级次进行分析,也没有设计相应的光栅来改变特定衍射级次的衍射效率。
本文针对动态干涉仪二维分光光栅的实际应用需求,研究二维光栅衍射效率,设计了一种棋盘型位相光栅。动态干涉仪中使用的二维光栅频率较低,周期一般为几十微米,而且只对透射光的(±1,±1)级衍射光有所要求,因此文中采用标量法分析光栅衍射效率。为了与棋盘位相光栅对比,选取常用的正交位相光栅,分析了两种类型位相光栅的衍射效率与刻蚀深度的关系,给出了最佳刻蚀深度,使(±1,±1)级光衍射效率最大化。在试验中将正交位相光栅与棋盘位相光栅做了应用对比。
二、原理
设位相光栅的振幅透过率为1,单位振幅平面波入射到光栅表面,其透射波面复振幅可写为
A(r)=exp(-ik·r)=exp(-i(kxx+kyy+kzz)).
(1)
其中k、kx、ky、kz分别表示波矢及xyz方向的波矢分量。若入射波面垂直光栅表面,则有kx=0,ky=0,A=exp(-ikz),光栅衍射光强就可以表示为透射函数的平方。光栅的基片厚度除了在干涉测量中带来像差之外并不影响光栅衍射效率,因此在下面的光栅衍射效率分析中将忽略基片厚度。
(一)矩形正交位相光栅衍射效率
常见的正交位相光栅结构如图1所示,Λx和Λy分别表示x和y方向的光栅周期。考虑单个周期单元,φu(x,y)表示一个单元内的相位分布,单元透射函数tu(x,y)可表示为:
(2)
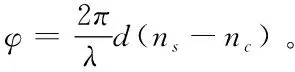
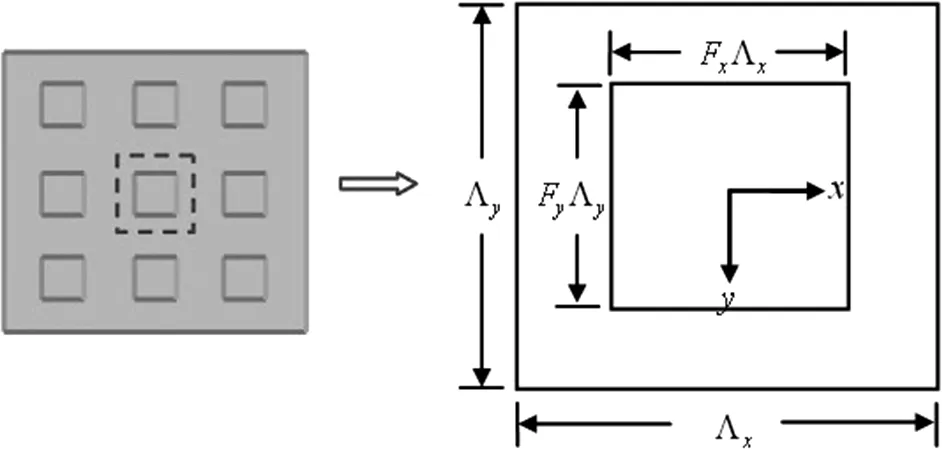
图1 常见矩形正交位相光栅的周期单元
整个光栅的透射函数t(x,y)可写成
(3)
其中,符号*为卷积运算符,comb为梳状函数,根据梳状函数及矩形函数傅里叶变换性质,对光栅透射函数进行傅里叶变换有:
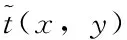
(4)
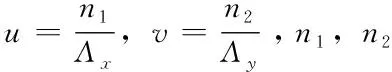
(5)
在透射光中,(n1,n2)级衍射光的衍射效率可表达为:
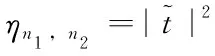
(6)
(二)棋盘位相光栅衍射效率
棋盘位相光栅(如图2所示)指的是光栅微结构呈国际象棋棋盘状分布的矩形结构位相光栅。在光栅一个周期单元内,使用矩形分割方法将光栅周期单元划分为2×2个面积相同的矩形块,光栅脊厚用d表示,且占空比Fx和Fy值固定,为Fx=0.50和Fy=0.50。棋盘位相光栅一个周期单元的透射函数tu(x,y)为:
(7)
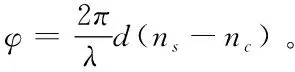
(8)
对透射函数进行傅里叶变换有:
(9)
同理,各级次衍射效率为:
(10)
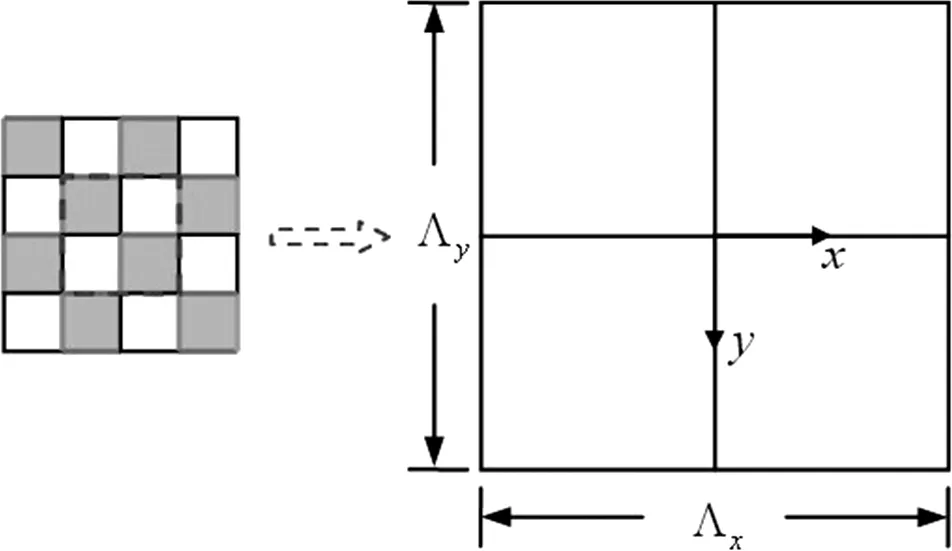
图2 棋盘位相光栅周期单元
三、仿真与分析
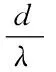
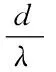
在动态干涉仪中需要四支衍射效率相同的(±1,±1)衍射光,图(d)中,当相位延迟为π,占空比Fx=Fy=0.5时,有(±1,±1)光衍射效率最大值。此时,(0,0)级衍射光为25.00%,(0,±1)级和(±1,0)级衍射效率为10.13%,(±1,±1)衍射效率为4.11%。此时,(0,0)级衍射光依然很强,浪费了大量的光能量。
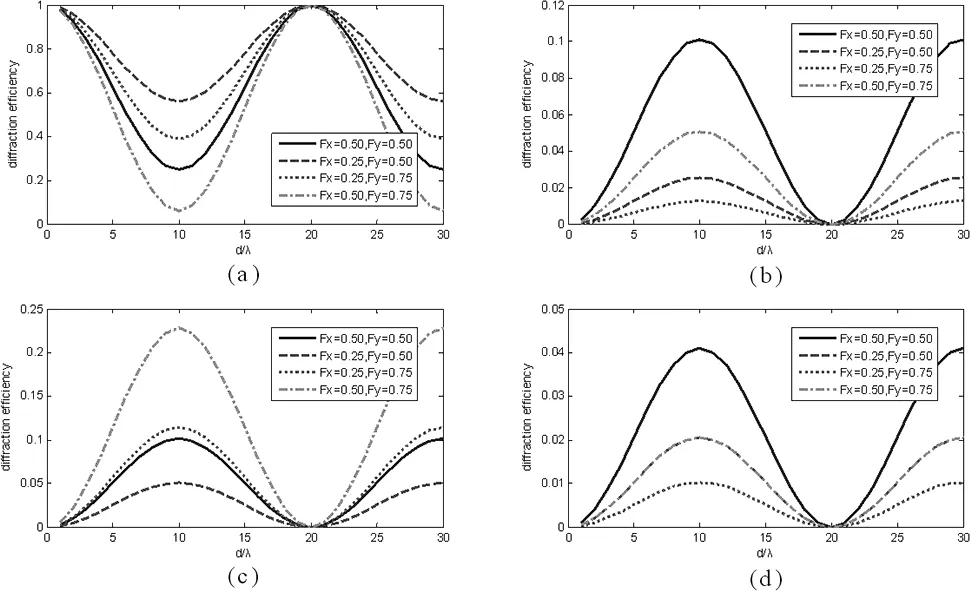
图3正交位相光栅衍射效率与刻蚀深度关系。(a)(0,0)级,(b)(0,±1)级,(c)(±1,0)级,(d)(±1,±1)级
Fig.3Relationbetweendiffractionefficienciesandetchingdepths.(a)(0,0)thorder,(b)(0,±1)storder,(c)(±1,0)thorder,(d)(±1,±1)storder
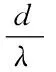
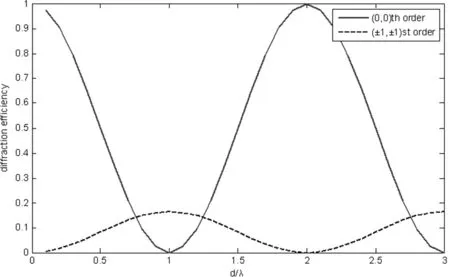
图4 棋盘位相光栅衍射效率与刻蚀深度关系
Fig.4Relationbetweendiffractionefficienciesofphasechessboardandetchingdepths
四、实验
动态干涉仪光路图如5所示,其主要组成器件为:激光器、半波片(G1)、扩束系统、偏振分光棱镜(PBS)、1/4波片(G2~G4)、参考面、被测球面、二维分光光栅、透镜组、空间光阑、偏振片组及CCD像机。其基本原理为:使用二维光栅分光,用空间光阑滤出(±1,±1)级衍射光,经偏振片组使其同步移相,得到四幅移相干涉图,用四步移相法恢复面形。由于抗震需求,其CCD工作时需要高帧率、低曝光条件。
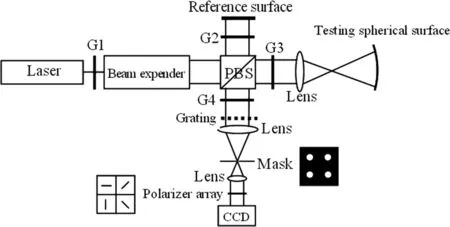
图5 动态干涉仪光路图
在动态干涉仪分光光栅设计过程中,先后设计并刻蚀了正交位相光栅和棋盘位相光栅。两种光栅都针对波长为632.8 nm设计,其中正交位相光栅占空比为Fx=Fy=0.5,基底材料为K9玻璃,折射率为1.516,光栅周期为40 um,刻蚀深度设计为608.5 nm,棋盘位相光栅基底材料为熔石英,折射率为1.461,光栅周期为50 um,刻蚀深度设计为690 nm。
如图6给出用Veeco公司的白光轮廓仪分别对两种光栅微结构的测量结果,图(a)显示的是二维正交位相光栅的表面轮廓,其刻蚀深度的实测结果为610.1 nm,图(b)显示了棋盘位相光栅的表面轮廓,其实际刻蚀深度为711.8 nm。
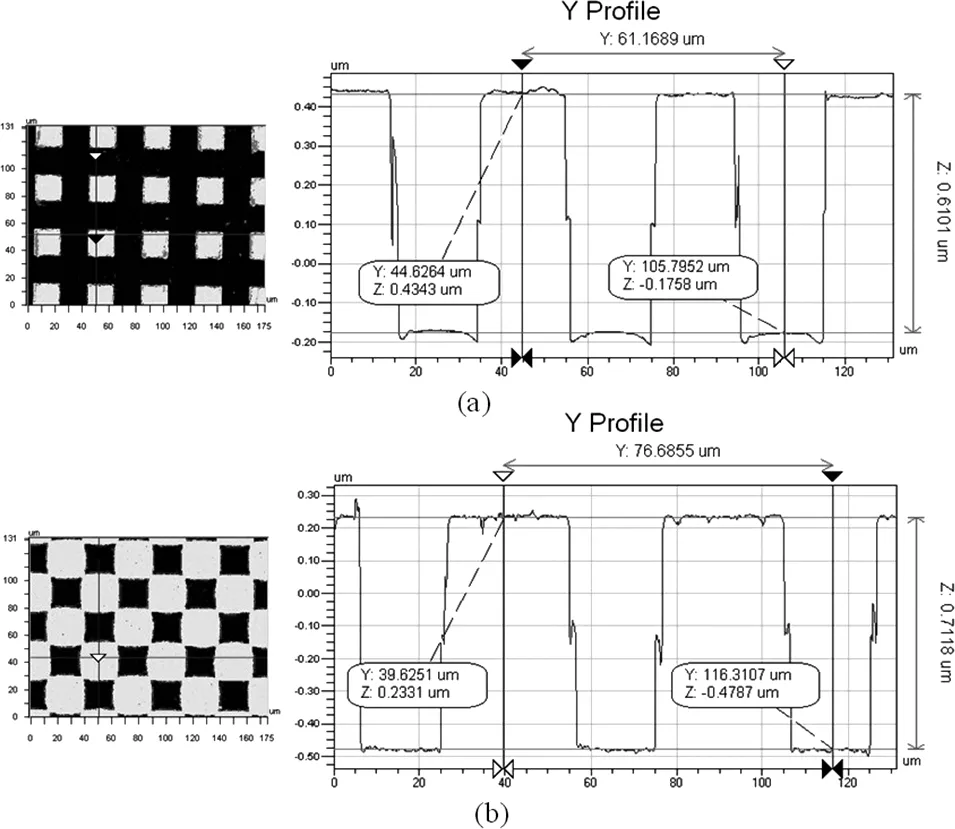
图6 两种光栅的轮廓测量。(a)二维正交位相光栅;(b)棋盘位相光栅
Fig.6Profilemeasurementsofthetwogratings.(a)two-dimensioncrossphasegrating;(b)phasechessboard
将两种光栅用于动态干涉仪中,两种光栅都选取(±1,±1)级四支衍射光,保持CCD采集条件相同,采集到的同步移相干涉图如图7显示,图(a)为正交位相光栅的应用效果,图(c)为棋盘位相光栅的应用效果。对比两图,从直观上可以看出正交位相光栅得出的干涉图较暗、不清晰,明显能量不足,而棋盘位相光栅效果较好。图(b)为用正交位相光栅得出干涉图组中单幅干涉图的灰度直方图,图(d)为用棋盘位相光栅得出干涉图组中单幅干涉图的灰度直方图。对比灰度直方图,(b)图中灰度值集中在40以下,亮条纹与暗条纹灰度值相差较小,导致条纹对比度较低;(d)图中灰度值最大达到190,亮条纹与暗条纹灰度值相差较大,条纹对比度较高。

图7两种光栅用于动态干涉仪的效果(a)正交位相光栅得到的干涉图组,(b)正交位相光栅得到干涉图的灰度直方图(b)棋盘位相光栅得到的干涉图组,(d)棋盘位相光栅得到干涉图的灰度直方图
Fig.7Resultsofthetwokindsofgratingsappliedtodynamicinterferometer.(a)interferogramsbycrossphasegrating,(b)grayhistogramofinterferogrambycrossphasegrating,(c)interferogramsbyphasechessboard,(d)histogramofinterferogrambyphasechessboard.
五、结论
本文根据动态干涉仪光能量实际需要,分析对比正交位相光栅与棋盘位相光栅的衍射效率,结果表明棋盘位相光栅不仅抑制了(0,0)级,还抑制了(0,±1)级和(±1,0)级,其四支(±1,±1)级衍射光总的衍射效率为正交位相光栅的4倍。棋盘位相光栅应用在动态干涉仪上得到的干涉图对比度相较于正交位相光栅有着显著的提高,更适于作为动态干涉仪的分光器。
