基于Fluent对旋流沉砂池的数值模拟
2018-10-17周士雄
周士雄
(晋中市榆次区水利局,山西 晋中 030600)
1 概况
旋流沉砂池作为城市处理厂必不可少的处理设施,因具有占地小、效率高、能耗低和运行可靠等优点受到了国内外污水处理界的重视[1]。根据池底设计成水平还是斜坡形式,把旋流沉砂池分为比氏和钟氏两种形式。对于钟氏沉砂池,由于斜坡作用可以依靠重力对沙粒进行沉降;氏沉砂池由于没有斜坡作用,主要依靠进水、叶片的高速旋转等形成强制涡旋,使得砂粒往沉砂池中心移动。
栾闯[2]于2009年利用CFD对沉淀池进行数值模拟,并在传统的旋流沉砂池的理论基础上进行优化,得到新型高效旋流沉砂池,优化后的旋流沉砂池不仅保持了原来沉砂池除砂率高的特点,同时还具有桨板维修方便、清渣更为彻底、节能的特点。何航[3]于2011年通过数值模拟,得到沉砂池内部的速度矢量图,压力云图,颗粒轨迹图,进而分析进水速度和进水颗粒物浓度对除砂率的影响。和笑天等[4]于2014年发明的旋流沉淀池,主要综合比式沉砂池和钟式沉砂池各自的优点,并在此基础上加以改进,使新设计的沉砂池具有节省占地面积、结构简单、处理效果好等优点,这种新型沉砂池目前在我国污水预处理工艺中应用广泛。王雪原[5]在研究比氏旋流沉砂池中指出,搅拌桨的运行及调整对池内的水平环流没有调节作用,因此,控制沉砂池进水流速是影响沉砂池处理效果的关键因素;当进水流速太大时,沉降砂粒很大几率被带入出水口;当进水流速太小,砂粒则可能在渠道内逐渐沉积下来,不利于沉砂池的运行。
本文以比氏旋流沉砂池为研究对象,采用标准k-ε模型和Multiple Reference Frame (简称MRF)模型,利用Fluent软件对2D和3D旋流沉砂池进行数值模拟,主要研究了压强、速度和速度矢量对沉砂池产生的影响。
2 数值模型
对于流体的运动过程采用连续性方程、动量方程、湍动能输运方程和湍动能耗散率输运方程来描述[6]。
2.1 连续性方程
式中 t为时间;ρl为流体相的密度;ul为流体相的瞬时速度。
2.2 动量方程
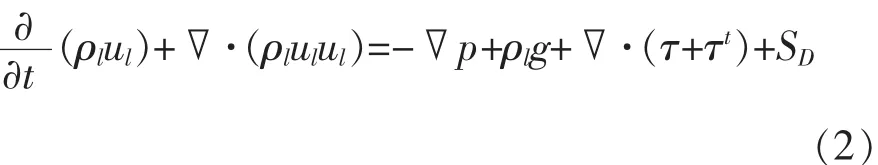
式中 t为时间;ρl为流体的密度;ul为流体的瞬时速度;g为重力加速度;p为压强;τ为流体层流应力;τt为湍流应力,为动力黏度;I为湍流强度;ρl为流体的密度;k为湍动能;SD为动力源项。
2.3 k-ε方程
湍动能k方程:

湍动能耗散率ε方程:
式中 ρl为流体的密度;k为湍动能;xj为j方向坐标;uj为j方向速度;μj为动力黏度;μl为分子黏度;σk为常数[7];P为瞬时压力值;ε为湍流耗散率;ui为i方向速度;ul为流体的瞬时速度;xi为笛卡尔坐标系下3个方向的分量;σε为常数[7];Cε1,Cε2为经验系数[7]。
3 模型概况
3.1 2D旋流沉砂池模型建立及网格划分
在旋流沉砂池进行分析时可将问题简化成2D模型,这样在减少计算量的同时还能达到对问题有效的求解。模型尺寸为:螺旋桨叶片宽1m,长2m;内部圆形动网格区域半径3.5m;圆形池体半径6.5m;水流入口宽度2m;出口宽度2m。
网格划分对计算流体力学(CFD)非常重要,网格的质量直接影响到数值模拟的结果,网格质量的提高往往能节省计算的时间和得到更加精确的求解。Fluent求解器在对模型进行求解,即利用计算机将控制方程在空间区域进行离散,然后得到离散方程;网格上的节点就是求解位置物理量的位置,计算机在对控制方程离散的过程将物理量的定义储存在这些节点上。在对2D旋流沉砂池网格划分的过程中采用结构网格和非结构网格结合的方法,在划分网格时,将沉沙池体内部圆形运动区域附近的网格进行局部加密(动网格区域内部网格Δx=0.05,其他区域网格Δx=0.1),网格总数约2.5万个。模型的尺寸和网格划分的形式如图1。

图1 2D沉砂池模型与网格划分
3.2 3D旋流沉砂池模型建立及网格划分
3D旋流沉砂池构造上由一个圆柱形池体、搅拌桨、矩型进水渠、矩型排水渠、一个圆柱形运动区域构成。池体半径3.65m,高4.1m;圆形运动区域半径1.8m,高4.1m;沉砂池的进水渠与池体底部相平,外侧边缘与池壁相切,进水渠宽2m,高2.3m;出水渠底部与进水渠顶部同高,顶部与池体顶部向平,外侧边缘与池壁相切,出水渠宽2m,高1.8m;搅拌器中心圆柱体半径0.55m,高0.4m;叶片长1.1m,宽0.4m,高0.1m,每个叶片沿轴向插入圆柱体0.1m;搅拌器中心距离池底0.4m。对于3D旋流沉砂池采用非结构网格进行划分,对于圆柱池体以内网格进行局部加密(Δx=0.1),进出水渠部分的网格相对稀松 (Δx=0.2),网格总共49万个,最后选取z=0.6m处的网格,如图2。

图2 3D旋流沉砂池模型与网格划分
4 结果分析
4.1 2D旋流沉砂池
4.1.1 压力场分析(2D)
沉砂池压力场云图如图3。
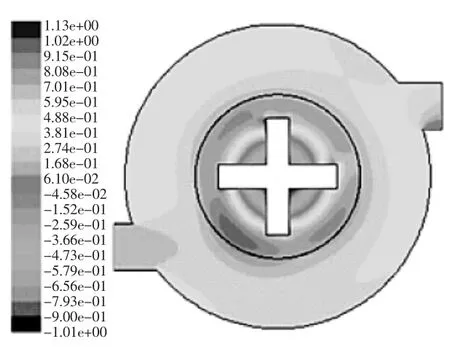
图3 2D旋流沉砂池压强云图
从图3可以看出,从沉砂池池壁向中心压强在减少,也即池壁边缘附近的压力大于沉砂池中心处压强,这样会产生压力差使得随水流流入池内的砂粒在压力作用下向池中心集中。值得注意的是在整个压力云图中,搅拌区域叶片处的压强达到最大,而在沉砂池中心的压强较小,这种高压力差可以进一步使得聚集在沉砂池搅拌区域的砂粒往中心聚集,最终在池中心沉降下来。计算区域中入口出压强较出口处压强大,从流体力学分析可知,流体从压强较大处流向压强较小处,为了使入口的液体向出口流出,入口处压强势必要比出口处的大。
4.1.2 速度场分析(2D)
沉砂池速度场云图如图4。

图4 2D旋流沉砂池速度云图
从图4可以看出,沉砂池水流速度从池壁向中心径向逐渐减小,搅拌区域速度大小相差不大,沉砂池中心部分区域速度值为0,出口区域附近速度大于入口速度,这与压强分析的结果保持一致原则。搅拌区域处流体速度大小差距甚小,在高速旋转的叶片作用下池体内部水流始终保持环流流动;水流速度从池壁向中心速度在减少,搅拌区处的流体在叶片的作用下与叶片保持相同的角速度绕流,在角速度相同的情况下半径越大速度越快,进入池体内的水流和砂粒由于受到不同的速度而被分开。从伯努利方程出发可知,压强与速度成反比;对沉砂池入口和出口进行分析,入口处压强大于出口处压强,那么入口速度小于出口速度,符合伯努利方程;但是从沉砂池内部看,水流速度从池壁向中心速度在减少,不符合伯努利方程,导致这种情况的原因可能是沉砂池中叶片的转动产生的切向、径向、轴向的速度对周围产生了很大影响。
4.2 3D旋流沉砂池
4.2.1 压力场分析(3D)
图5和图6分别是Z=0.6m,Z=3.8m和Y=-2.65m处的压力云图。其中,Z=0.6m是搅拌区域叶片中心位置处的截面,通过对这个截面分析可以看出叶片的高速转动对沉砂池的影响;Z=3.8m处的截面是接近水面处的一个截面;Y=-2.65m是在进出水渠中心处的截面,通过这个截面我们可以看到进出口渠附近的流动状态。

图5 Z=0.6m和Z=3.8m处压强云图

图6 Y=-2.65m处压强云图
从图5可以看出,3D旋流沉砂池在进水渠处压强最大,当水流流入池体后,压强从池壁往沉砂池中心呈现不断减小的趋势,尤其在出水渠处压强最小。分析可知,水流沿切线进入沉砂池后在压力作用下绕池体中心做圆周运动,随后沿切线从排水渠中流出。
对比图5和图6可知,沉砂池底部压力大于沉砂池上部压力,由于沉砂池内上下部形成的压力差,导致进入沉砂池中的水流自下而上流动,而一些相对密度大的砂粒在重力作用下逐渐下沉,与水流分开。
4.2.2 速度场分析(3D)
从图7中可以看出,水流在进入沉砂池后在入口处流速较大,随着搅拌叶片的转动,水流在沉砂池中做圆周运动。与2D旋流沉砂池分析结果一致的是水流速度从池壁向中心速度在不断减少,由此可以推断出砂粒随水流做旋流运动,随着时间的增长,砂粒逐渐往池体中心靠拢,最终在中心沉淀池中沉淀下来。
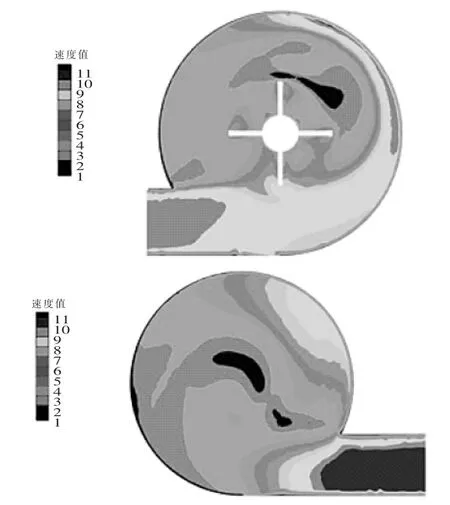
图7 Z=0.6m和Z=3.8m处速度云图
4.2.3 速度矢量分析(3D)
通过Fluent求解器得到Z=0.6m,Z=3.8m和Y=-2.65m处截面的速度矢量图,如图8和图9。

图8 Z=0.6m和Z=3.8m处速度矢量图

图9 Y=-2.65m处速度矢量图
从图中可以看到,水流在沿池壁切线方向进入沉砂池,在沉砂池中旋转运动一圈后从相对一侧的边壁切线方向流出,在池体中形成漩涡。涡流的形成主要受两方面影响,一方面由于水流沿切线进入沉砂池时受到池壁的阻挡,另一方面搅拌器叶片的旋转使流体形成以搅拌器叶片为中心的圆周运动。在Y=-2.65m截面(图9)的速度矢量图中可以看到水流是自下而上流动,导致一些相对密度较小的砂粒在沉降过程中被水流卷起和水流一起流出。
5 结语
(1)通过利用ICEM对2D和3D旋流沉砂池进行建模,利用Fluent求解器对模型进行计算,利用CFDPost进行后处理。主要从2D和3D旋流沉砂池的压强和速度等参数进行分析,系统研究了旋流沉砂池的工作原理和流场分布状态。
(2)不论2D还是3D,旋流沉砂池压强在进水渠处最大,当水流流入池体后,压强从池壁往沉砂池中心呈现不断减小趋势,尤其在出水渠处压强达到最小。
(3)2D和3D旋流沉砂池水流速度从池壁向中心速度在不断减少,由此可推断出砂粒随水流做旋流运动,随着时间增长,砂粒逐渐往池体中心靠拢,最终在中心沉淀池中沉淀下来。
(4)从3D旋流沉砂池的Y=-2.65m处截面的速度云图和速度矢量图中可看出水流是自下而上流动,导致一些相对密度较小的砂粒在沉降过程中被水流卷起和水流一起流出。
