改进量子神经网络高压断路器故障诊断方法研究

张 莲，王 磊，禹红良，左兴喜，杨森淋

(重庆理工大学 电气与电子工程学院， 重庆 400054)

高压断路器是电力系统中重要的设备之一，广泛安装在电网中的各个部分，用于发电、输电、配电，以控制和保护电力设备。高压断路器故障诊断的研究有益于电力系统的安全稳定运行。可以及时发现并排除故障，对增强高压断路器的工作安全性、提高使用寿命、降低维护成本、避免电网重大事故发生有重要作用。根据对高压断路器长期运行统计，其中机械故障占全部故障的70%～80%，因此，高压断路器故障诊断主要研究其机械故障[1]。随着对高压断路器机械故障研究的深入，已经产生了多种诊断方法，如模糊理论、专家系统、支持向量机、BP神经网络等[2-3]。目前普遍采用的是BP神经网络算法，但由于BP神经网络本身具有的缺陷，在故障诊断时会有收敛速度慢、易陷入局部极小值等问题。而量子神经网络泛化能力、收敛速度快、分类能力较强、不存在陷入局部极小值的问题，是一种较好的故障诊断方法。

本文在量子神经网络的基础上，用量子进化对量子神经网络做出改进，建立改进的量子神经网络(improved quantum neural network, IQNN)高压断路器故障诊断模型，并用Matlab软件进行仿真，仿真表明该方法较BP网络具有更好的性能。

1 量子比特和量子门

1995年，美国Kak博士发表的一篇名为“On Quantum Neural Computing”的论文中[4]，首次提出量子神经计算，确定神经网络和量子计算两种方法可以结合，形成一种新的计算方法，为量子神经网络的发展奠定了基础。量子神经网络具有量子计算的一些特性，如：并行性、态叠加性和态纠缠性等，能使经典神经网络并行处理能力规模更大，效率更高[5]。

1.1 量子比特

传统计算的比特用“0”和“1”表示，相应地，在量子计算中量子比特用|0〉、|1〉表示，记号“| 〉”称为Dirac记号，用以描述量子线路的状态[6-7]。量子比特的状态不仅包括|0〉、|1〉，还包括这两种状态的线性组合，称为叠加态，即

|φ〉=α|0〉+β|1〉

(1)

其中α和β是一对复数，称为量子态的概率幅，即量子态|φ〉是以概率|α|2坍缩到|0〉，或者以概率|β|2坍缩到|1〉，且

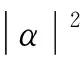
(2)

因此，量子态也可以用概率幅表示：|φ〉=[α,β]T。

1.2 受控量子旋转门

量子门是量子计算的基础。通过执行量子位状态的酉变换，可以实现逻辑功能[8]。

1.2.1 量子旋转门

量子旋转门的定义为

(3)

若 |φ〉=[cosφ,sinφ]T，那么经过变换U(θ) |φ〉=[cos(θ+φ),sin(θ+φ)]T。这里U(θ)起到相位变换的作用，故称为量子旋转门。

1.2.2 受控量子旋转门

该门有2个输入比特，分别为控制比特和目标比特。若控制比特置0，则目标比特保持不变；若控制比特置1，则目标比特相位旋转[9]。因此，受控旋转门描述为:

(4)

其受控参数k取值可分为以下情况：

1) 当k=1时，使|φ〉的相位发生θ角旋转，即C(k,θ)=[cos(θ+φ),sin(θ+φ)]T。

2) 当k=0时，此时|φ〉的相位保持不变。即C(k,θ)=[cos(θ+φ),sin(θ+φ)]T。

3) 当0

2 量子神经网络

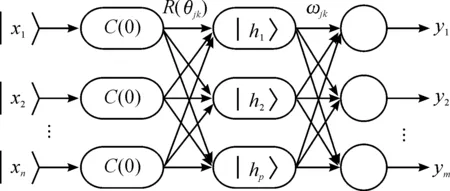
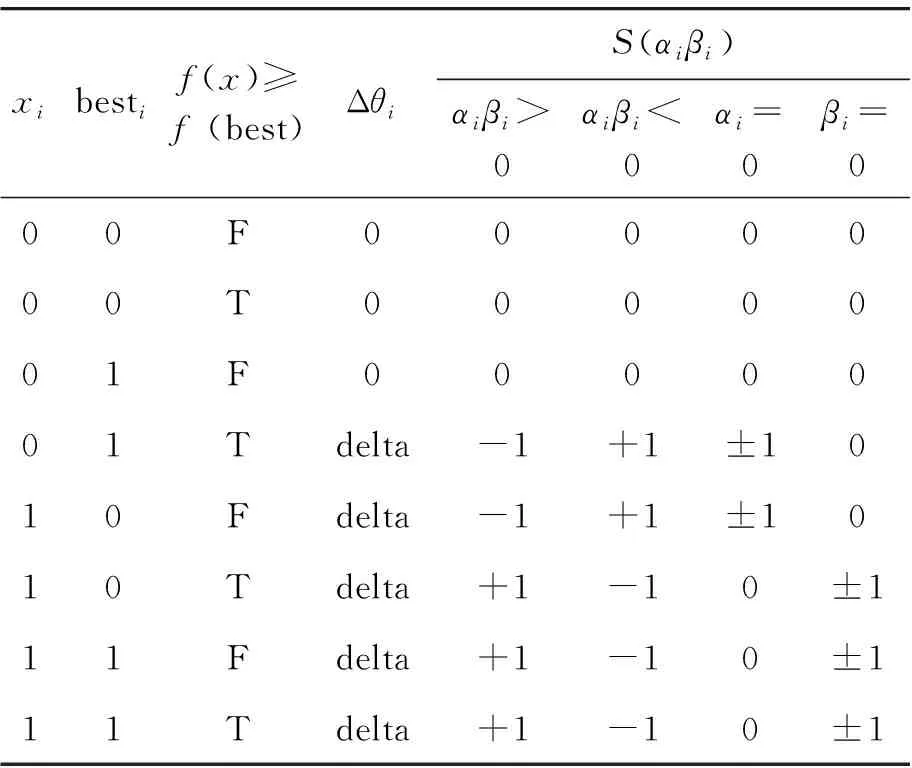
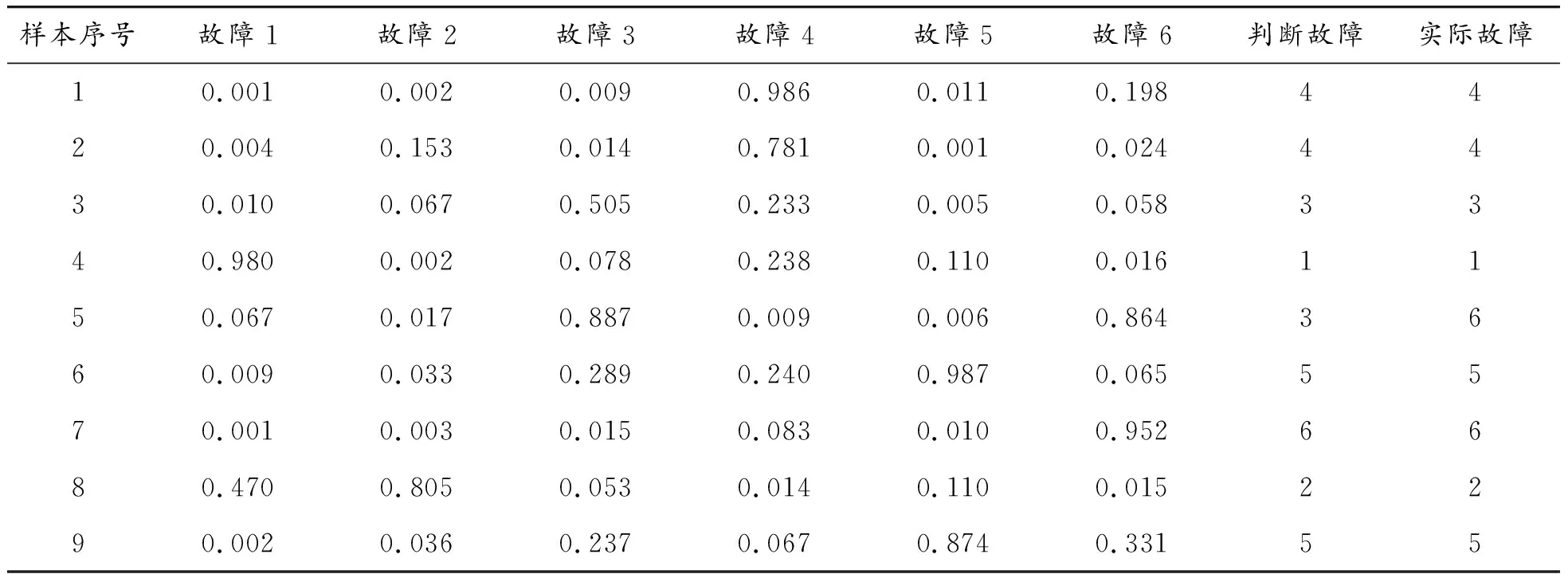
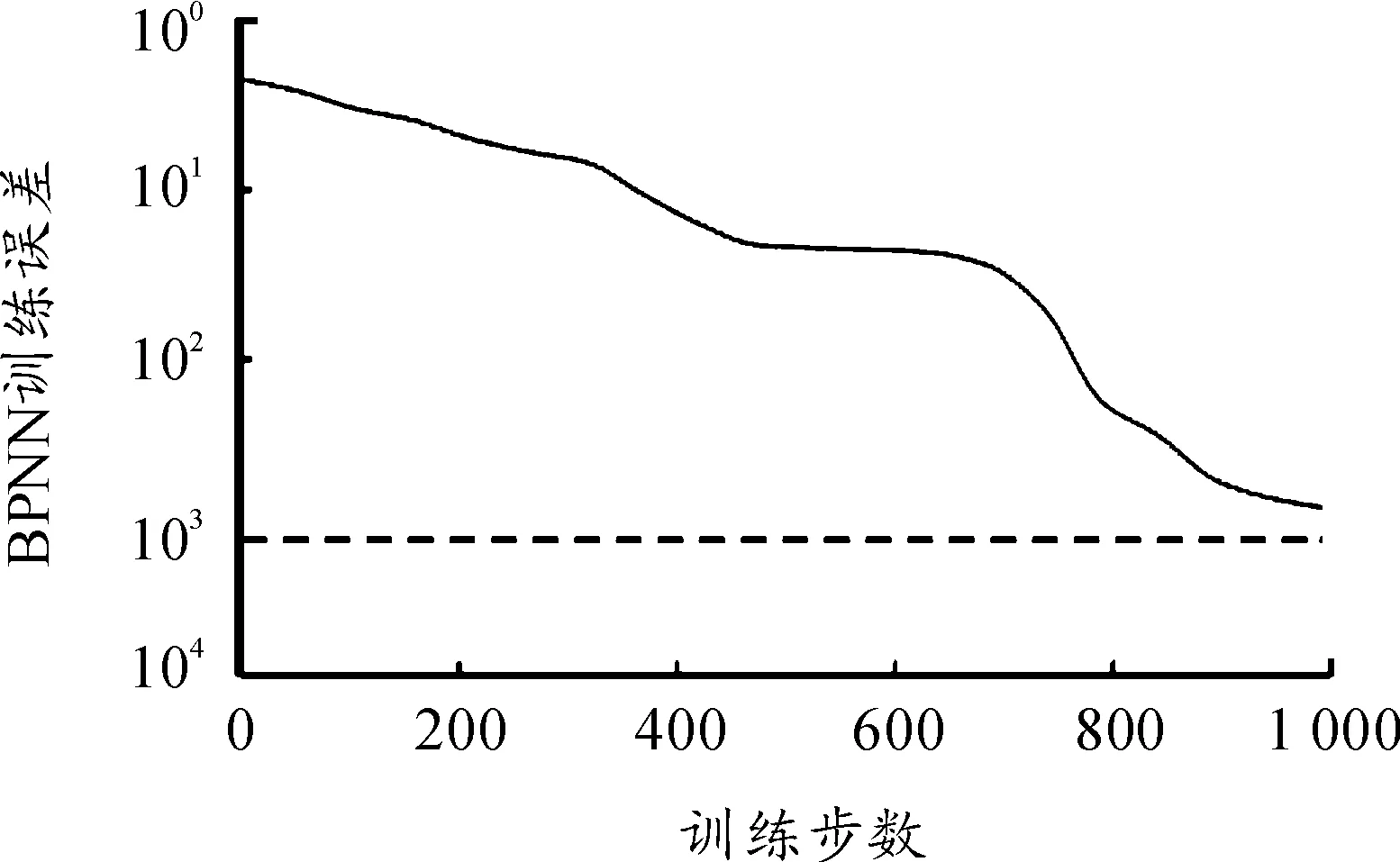
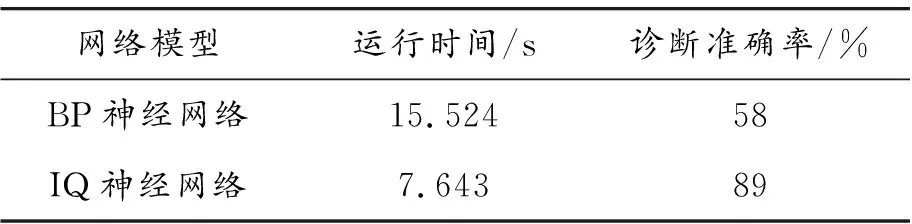
2.1 量子神经元

传统的神经网络神经元由两级激励函数(如常用的sigmoid函数)组成，借用量子理论中的量子旋转门，构建旋转门和受控旋转门的量子神经元模型[10]。其输入和输出用量子比特表示。移相、旋转分别用量子旋转门U(θi)和受控旋转门S(λ,φ)实现，其中S(λ,φ)的定义为：

S(λ,φ)=C(f(λ),φ)

(5)

其中:λ为受控参数;φ为相位变换大小;f(·)为sigmoid函数;函数C(·)和式(4)相同。量子神经元的模型如图1所示。

图1 量子神经元模型

|xi〉为输入样本的量子态描述，记输入样本向量为|X〉,则|X〉表示为：

|X〉=[|x1〉, |x2〉,…,|xn〉]T

(6)

其中|xi〉为

(7)

量子神经元的输出为

[cos(θ+f(λ)φ),sin(θ+f(λ)φ)]T

(8)

2.2 量子神经网络模型

本文提出的受控量子旋转门神经网络模型由3层组成，n个输入单元，p个隐层单元，m个输出单元。隐含层由若干个量子神经元组成。输出层为普通神经元，如图2所示。

图2 量子神经网络模型

|x1〉,|x2〉,…,|xn〉为输入序列，|h1〉，|h2〉,…,|hp〉为隐含层输出，wjk为输出层连接权，y1,y2,…,ym为网络输出，输出层采用sigmoid函数作为激励函数。

2.3 改进的量子神经网络参数调整步骤

运用量子进化理论确定量子旋转门的旋转角度的方法如表1所示。表1中f(x)为代价函数旋转角θi的取值：

θi=S(αi,βi)Δθi

表中Δθi和S(αi,βi)表示旋转角的步长和旋转方向。参数delta的取值与算法收敛度有关。采用动态量子旋转门的思想，delta的取值用式(10)确定：

(10)

其中：n为迭代步数，MAXGEN为终止代数；k为[0,1]之间的常数。

(11)

代价函数越小，其模型的拟合度越好。

改进的量子神经网络参数调整步骤如下：

3) 评估观测态P(x)的适应度。

4) 将最佳个体保留，并判断迭代步数是否达到最大步数，若达到，则转至步骤 8)，否则，执行下一步。

5) 根据式(9)计算量子旋转门的旋转角，并用式(10)中的量子旋转门作用于种群中所有个体的概率幅并更新Q(t)。

6) 执行量子交叉操作。把种群中的所有个体随机排序；然后对排序后所有个体循环移位，即第i位循环移位i-1次，获得交叉操作之后的新种群。

7)进化代数加1，进行量子变异，生成Q(t+1)，判断进化代数是否未达到最大迭代次数，若不满足则转至步骤2)，否则转至步骤8)。

8) 用梯度下降法继续训练网络，精确调整神经网络的权值和阈值，直到满足训练精度。

3 基于量子神经网络的高压断路器故障诊断模型

3.1 特征信号的提取

不同的特征信号反映高压断路器不同的故障信息，故特征信号的选择直接影响故障诊断的准确性。高压断路器的分合闸线圈是用来驱动断路器分合闸的，直接反映断路器的动作状态，加之流经分合闸线圈的电流是直流电，所以一般选择分合闸线圈电流为特征信号之一。分合闸线圈电流波形中包含了许多信息，其操作时分闸线圈电流波形图如图3所示。

图3 分闸线圈波形

根据铁芯的运动过程，分闸线圈电流一般分为5个阶段[11]：t0～t1阶段，铁芯保持静止，电流从t0呈指数增长；t1～t2阶段，铁芯开始加速，电磁力做功，线圈电流减小；t2～t3阶段，在t2时刻，铁芯停止运动，线圈电流又呈指数增大，该阶段是传动系统的带动下分断和闭合断路器触点的过程；t3～t4阶段，电流接近稳态；t4～t5阶段，电流断开，但辅助开关的触头间会产生电弧，电流下降，直至电弧熄灭。

(12)

对断路器的温度T进行检测以确定是否存在不良接触。测量线圈两端的电压可以反映电磁铁和操作回路的工作状态。因此，本文将提取断路器的分合闸线圈电流有效值、电流时间、线圈两端的电压、动触头的平均速度、控制箱内的温度等5个特征作为模型的输入向量。

3.2 故障诊断的步骤

基于改进量子神经网络对断路器故障诊断主要分为训练和诊断2个阶段，其主要步骤如下:

1) 将样本归一化，量子描述后形成训练样本集和测试样本集，输入故障诊断模型。

2) 设置相应的参数，用量子进化算法对网络进行训练，得到故障诊断模型。

3) 利用得到的故障诊断模型，对待测试的样本进行诊断。

4) 得到诊断结果。

3.3 高压断路器故障诊断模型的输入和输出

本模型的特征输入信号的选取如表2所示。

表2 特征信号

将特征输入量对应的故障类型作为诊断模型的输出量，选取的输出量为机构正常、操作电源故障、合闸铁芯开始阶段有卡涩、分合闸线圈短路、铁芯空行程过大和辅助开关动作接触不良等，对应的输出编码分别为(100000)(010000)(001000)(000100)(000010)和(000001)，如表3所示。

表3 故障类型

4 实验仿真与分析

本文选取34组故障数据，随机抽取25组作为模型的训练学习样本，剩余的9组作为测试样本。选择的特征向量长度为5，因此对应的输入神经元个数n为5。有6种故障状态输出，所以对应的输出神经元数m为6。经过多次实验对比IQNN的隐含层节点数p选择10。

经过训练样本对改进的量子神经网络训练之后，用测试集验证诊断模型的精度，得到的故障诊断结果如表4所示。

表4 实验结果和期望结果

从表4中可以看出：该诊断模型能对测试样本做出比较准确的判断。其中除了样本2、3、6外，判断故障的输出值都大于0.8，能很明确地判断出故障类型。样本3故障输出值中最大值为0.505，虽然相对于0.8比较小，但是该值远大于其他值，所以能判断故障类型为3号。对样本6的判断出现错误。

为了验证该模型的性能，同时采用原始的BP神经网络与之对比。采用这2种方法对同一样本集训练，得到的仿真结果如图4、5所示。图4为BPNN 训练误差曲线，图5为IQNN训练误差曲线。从图4中可以看出：BP神经网络的训练步数达到1 000步时，还没有达到所要求的误差精度。图5中IQNN的训练步数为300时，达到训练所要求的精度。可以看出：改进的量子神经网络在相同的训练精度下，训练步数大幅减少。

图4 BPNN训练误差曲线

图5 IQNN训练误差曲线

用BP神经网络和改进的量子神经网络对高压断路器进行故障诊断，得到两种模型的运行时间和诊断准确率的对照表，如表5所示。

表5 BP网络和IQNN诊断结果

从仿真实验结果可以看出：改进的量子神经网络高压断路器故障诊断模型在运行时间和诊断准确率上均优于传统的BP神经网络。

5 结束语

通过采用基于量子优化的量子神经网络对高压断路器进行故障诊断，利用分合闸线圈电流曲线和箱内温度等特征信号对模型训练后，可以准确判断出高压断路器操作机构的运行情况。仿真结果表明，改进的量子神经网络与目前传统的BP神经网络相比具有明显的优越性：训练步数短、故障诊断准确率高、很少陷入局部极小值，可以有效诊断高压断路器的机械故障。