三种二元变几何超声速进气道的调节方案设计及性能对比
2018-10-17谢旅荣
刘 雨,谢旅荣,汪 昆
(南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室, 南京 210016)
进气道是吸气式飞行器推进系统的重要组成部件,其作用是捕获、压缩自由来流,为燃烧室提供满足一定要求的气流。进气道高效高性能地工作是整个飞行系统高效运行的前提[1-3]。
对于宽工作马赫数范围的超声速进气道,必须保证在整个工作范围内正常工作。为满足低来流马赫数时进气道能正常起动,要求进气道的内收缩比较小,但是为了保证高马赫数时进气道的性能较好,则要求进气道的内收缩比要大,以减小总压损失[4],由此可见定几何的进气道型面难以同时兼顾高低马赫数下的性能,这种矛盾随着飞行器工作马赫数范围的增大而显得愈发严重。
目前常在进气道内外部流道处采取诸如抽吸、溢流等手段来降低自起动马赫数[5-8],但是这些流场控制措施改善效果有限,仍较难满足宽马赫数工作范围内进气道保持较高工作性能的要求。变几何进气道凭借其宽马赫数范围内的高性能优势受到国内外相关科研人员的重视[9-11],尽管它存在结构复杂、质量增加等缺点。
针对二元超声速进气道,以不同准则出发获得不同的压缩楔面调节规律是一种普遍采用的方案。美国Maryland大学研究的变几何进气道以不同来流马赫数时激波保持封口为目标,在提高流量系数的同时增加了升力[12];日本的空间航空研究院(ISAS)在20世纪80年代就实施了Air-Turbo Ramjet Engine(ATREX)计划,其中ATREX二元进气道则是通过转动楔面来调节激波系,提高进气道的捕获流量和压缩效率,以满足发动机的要求,这种调节迅速、简单且容易实现[13]。
国内对于变几何进气道也开展了相关研究。针对二元高超进气道宽马赫数大攻角工作要求,南京航空航天大学金志光等[14]研究了一种转动唇口变几何进气道调节方案,设计马赫数6.0的原型进气道不需要附面层抽吸装置即可在唇口开启过程中实现接力点起动,且自起动马赫数降至Ma=3.5;赵昊等[15]研究了一种第2级压缩面可调的变几何二元超声速进气道方案,通过旋转进气道第2级压缩面改变进气道前体激波的角度和位置,发现不仅可以提高进气道的流量系数,还可显著改善进气道的气动性能;袁化成等[16]提出一种内收缩比可控的变几何进气道方案,根据不同来流马赫数下外压段激波角度的变化,前后移动唇口,使得激波封口。
由上述的研究文献发现,其主要研究均是针对某一类变几何方案开展的,而对于不同方案的气动性能对比研究则较少。本文针对一个宽马赫数范围工作的三波系二元超声速进气道,设计了1种定几何进气道和3种变几何调节进气道方案,通过二维数值仿真研究对其流场特征和气动性能进行了分析、对比。其研究成果可以为超声速变几何进气道设计及方案选择提供参考依据。
1 进气道设计
1.1 定几何进气道设计
设计了如图1所示的工作马赫数范围为2.0~4.0的定几何进气道,型面设计时为提高工作马赫数范围内的流量系数,采用了非传统激波封口设计,即设计状态Ma=3.4时两道外压激波并不相交于唇口,而是保证Ma=2.4时第2道斜激波封口,Ma=3.4时第1道斜激波封口。该进气道第1级楔面压缩角(δ1)为7.0°。第2级楔面(δ2)压缩角为12.0°。进气道扩压段中心线采用前缓后急的变化规律,为获得较均匀的出口气流,在扩张段出口处有段等直段。考虑到结构强度和热防护问题,楔面前缘及唇罩前缘进行了钝化,钝化半径分别为0.3 mm和0.2 mm。
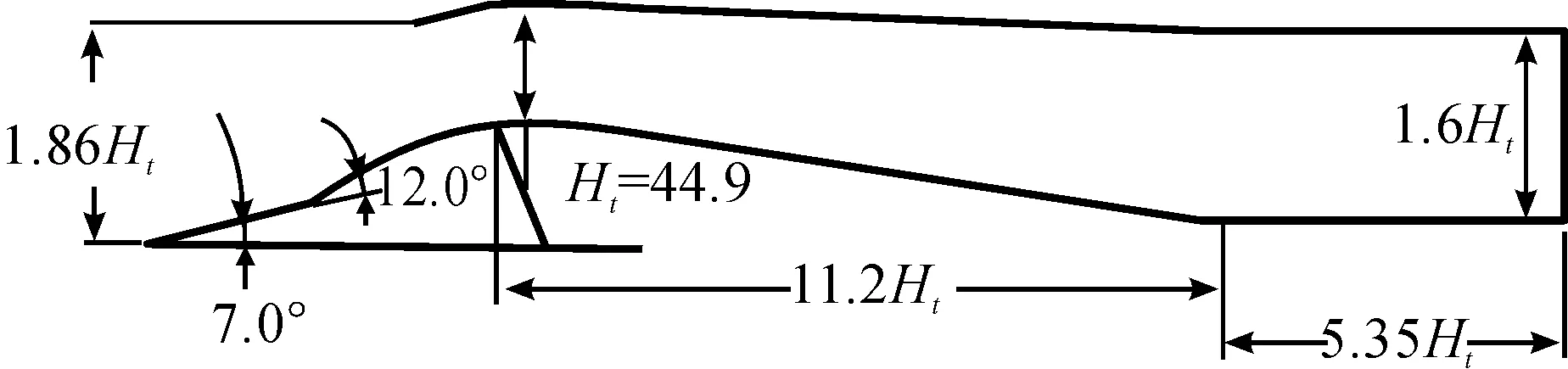
图1 定几何进气道几何型面示意图
1.2 变几何进气道型面设计及调节规律
1.2.1 变几何进气道型面设计原则
为方便起见,分别将定几何进气道以及3种变几何进气道设计方案命名为Plan A、Plan B、Plan C、Plan D。设计中保证相同来流马赫数下3种变几何进气道的第2道斜激波后马赫数保持相同。图2(a)是变几何进气道调节结构,在前体上,1、2级压缩面交点以及扩张段内分别设置有3个旋转轴A、B、E。进气道型面可以绕旋转轴转动。Plan A进气道为定几何进气道;Plan B进气道的整个前体部分绕铰接点转轴A旋转,即仅调节第1级楔面压缩角;Plan C进气道的第2级压缩楔面绕铰接点转轴B旋转,即仅调节第2级楔面压缩角;Plan D进气道的前体整体绕转轴A旋转,同时第2级压缩楔面绕转轴B旋转,即同时调节1、2级楔面压缩角。与此同时进气道内通道扩压段DE绕转轴E旋转,同步抬升D点与C点相平来保证喉道附近型面,实现进气道的喉道截面高度以及泄流腔宽度的调节。图2(b)~(d)分别是3种变几何进气道在来流马赫数为4.0时的型面调节示意图。
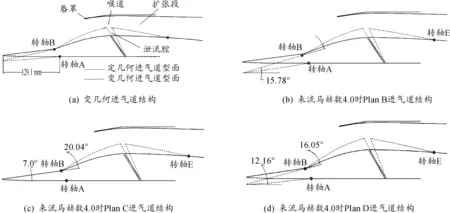
图2 变几何进气道
图3是泄流腔滑板机构的示意图,利用此机构便可保证泄流腔壁板在绕底端旋转的同时不断伸展。其中Plan B、Plan D方案增大了进气道的流量捕获面积,Plan C方案进气道捕获面积不变。

图3 泄流腔滑板结构
1.2.2 变几何进气道型面调节规律
在型面调节转动设计的过程中,为满足宽马赫数的工作范围,需要同时兼顾低马赫数的流量捕获、工作马赫数范围内较低的喉道马赫数和高马赫数前体激波不可打入内通道等,对于Plan B方案的变几何进气道,经过多轮设计初步确定了Ma为2.0、2.4、2.8、3.0、3.4、4.0这6个典型状态点的型面。随后通过多项式拟合得到了进气道的前体偏转角度α(°)随来流马赫数Ma的变化规律为:
α=23.75-28.6·Ma+
10.51·Ma2-1.074·Ma3
对于Plan C、Plan D方案的变几何进气道,在控制第2道斜激波后马赫数与Plan B方案相同的前提下,通过几何计算可以得到其相应的变几何楔面偏转规律。3种变几何方案均可以实现随着来流马赫数的增大,前体总压缩角逐渐增大,喉道面积随之变小,内收缩比逐渐增大。 图4给出了变几何进气道的结构示意图(δ3为唇罩压缩角,Ht为喉道高度)。图5给出了变几何进气道的楔面调节规律以及喉道高度变化规律。

图4 变几何进气道外压段结构示意图

图5 变几何进气道调节规律
2 仿真方法及验证
2.1 数值计算方法
本文采用Fluent软件进行数值模拟,湍流模型选择标准k-ε模型,近壁面采用标准壁面函数法处理,对近壁面网格进行了加密以便模拟边界层流动。计算域划分结构网格,网格数量12万左右。
本文所设计的进气道均用于亚燃冲压发动机,通过设置进气道出口反压来模拟燃烧室压力变化,并调节反压来改变进气道结尾激波位置,当结尾激波位于喉道附近时,认为进气道处于临界工作状态,即最佳工作状态。
计算过程中监控方程残差及进气道喉道马赫数与出口流量。当残差下降3个数量级且喉道马赫数与出口流量稳定时,认为计算收敛。
计算来流条件见表1。

表1 进气道来流参数
2.2 算例验证
为验证本文所采用的数值模拟方法的可信度,利用文献[18]中的进气道几何构型和实验数据进行了算例验证。实验来流条件:自由来流Ma=2.41,来流总压540 kPa,总温305 K,进气道隔离段长79.3 mm,出口为通流状态。
图6所示为仿真数据与实验结果的对比。由图6(a)可见本文采用的数值方法能清晰捕获进气道内的各种斜激波与反射激波,流场结构与实验结果基本吻合。图6(b)对比了仿真与实验测得的壁面压力分布,可见计算的壁面沿程压力分布与实验所测数据基本吻合,说明本文采用标准k-ε模型进行计算研究是可行的。
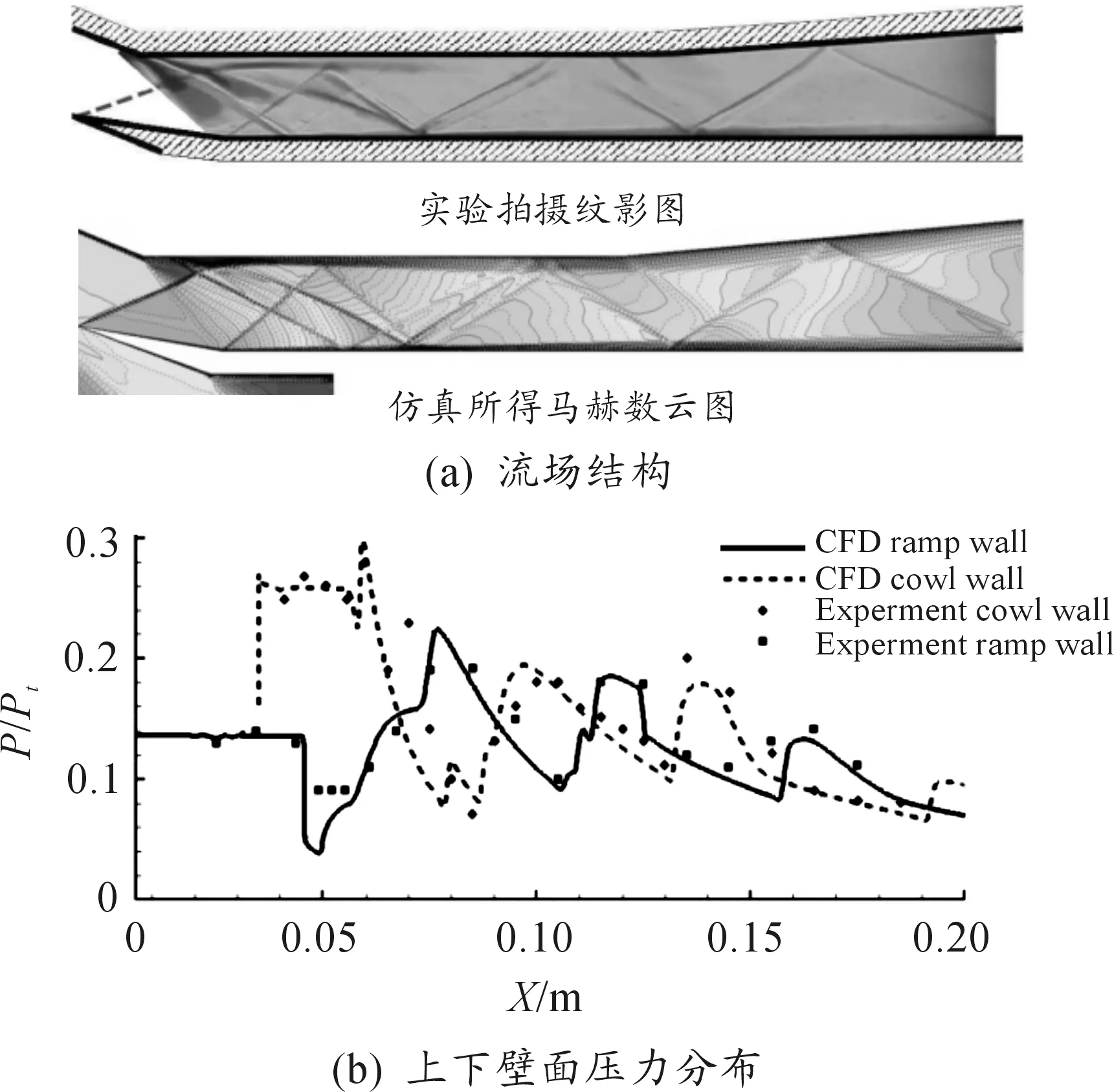
图6 实验与仿真结果对比
3 结果与分析
3.1 定几何进气道流场分析
对于定几何进气道,在整个飞行马赫数范围内其几何型面保持不变。图7给出了数值仿真所得的部分状态点流场马赫数云图。
由图7可以看出:随着来流马赫数的增大,激波角逐渐减小,同时在来流马赫数为2.4时,第2道斜激波封口,在来流马赫数为3.4时,第1道斜激波封口。此种设计的进气道相较于传统设计的激波相交封口进气道,虽然在高马赫数下总压恢复稍低,但是在宽马赫数范围内的流量系数较高[19]。但随着来流马赫数继续增大,激波进入唇罩内部,并且与唇罩内部上壁面附面层相交引起分离,这对于进气道内流场稳定性以及进气道抗反压能力都不利[20]。
3.2 Plan B变几何进气道流场分析
当飞行器加速至马赫数2.0以上时,进气道型面开始按所设计的规律进行调节。随着飞行马赫数的不断增大,进气道的整个外压缩面绕A点旋转。此时第1级楔面角度增大,对来流的压缩强度不断增大,第2级楔面对来流的压缩角保持不变,喉道面积减小,内收缩比增大。图8给出了Ma∞=2.0~4.0变化时Plan B方案的几个典型状态点的进气道流场马赫数云图。
从马赫数云图可以看出:对于Plan B方案的变几何进气道,从马赫数2.4开始,第2道斜激波一直保持封口状态,并且在马赫数增大至3.0之后,第1、2道斜激波始终保持相交于进气道唇口。既保证了较大的流量系数,同时避免了斜激波进入唇口内与进气道上壁面附面层产生干涉引起的分离。

图7 定几何进气道马赫数云图(Ma∞=2.0~4.0)

图8 Plan B变几何进气道马赫数云图(Ma∞=2.0~4.0)
3.3 Plan C变几何进气道流场分析
按照本文设计的调节规律,随着飞行马赫数的不断增大,进气道的第2级压缩楔面绕B点(即1、2级压缩楔面交点)旋转。此时第1级楔面对来流的压缩角保持不变,第2级楔面压缩角不断增大,喉道面积减小,内收缩比增大。图9给出了Ma∞=2.0~4.0变化时Plan C方案在典型状态点的进气道流场马赫数云图。
可以看出Plan C变几何方案同样可以在来流马赫数2.4以上时保证第2道斜激波封口。但是由于第1级压缩面楔角不变,所以当来流马赫数达到3.4以上时,第1道斜激波与第2道斜激波在唇口前方提前相交,产生的滑流层进入内通道。随着来流马赫数的增大,两道激波相交引起的滑流层以及对进气道上壁面的干扰也越严重。
3.4 Plan D变几何进气道流场分析
按照本文设计的调节规律,随着飞行马赫数的不断增大,进气道的外压缩楔面整体绕A点旋转,同时第2级压缩楔面绕B点(即1、2级压缩楔面交点)旋转。此时1、2级楔面压缩角都以一定规律增大,喉道面积减小,内收缩比增大。图10给出了Ma∞=2.0~4.0变化时Plan D方案的几个典型状态点的进气道流场马赫数云图。
可以看出Plan D变几何方案在来流马赫数2.8以上时第2道斜激波封口,在来流马赫数3.0以上时1、2道激波相交封口。但是对比Plan B方案,由于第2道楔板也进行调节,所以喉道截面的调节幅度更大,故喉道马赫数更小,有利于提高进气道高马赫数下的总压恢复系数。

图9 Plan C变几何进气道马赫数云图(Ma∞=2.0~4.0)

图10 Plan D变几何进气道马赫数云图(Ma∞=2.0~4.0)
3.5 定/变几何进气道气动性能比较
图11给出了定/变几何进气道喉道马赫数随来流马赫数变化曲线。可以看出在整个工作范围内,3种变几何进气道的喉道马赫数均低于定几何进气道。结合上面的流场图可以看出,3种变几何进气道均不同程度地增加了进气道外压缩面的总压缩角,提升了进气道的外压缩能力。同时喉道面积的减小、内收缩比增大,使得内压缩能力提高,从而使得变几何方案在整个工作范围内都能获得低于定几何进气道的喉道马赫数。
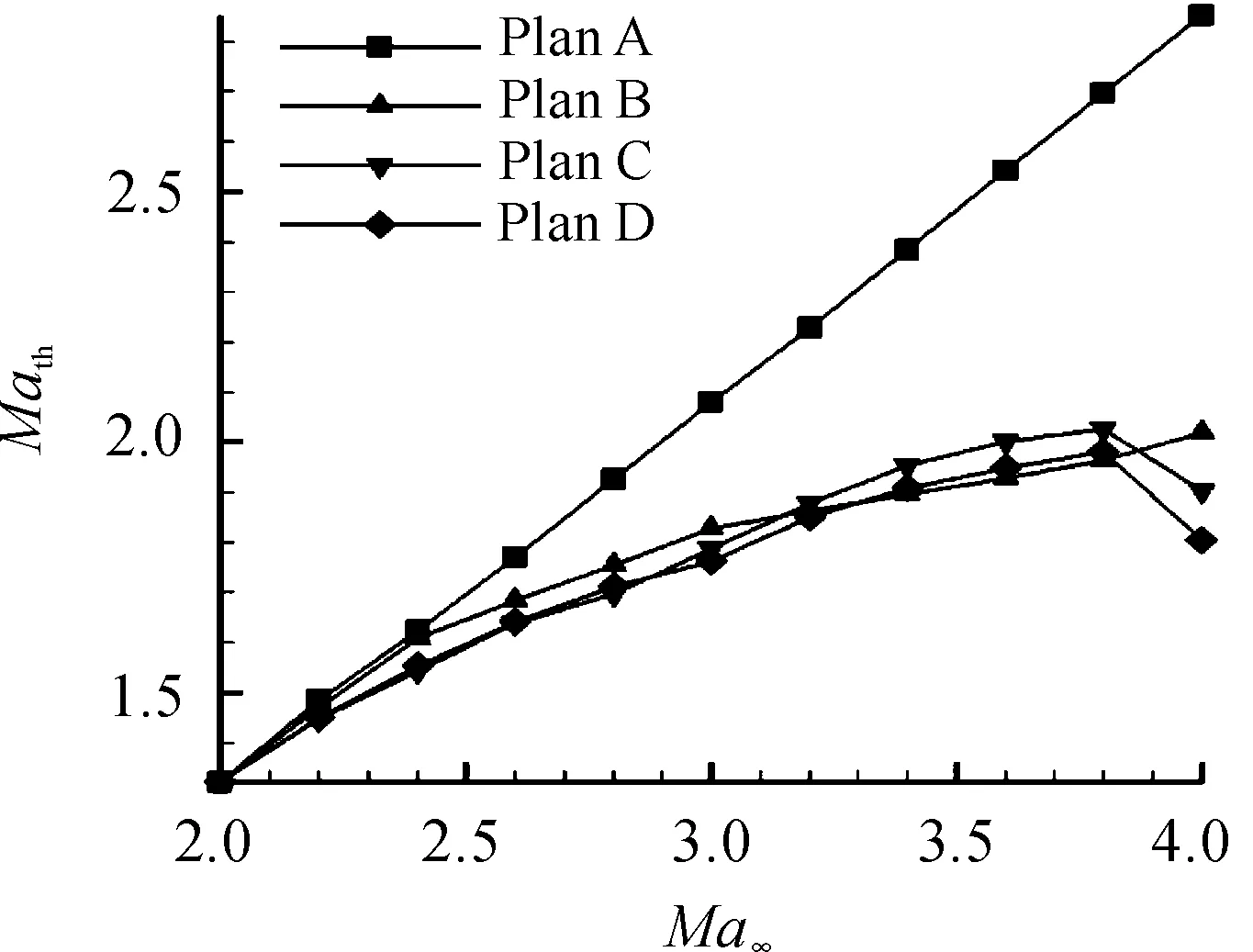
图11 定/变几何进气道喉道马赫数随来流马赫数变化曲线
图12给出的是4种定/变几何进气道流量系数随来流马赫数变化曲线。可以看到C方案在马赫数2.8以下时流量系数稍小于Plan A定几何进气道,在马赫数2.8以上时与A方案近乎相同。B和D方案的流量系数较Plan A定几何方案要小一些。但是由于B、D方案增大了进气道的流量捕获面积,因此进入进气道的绝对流量大于定几何方案。由图13可见,相较于A方案,Plan B和Plan D方案最多可增加22.3%和11%的流量。
图14给出的是定/变几何进气道临界总压恢复系数随来流马赫数变化曲线。定/变几何进气道的临界状态总压恢复系数随来流马赫数升高都持续降低,这是因为来流马赫数增大,进气道外压段斜激波系与内压段激波串的损失都会增大。由于3种变几何方案都随来流马赫数升高而增大了外压缩段对气流的压缩角,并且增大了内收缩比,因而喉道马赫数较定几何进气道更低,总压损失更小,总压恢复系数更高。当来流马赫数为4.0时,D方案的总压恢复系数较A方案提高了50%。

图12 定/变几何进气道流量系数随来流马赫数变化曲线
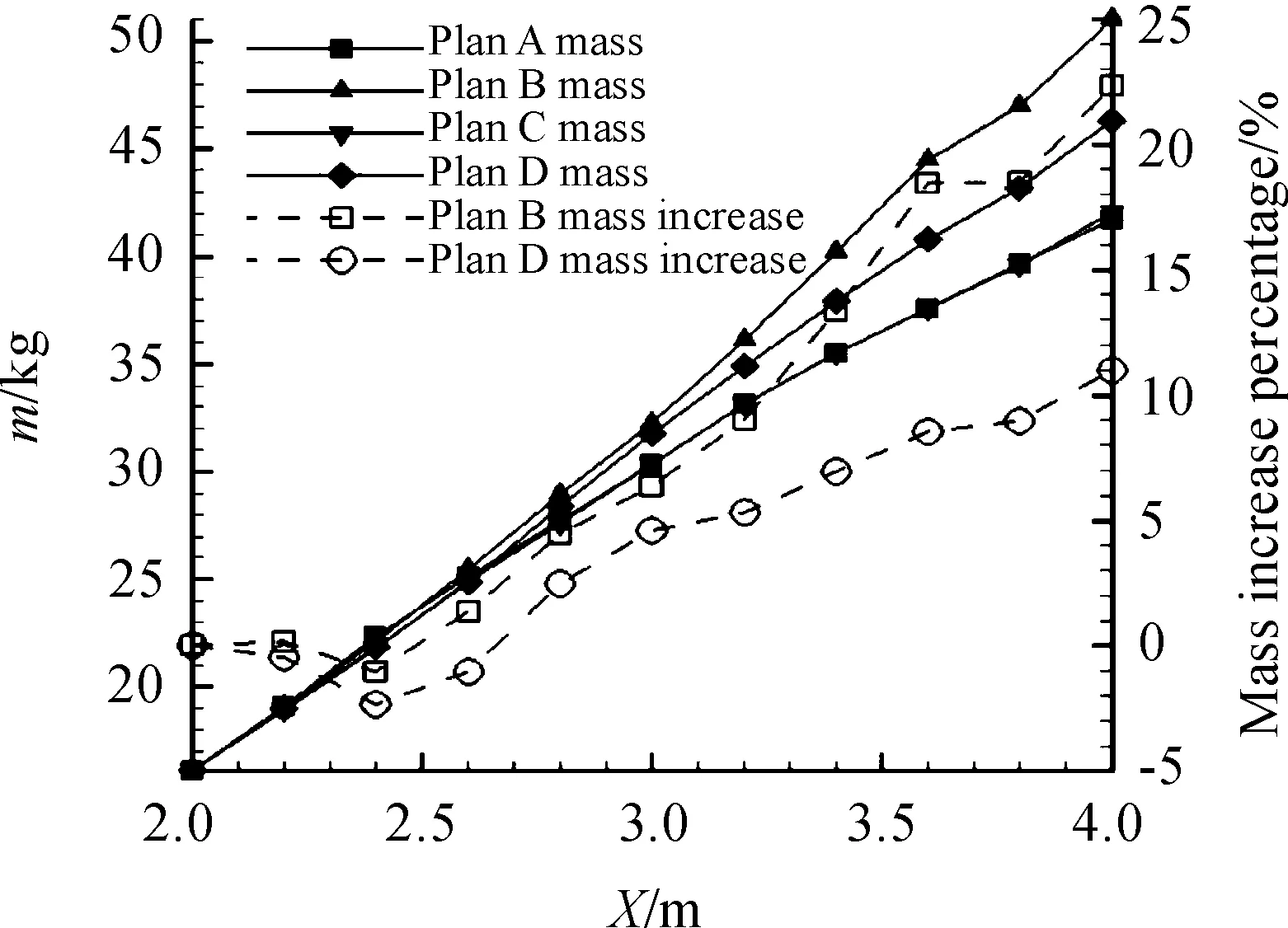
图13 定/变几何进气道捕获流量随来流马赫数变化曲线
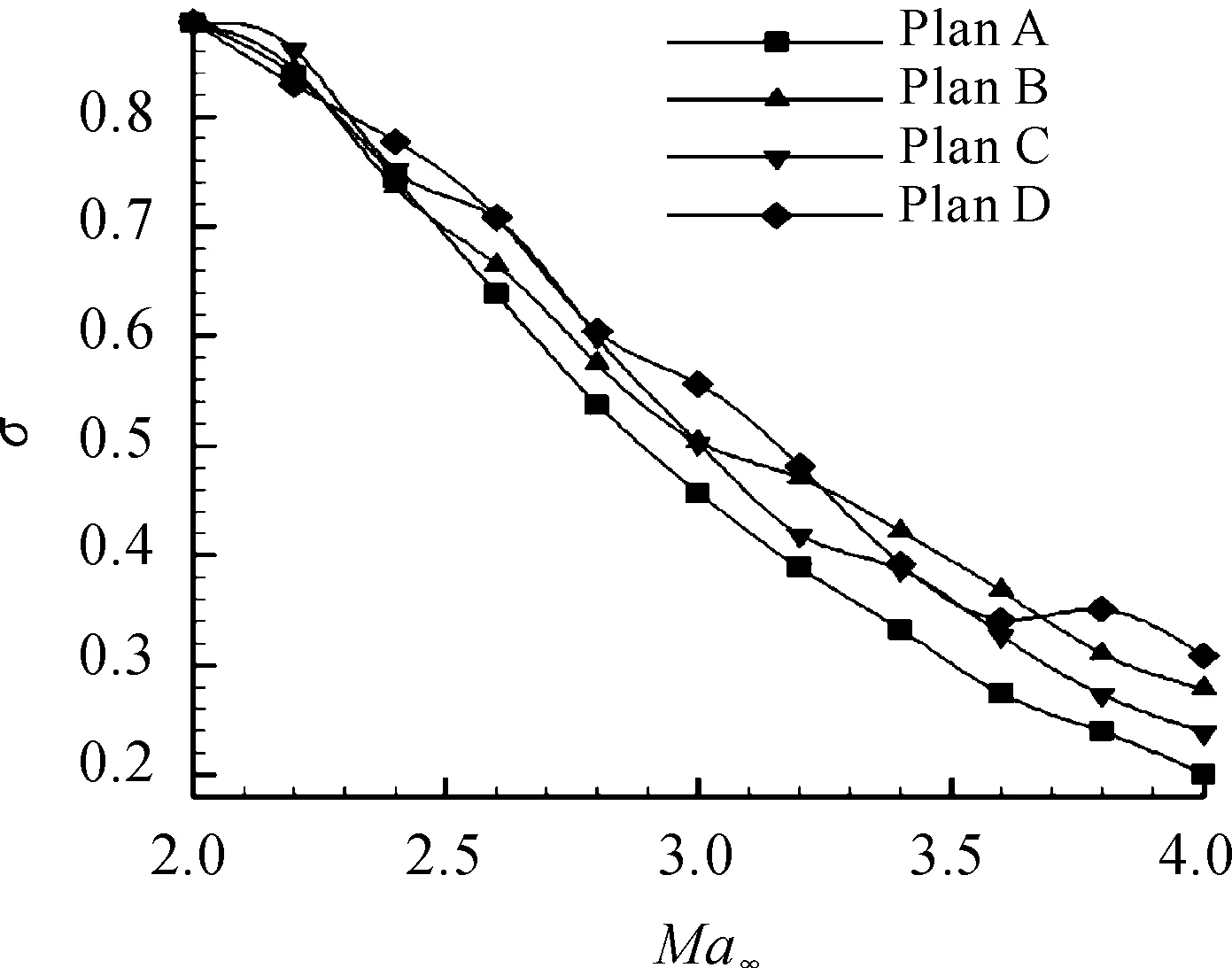
图14 定/变几何进气道临界总压恢复系数随来流马赫数变化曲线
图15是4种定/变几何进气道的阻力系数随来流马赫数变化曲线,可见在整个工作范围内四种进气道的阻力系数都随来流马赫数增大呈先下降后上升的趋势。定几何进气道在来流马赫数Ma<2.8以及Ma>3.6时其阻力系数明显小于3种变几何进气道。这意味着变几何进气道的捕获流量增大和总压恢复系数升高是以阻力系数增大为代价的。

图15 定/变几何进气道阻力系数随来流马赫数变化曲线
由于发动机的净推力与流量、总压恢复系数成正比,与进气道外阻力成反比。因此可以定义一个进气道性能综合指数s:
s=σ·Q/Cs
其中σ、Q、Cs分别为进气道的总压恢复系数、进气道流量、进气道阻力系数。
图16给出了定/变几何进气道性能综合指数随来流马赫数变化曲线。可以看到在低马赫数时(Ma<2.6),3种变几何进气道的综合指数略低于定几何进气道;当来流马赫数在2.6以上时,3种变几何进气道的综合指数均大于定几何进气道,且Plan B、Plan D方案较Plan C更优。
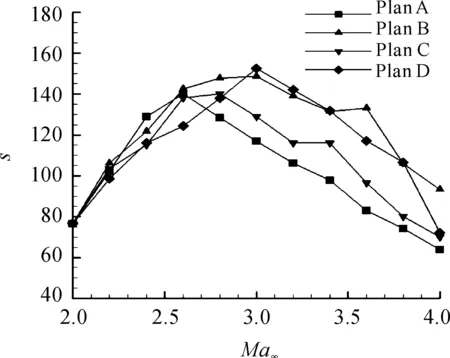
图16 定/变几何进气道性能综合指数随来流马赫数变化曲线
图17给出的是定/变几何进气道临界压比(临界状态进气道出口静压/远前方来流静压)随来流马赫数变化曲线。可以看出随着来流马赫数的增大,进气道所能承受的最大反压也升高。相同来流马赫数下,变几何B、C、D方案的抗反压能力较定几何方案更强,且来流马赫数越高,定/变几何进气道的抗反压能力差别越大。
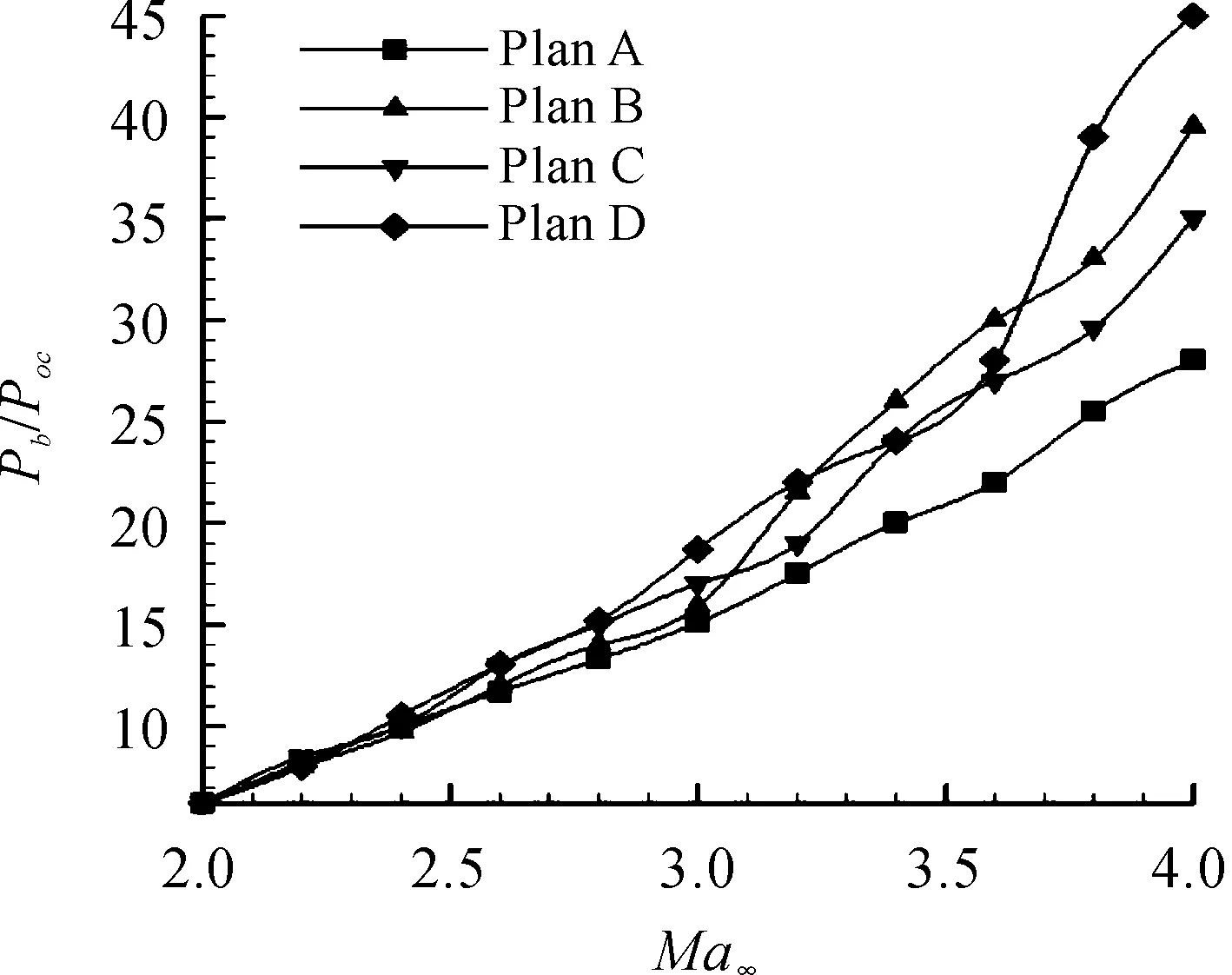
图17 定/变几何进气道临界压比随来流马赫数变化曲线
4 结论
针对一个工作在Ma∞=2.0~4.0的三波系二元超声速进气道,设计了1种定几何进气道和3种变几何楔面调节方案,对这4种进气道开展了数值仿真研究,结果表明:
1) 仅调节第1级楔面压缩角和1、2级楔面压缩角同时调节的变几何进气道捕获的流量均高于定几何进气道,仅调节第2级楔面压缩角的变几何进气道流量在低马赫数(2.8以下)时略低于定几何进气道,在高马赫数时与定几何进气道近乎相同;
2) 在研究范围内,3种变几何进气道的临界总压恢复系数均高于定几何进气道。与定几何进气道比较,仅调节第1级楔面压缩角的变几何进气道的临界总压恢复系数最高可提高38.6%,1、2级楔面压缩角同时调节的变几何进气道的临界总压恢复系数最高可提升53.7%;
3) 本文所设计的变几何进气道在宽马赫数范围内提高了进气道气动性能,综合考虑,仅调节第1级楔面压缩角的变几何进气道和1、2级楔面压缩角同时调节的变几何进气道较仅调节第2级楔面压缩角的变几何进气道性能更优。
