轮胎侧偏非稳态特性测量方法研究

李 飞，姜清伟，李 洋

(中国汽车技术研究中心有限公司， 天津 300300)

轮胎是汽车与地面直接相互接触的部分，其动力学特性将很大程度上影响车辆的运动姿态。轮胎的侧偏特性主要影响着汽车的操作稳定性和行驶安全性等。车辆许多电控系统如ESP等作为实时控制系统，主要是对轮胎非稳态特性进行控制的研究。

20世纪50年代Eric Gough通过试验证明了轮胎侧偏过程中胎面的变形原理[1]。1991年Gim等在胎面刷子模型的基础上(carcass无弹性)假设印迹内负荷散布为简化的抛物线，推导出轮胎纯侧偏、纯纵滑、纯侧倾以及纵滑侧偏联合工况下的轮胎力学模型。Apetaur于1992年基于轮胎变形力与瞬时参数(侧偏角、纵向滑移率、路径曲率)对应的稳态力相平衡的假设，建立了轮胎瞬态响应时域微分方程的表达式[2]。Pacejka 和Higuchi在1997年将松弛长度引入到弦模型中用来表达动态特性，并结合Magic Formula半经验模型表达稳态特性，分析了轮胎侧倾工况及大侧向滑移率工况的非稳态力学特性[3]。Pacejka和Besselink在1997年将Magic Formula与松弛长度概念相结合，得到了形式简洁、用于表达低频输入下侧纵向轮胎力学特性的非稳态模型[4]，通过试验研究发现，一阶松弛系统能够准确地描述侧向力非稳态过程，但回正力矩的响应却不能仅由一阶松弛系统进行表达，因此Maurice 和Pacejka在1999年建立了适用轮胎侧向力学特性的非稳态模型，模型中用一阶松弛系统串联相位超前系统计算回正力臂，再由侧向力与回正力臂相乘得出回正力矩[5]。

从轮胎运动状况来分，轮胎力学特性可分成稳态与非稳态特性。当汽车在平稳路面上行驶，且汽车的行驶条件不发生突变时，汽车的横摆频率一般低于2 Hz，此时轮胎近似表现为稳态(准稳态)。然而事实上汽车不可能一直行驶在平稳状态，往往汽车在行驶过程中会遇到行驶状态的突然改变，例如急转向、紧急避障、紧急变道超车等，轮胎特性都会展现出典型的非稳态[6-9]。而侧向松弛长度则是表征轮胎侧向非稳态特性的一个关键参数，通过对该参数的精确测量，可实现对轮胎非稳态的特性的研究，建立精确的轮胎非稳态侧偏模型。

1 轮胎非稳态侧偏模型

只考虑轮胎侧向平移刚度，忽略胎宽及胎体的弯曲扭转刚度的影响，轮胎系统则为连续线性定常系统，忽略轮胎质量与陀螺效应，轮胎只做小幅运动整个印记区域内无相对滑动。

如图1所示，XOY为大地坐标系，xoy为轮胎接地印迹随动坐标系，c点为车轮中心，a为印记半长，ψ(X)为车轮转角，Y(X)为车轮侧向位移。根据假设胎面上点自进入接地印迹内至离开接地印迹内与地面不发生相对滑动，且刚进入时有：

Yt(X,0)=Yc(X,0)

(1)

印记内无侧向滑动有：

Yt(X,x)=Yt(X-x,0)

(2)

刷毛变形量Δy(X,x)为：

Δy(X,x)=Yt(X,x)-Yc(X,x)

(3)

依据几何关系有：

Yc(X,x)=Y(X)+(a-x)*

ψ(X)+yc0(X)

(4)

结合式(1)-(4)有：

Δy(X,x)=Y(X-x)-Y(X)+

yc0(X-x)-yc0(X)+

a[ψ(X-x)-ψ(X)]+xψ(X)

(5)

将变形在整个印记区间积分可得

(6)

进行拉氏变换后有：

(7)

写成传递函数形式：

(8)

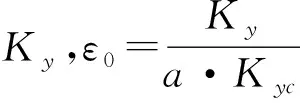
引入的E函数E(s)为：

(9)

将E函数泰勒级数展开并忽略高阶无穷小项进行1阶近似E(s)≈as可得：

(10)

(11)

依据准稳态概念可得：

(12)

其中Vsyn为轮心输入名义侧向滑移速度，Vsy为胎面与地面的有效侧向滑移速度。由此看出松弛效应的本质是轮心输入经过胎体弹性滞后以后引起胎面实际有效滑移速度的延迟。依据式(12)以及轮胎的稳态特性可将轮胎系统表示如图2所示。

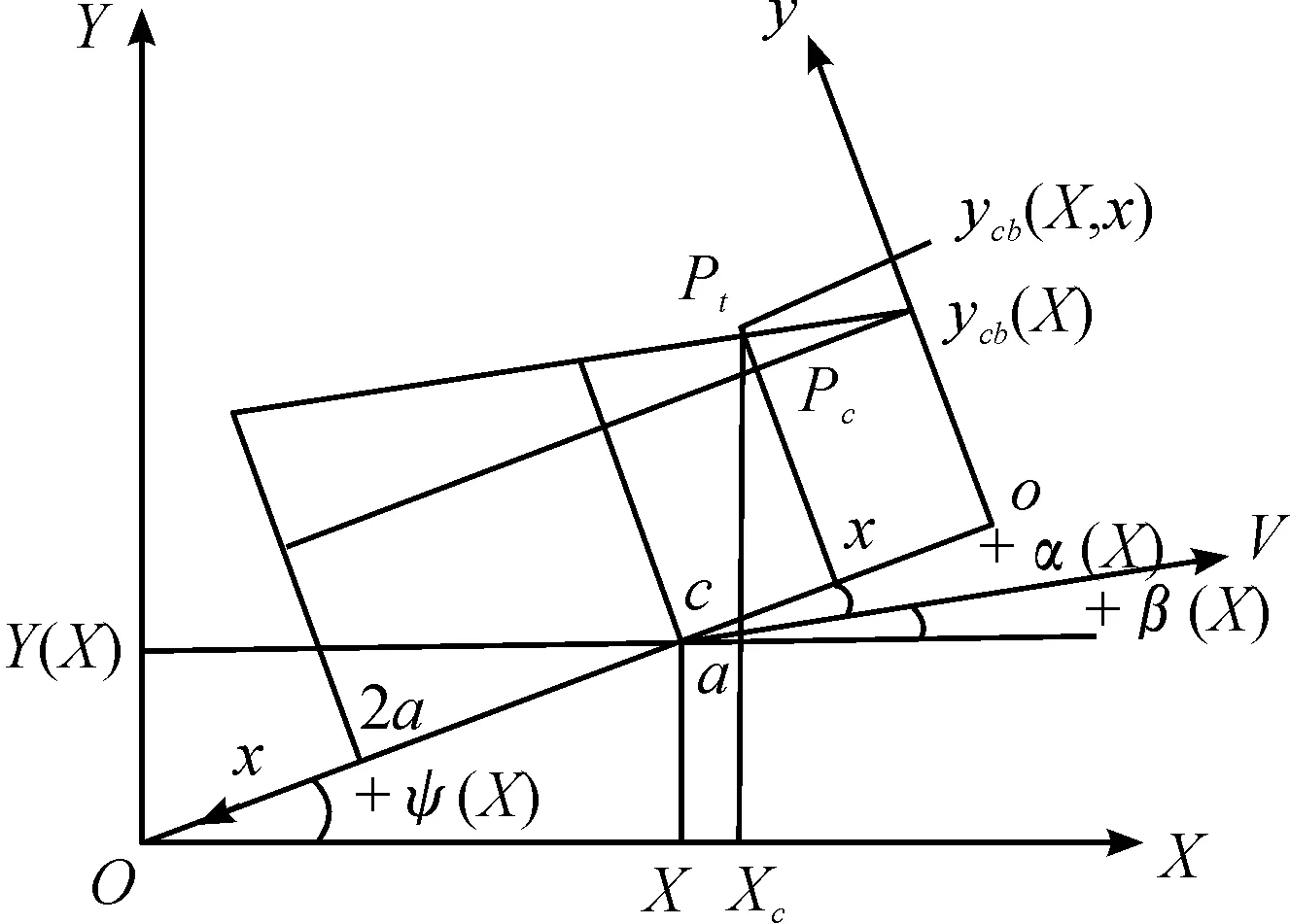
图1 地面接触印迹内胎体胎面变形

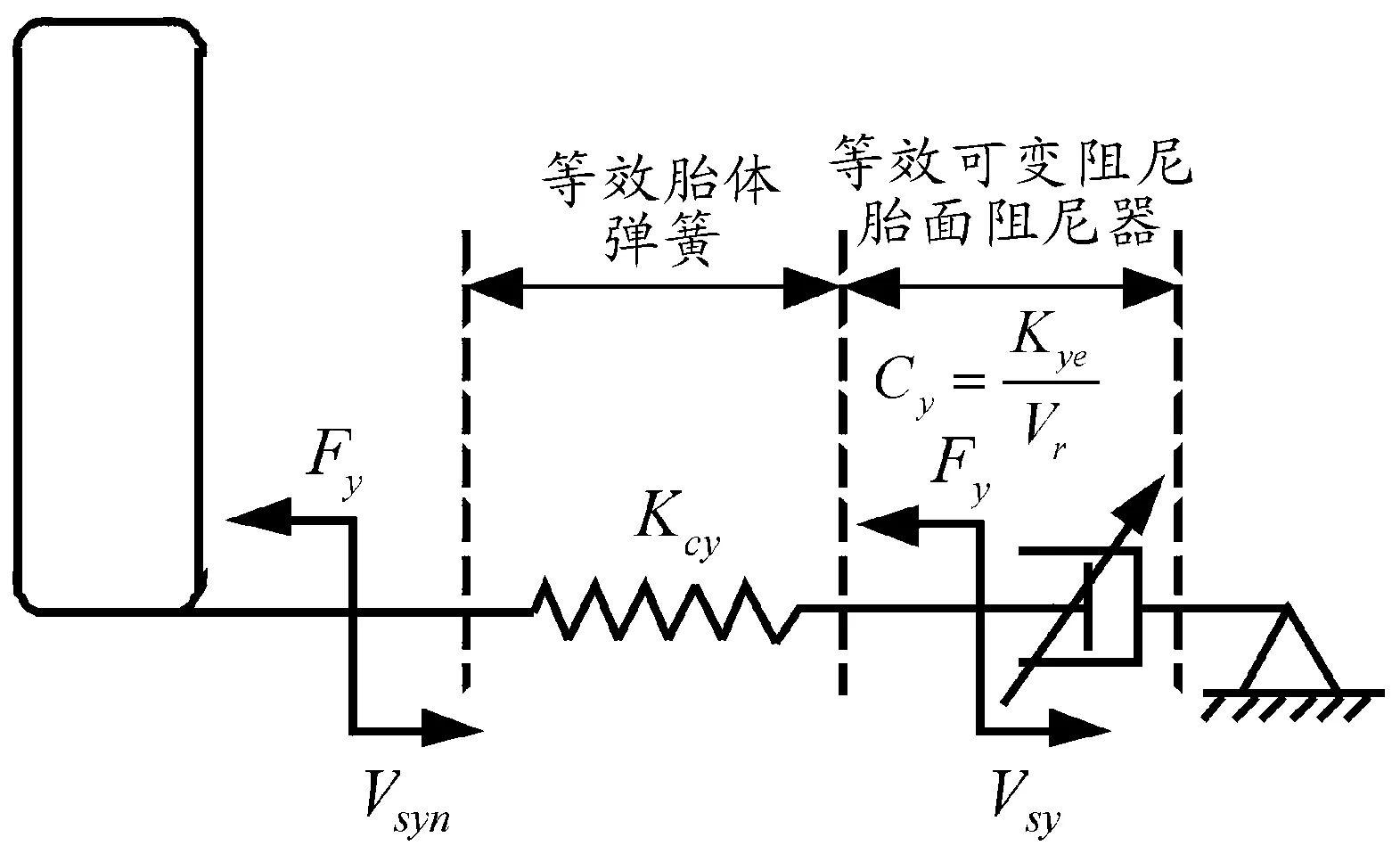
图2 简化后的轮胎与地面物理模型示意

图2中：Kcy表征胎体的侧向弹性；Cy表征胎面与地面相互作用的等效阻尼特性。由于无纵向滑移且输入为小侧偏角输入，将式(12)两边通除Vx有[11]：

(13)

式(13)可写为

(14)

其中Ky为侧偏刚度。拉氏变换后得输入为轮心侧偏角，输出为实际侧向力的传递函数G(s):

(15)

依据控制论理论[12]求得单位侧偏角阶跃输入下的侧向力在空间域的响应表达式：

(16)

由式(16)得当侧向力上升至稳态值的63.2%时所滚过的距离即为侧向松弛长度。

2 侧偏松弛长度测量方法设计

轮胎侧偏非稳态特性是描述轮胎从侧偏角施加开始到侧向力达到稳定的过程，试验测量方法中需要设计侧偏角的阶跃输入，来测量侧向力随轮胎滚动距离的关系。在实验台测试中，期望轮胎侧偏角和测试速度都能够同时阶跃地(无时间延迟)施加到轮胎上，但在实际操作中是不可能实现的，因此只能先在静止状态施加其中一个变量，再迅速施加另一个变量，这样就形成2种测试方法：先施加侧偏角再施加测试速度的侧偏角阶跃法和先施加测试速度再施加轮胎侧偏角的转动角阶跃法，且侧偏角阶跃法还具有2种测量方法，接下来将对每种测量方法进行逐一分析研究。

2.1 侧偏角阶跃法

轮胎的侧偏运动是轮胎在受到侧向力作用时引起的轮胎在向前滚动的同时具有侧向运动。因此理想的单位侧偏角阶跃输入过程应当如图3所示[1]。

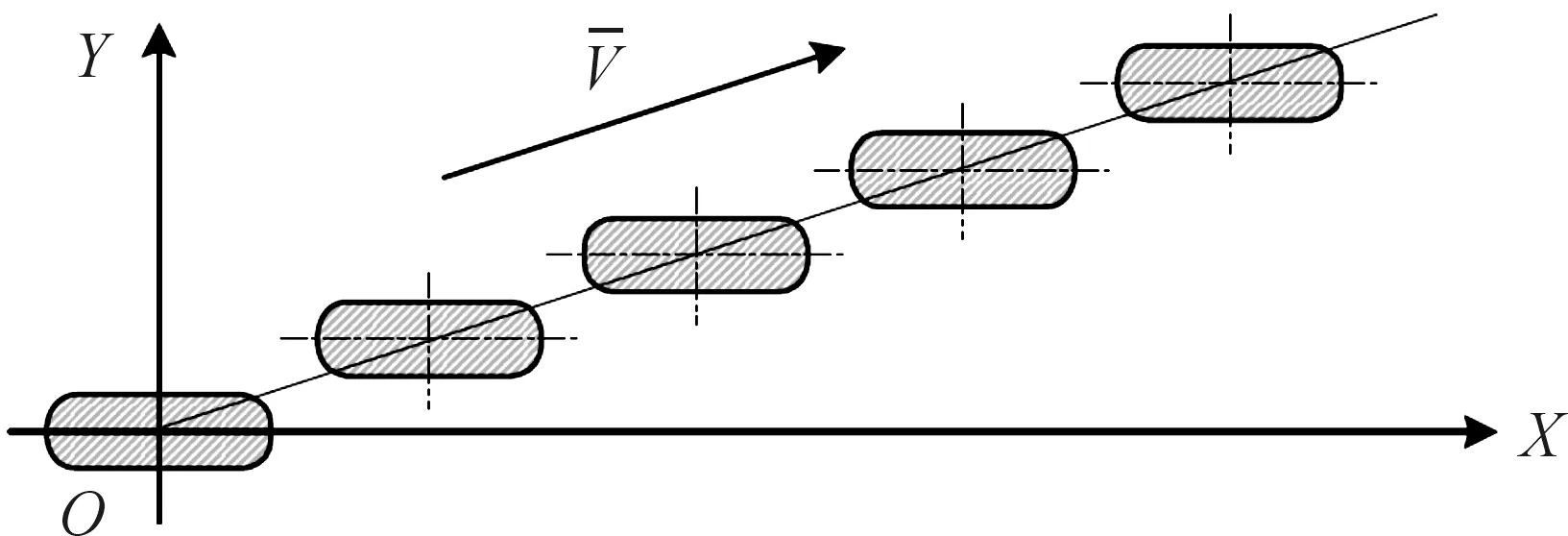
图3 轮胎侧偏角阶跃过程

轮胎延X轴滚动，自坐标原点O开始瞬间施加侧向阶跃运动，且轮胎的速度方向与X轴夹角为小侧偏角(通常采用1°侧偏角，确保在轮胎线性区特性里运动)，完成单位侧偏角阶跃过程。

通过调研和研究发现，侧偏角阶跃方法主要有2种测试方法：

1) 先转角后加载法。先将轮胎悬空(无载荷状态)施加1°转向角，然后加载到试验载荷。由于轮胎的侧向力响应过程只与滚动距离有关而与时间无关，此时可认为轮胎沿着轮胎中心平面方向自远处滚动至加载位置，即将轮胎中心平面方向当作大地坐标系中的X轴，加载位置即为坐标原点O。然后迅速启动钢带到指定速度，钢带运动方向即为轮胎的速度方向，速度方向相对于大地坐标系X轴夹角为1°，从而实现侧1°偏角阶跃试验过程，如图4所示。具体试验测试步骤如表1所示，垂直加载位移为50 mm时为轮胎悬空无载荷状态，垂直加载位移为0 mm时则为测试的目标载荷。

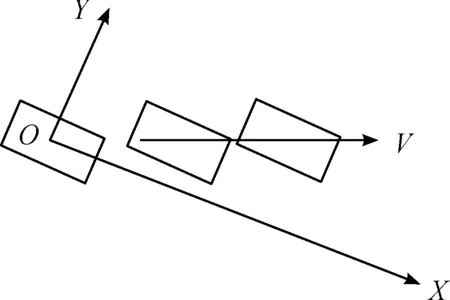
图4 轮胎在台架上的运动过程

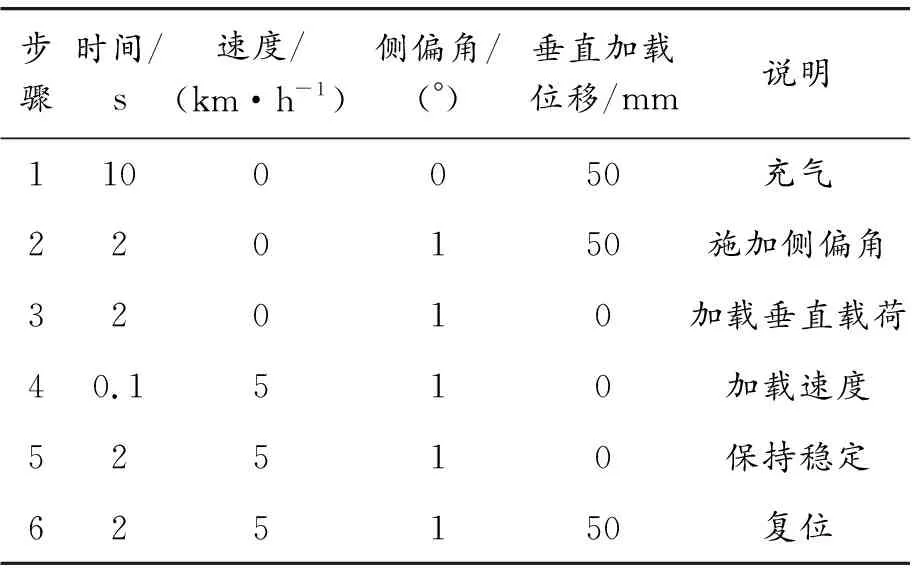
表1 先转角后加载法

2) 先加载后转角法。与先转角后加载法相比，最大的区别为先将轮胎加载到目标载荷后，轮胎在受载的情况施加1°转向角。然后迅速启动钢带到指定速度，钢带运动方向即为轮胎的速度方向，速度方向相对于大地坐标系X轴夹角为1°，从而实现侧1°偏角阶跃试验过程。具体试验测试步骤如表2所示。

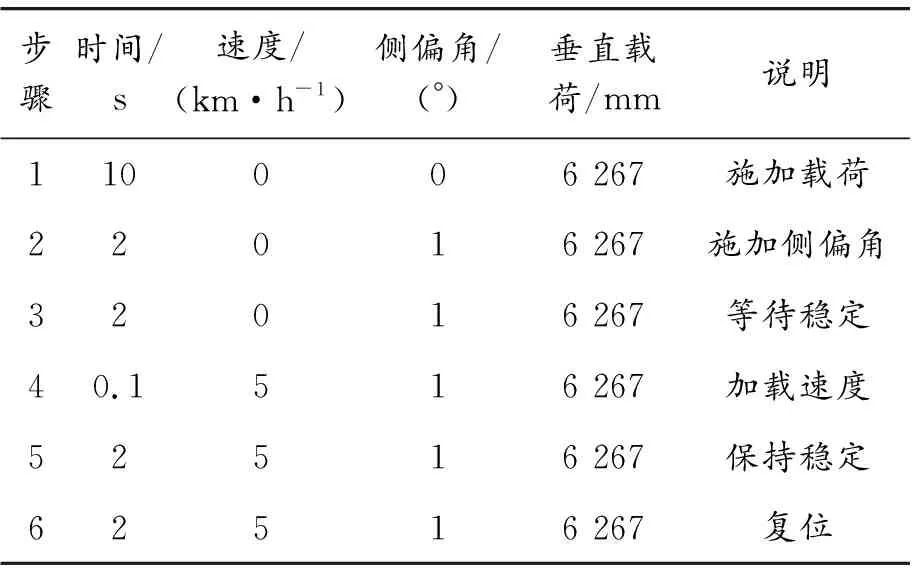
表2 先加载后转角法

2.2 转动角阶跃法

转动角阶跃与侧偏角阶跃不同，转角阶跃轮胎在大地坐标系XOY中无侧向位移，只存在横摆运动，转动角阶跃车轮的运动过程如图5所示。

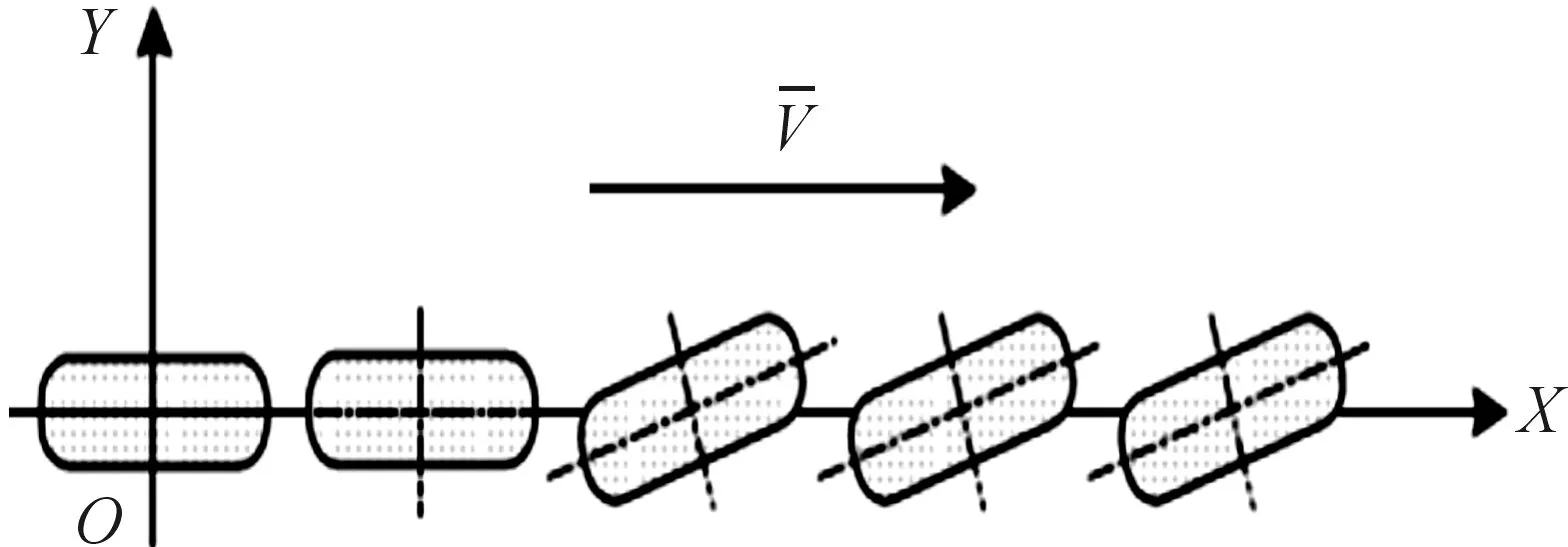
图5 转动角阶跃轮胎的运动过程

转动角阶跃法由于在轮胎滚动过程中有轮胎的转动，因此在轮胎侧偏运动的同时还叠加了转偏运动。纯转偏运动中轮胎只有横摆运动，轮胎中分面方向与速度方向保持一致，如车辆在低速过弯过程中轮胎的运动状态，此时转偏率等于路径曲率[13]。

(17)

而在转动角阶跃方法中，轮胎中分面方向与速度方向不再保持一致，轮胎在横摆运动的同时具有侧偏运动，此时的轮胎是转偏与侧偏的耦合,转偏率定义为[13]

(18)

转角阶跃下侧向力与回正力矩响应为：

(19)

综合本文2.1与2.2节可得，由于转动角阶跃中轮胎除了侧偏特性之外会引入转偏效应，故轮胎非稳态特性测量方法应选用侧偏角阶跃法。

3 侧偏松弛长度测量及其验证

侧向松弛长度的测量在中国汽车技术研究中心汽车工程研究院MTS FLAT TRAC CT Plus轮胎六分力试验台上依据本文设计的轮胎侧偏角阶跃方法进行。

图6 轮胎六分力实验台

松弛长度是指轮胎经过侧偏角阶跃后，侧向力上升至稳态值的63.2%时，轮胎所滚过的距离，试验结果如图7所示。

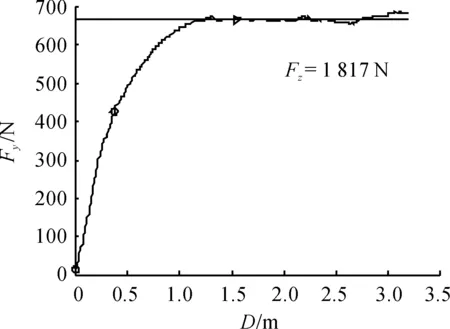
图7 某型号轮胎侧向松弛长度试验结果

采用侧偏角阶跃法中第1种方法(先转角后加载法)进行测试，选取3种不同载荷分别应用侧偏角阶跃方法与传统理论刚度法(侧偏刚度与侧向刚度的比值即为侧向松弛长度)所得结果如表3和图8所示。可以看出两种结果非常接近。

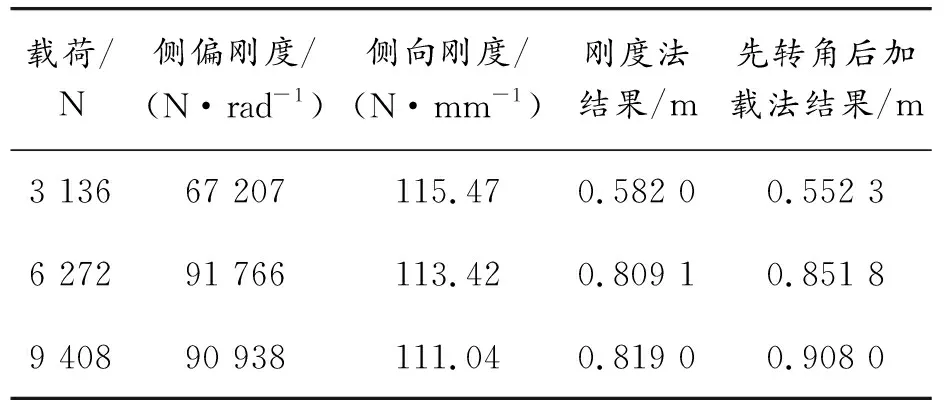
表3 先转角后加载法与刚度法结果对比

图8 先转角后加载法与刚度法结果对比

针对侧偏角阶跃法的第2种方法——先加载后转角法也进行了测试研究。选取同一条轮胎同一载荷进行测试，结果如图9所示。

图9 2种侧偏角阶跃法侧向力响应过程对比

方法2中由于先下压再转动轮胎至1°侧偏角，因此胎体具有扭转预变形，引起多余的初始侧向力，轮胎在开始滚动时要先抵消掉初始预变形，所以方法2会造成所测得的松弛长度结果变大。

将2种角阶跃法与刚度法测得的侧向松弛长度进行对比，可发现方法1所得结果更接近于刚度法结果，方法2所得结果明显大于其余2种方法所得结果，如表4所示。

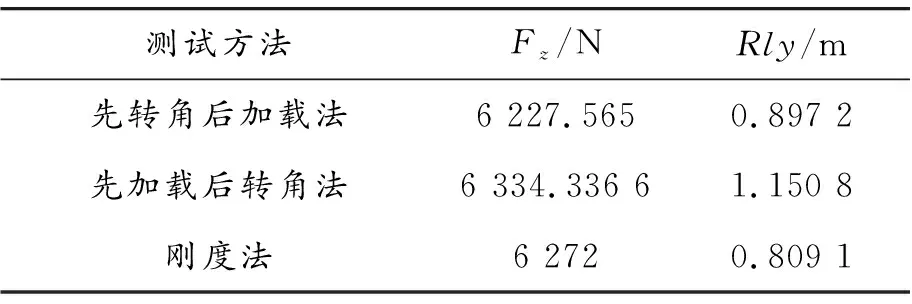
表4 同一载荷下2种角阶跃法与刚度法对比

4 结束语

通过本文的测试结果可以看出：先转角后加载法与理论刚度法计算出来的结果最为接近；而先加载后转角的方法由于先进行了加载再转动轮胎，因此胎体具有扭转预变形，引起多余的初始侧向力，轮胎在开始滚动时要先抵消掉初始预变形，所以方法2会造成所测得的松弛长度结果变大。综上所述，侧偏角阶跃法中的第1种方法即先转角后加载法可作为轮胎侧偏非稳态特性的准确测量方案。