一类广义部分Kloosterman 和的上界估计
2018-10-17胡双年刁天博尹秋雨牛玉俊吴宏锷
胡双年,刁天博,尹秋雨,牛玉俊, 吴宏锷
(1.南阳理工学院 数学与统计学院,河南 南阳 473004;2.郑州大学 数学与统计学院,河南 郑州 450001;3.四川大学 数学学院, 四川 成都 610064)
经典Kloosterman 和是指下述形式的指数和:

Kloosterman和的研究在数论中有着重要的意义。近年来,人们通过对Kloosterman和更加精细的估计,在许多领域取得了重要成果。 如Duke,Friedlander和Iwaniec在文献[9]中得到了著名结果:设f(x)=ax2+2bx+c∈Z[x],且D=ac-b2>0。则对任意给定h≠0,有

所谓部分Kloosterman和,是指如下形式的和式:
其中a,b为整数,m为正整数,gcd(a,m)=1,M,N是正整数,N≤m。x限制在与m互素的整数上取值,x*为不超过m的正整数,且xx*≡1 (modm)。若该和式是空和(即求和区间内没有元素),则我们规定该和等于0。对于部分Kloosterman和, 数学家们也做了许多研究[12-14]。同时,除了对经典部分Kloosterman和进行研究以外,数学家们还对其进行了推广,定义了一些新的和式。如部分双线性 Kloosterman和:
其中M1,M2,N1,N2,m为正整数,a为整数。
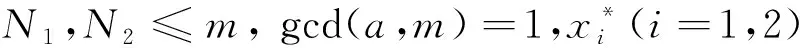
2014年Bourgain和Garaev[16]通过研究同余方程的解的个数,给出了一类部分Kloosterman和的上界估计。本文利用文献[17]中得到的一类同余方程解数的上界,给出一类新的部分多重线性Kloosterman和的估计,这推广了文献[16]中的部分结果。
定理1设n,k1,k2为正整数,n≥2,N为不超过m的正整数,Ki(i=1,…,n)为大正整数,并且对任意1≤j≤n-1,有2Kj 本节主要给出几个证明定理1时所需要的引理。 引理1[17]设n,k为正整数,且n≤2。对任意i=1,…,n,Ki为大正整数,并且对任意 1≤j≤n-1,有2Kj 引理2[16]设k为任意正整数。N为不超过m的正整数,I=[1,N]。设J2k(N)表示同余方程 满足xi∈I∩P的解的个数,其中1≤i≤n。则有 特别地,在Hölder不等式中取p=q=2,即得著名的Cauchy-Schuwarz不等式: 引理4对于任意复数z, 均存在一个依赖于z的常数ζz,使得|z|=ζzz,且|ζz|=1。 证明由复数的指数表示知,对任意复数z, 均有z=|z|eiθ。令ζz=e-iθ即得|z|=ζzz,且显然有|ζz|=1。 引理5对任意a∈Z, 有 证明注意到em(a)=1当且仅当m|a。因此利用等比数列求和公式,直接计算即得结论。 在这一节中,我们证明定理1。记定理1中不等式左边绝对值中的和式为S1,即 我们分两种情形讨论。 情形1k2=1。此时由三角不等式,有 情形2k2>1。此时由引理3(Hölder不等式)得 因此无论哪种情形,均有 (1) 由引理4知,存在一个依赖于q的复数|ζq|=1,使得 将上式代入式(1),有 |S1|k2≤ (2) 令集合 S:={x:x=p(1)p(2)…p(n),p(j)∈Ij∩P}, 其中Ij为引理1中定义的整数区间。对于任意整数λ, 0≤λ≤m-1,令Jk(λ)表示同余方程 满足xi∈S的解的集合。 对式(2)两边再次使用Hölder不等式(或者三角不等式)得 (3) 由Cauchy-Schwarz不等式可得 |S1|2k1k2≤ (4) 注意到 其中ζqi为依赖于qi的复数,且|ζqi|=1。因此 (5) 其中最后一个等式我们利用了引理5。将式(2), (5)代入(4),即有 |S1|2k1k2≤ 由引理1和引理2,可得 |S1|2k1k2≤ (6) 注意k1,k2为正整数,故2k1+2k2-2≤2k1k2。从而在式(6)两边开2k1k2次方即得定理1。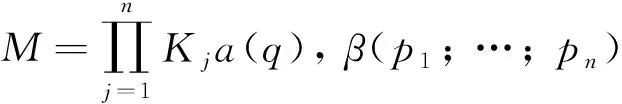

1 预备知识
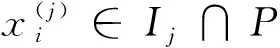
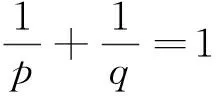
2 定理1的证明

