梯度下降算法在时间同步中的优化
2018-10-17刘云,肖雪
刘 云,肖 雪
(昆明理工大学 信息工程与自动化学院, 云南 昆明 650500)
无线传感网已被广泛应用于地下隧道监测系统中,但因隧道封闭空间的特点,在长距离范围内所部署的传感器无法通过外部信号进行联系,而传感器节点之间的时间同步对于实时分析和判定至关重要[1-2]。另因传感器节点资源受限的特点,内置硬件时钟由于不稳定的低成本晶体振荡器而产生时钟偏移,导致节点之间的同步丢失[3-7]。因此,每个传感器节点从中收集时间信息并构建网络全局时间函数(即逻辑时钟)[8-9],通过调整逻辑时钟的偏移和频率,使得任何时刻的误差最小化。
Wang等人提出了基于Voronoi图的泛洪广播时间同步算法(FBTS,Flooding broadcast time synchronization algorithm)[10],该算法的基本同步思想是在发送者和接收者之间记录具有时间戳的广播消息,并且通过K均值方法将数据聚集在一起,然后使用线性回归来消除数据偏离后的时钟偏移正常的误差范围。Yildirim等人提出了基于比例积分(PI)控制器的分布式时间同步算法(PISync,Synchronization algorithm based upon a Proportional-Integral(PI) controller)[11],节点通过在测量的相对偏移量上应用比例反馈(P)和积分反馈(I)补偿节点接收的参考时间的时钟偏移和时钟速度差来实现节点时间同步。
本文提出一种同步时钟的迭代方法,基于梯度下降法的多跳时间同步算法(GDTS,time synchronization algorithm based on the gradient descent),采用梯度下降算法[12]对误差函数的步长进行迭代更新,调整接收节点的逻辑时钟频率和偏移值,得到使误差函数最小化的逻辑时钟频率和偏移比值的最优估计值。仿真结果表明,与FBTS和PISync相比, GDTS可扩展性良好,收敛速度更快,同步误差更小。
1 系统模型
将传感器节点随机分布的地下封闭隧道抽象成一个基础数学模型,假定WSN 是一个拓扑结构图G=(V,E),顶点集合V={1,2,…,n}代表传感器节点的标识符,边集合E=V×V表示这些节点之间的双向通信链路,传输消息的任意节点u∈V,接收消息的节点v∈V,{u,v}∈E,邻居节点用Nu表示[13-16]。
在任何时刻t>t0,任意节点u硬件时钟表示为
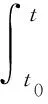
(1)
其中,fu(σ)∈[f0-fmax,f0+fmax],为硬件时钟振荡器频率,f0表示标称频率,±fmax表示频率偏差的上下限。时钟动态偏移表示为f(t)=f0+u(t),u(t)是[-fmax,fmax]中的均匀随机变量[15]。
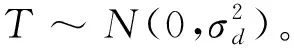
(2)
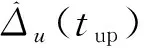
在无约束优化问题中,目标是最小化函数f(x),其中,f:Rn→R是可微分的凸函数。假设函数可解,因此存在最优解x*。由于f是可微分的凸函数,所以f(x*)=0。下降法产生一个序列xk+1=xk+αkΔxk,使得f(xk+1)
当搜索方向被确定为负梯度Δx=-f(x)时,所得到的算法被称为梯度下降算法[12]。设给定初始值x0,梯度下降法通过在负梯度-f(x)的方向上逐步地向下移动到较小的函数值,假定函数为凸函数,最后算法收敛到局部最小值。图1为梯度下降执行3次迭代过程。
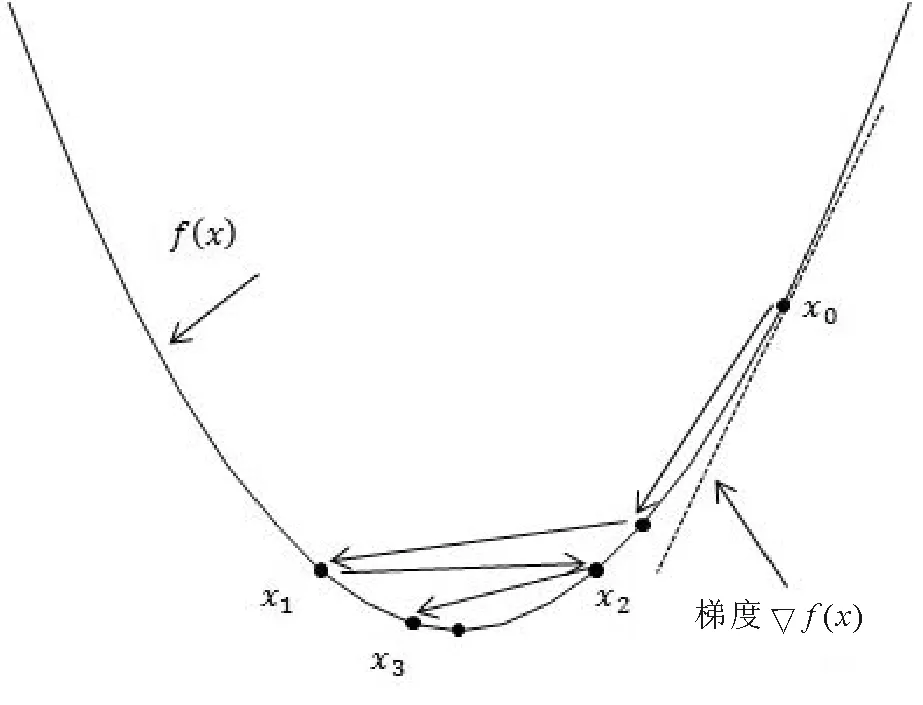
图1 梯度下降算法执行过程Fig.1 The execution of the gradient descent algorithm
2 GDTS算法分析
考虑两个传感器节点u和r的成对时间同步,其中,r是访问实时时间t的参考节点。假设节点r以B秒为周期传输实时消息给接收节点u。令th=Bh(h=0,1,…),表示从节点r到节点u的消息包接收次数,接收时钟lr(th)=Bh+Th,其中Th表示传输延迟。在任何消息包接收时间th=Bh时,u相对于参考节点r的同步误差计算为
eu(th)=lu(th)-lr(th)-Th=
lu(th)-Bh-Th。
(3)
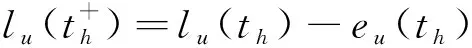
(B+Th+1-Th)。
(4)
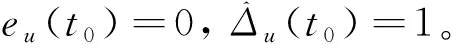
(5)
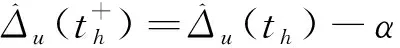
(6)

(7)
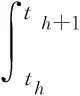
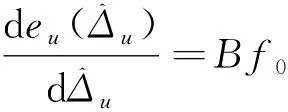
下面证明收敛性并计算稳态误差。
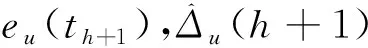
(8)
式(8)两边求期望得
E[x(h+1)]=
(9)
通过|A-λI|=0求矩阵A的特征值,即
解得
(10)
当且仅当|λ1,2|<1,矩阵A渐近稳定,得到渐近收敛。通过不等式(11)选择步长
(11)
得出系统收敛于渐近稳定点。
(12)
因此
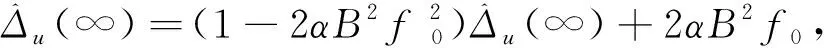
(13)
同理
(14)
式(14)表明同步时间最后实现稳态误差eu(∞)=0。
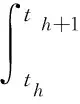
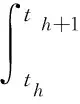
(15)
根据wh+1的定义和均匀随机变量u(t)得
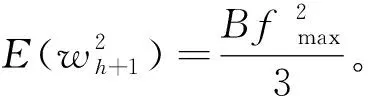
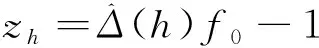
e(h+1)=
(16)
同理
(17)
令gh+1=Bf0+ωh+1,得
zh(1-2αBf0gh+1)-2αBf0gh+1+
同理
所以
(18)
由
{E[e(h+1)]}2=E[e(h+1)2]
得
var(e(∞))=
(19)
只要满足不等式(11),就会形成收敛。然而,α值越小,渐近方差越小。另一方面,收敛时间与式(10)中特征值λ2的大小成反比。因此,α越小,λ2越大,收敛时间越长。
GDTS算法多跳时间同步代码如下:
1) 一经收到〈lv,seqv〉,seqv>sequ;
2) seqv←sequ;
3)eu←lu←lv;
4)lu←lv;
5) 更新αu;
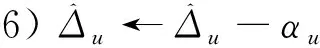
7)hu=kB,k∈N;
8) 如果u=r,那么sequ←sequ+1;
9) 广播〈lu,sequ〉。
步长α影响同步误差和收敛速度,长的恒定步长虽然收敛速度快,但稳态同步误差较大。另一方面,选择小的恒定步长,虽然稳态同步误差较小,但是收敛缓慢。当考虑到无线传感器网络的环境动态时,修改文献[11]中的自适应算法,自适应调整步长以实现快速收敛和较小稳态误差,步长表达式为
(20)
th是新同步信息的接收时间,e(th)是该时间的误差导数。如果e(th)和前一轮误差导数e(th-1)同号,即它们的方向相同,那么远离最优值需要加快调整尽快达到如果e(th)和e(th-1)反号,在附近摆动,为了更接近最优值,需要减慢调整。
3 仿真分析
为了验证本文所提算法的性能,将所提GDTS算法与类似的常规算法FBTS和PISync在Matlab 7.0中进行仿真分析,试验中对算法的收敛速度、同步误差及可扩展性3个性能指标进行了分析。
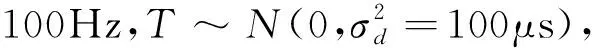

图2 频率随迭代增加变化图Fig.2 The relation between logical clock frequency and iterative times
在多节点的线性拓扑结构环境中对最大瞬时全局同步误差随时间的变化性能进行仿真分析,执行2×104s,与FBTS算法和PISync算法对比,GDTS算法的收敛速度最快,同步误差最小,如图3所示。
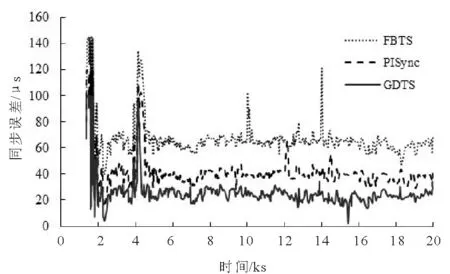
图3 瞬时误差随时间变化图Fig.3 The relation between synchronization errors and time
为了评估GDTS算法的可扩展性能,在不同的网络直径环境中将GDTS算与其他算法进行同步误差分析,每个网络进行10次仿真,每次仿真执行20万秒,最后将观察到的偏差值取平均值,3种算法的全局偏移随网络直径呈线性增长,但GDTS算法同步误差最小,如图4所示。
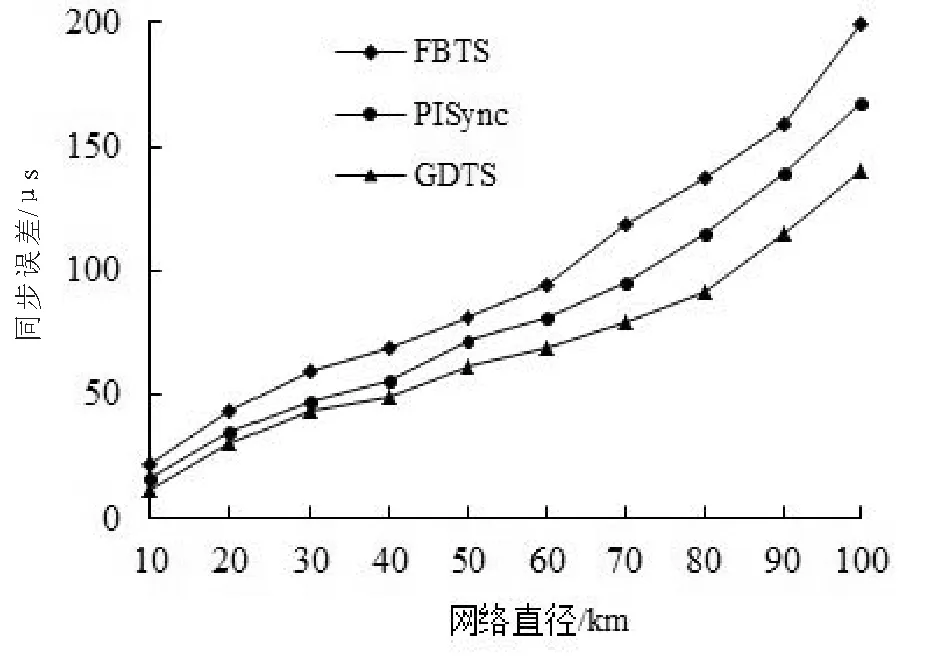
图4 同步误差随网络直径变化图Fig.4 The relation between synchronization errors and different network diameters
4 结 语
针对节点同步精度和收敛速度的问题,本文提出一种基于梯度下降法的多跳时间同步(GDTS)算法,通过采用梯度下降算法对误差函数的步长进行迭代更新,调整接收节点的逻辑时钟频率和偏移值,得到使误差函数最小化的逻辑时钟频率和偏移比值的最优估计值。仿真结果表明,对比FBTS和PISync算法, GDTS算法具有良好的可扩展性且收敛速度更快,同步精度更高。下一步的研究可以将所提出的方法与无线传感器网络中的占空比MAC协议相结合,研究其对能量消耗的影响。
