基于自主研发与引进再改造维度的后发创新模型与路径

陈 竹，邵明杰

（1.上海发展研究基金会，上海 200023；2.宁波大学 科学技术学院，浙江 宁波 315212）

0 引言

据世界银行的统计数据，近40年以来，中国是世界上经济增长最快的国家之一，尤其在1979—2007年间，中国经济年增长率高达9.873%，是同时期世界经济年均增长率的3倍[1]。关于中国经济为何能够长时间保持如此高增长速度的发展奇迹，诸多学者从比如高资本积累、技术进步与产业结构升级、体制改革、外资驱动等角度进行过讨论与解释。但这些解释都过于狭隘，正如郭熙保所言，他们都“没有触及问题的核心”[2]。中国社会技术经济的“后发优势”才是中国发展奇迹的最大推力，即科学技术上的后发创新优势成就了中国的经济高速增长。

从理论层面最早研究“后发优势”理论的学者是美国经济史学家Gerschenkron（1962），他认为后发优势就是后进者之于先进者在某一方面所具有的有利条件[3]；国内学者郭熙保（2009）从相对性、客观性、潜在性及递减性四个方面的特征定义了后发优势，并论证了“后发优势”与“追赶”的关系，他认为，有了后发优势就存在追赶的可能，追赶是一种经济学现象，而后发优势才是动力之所在[2]。有关技术层面的后发创新对经济增长的作用机制等理论问题也有诸多学者做过研究与论证：经济新增长理论代表学者Romer（1990）在技术进步外生增长的新古典模型基础上建构了技术内生化的增长模型，并强调了科学技术和人力资本在经济模型中的决定性作用[4]；Grossman和Helpman（1991）将技术能力作为经济增长全要素生产率的内生因子，建构了全要素生产率TFP的增长模型，将技术能力作为经济增长的内生决策变量，提高了经济决策的行为效率[5]。罗默与格罗斯曼的上述研究开启了技术内生增长模型的理论先河，而后美国学者埃弗雷特·罗杰斯提出的技术创新扩散模型则把内生技术创新模型的研究推向了一个新的研究高度[6]。在国内，刘志彪（2011）以我国制度创新背景下的创新型战略为研究对象，分析了我国从后发到先发的创新驱动战略理论问题[7]；傅晓霞，吴利学（2013）通过引入技术创新的知识生产函数，构建了基于后发国家的内生技术进步模型，并根据Barro等（2004）的研究成果[8]，对模型进行了数值模拟，给出了后发创新的转移动态机制[9]；刘红玉，胡钦如蓝（2017）通过对瑞典西斯塔（Kista）科学城和韩国大德创新特区作为后发创新城市典型案例，分析了雄安新区的后发创新驱动发展模式[10]。

现有研究对后发创新问题已经有了较为丰富的研究成果，但大都集中于宏观层面的机制研究或某一国家或地区的个案分析研究，鲜见后发创新内部要素分解的结构性研究。为此，本文将后发创新分解为自主研发与引进再改造两个结构性维度，以构建后发创新的经济学模型，从经济学层面讨论后发创新模型及其均衡路线，并试图得到一些有益的研究结论。

1 后发创新主体的生产函数及其最优解

本文考察后发创新主体在某一特定领域的创新行为。令创新主体在资源约束条件下实施生产决策，将资本、劳动及其相应的原材料转化为最终产品。假设F(t)为产品生产量，E(t)为后发创新主体在该领域的既有技术水平，M(i，t)为第i种原材料投入量，C(i，t)、L(t)为相应资本及劳动投入量。于是，根据Dixit,A.K&J.E.Stiglitz（1977）的研究结论，其生产函数为：，即最终产品的原材料投入总成本为所有投入材料成本的代数叠加和。令L(t)为t时间生产该产品的劳动力量，有L(t)=L(0)eh，即在假定人口增长率l外生给定的前提下假设生产该产品的劳动量为社会人口增长的正比例函数。再假设社会资本函数为C͂(t)=I(t)-λC(t)。其中λ为投入固定资产折旧率，于是，

其中，μ1∈(0，1)、μ2∈(0，1)、1-μ1-μ2∈(0，1)分别为第i种原材料、资本与劳动的产出弹性。为简化模型，令得到后发创新生产主体的最优决策函数为：

此处的p(i，t)为第i种原材料市场价格，r(t)为市场利率，为社会工资水平。式（2）分别对变量M(i，t)，C(i，t)，L(i，t)求导，得到：

可以看出，式（3）为第i种原材料市场需求函数，其提供厂家优化决策为：Max{M(i，t)}π(i，t)=[p(i，t)-1]M(i，t)，得到最优解为：

假设生产最终产品的各原材料投入呈平均分布，即令M(i，t)=M(t)/E(t)，C(i，t)=C(t)/E(t)。代入公式（1），得到生产该产品的最终生产函数为：

其中，a为相对技术差距。生产函数表明，该产品的最终生产量为投入要素的函数，其影响变量主要有μ1、μ2，即各投入要素的产出弹性对生产量产生重要影响。

于是得到第i原材料的投入量水平M(t)及其产出收益函数 π(i，t)：

本文研究的是后发创新行为，为此，做如下假定：第一，后发创新由自主研发和先进技术引进再改造两条途径实现；第二，综合创新成果为两路径成果（自主研发创新成果Gself(t)和技术引进再改造成果Gintro(t)）之和（注：下标self表示自身研发的，intro即为introduce,外来引进的，下同。），综合创新的成本投入也相应地包括自主研发成本投入inputself(t)和技术引进再改造成本投入inputintro(t)两个部分。接下来讨论后发创新主体的创新行为及其动态均衡解。

2 后发创新的可能性边界与综合创新效率

2.1 后发创新可能性边界函数

首先讨论后发创新的可能性边界。根据综合创新成果的内容组成及其投入成本结构，得到后发创新主体的综合创新成果函数Gc：

其中，E(t)、O(t)分别为当前该领域后发创新主体的生产技术水平及域外（Overseas）生产技术水平；ξ为自主研发的产出弹性；θself、θintro为技术的自主研发能力与引进再改造能力；进一步假设E͂(t)为总创新能力，直接表征上述综合创新成果Gc；ρ为自主研发技术对综合创新成果的贡献度，则1-ρ即为技术引进再改造对综合创新成果的贡献度；α∈（0，∞）为自主研发对技术引进再改造的替代弹性。于是，得到后发创新的可能性边界，如下：

可以看出，ρ∈[0，1]，ρ越大表明自主研发对综合创新贡献力越大，反之表明技术引进再改造对综合技术创新贡献越大。α∈（0，∞）为自主研发与技术引进的替代弹性：α＜1表明自主研发与技术引进为互补关系；α＞1表明自主研发与技术引进为替代关系；自主研发的产出弹性ξ∈（0，1），有1-ξ＞0为技术引进再改造的产出弹性，所以（1-ξ）越大表明，技术引进再改造对综合创新的贡献度越大，这表明，国内该领域现有技术与国外技术差距越大，实施技术引进再改造的效率就越高，技术的后发优势就越明显。

技术创新决策者旨在确定自主研发及技术引进再改造的成本投入量，以最大化当期创新收益。根据综合创新成果函数Gc及后发创新可能性边界函数，有：

据此得到自主研发与技术引进再改造的投入量方程，如下：

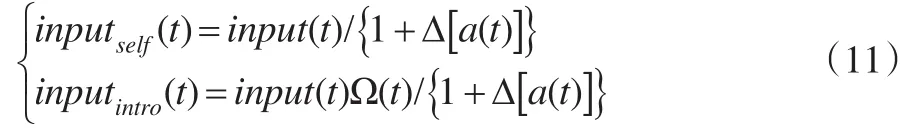
此处，a(t)=E(t)/M(t)，表征该领域内后发创新国家或地区之于技术发达国家或地区的相对技术差距；β=α-ξ（α-1）为导出替代弹性，其经济学意义与α相当，即表征自主研发与技术引进的互补或替代关系。

2.2 后发创新的综合创新效率函数

令相对技术差距下的综合创新效率为IE[ ]α(t) ，它描述了均衡条件下自主研发、技术引进再改造对综合技术创新能力的影响，故有：

联立式（9）、式（11）、式（12），得到综合创新成果均衡条件方程及自主研发效率函数e(t)：

对综合创新效率函数IE[α(t)]于参数相对技术差距a求导，得到：

可以看出，综合创新效率IE为后发创新主体相对技术差距a的增函数。这意味着：后发创新主体的相对技术差距越大，其综合创新效率就越高，这就从经济学上合理解释了“后发优势”的基本原理。但是这并不意味着相对技术差距越大，后发创新主体的综合创新成果最大。相反，相对技术差距越大表明后发创新主体的技术水平越低。相应地，对综合创新效率函数IE[ ]a(t)于参数θself、θintro求导，得到，这说明自主研发能力的提升以及技术引进再改造能力的提升均能提高综合创新能力与创新效率。

3 后发创新动态均衡及其各参数说明

令创新收益为Π(t)，它是所有原材料i投入收益的函数，根据上述第i种原材料的产出收益 π(i，t)函数式（6）可得：

由于投入成本的非负性，即input(t)=inputself(t)+inputintro(t)＞0，根据均衡最优化条件，创新收益等于创新投入成本，所以E͂(t)Π(t)/input(t)=1。于是根据式（13）和式（16）得到后发主体创新收益与创新投入的函数关系，如下：

最优化一阶求导，得到后发创新投入的动态均衡方程：

令i(t)=I(t)/[E(t)L(t)]其中：i=c，input，f,分别表示资本投入量、研发投入量以及该技术产品的最终产出。于是，式（17）整理得到：

上述已设λ为投入固定资产的折旧率，l为投入的单位劳动力。可以看出，不管是从后发创新综合效率函数式（12）、式（14），单位投入创新收益的动态均衡函数式（16），还是从后发创新投入动态均衡方程（17）、方程（18）等后发创新均衡模型，都可以看出，影响后发创新综合效率IE[a(t)]及后发创新收益π(t)、成本input(t)的主要参数有ξ、ρ、α、θself、θintro、β。其中，ξ为研发投入成本的产出弹性，ρ为自主研发对综合创新效率的贡献度，α为自主研发与技术引进的替代弹性（由前述，β的性质与α类似，故此处只列出α），表征了两种创新路径的或替代或互补的关系，θself、θintro为技术创新主体的自主研发能力与技术引进再改造能力。

4 结论与讨论

本文基于自主研发与引进再改造两个维度，对后发创新模型进行了构建，并通过经济学最优化模型，对其均衡路线做出了讨论。通过以上分析,本文认为：

第一，后发创新要在自主研发与技术引进再改造两个方面保持动态平衡。自主研发贡献度ρ对综合创新效率产生重要影响。自主研发贡献度越大，创新主体对自主研发的投入必然增加，相应地就会降低对技术引进与再改造的重视程度，影响对现有先进技术吸纳能力的提升。所以，后发创新主体应该在自主创新与技术引进再改造两个层面的能力提升上保持动态平衡。

第二，要着重自主研发的创新投入水平，避免陷入技术“拿来”的路径依赖。技术创新主体的自主研发能力θself的提高将促成综合创新效率的增强，进而缩小与域外先进技术主体的相对技术差距。但自主研发能力θself对后发创新主体的创新成本投入结构的影响主要视自主创新与技术引进的相互关系，如果两者互为替代则提高自主研发能力会降低技术引进的投入比重，如果两者为互补则提高自主研发能力将会提高技术引进的投入比重，促使自主研发能力与技术引进再改造能力的同步增长。相对应地，从后发创新主体创新投入的动态均衡方程（18）可以看出，自主创新投入与技术引进再改造投入替代性较强（在一定程度上可能表现为互斥），这意味着，技术引进再改造能力θintro的提高将在一定程度上抑制技术创新主体自主研发能力θself的提高，因为由于技术引进与自主研发替代效用的存在，技术引进再改造能力的提高会使后发创新主体形成一种技术“拿来”的路径依赖，无形强化后发创新主体与先进技术主体的技术差距。因此，后发创新要着重加强自主研发的创新投入水平，避免陷入技术“拿来”的路径依赖。

第三，要根据社会经济发展的不同阶段，对后发创新路径实施动态调整。后发创新主体的技术创新路径选择主要取决于自主创新与技术引进再改造两者的或替代或互补的关系。从综合创新成果Gc的函数表达式（7）及其可能性边界函数式（8）可知，后发创新成果由自主创新成果及技术引进再改造成果两部分组成。两种创新成果之关系并不会显著影响后发创新主体综合创新成果的绝对值，但从综合创新效率IE[ ]a(t)函数式（14）可以看出，自主创新与技术引进的关系变量ε能显著影响综合创新效率IE[ ]

a(t)。这意味着，两者之关系将显著影响后发创新主体的创新投入结构：如果自主创新与技术引进的关系处于强替代关系上，则后发创新主体更愿意实施技术引进投入，利用域外先进技术实现其技术进步，但这种技术创新策略常受制于人；反之，如果两者处于强互补性阶段，则自主创新占优，后发创新主体更愿意实施自主创新投入，使自身技术带有较强的自主研发特点，而不至于受制于人。