基于改进的密度峰值算法的K-means算法
2018-10-17杜洪波白阿珍朱立军
杜洪波,白阿珍,朱立军
(1.沈阳工业大学 理学院,沈阳 110870;2.北方民族大学 信息与计算科学学院,银川 750021)
0 引言
数据的爆炸式增长是大数据时代到来的一个显著性的标志。虽然,数据量是大的,但是,数据中蕴含的知识只是其中很小的一部分。如果能将数据中蕴含的知识提取出来加以利用会带来重大价值。传统的工具和软件技术在处理大规模数据时已经显得力不从心,因此,为了找出数据中有价值的知识,人们经过不懈地探索,发现了数据挖掘技术。而聚类分析是该技术的一个研究热点,并且,往往用来做分类工作。
聚类分析(ClusterAnalysis)又被称为群分析,为无监督学习,并且,它无需任何先验知识就可以发现数据的分布模式[1,2]。“物以类聚”为它的关键特征。自聚类出现以来,出现了许多不同类型的算法来满足聚类的不同需求和挑战,其中包括基于划分的聚类算法[3]、基于层次的聚类算法[4]、基于密度的聚类算法[5]、基于网格的聚类算法[6]和基于模型的聚类算法[7]以及近几年提出的新的聚类算法[8]。
K-means算法是典型的基于划分的聚类算法。由于其优点而在实际中被广泛应用[9],但是,其也存在着一些缺点。学者们根据应用环境不同以及实际要求,以经典的K-means算法为基础,针对其存在的多种缺陷,提出很多改进算法。
针对算法对初始聚类中心敏感的不足之处,薛卫等[10]提出一种空间密度相似性度量K-means算法,该算法利用可伸缩空间密度的相似性距离来度量数据点之间的相似度,并将密度和距离一起当作选择初始聚类中心的相关因子,以及根据类内距离进行迭代的一种新的类中心迭代模型,实验证明,该算法可得到更加合理的初始聚类中心。贾瑞玉等[11]基于密度的原理,通过对数据对象密度计算方式的再定义,并利用残差分析从决策图中自动确定K值和初始聚类中心。考虑到K值选择的盲目性,张承畅等[12]提出一种基于密度的K-means改进算法,此算法定义了权值积,它是样本密度、簇内样本平均距离的倒数以及簇间距离三者的乘积,并通过最大权值积法解决最佳K值确定以及初始聚类中心问题。陈书会等[13]基于人工鱼群原理提出了一种人工鱼群和K-means相结合的IAFSA-KA算法[13]。为了解决运用欧式距离度量相似性而导致只能发现球状簇的问题,肖琦[14]利用GSAGSA肘形判据、距离代价函数等算法优化确定最优聚类K值,并依据密度参数来提取合理的初始聚类中心。
DPC算法是2014年由AlexRodriguez和Alessandro在Laio Science上发表的一篇名为《Clusteringby fast searchandfindofdensitypeaks》的核心算法,文章一经发表就引起了众多学者的关注。该算法简洁而优美,并且其能够快速发现任意形状数据集的密度峰值点(即聚类中心),并且,能够对样本点进行高效率地分配以及有效地剔除离群点,容易确定参数,适用于大量数据的聚类算法。
DPC算法[8]对初始聚类中心的确定很有针对性,因此,该算法作为一个关键步骤而应用到数据挖掘中[15]。但是,该算法也存在一定的缺陷。谢娟英等[15]基于K近邻思想提出的K-CBFSAFODP算法能够很好地解决DPC算法密度度量准则不统一、一步分配策略的缺陷。Wang等[16]提出了一种通过使用原数据集潜在的熵的新方法来自动提取截断距离dc的最佳值,通过实验证明,利用数据场获得的截断距离dc比人工经验获得的聚类效果更好。关晓惠等[17]基于密度原理来确定聚类中心及其样本点分配,弥补其需人为操作的缺陷。褚睿鸿等[18]在原有的DPC算法中引进一个合理的参数K,并将改进的DPC算法进行集成,从而自动完成聚类中心的选取,从而获得最后的聚类结果。
实际上,每种聚类算法各有其适用范围,并有其独特的优势以及一定的不足之处,通过众多学者的研究发现,将某些聚类算法结合起来使用可以有效地提高聚类效率或准确率。
因此,为了克服K-means算法随机选取初始聚类中心的不足之处,本文提出一种基于改进的DPC算法的K-means聚类算法。首先,运用改进的DPC算法来选取初始聚类中心;然后,运用K-means算法进行迭代得到聚类结果,从而,弥补了K-means算法随机选取初始聚类中心可能导致易陷入局部最优解的缺陷;并且引入熵值法[19]计算距离优化聚类。
1 熵值法计算赋权欧式距离
为了更好地分析各个数据对象之间的差异,本文利用信息熵来计算各数据对象的赋权欧式距离。
在信息论中,信息熵是对不确定性的一种度量。信息量越大,不确定性越小,熵越小,权重越大;信息量越小,不确定性越大,熵越大,离散程度越小,权重越小[20]。它可以计算指标的离散程度。如果计算出的结果越大就说明该指标对综合评价的影响(即权重)越大[21]。故,可运用信息熵计算各指标的权重,为综合评价提供理论依据。算法的实现步骤如下:
假设数据集X有m个对象和n维属性:


其中,xij是属性值,Mij是数据对象xi第j维属性所占比重值。
步骤2:按照等式(2)和式(3)分别计算第j维属性的熵值与权值:
熵值:
步骤1:首先标准化数据对象的属性:

权值:


用赋权欧式距离度量相似度,可以精确得出各数据对象彼此间的差异程度,进而提高聚类精确度。
步骤3:计算赋权欧氏距离的公式如下:
2 K-means算法
K-means算法是由MacQueenJB在1967年首次提出的,是硬聚类算法。它的评价指标是距离,距离越小越相似,而最终目标是获得紧凑并且独立的集群[22]。
K-means算法中的K值表示要聚类数据集的聚类数,而means代表类簇均值。也就是说,该算法使用一个均值代表一个类簇的聚类中心。并且,该算法用欧式距离来度量数据对象之间的相似性,采用误差平方和来评聚类效果。
K-means算法的目标函数为:
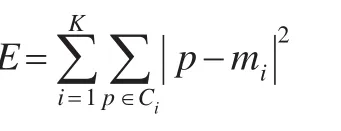
其中,E是数据集中的所有数据对象的平方误差之和,p是数据集中的数据对象,mi是集群Ci的中心。
K-means算法描述如下:
输入:包含n个对象的数据集和簇的数目K。
输出:满足目标函数E最小值的K个簇。
步骤1:从n个数据对象中随机选择K个对象作为初始聚类中心;
步骤2:对于剩余对象,按照其与聚类中心之间的距离,依据就近原则分配到相应的类簇;
步骤3:计算每个类簇的新均值,即新的类簇中心;
步骤4:回到步骤2,循环,直到不再发生变化。
由以上可知,K-means算法的特点是两阶段迭代循环、将数据对象的划分不再发生变化作为循环终止条件。
3 改进的DPC算法
3.1 DPC算法
DPC算法是以聚类中心点由一些局部密度较低的数据对象所包围,并且与任何具有较高局部密度的数据对象之间的距离相对较大为假设基础。此外,为了防止一些分散的离群点被强制分配到类簇当中,从而造成聚类后类簇的边界不清晰,进而影响聚类的效果,本文为每个类簇确定了一个边界区域,再把数据对象进一步划分为核心部分和光环部分(也就是噪声)[8]。该算法首先定义了两个量:局部密度ρi和距离δi。
对于数据对象i局部密度ρi:有cut-offkernel和Gaussiankernel两种定义方法。
(1)cut-offkernel(对于较大规模数据集):


其中,dij为数据对象i和j之间的欧式距离,dc为截断距离,由人工确定,通常将所有数据对象两两之间的距离按升序排列后前2%位置的数值距离作为截断距离。
数据对象i的距离:
其中:

(2)Gaussiankernel(对于较小规模数据集):)

对于每个数据对象i,首先,需要计算局部密度ρi和距离δi,然后,根据计算得到的这两个值画出一个二维平面决策图。
构造决策图:

将γi进行降序排序,并以数据对象的下标为横坐标,γ值为纵坐标构造决策图,如图1。可以发现,γ的值越大则数据对象是聚类中心的可能性就越大。而且,从图1中可以发现,不是聚类中心的数据对象的γ值比较平滑,而在聚类中心的γ值转换到非聚类中心的γ值时有一个非常明显的跳跃,并且,无论是肉眼还是数值的检测这个跳跃都能很容易判断出来。从而,这个跳跃就是聚类中心与非聚类中心的分界线。

图1 γ决策图
当聚类中心选定后,对于剩余的数据对象则采用一种“跟随”策略,归属到密度比其密度大的最近邻所属的类簇中,得到最终的聚类结果。
3.2 改进的DPC算法
由于在DPC算法中,局部密度ρi和距离δi的计算依赖于截断距离dc,而文中的截断距离dc是通过人工设置的,它是人工经验方法,即使dc的选择具有鲁棒性,但是依旧缺乏理论依据。因此,本文介绍了一种选择最优dc值的方法[23]。
步骤如下[23]:
对于数据对象i,令向量:

其中,dij(i,j=1,2,…,n;i≠j)为数据对象i到数据对象j之间的赋权欧式距离。将向量li按从小到大的顺序进行排序,从而得到向量ci,即则数据对象i的截断距离dci就可以定义为:

其中,max(ai(j+1)-aij)是向量ci中相邻的两个元素之差的最大值。
由图2可以看出,同一类簇的数据对象之间的距离差距比较小,而不同类簇的数据对象之间的距离差距比较大,所以,在向量ci中,有两个相邻元素的差距会较大[23],即:

其中,aij=a,ai(j+1)=b。由图2可认为数据对象是从一个簇跳跃到了另一个簇中,如果找到最大的差值则可找到理想的截断距离dci,即:
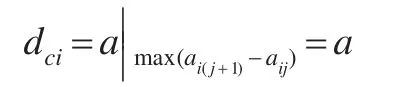

图2 截断距离决策图
本算法对于存在离群点的情形也适用,如图3所示。

图3 有离群点的情况
由图3可知,在升序排序后获得的向量ci中,相邻两个元素之差的最大值为:
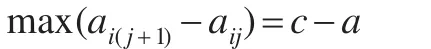
即aij=a,ai(j+1)=c。由式(9)可知,数据对象i的截断距离为:
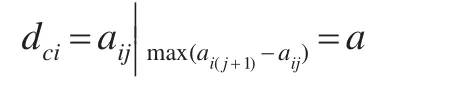
各数据对象i均分别有dci与其照应,因此,它们组成了一个集合Dc:
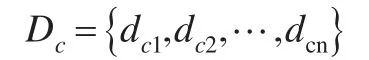
为了减少集群边界上点和离群点的影响及避免dc过大,dc应取集合Dc的最小值,即:

这种确定截断距离dc的方法与密度指标和距离指标相同,是基于数据对象之间的距离得到的,所以,不会增加额外的计算负担。将式(10)带入求各数据对象i的局部密度ρi的等式(5)或(6)和距离δi的等式(7),然后,求得ρi和δi,从而完成数据对象聚类过程。这种改进的方法为dc的选择提供了依据,而且算法简单、易实现。
4 改进的K-means聚类算法
针对K-means算法随机选择初始聚类中心进行迭代可能导致不稳定的聚类结果,本文提出一种改进的K-means算法,本文首先通过改进的DPC算法来选取聚类中心作为K-means算法的初始聚类中心;然后,使用K-means算法进行迭代,并且引入信息熵计算赋权欧氏距离[19],以便更准确地规范各对象之间的差异程度,从而更好地聚类。
本文算法描述:
输入:含有n个数据对象的数据集合。
输出:满足目标函数最小值的K个簇。
步骤1:使用熵值法计算各数据对象之间的赋权欧氏距离dij,并令dij=dji,i<j,使其成为一个完整的矩阵;
步骤2:确定截断距离dc;
步骤3:根据确定的截断距离dc,并利用DPC算法中的方法计算每个数据对象i的ρi和δi;
步骤4:根据γi=ρi×δi,i=1,2,…,n,选择聚类中心,γ越大越可能是聚类中心;
步骤5:确定聚类中心cj,j=1,2,…,K与K的值;
步骤6:计算剩余每个数据对象与各类簇的中心的距离,并将每个数据对象赋给距其最近的类簇,进行划分;
步骤7:重新计算每个新簇的均值作为新的类簇中心;
步骤8:计算目标函数值;
步骤9:直到目标函数不再发生变化,算法终止;否则,转步骤7。
5 实验分析
5.1 实验描述
为了验证本文算法的有效性,选取UCI数据库的Iris和Wine作为实验数据集。实验数据集的构成描述如表1:

表1 实验数据集的构成描述
并与传统的K-means算法以及文献[16]中提出的算法K-CBFSAFODP进行了对比。
5.2 实验结果分析
对于选择的UCI中的数据集运用K-means算法、K-CBFSAFODP算法以及本文提出的算法进行聚类以后发现,本文提出的算法在聚类时间、聚类误差平方和和聚类的准确率方面有所提升。
将本文算法得到的实验结果与Iris数据集的实际中心进行比较,如表2所示:

表2 本文算法实验结果与Iris数据实际中心比较
从表2可以看出,本文算法得到的聚类中心与Iris数据的实际中心非常接近,从而能够说明该算法对Iris数据比较有效。同理,该算法对Wine数据也比较有效。
本文算法的误差平方和优于K-means、K-CBFSAF ODP算法,迭代次数优于传统的K-means算法,如表3所示。
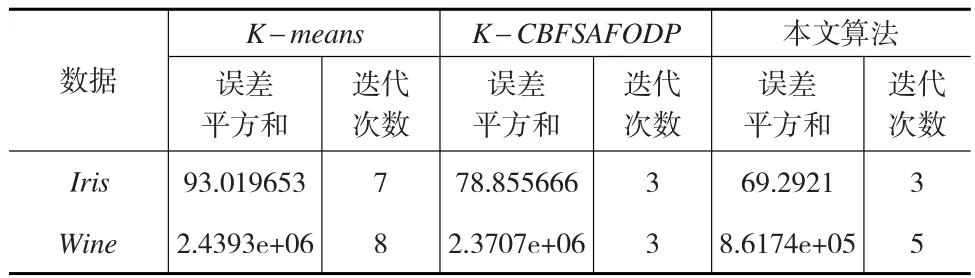
表3 误差平方和及迭代次数的比较
由表3可以看出,在选择的数据上本文算法的误差平方和、迭代次数明显优于传统的K-means算法。而与K-CBFSAFODP算法相比,在Iris数据上,虽然两算法迭代次数相等,但是误差平方和稍微优于K-CBFSAFODP算法的误差平方和。在Wine数据上,本文算法的迭代次数虽然比K-CBFSAFODP算法的大,但是其误差平方和却明显优于K-CBFSAFODP算法。
聚类准确率也是衡量聚类结果的重要性指标。而三种聚类算法在UCI数据集上的聚类准确率的比较,如表4所示:

表4 聚类准确率的比较 (单位%)
从表4中可知,在聚类准确率方面,本文算法明显优于传统的K-means算法,同时,在Iris数据上本文算法优于K-CBFSAFODP算法,但是,在Wine数据上却明显优于K-CBFSAFODP算法。从而,能够充分说明本文提出的算法具有较好的聚类效果。
6 结论
传统的K-means算法随机地选择初始聚类中心进行迭代,可能导致不稳定的聚类结果,并且算法中的K值需要事先人为确定,因而导致限制了该算法的应用。本文提出的基于改进的密度峰值优化初始聚类中心的K-means算法能够很好地解决前文叙述的两点不足之处。利用改进的密度峰值算法选取初始聚类中心,并根据决策图决定聚类个数K,这弥补了K-means算法的上述不足之处,接着利用K-means算法进行循环迭代,进而得到聚类结果。实验表明该算法能够得到较好的聚类结果。
