基于云理论的不确定性推理模型在径流预测中的应用

邵年华

(深圳市西丽水库管理处，广东 深圳 518055)

水文模拟预测是流域防洪抗旱、水资源规划的重要依据，也是水资源有效利用和社会经济可持续发展不可或缺的手段。随着水文数据获取能力和计算机性能的提高，各种水文模型得到快速发展。但大多数水文模型都是基于确定性理论的预测，往往回避了不确定性问题。受气象因素和地理因素影响，水文过程必然是一个复杂的动态过程，对水文预测也将存在普遍的不确定性[1]。因此，研究水文预测的不确定性对于完善水文模拟与预测理论、合理开发水资源都具有重要理论价值和现实意义。

水文水资源系统中的不确定性主要包括模糊性和随机性等。研究方法有模糊理论和概率分析方法，但这些方法大多孤立的应用，很少综合在一起。而水文系统往往是各种不确定性因素的综合体，因此考虑多种不确定性的、基于贝叶斯概率理论的贝叶斯概率水文预报模型成为研究水文系统不确定性的主要方法[2-4]。但由于该模型的结构复杂，参数众多，而不利于在实际中推广应用。针对当前存在的问题，本文把基于不确定性理论的云推理模型引入水文预测领域。该模型可以把不确定性概念的模糊性和随机性有机地结合起来，利用期望Ex、熵En和超熵He表征定性概念，实现不确定性语言值与定量数值之间的自然转换，以期能拓展水文不确定性理论，丰富水文预测方法。

1 云模型原理

假设u(x)取值于区间[0，1]，云即为U到区间[0，1]的映射，即u(x):U→[0,1]，∀x∈U，x→u(x)。

云不确定性概念可通过计算云的期望Ex、熵En和超熵He等数字特征来反映其整体特性[6]。云的Ex、En、He可将模糊性和随机性统一起来，在定性概念和定量数值之间形成一种相互联系的映射关系。

2 云发生器实现

云的实现可通过软件和固化成硬件来完成，即云发生器(Cloud Generator，简称CG)。它是在定性概念和定量数值之间建立的一种相互联系的映射关系，是进行不确定性推理的基础。正态云模型是云的基本模型，因此正态云模型为研究云发生器的常用模型。见图1。

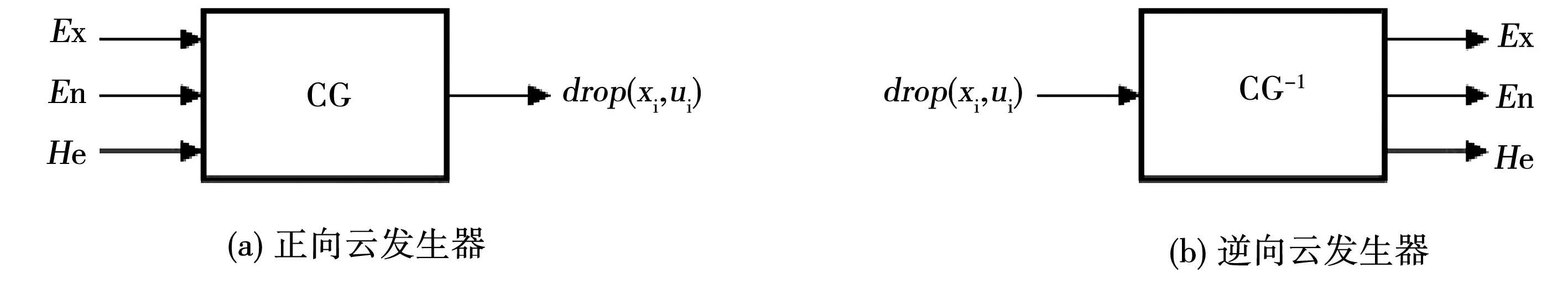
图1 云发生器Fig.1 Cloud Generator

2.1 正向云发生器

2.2 逆向云发生器

2.3 X与Y条件云发生器

云还可以生成特定条件下的云发生器。已知正向云数字特征值(Ex，En，He)，在给定特定条件x=a，则生成X条件云发生器；若给定特定条件是u(x)=u(a)，则生成Y条件云发生器，连接二者，可生成单条件规则发生器。见图2。

图2 不同条件下的云发生器Fig.2 Cloud generator under different condition

3 云推理过程

云模型的云推理是以不确定性理论为基础，并以所表达的一个概念与多个概念之间因果逻辑关系为推理规则。这种推理规则可以演绎成一对一、一对多、多对一、多对多等形式，对应于云模型即可建立成有单条件单规则、单条件多规则、多条件单规则和多条件多规则4种模式的不确定性推理过程。

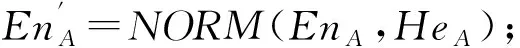
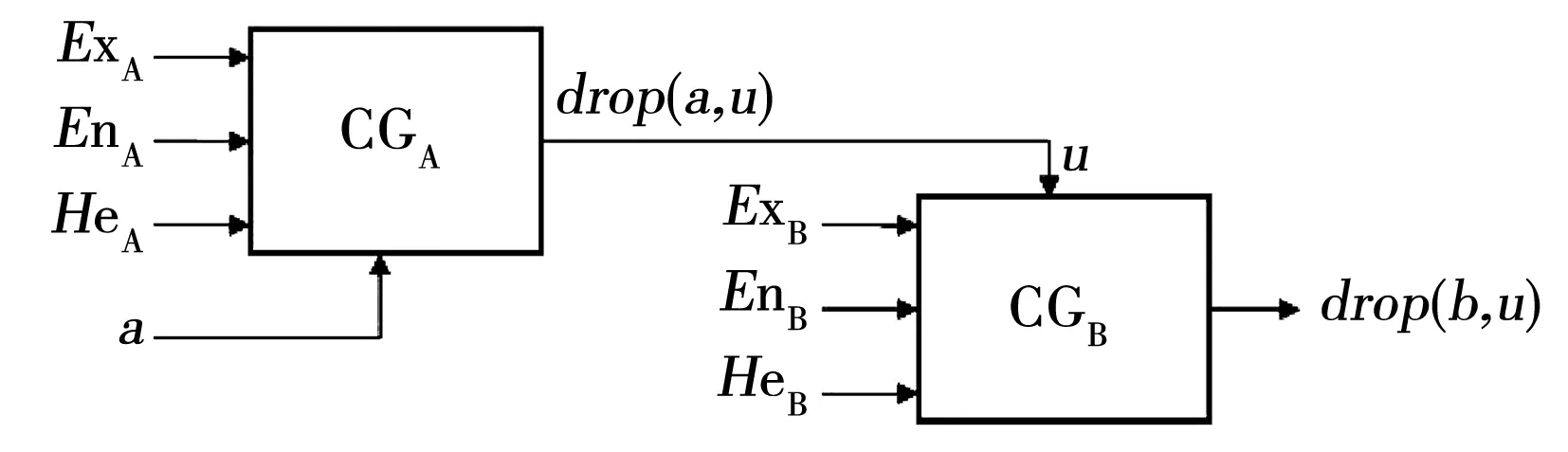
图3 单条件规则云发生器Fig.3 One single condition and rule cloud generator

当存在多条规则时，可根据a来确定合适的规则。利用隶属概念判定的方法有极大判定法和随机判定法。极大判定法利用特定值对所有规则集中规则隶属程度的大小，来确定最大隶属程度的规则作为隶属概念。随机判定法利用特定值在所有规则集中规则隶属程度较大的几个中随机选择隶属规则。

4 基于云模型的时间序列预测

4.1 前件云、后件云和趋势云的确定

从给定的时间序列数据中挖掘出m组规则数据，将规则数据输入逆向云发生器可得到前件云A(ExA，EnA，HeA)与后件云B(ExB，EnB，HeB)，m组前件云与后件云组成预测规则集合{A1→B1,A2→B2,…Am→Bm}。

根据惯性定理，在短暂的时间内时间序列数据具有相对稳定性，可从数据中挖掘当前趋势作为预测信息。但数据所包含的当前趋势只能反映未来的可能性，因此不能完全以当前数据计算的数值作为最终预测结果。当前趋势的信息应包含不确定性且遵循当前数据的分布规律，因此它应当表示为定性趋势而不是定量数值[8]。云模型可满足这种定性趋势与定量数值的转换，将预测值的前t个数据作为趋势数据输入逆向云发生器，即可得趋势云I(ExI，EnI，HeI)。

4.2 选择某一预测规则Ai→Bi，确定预测前件云与后件云

将预测规则集中的m个前件云分别构造X条件云发生器，代入特定值a分别得到m个输出u，它们分别反映了u对m个前件云的确定程度。通过最大隶属度原则可以找到最大ui，则Ai即为预测前件云。如果存在两个以上最大值u，可以任选其中一个。Ai确定后，对应的Bi即为预测的后件云[9]。

4.3 确定预测云，构造新的预测规则

若给定两个相邻的云模型C1(Ex1，En1，He1)和C2(Ex2，En2，He2)，可以通过下面公式综合这两个云模型得到综合云C(Ex，En，He)：

(1)

En=En1+En2

(2)

(3)

通过式(1)-式(3)的计算，可整合后件云Bi和趋势云I，形成预测云St。St的期望值在趋势云和后件云之间，熵是它们熵的总和，这样预测云就可计算出更多可能的预测结果。

通过构造可组成新的语言规则Ai→St，利用预测云St及相应的确定度ui构造Y条件云发生器，则Y发生器的输出值b即为预测值。

5 云模型在径流预测中的应用

和田河是塔里木河三大源流之一，发源于喀喇昆仑山和昆仑山，北流入塔里木盆地，穿过塔克拉玛干大沙漠，汇入塔里木河。和田河有二源，西源喀拉喀什河(简称“喀河”)发源于喀喇昆仑山北，东源玉龙喀什河(简称“玉河”)发源于昆仑山北坡，并在出山口处分别设有乌鲁瓦提和同古孜洛克水文站(简称“乌站”和“同站”)[10]。本研究选取玉河同站1956-2002年共46个实测年径流数据进行模型预测分析。其中，云模型训练样本为1956-1992年36个实测年径流量， 1993-2002年共10个实测年径流量数据作为验证模型预测效果样本。

对选取玉河同站1956-2002年共46个实测年径流数据序列进行归一化处理，得到序列R={r1,r2,…,r46}。在云推理过程中，考虑相邻年份对未来年份径流量的影响，分别将归一化处理后的1956-1991年和1957-1992年径流量数据作为推导相邻年份不确定性规则的输入样本E及输出样本O，即得到数据组合(ei，oi)，i=1，2，…，31。

根据径流丰枯变化特性，可以利用模糊模式识别对序列E进行分析，挖掘出丰水年、平水年、枯水年三组规则数据。O序列数据做相应于E的分类。将3组规则数据中的输入样本数据和输出样本数据分别输入逆向云发生器生成规则前件云和后件云，这3条对应规则反映了相邻年份径流量之间的关系，规则数字特征见表1。同时，考虑历史数据变化趋势对未来径流量的影响，将预测年份前5年的数据代入逆向云发生器生成趋势云，根据式(1)-式(3)合并趋势云与后件云，最后生成规则的预测云。

表1 云模型数字特征Tab.1 The digital character of cloud model in rules

在得到三则规则后，将预测值上一年径流量代入，并通过最大隶属度原理，确定预测规则，最后根据发生器计算出未来的年径流量。在演算过程中，因进行不确定性推理，结果在一个允许范围内会不同。本文进行10次演算后，对模型计算结果进行反归一化处理，取期望值作为最终的径流量预测值(表2)。

表2 云模型与LS_SVM模型的年径流量预测结果比较Tab.2 Comparison between measured and predicted annual runoff of cloud model and LS_SVM model

本文还利用最小二乘支持向量机(LS_SVM)模型建立玉河年径流量预测模型，并与云模型预测结果进行比较。两种模型预测结果见表2和图4。从表2可知，云模型预测结果中较大误差发生在1993和1994年，分析可知1993年径流量为整个系列的极小值，1994年径流量为整个系列的极大值，说明云模型对极值的模拟效果略差。LS_SVM模型与云模型预测结果的平均误差分别为12.3%和11.9%，说明云模型的整体模拟效果略好于LS_SVM模型。从图4中可见，LS_SVM模型对极值部分模拟的较好，而云模型对整体的径流变化模拟较好，说明考虑趋势变化和相邻数据之间关系的不确定性云模型对序列变化趋势的模拟效果很好。

图4 年径流量预测值与实测值的比较Fig.4 Comparison between measured and predicted annual runoff

6 结 论

本文在不确定性理论的基础上建立了云推理的预测模型，并以和田河同站实测年径流为例，对模型预测效果进行验证，结果令人满意。研究表明，考虑趋势变化和相邻数据之间关系的云模型可以识别数据中不确定性信息，提高模型的预测效率，避免将不必要的不确定性因素引入模型。通过与LS_SVM模型比较发现，云模型结构简单，方法简便，预测效果较好，相信有很好的应用前景。同时，云模型也存在需要进一步研究的方面：云模型在模拟极值时效果较差，而干旱地区的水文时间序列往往波动较大，因此云模型是否适用于干旱地区有待研究；本文在建模时只考虑了单因素情况，今后基于多因素的多维云模型建模将是研究的另一个方向。