复合决策粗糙建模与计算方法研究

汪琳娜，杨 新，杨习贝

1.四川工商学院 电子信息工程学院，成都 611745

2.Department of Computer Science,University of Regina,Regina,Saskatchewan,S4S 0A2

3.西南交通大学 信息科学与技术学院，成都 611756

4.江苏科技大学 计算机科学与工程学院，江苏 镇江 212003

1 引言

粗糙集理论是一种处理不确定性信息的粒计算模型之一，最早是由波兰数学家Pawlak[1]在集合论的基础上提出。该理论可以在缺少任何先验信息的基础上对数据进行有效处理，目前已广泛应用于医疗诊断、模式识别和人工智能等领域[2-5]。

在大数据时代数据类型通常呈现出多样化等特点。经典粗糙集通过二元等价关系对全体论域进行划分，运用严格的代数包含运算定义上近似集和下近似集，对不确定的知识进行刻画。但是在实际信息系统中，数据类型包含名义型、数值型、集值型、区间型和缺失型等，经典粗糙集不能有效处理以上类型的数据。为解决此问题，各种不同的二元关系被相继提出，如邻域关系[6]、偏序关系[7]、相容关系[8]、容差关系[9]等。针对各种单一类型数据，可以分别运用以上关系在粗糙集中对对象进行粒化处理，但是如何在粗糙集中同时对多种类型数据进行融合处理仍然是当前研究难点之一。目前有部分学者针对此问题开展了相关研究。Zhang等[10]通过严格的交运算针对等价关系、邻域关系、容差关系和特征关系定义了复合二元关系，进而提出了一种能够融合名义型、数值型、集值型和缺失型4种数据类型的复合粗糙集模型，给出了计算上下近似集的矩阵计算方法。Qian等[11]在多粒度空间下给出了融合多种关系的多粒度粗糙集模型，并进一步提出了悲观和乐观的多粒度决策粗糙集模型。Chen等[12]在概率粗糙集模型下给出了广义的复合概率粗糙集模型，并且研究了复杂数据下的最大分布约简问题。通过定义复合优势关系，罗川等[13]建立了基于复合有序二元关系的粗糙集模型。从以上研究可以发现，在粗糙集视角下处理复杂数据的关键是定义能够合理融合多种数据类型的复合关系。但是以上关于复杂数据融合的研究都没有考虑代价敏感的决策粗糙集方法。

Yao等[14]提出的决策粗糙集（Decision-theoretic Rough Set，DTRS）通过引入贝叶斯决策理论，在考虑期望决策风险代价最小的情况下给出了计算阈值的合理数学公式表达，为代价敏感的粗糙集决策提供了切实可行的方法。近年来，决策粗糙集以及由其导出的三支决策理论已经广泛地用来解决邮件过滤、石油投资、图像处理等问题[15-20]。本文以决策粗糙集模型为研究对象，采用多个二元关系处理各种类型的数据，然后在矩阵视角下探讨了不同二元关系的融合机制，并提出了基于量化复合关系的决策粗糙集模型及其矩阵计算方法，最后通过UCI数据集验证和分析了模型的有效性和稳定性。

2 决策粗糙集

定义1[1]一个具有单一数据类型的信息系统（简称为单类信息系统）可以定义为一个四元组S=(U,AT,V,f)：U是非空有限的对象集合；AT是非空有限的属性集合，中每个属性的类型相同；是值域，Va是对象在属性a下的所有可能取值；f:U×A→V是一个映射函数，使得∀a∈AT,x∈U,f(x,a)∈Va。

定义2[1]设S是一个单类信息系统。，EA是论域U上由A诱导出的一个等价关系，定义为：

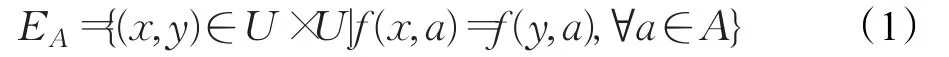
根据式（1），论域U在等价关系EA下被分成若干等价类，记为，其中[x]EA称为包含对象x的等价类。∀X⊆U，经典粗糙集的上下近似集可以定义为：

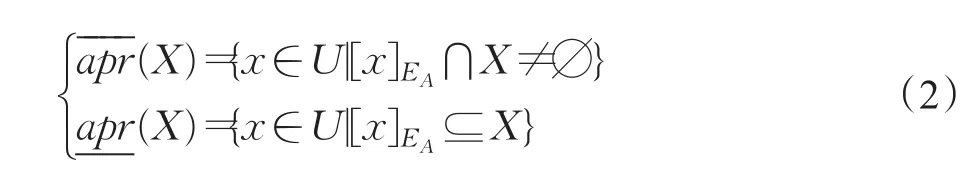
针对经典粗糙集模型缺乏容错能力的问题，引入概率近似空间可以得到概率粗糙集模型。

定义3[14]设S是一个单类信息系统。给定一对阈值对 (α,β)，其中 0≤β＜α≤1，则概率粗糙集模型的上下近似集可以定义为：

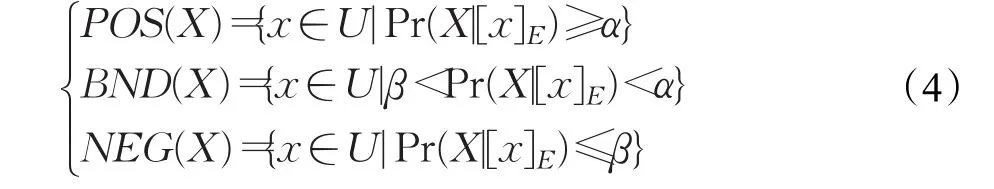
下面以二分类问题为例。在单类信息系统S中，可以用具有2个状态的集合Ω={X,¬X}和3个行动的集合A={aP,aB,aN}来描述贝叶斯决策过程。其中状态集中X和¬X互补，行动集中aP、aB、aN分别表示将对象分类到正域、边界域和负域的决策动作。给定一个损失函数矩阵如下：

其中，λPP,λBP,λNP分别表示当状态为X时采取行动aP、aB、aN下的损失，λPN,λBN,λNN分别表示当状态为¬X时采取行动aP、aB、aN下的损失。因此可以给出分别采取行动aP、aB、aN下的期望损失为：

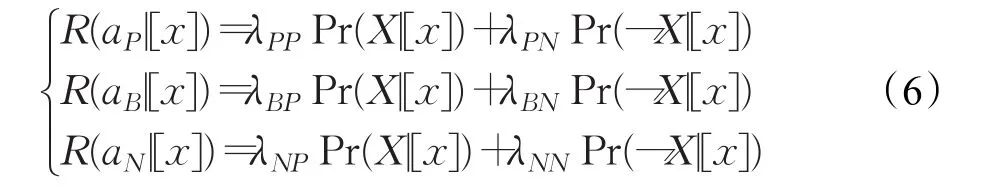
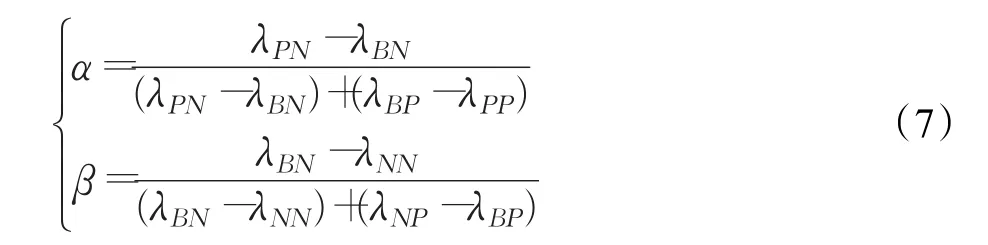
根据贝叶斯决策准则，我们会选择期望损失最小的行动集作为最佳的行动方案。通过推导（详细过程可参见文献[14]），可以得到关于阈值对 (α,β)的具体计算公式如下：

3 复合决策粗糙集模型

经典决策粗糙集模型只能运用等价关系处理名义型数据的分类和决策问题。在本章中，讨论了多种类型共存的复杂数据的三种融合策略，并提出了一种基于量化复合关系的决策粗糙集扩展模型，探讨针对复杂数据的代价敏感决策问题。

例1表1给出了一个复合信息系统CS示例，其中论域，属性其中AT′前4个属性子集的数据类型分别为名义型、数值型、区间型、集值型，第5个属性子集为名义型的决策属性。

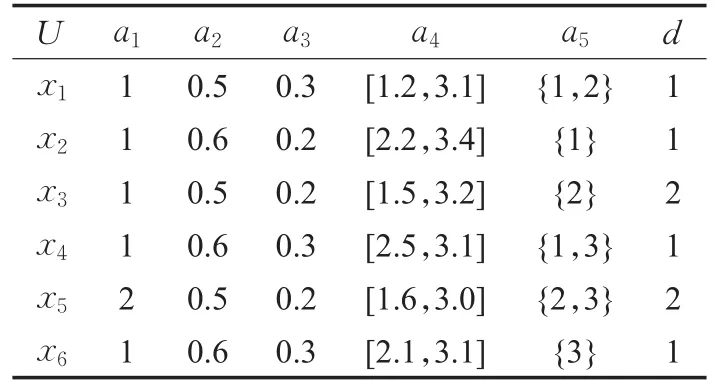
表1 复合信息系统

定义5[10]设R是一个二元关系，则可以给出U上关于R的关系矩阵，其中：

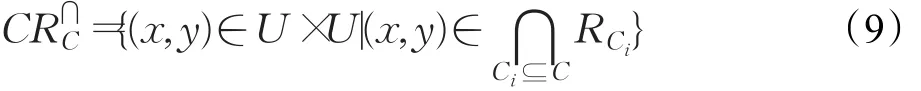
其中RCi表示同一数据类型在属性集Ci上的二元关系，上式也可简记为：

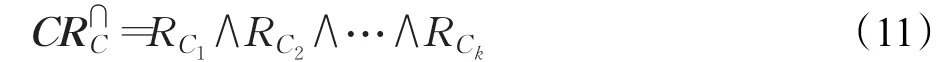
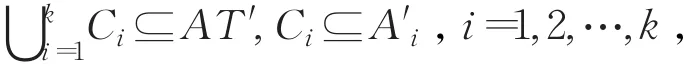
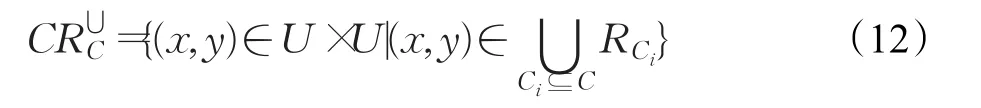
其中RCi表示同一数据类型在属性集Ci上的二元关系，上式也可简记为：

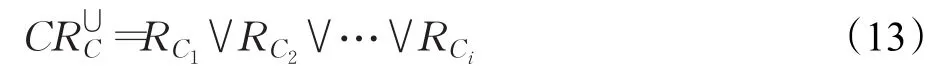
在复合信息系统下，以上给出了关于多个二元关系的交-复合关系和并-复合关系。交-复合关系比较严格，要求两个对象要满足每一个二元关系，容易造成粒化过细；并-复合关系相对宽松，只要求两个对象满足其中任一个二元关系，但容易造成粒化过粗。因此为了得到可以量化的复合关系，给出以下定义。

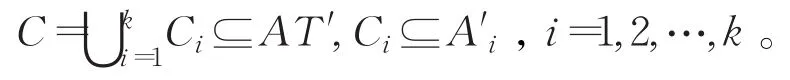
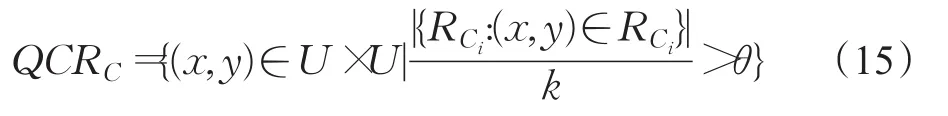
其中k表示二元关系的数量（每一个数据类型对应一个二元关系）表示两个对象间满足二元关系的总数量。此时关于QCRC的复合关系矩阵MQRCC=的元素可以表示为：

由上式可知，量化复合关系满足自反性，不一定满足对称性和传递性。

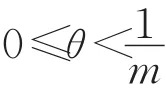
由定理1可知，量化复合关系是并-复合关系和交-复合关系的推广形式。下面基于量化复合关系给出复合决策粗糙集的定义。

定义9给定一个复合信息系统CS，则复合决策粗糙集的上下近似集可以定义为：

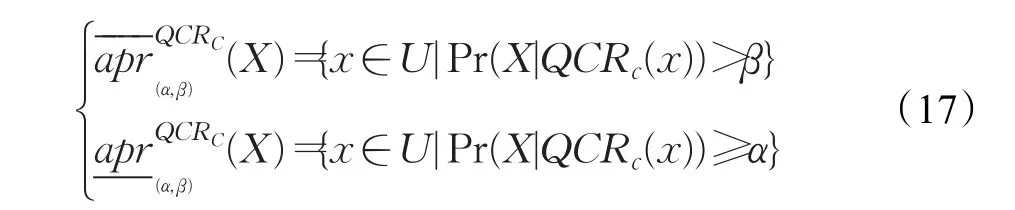
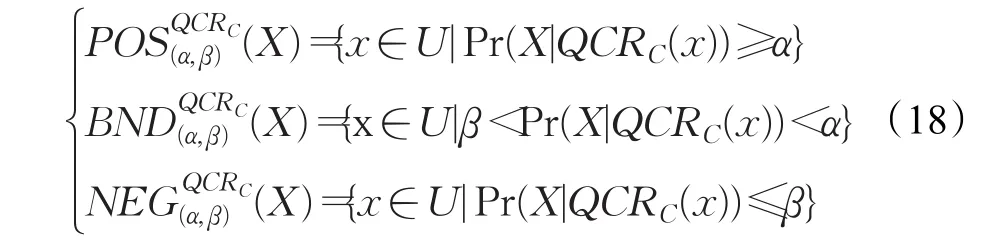
下面给出复合决策粗糙集的一些性质。

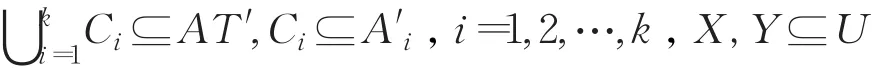
4 近似集的矩阵计算

通过对多个二元关系的量化融合处理，可以利用阈值θ有效控制数据融合的效果，并运用复合决策粗糙集对复合信息系统进行代价敏感分类和决策。下面采用布尔矩阵分析二元关系融合处理的过程，并给出了一种新的复合决策粗糙近似集的矩阵直观计算方法。

定义10[10]设U={x1,x2,…,xn}是一个非空有限的对象集合，X是U的任意一个非空子集，即，则X可以表示为布尔矩阵如下：

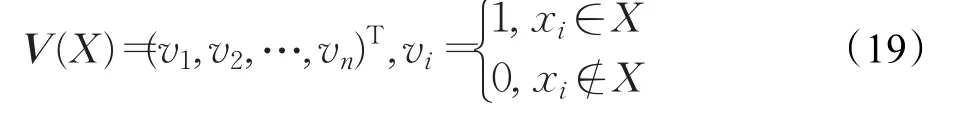
其中V(X)为X在U上的特征矩阵，T为矩阵的转置运算。

例2在表1中，给定一个复合信息系统CS，其中论域U={x1,x2,x3,x4,x5,x6}。假设X={x1,x2,x4, }x6，则X在U上的特征矩阵为V(x)=[1,1,0,1,0,1]T。

表1中存在名义型、数值型、区间型、集值型数据，因此可以分别运用等价关系、邻域关系、偏序关系、相容关系计算不同类型属性集合下的二元关系。

（1）如果属性集Ci是名义型数据，则采用定义2中的等价关系计算关系矩阵。

（2）如果属性集Ci是数值型数据，则采用欧氏距离空间下的邻域关系[6]计算关系矩阵，可以表达为：

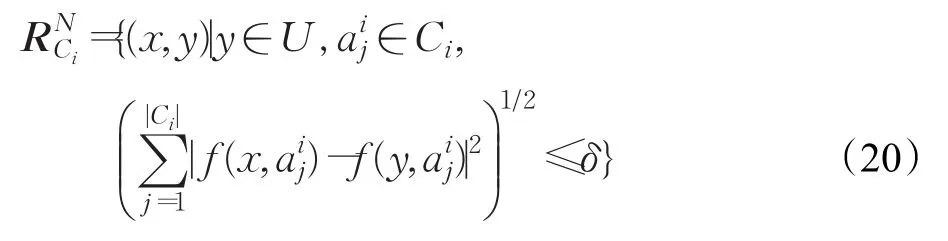
（3）如果属性集Ci是区间型数据，则采用偏序关系[7]计算关系矩阵，可以表达为：

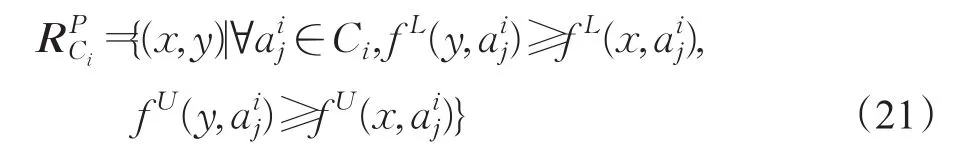
（4）如果属性集Ci是集值型数据，则采用相容关系[8]计算关系矩阵，可以表达为：

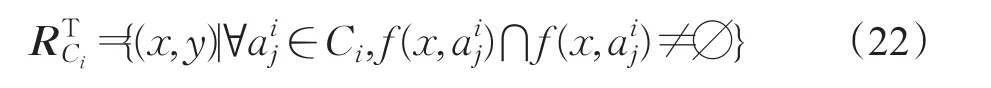
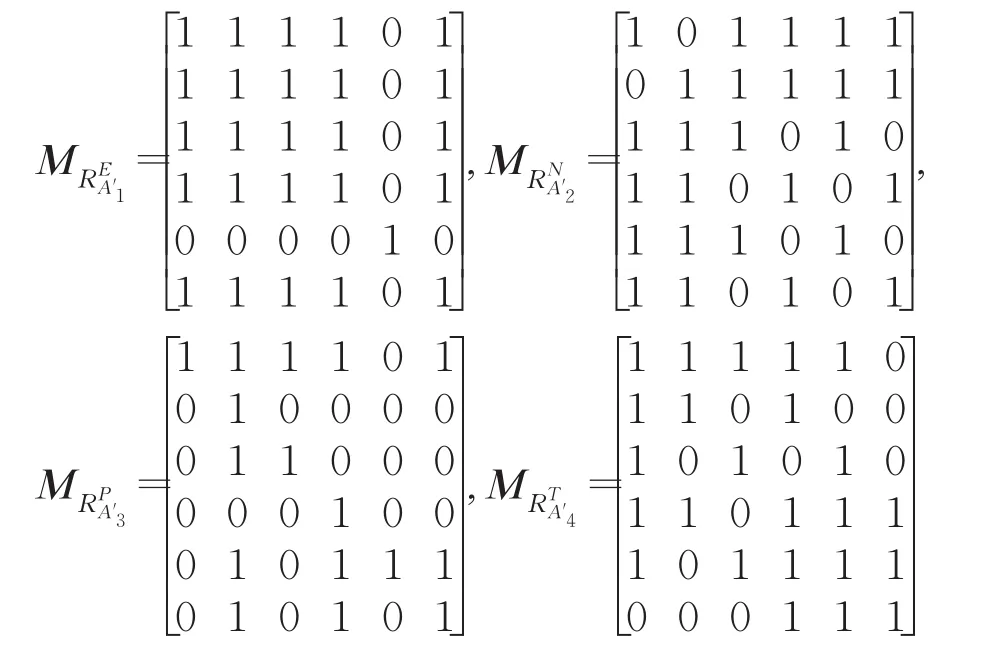
例3假设邻域关系中的δ=0.1，根据以上4种二元关系，可以对表1中的数据分别计算得到各自的关系矩阵如下：

由以上4个关系矩阵可以得到交-复合关系CR⋂C下的复合关系矩阵为：

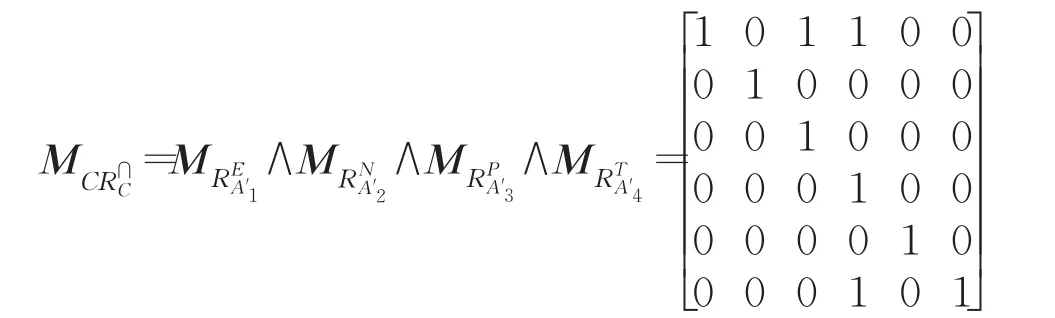
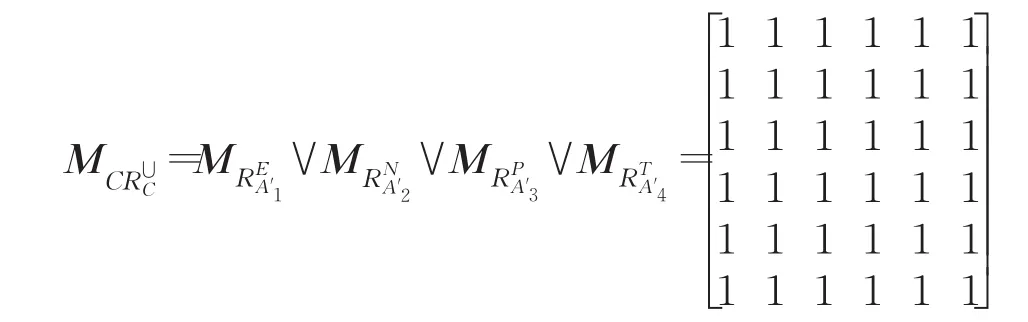
假设量化阈值θ=0.7，则量化复合关系QCRC下的复合关系矩阵为：

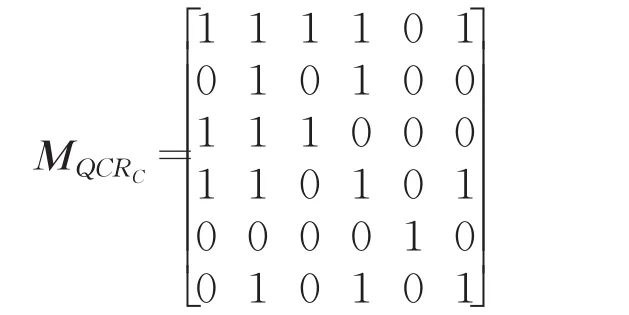
文献[10]和[13]中均是运用特征矩阵、关系矩阵及其诱导矩阵三者的数量积运算和截矩阵计算粗糙集的上下近似集。与以上文献不同，下面给出一个更加简洁的矩阵计算近似集的方法。根据文献[21]，首先给出复合决策粗糙集的一个等价定义。

定义12给定一个复合信息系统CS，则复合决策粗糙集的上下近似集还可以定义为：

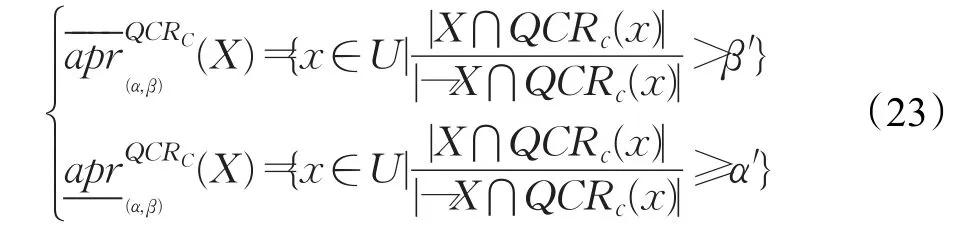
定义13假设一个矩阵Mn×1，则两个截矩阵可以表示为：

根据以上定义的特征矩阵、复合关系矩阵和截矩阵，下面在不计算诱导矩阵的前提下给出更加直观的矩阵计算复合决策粗糙近似集的方法。

定义14给定一个复合信息系统CS，X是U的任意一个非空子集，即X⊂U，V(X)为X在U上的特征矩阵。QCRC是量化复合关系，由其诱导出的复合关系矩阵为MQCRC，M↓和M↑为两个截矩阵，则基于量化复合关系的复合决策粗糙集上下近似集的矩阵计算方法可定义为：

定义14给出了基于布尔代数构造复合决策粗糙近似集的方法，计算过程简单直观，为决策粗糙集中处理和运算复杂大数据提供了一个新的方法。具体计算过程如下所示。

算法1矩阵计算复合决策粗糙集的上下近似集

输出：上下近似集的特征矩阵。

步骤1计算概念X的特征矩阵V(X)；

步骤2按照不同数据类型根据不同的二元关系分别计算他们的关系矩阵

步骤3计算量化复合关系矩阵MQCRC；

步骤4计算交矩阵和非交矩阵V(¬X)；

步骤5根据截矩阵计算上下近似集的特征矩阵。

由以上分析可以得出，算法时间花费主要集中在构建关系矩阵。

例4对表1中的复合信息系统CS，根据例1～3的结果和定义14，假设代价矩阵为：

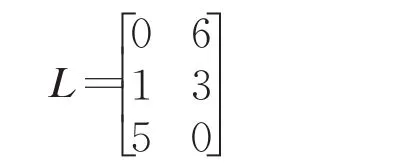
则根据定义12可以计算出新阈值对α′=3，β′=0.75。可以用矩阵的方法得出复合决策粗糙集模型的下近似集为：

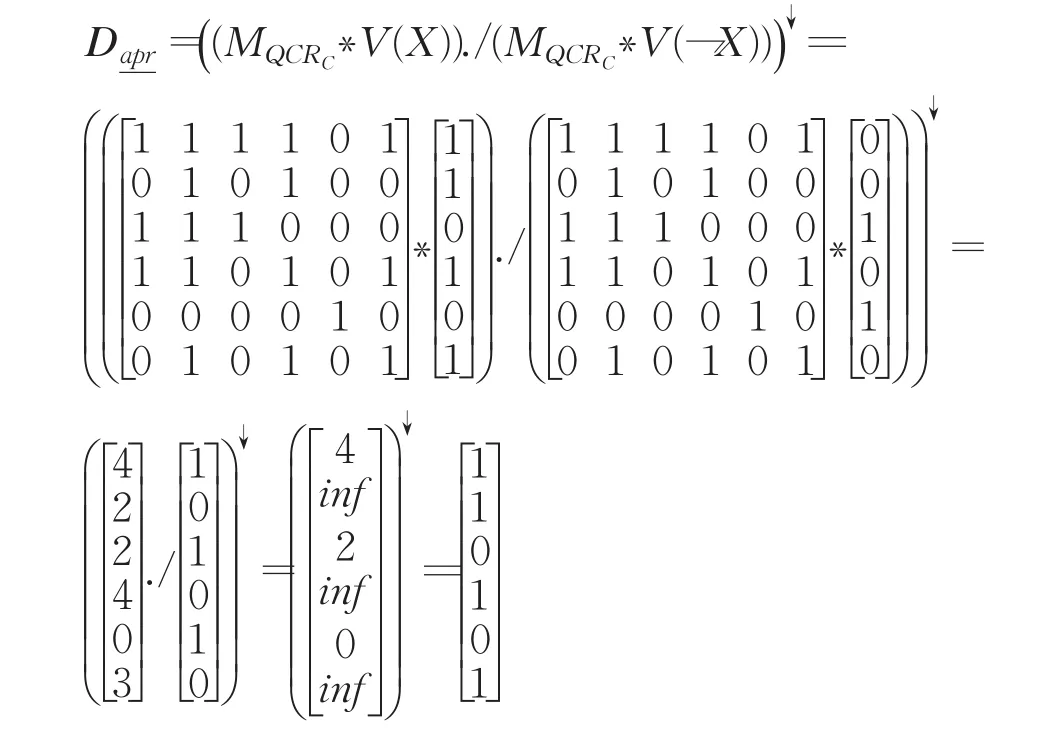
同理可得复合决策粗糙集模型的上近似集为：

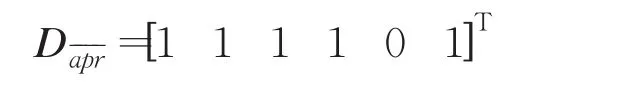
根据以上矩阵计算结果，可以得到复合决策粗糙集模型的上下近似集为：

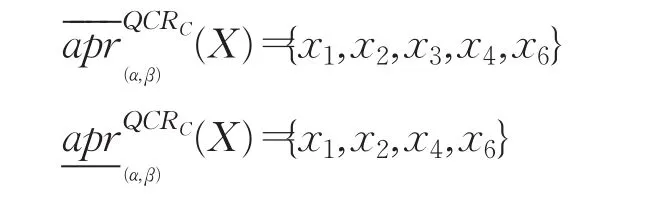
5 实验分析

为了分析和验证本文提出的复合决策粗糙集模型的有效性和矩阵方法的稳定性，从UCI数据集中挑选了2组数值型数据集，并通过机器自动生成了2组多类型共存数据集，具体数据信息见表2所示。

表2 数据集信息

所有实验都在PC电脑上运行，其配置为Intel®Core™i5-4210U CPU@1.70 GHz，12 GB内存，Windows10 操作系统，Matlab2016a实验平台。在实验中挑选了10组邻域阈值参数δ，分别为0.05，0.1，…，0.5，并设置量化阈值θ=0.7来分析矩阵计算所用时间组成。具体实验效果如图1所示。

图1中（a）、（b）、（c）、（d）分别描述4个数据集在复合决策粗糙集中近似集的矩阵计算时间组成。在图1（a）和（b）中，可以观察到在不同邻域下的矩阵计算时间相差不大，而且关系矩阵计算时间占总计算时间比例都超过95%。在图（c）和（d）中，给出了4种不同类型数据的关系矩阵和近似集的计算时间曲线。通过比较发现，4个关系矩阵花费时间从高到低分别是区间型、集值型、数值型和名义型。在不同邻域阈值下，近似集的总计算时间没有太大变化，说明矩阵算法在时间消耗方面比较稳定。

6 结束语

针对经典决策粗糙集不能有效处理复合信息系统中的分类和决策问题，本文通过深入研究多种二元关系的融合机制，提出了基于量化复合关系的决策粗糙集模型，并给出了一种新的矩阵计算上下近似集的方法，通过实例和UCI数据集分析了模型和算法的有效性和稳定性。在以上研究中，数据类型没有涉及音频、视频、文本等，下一步工作，计划在多模态复合信息系统下运用决策粗糙集开展代价敏感决策研究。

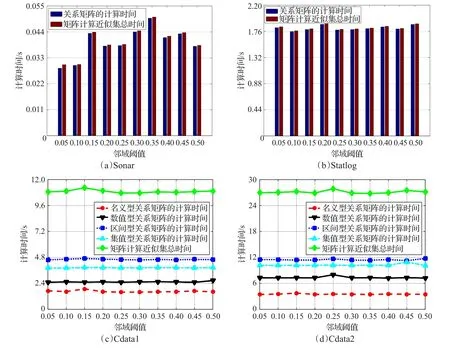
图1 近似集的矩阵计算时间分析