产业集聚与区域经济增长的空间溢出效应研究——基于中国省级制造业空间杜宾模型

唐建荣，房俞晓，张鑫和，唐雨辰

(1.江南大学 商学院，江苏 无锡 214122； 2.利物浦大学 管理学院，英国 利物浦 L693BX)

一、引言

产业集聚是经济活动在空间集聚的重要地理特征，其实质是资本要素在空间范围内合理流动并逐渐归集的过程。长久以来，制造业被普遍认为是国民经济发展的根基和动力，而制造业的集聚水平和发展程度对于衡量一个区域的综合竞争力及现代化程度至关重要。近十年来，中国制造业不断繁荣发展，整体规模不断扩大，2016年中国规模以上制造业企业实现利润62 398亿元，同比增长12.3%，制造业已经成为促进中国经济增长的重要源动力。“十三五”时期，中国正式印发了《中国制造2025》，该纲要明确了制造业国民经济的主体地位，并提出要提高产业集聚的层次和质量，培育一批国际化的特色制造业集群，以加快制造业转型升级的步伐，推动中国经济健康协调发展。然而，中国制造业区域发展差异较大，制造业集聚呈现出明显的中心-边缘特征，东部沿海地区制造业集聚明显，且中心度自东向西、由沿海至内陆逐渐降低。因此，研究制造业集聚与中国区域经济增长的内在影响机制及其存在的空间溢出效应，对中国未来制造业空间布局的调整优化和促进区域经济发展，具有重要意义。

Marshall是研究工业集聚现象的新古典经济学派先驱，他从外部规模经济的角度阐述了“产业区”的形成，产业集聚主要通过共享劳动力市场、知识溢出、节省运输成本促进效率提升，为后人的研究奠定了思想基础[1]。Hoover提出了产业集聚的最佳规模理论，认为产业集聚与经济增长存在自我强化机制，产业集聚产生的外部性会吸引同类经济体加入集聚区，使集聚体进一步强化，从而促进区域经济增长[2]。20世纪90年代以来，以Krugman、Fujita等人为代表的新经济地理学派，在规模报酬递增和不完全竞争理论的基础上，将空间区位因素纳入一般均衡的分析框架中，实现了主流经济学向地理空间的扩展。产业空间集聚能否提升区域竞争力进而促进经济增长，备受国内外学者关注。Martin等人构建了经济增长和产业集聚自我相互强化的过程模型，证实产业集聚能够通过交易成本的外部性降低创新成本，从而促进经济发展，同时经济增长又推动了以地区专业化分工为基础的产业集群进一步扩张[3]；Geppert等人利用西德1980—2000年20年的数据，验证了产业的地理集中与经济增长呈正相关关系[4]；陈建军等人通过VECM和协整分析对1978—2005年长三角区域进行实证研究，结果表明产业集聚能够使集聚区内人民生活质量得到提高和推动区域技术发展，并使经济实现进一步增长[5]；潘文卿等人采用HHI指数作为产业集聚测算指标，利用动态面板两阶段系统GMM估计方法，测算了2001—2007年中国制造业产业集聚与经济增长的关系，结果显示两者存在显著正相关[6]；李秋雨等人构建了中国旅游产业发展与经济增长之间的空间计量模型，结果表明国内旅游和入境旅游业存在空间集聚现象，且对经济增长有着显著的正向影响[7]。

然而，并不是所有学者都认为产业集聚会对经济增长产生积极影响，还有一些学者得出了二者存在显著的负相关或无相关关系的结论。比如谢波基于1990—2010年中国中、西、东部地区的省际面板数据进行分析，结果表明资源产业集聚对经济增长产生负向作用[8]；Ercole等人采用区位熵指标测算了印度尼西亚2000—2009年五位数制造业的集聚水平，并得出了专业化集聚与制造业增长成反比的结论[9]。此外，还有部分学者认为两者之间并不是简单的线性关系，而是呈现倒U型，即产业集聚一开始对经济增长产生积极作用，待达到一定程度后会出现负相关。

通过文献梳理发现，从研究视角上看：现有研究主要研究了产业集聚与经济增长之间的线性或非线性关系，虽然现有研究已考虑了地区间差异影响，但目前大部分研究都将区域视为一个独立个体进行分析，忽略了区域间的空间联系，鲜有研究考虑到产业集聚的地理位置与经济增长是否有关；从研究方法上看：近年来关于制造业集聚与经济增长的研究主要采用的是 OLS 回归、动态面板数据一阶差分广义矩方法、系统动态 GMM 法等，鲜少考虑到空间效应的存在，而空间计量方法的提出为空间效应的研究提供了可能。Anselin提出区域地理空间单元上的某种经济特征与临近地区经济特征是相关的[10]。目前，中国正处于制造业转型的新时期，与以往的研究相比，本文主要基于Anselin的空间计量经济学理论，从空间溢出效应的角度出发，尝试将地理因素纳入到制造业集聚与区域经济增长的关系中，同时添加各生产要素作为控制变量，通过构建空间计量模型，揭示中国制造业集聚与区域增长的逻辑关系及空间溢出效应，从而避免普通面板模型不涉及空间相关性的缺陷，对于中国未来制造业空间布局的调整优化及区域经济水平的提升，都将具有一定的现实意义。

二、制造业集聚与经济增长逻辑关系测定

笔者认为，制造业集聚促进区域经济增长的内在机理在于企业共享因制造业集聚而形成的规模经济效益、成本节减效益和资源共享效益，从而促进区域专业化分工、提高集聚区内生产效率、优化地区资源配置，使得区域经济得到进一步发展。一方面，由于产业集聚存在自我强化机制，会进一步吸引各类企业在该地区集聚，形成愈加明显的经济效益；另一方面，由于空间地理位置的邻近性，区域间资本要素自由流动，集聚区会产生空间溢出效应，通过区域集聚的溢出效应，知识、技术、人才、交通等资源向邻近省域辐射传播，从而带动邻近省域的经济发展。同时，制造业集聚还通过城市化效应，加快了集聚区内城市化进程，促进产业结构优化升级，对区域经济产生积极的外部效应。因此，本文首先通过探索性空间数据分析方法(ESDA)探索中国省域经济增长水平的空间自相关规律，继而通过构建适宜的空间计量模型，以揭示省域制造业集聚与经济增长的内在逻辑关系。

(一)探索性空间数据分析(ESDA)

探索性空间数据分析(ESDA)通常被用来验证空间数据是否存在自相关性，而空间自相关实质上展现的是某一要素在不同地理单位的空间集聚特征，用于阐明研究对象在空间分布中存在的集聚和相关性程度[11]。本文利用全局Moran'sI统计量测算中国省域经济发展的全局空间自相关系数，采用局部Moran指数、散点图及LISA集聚图直观地展示其局部空间自相关性。

1.全局空间自相关。全局Moran'sI统计量指空间相邻区域单元的属性相近度。利用Moran'sI验证中国省域经济增长全局空间相关性的存在，该指数被定义为：

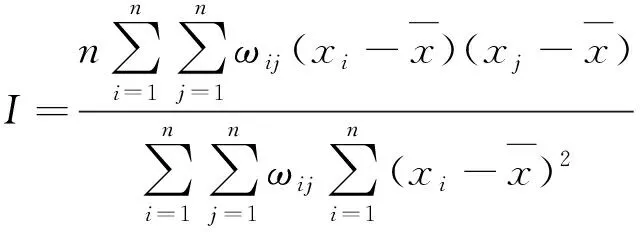
(1)

其中n为区域数量，xi和xj分别为地区i和j的样本观察值，ωij是标准化的空间权值矩阵。全局Moran'sI指数的取值区间一般为[-1,1]，大于0代表正相关，小于0则表示负相关。

2.局部空间自相关。全局Moran'sI统计量仅描绘省域经济增长的全局相关性，因此引进局部Moran指数并绘制局部Moran散点图，进一步度量每个省与邻接省域间经济增长的关联性与异质性。局部Moran指数被定义为：

(2)

其中Ii为正，表明该省与邻省的属性相似(“高-高”或“低-低”集聚)；Ii为负，则说明该省与邻省的属性不相似，存在空间异质性(“高-低”或“低-高”集聚)。

(二)空间计量模型

由于空间样本观察值存在一定的相关性，与传统计量经济学中样本观察值不相关的假设基础相悖，而传统计量方法会导致样本信息失真及结果有偏。通过ESDA方法分析确定中国省域经济增长存在空间相关性，纳入地理因素并建立合适的空间计量模型，可以探讨中国制造业集聚与经济增长的空间溢出效应。

空间计量模型是对纳入不同空间交互效应的普通回归模型的拓展，主要包含以下三类：

1.空间滞后模型(Spatial Lag Model，SLM)

(3)

其中i为截面维度样本，t为时间维度数据；yit为因变量样本观察值；δ为空间自回归系数；ωij为空间权重矩阵所含元素，表示区域i和j的邻近关系；xit为k维自变量样本观察值；β为k维回归系数列向量；μi为个体固定效应；εit为随机误差项。此模型包含了因变量之间的内生交互项，侧重揭示一个主体的因变量的取值与相邻主体的因变量取值有关。

2.空间误差模型(Spatial Error Model，SEM)

SEM模型包含了误差项间的交互效应，侧重揭示被忽略因变量的决定因素是具有空间相关性的，或者不可观测的冲击服从空间交互的形式，其基本表达式为：

yit=xitβ+μi+uit

(4)

(5)

式(4)(5)中uit为空间误差自相关，λ为自相关系数。

3.空间杜宾模型(Spatial Durbin Model，SDM)

SDM模型同时包含了内生及外生交互效应，除了包含SLM模型的内生交互项外，还侧重揭示了特定主体的因变量与相邻主体的独立自变量取值有关的外生交互效应。SDM模型为：

(6)

其中γ为k维回归系数列向量。

制造业集聚不仅会对本区域经济活动的空间分布产生影响，还可能会对相邻省域的经济增长产生重要的空间溢出效应。空间计量经济学的提出为空间溢出效应的研究提供了可能，因此本文将根据研究内容设定合适的空间计量模型，深入揭示不同时间和空间视阈下制造业集聚对区域经济增长的影响机理。

三、变量选取与模型设定

通过文献梳理，结合前人研究，本文以柯布-道格拉斯生产函数为基础，选择合适的数据表征变量，并将制造业集聚变量及与经济增长相关的5类控制变量纳入一般生产函数，建立空间计量模型并对其进行实证研究。

(一)变量选取与数据来源

国民经济行业分类标准自2012年开始发生变化，为保证数据的连续性和完整性，本文选取了2012—2015年期间全国31个省份(不包括港、澳、台及南海诸岛)的面板数据进行实证研究。数据来自2012—2015年《中国统计年鉴》、《中国工业统计年鉴》、《中国劳动统计年鉴》、《中国科技统计年鉴》及各省统计年鉴。

1.被解释变量。为消除省域规模因素影响和增加数据可比性，本文以2005年为基期，利用GDP平减指数得到各地区人均实际生产总值表征中国经济增长状况。

利用ArcGIS软件，以2015年中国31个省份人均实际GDP为衡量指标，绘制中国省域经济增长空间分布六分位图(见图1)，颜色愈深表明该省经济发展水平愈高。由此可以看出，中国省域经济增长水平存在比较明显的区域差异，大致呈现从东部地区向中西部地区逐渐降低的趋势。同时，省域与邻近地区颜色相近，表明中国省域经济增长水平大致相近，呈现比较明显的空间集聚分布特征。

图1 2015年中国人均实际GDP六分位图

2.核心解释变量。区域经济的集聚与扩散理论认为，在集聚效应促进经济增长的同时，通过扩散效应也可以推动周边地区经济的发展。自20世纪90年代以来，产业集聚理论开始快速发展，关于产业集聚水平的衡量指标也有了长足的进步，已愈加符合产业集聚的真实情况。在产业集聚的量化研究中，目前的衡量指标主要有行业集中度、区位熵、HHI指数、EG指数等，而运用区位熵指标可以消除区域规模差异，分析区域内产业的集聚倾向。本文采用区位熵指标测算制造业集聚情况，具体测算公式为：

(7)

表1表明：2012—2015年间中国制造业区位熵均值超过1的地区有12个，说明这12个地区存在制造业集聚；其中区位熵始终超过1的有山东、江苏、河南、广东、江西、安徽、天津、浙江、吉林 9个地区，表明这9个地区与全国相比具有比较优势，产业集聚程度较高。显然，中国制造业集聚存在比较明显的区域差异，大致呈现从东部地区向中西部地区逐渐降低的趋势，这与中国的经济发展水平的空间分布大致上是相同的。另外，由于劳动力、土地等要素成本的增加，部分经济发达地区制造产业开始内迁或外移，导致制造业集聚呈现缓慢发展甚至下降趋势，如上海、浙江的集聚优势减弱，而江西、河南等中部地区凭借劳动力资源、价格等优势承接了东部地区的制造业转移，集聚程度得到了加强。

表1 中国31个省份制造业区位熵指数表

注：根据式(7)，利用2012—2015年《中国工业统计年鉴》、《中国统计年鉴》及各省统计年鉴数据整理计算所得。

3.控制变量。选取人力资本投入、固定资产投资、技术创新、基础设施建设、城市化等5个要素作为控制变量，以更加全面地揭示中国省域经济增长效应。

(1)人力资本投入：根据Lucas模型，人力资本形成的最佳实现途径为教育。因此，本文参考刘军的做法，利用平均受教育年限表征人力资本投入情况，其中将未上过学、小学、初中、高中、专科、本科、研究生及以上的受教育年限分别设置为0、6、9、12、15、16、19年，用上述7种学历层次就业人员所占比例与相应受教育年限乘积之和来度量各地区人力资本投入。

(2)固定资产投资：固定资产投资作为促进经济全面发展的“三驾马车”之一，无疑是实现经济增长的重要源泉。本文以2005年为基期，利用各地区固定资产投资价格平减指数得到各地区全社会实际人均固定资产投资，并据此度量各省区固定资产投资，其中西藏无此价格指数，因此用商品零售价格指数(RPI)代替。

(3)技术创新：技术创新是中国发展的核心战略，有利于提高生产效率、降低成本，为经济增长提供巨大动力，而研发投入又是促进技术创新发展的源泉，因此采用R&D人员全时当量代表各地区创新程度。

(4)基础设施建设：经济发展离不开基础设施建设的推动，公共交通网络的通达性对物质资本的运输、促进生产要素的流动具有重要意义，因此采用铁路和公路营业里程之和比各省面积表示各地区基础设施建设状况。

(5)城市化：城市化打破了城乡壁垒，提升了资源聚集能力，是实现现代化的必经之路，也是促进区域协调发展的有力支撑，故采用分地区年末城镇人口比重代表城市化水平。

(二)制造业集聚与区域经济增长

以柯布—道格拉斯生产函数为基础估计集聚的经济效应，是目前研究中较为常用的方法。为了研究制造业集聚对经济增长的作用，本文引入制造业集聚变量和其他能够影响经济增长的控制变量，将原有C-D生产函数改进为：

(8)

其中Yit表示被解释变量经济增长，即为t时期i区域的人均实际生产总值；Ait为综合技术水平；Qit为核心解释变量制造业集聚，即为t时期i区域的制造业区位熵；ψ为制造业集聚对经济增长的影响系数；Lit、Kit、Fit、Zit、Hit为控制变量，分别表示t时期i区域的人力资本、固定资产、技术创新、基础设施、城市化投入量；α、β、φ、σ、υ为各控制要素对经济增长的影响系数。

为消除改进后生产函数中存在的数据异方差性，将式(8)取对数形式，构建制造业集聚对经济增长影响的普通面板模型为：

lnYit=lnAit+αlnLit+βlnKit+ψlnQit+

φlnFit+σlnZit+υlnHit+εit

(9)

以改进后的普通面板模型为起点纳入空间地理因素，由此分别构建相应的空间计量模型为：

SLM模型

φlnFit+σlnZit+υlnHit+μi+εit

(10)

SEM模型

lnYit=αlnLit+βlnKit+ψlnQit+φlnFit+

σlnZit+υlnHit+μi+uit

(11)

(12)

SDM模型

(13)

上述3种模型为涉及不同交互效应的制造业集聚与经济增长的空间计量模型。SLM模型(10)侧重研究本省域产业集聚与相邻省域经济增长对本省域经济增长的影响；SEM模型(11)、(12)则主要探讨了本省域产业集聚、被忽略掉的扰动误差项对本省经济增长的影响；而SDM模型(13)不仅揭示了相邻省域经济增长的空间溢出效应，还研究了相邻省域产业集聚对本省经济增长的作用，符号含义与式(3)～(6)相同。

四、实证分析与估计结果

根据空间计量经济学原理，首先通过探索性空间数据分析(ESDA)检验中国31个省域经济增长的空间依赖性。

(一)区域经济增长空间相关性分析

1.全局空间自相关分析。依据一阶Rook原则构建空间权重矩阵，利用GeoDa软件得到中国31个省份经济增长水平的全局Moran'sI指数及显著性检验结果，见表2。

表2 中国31个省份经济增长全局Moran's I指数表

由表2可知：2012—2015年中国经济增长水平的全局Moran'sI指数均在0.4以上，最高年份达到了0.460；同时，所有年份的Moran'sI指数的P值皆小于0.01，全部通过了显著性检验，这说明中国经济增长水平存有非常明显的空间正自相关性，即存在空间集聚效应，临近地区的经济发展水平呈现出一定的相似性。

2.局部空间自相关分析。为更深入地对中国经济增长的空间相关模式进行分析，以2015年为例，绘制中国经济增长的局部Moran散点图，见图2。

图2 2015年中国经济增长局部Moran散点图

由图2可知：中国31个省份在第一第三象限分布较多，即中国经济增长的空间相关模式以“高-高”和“低-低”集聚为主；其中处于“高-高”象限的省份有7个，而处在“低-低”象限的省份有15个，共占全国总量的71%，说明中国经济增长水平在空间存在非常明显的正相关性。

由于Moran散点图包含了所有研究区域，并不能判断各省份集聚区是否能够通过显著性检验，因此利用ArcGIS软件绘制2015年中国经济增长的LISA集聚图，进一步探讨具体省域经济增长对邻近地区的影响程度，见图3。

图3中有图形填充的地区表明省域经济增长空间关系显著，其中“高-高”区域表明该省域与邻省的经济增长水平都比较高；“低-低”区域表明该省与邻近省域的经济增长水平都比较低；“低-高”区域表明该省经济增长水平较低，而其邻省较高；“高-低”区域表明本省经济增长水平较高，但其邻近省域较低。

图3 2015年中国经济增长LISA集聚图

由图3可以看出：位于“高-高”集聚区的省份分别为江苏、上海；“低-低”集聚区主要分布在西部地区，包括：新疆、西藏、云南、贵州、青海、四川；另外，河北处于“低-高”集聚区，因为相比北京、天津及上海等周边地区，河北的经济增长水平较低。总体而言，中国经济增长的空间集聚特征明显，具有显著的自相关性，其集聚模式呈现出梯度发展的趋势，东部区域经济增长水平较高，西部经济增长则相对较低。

(二)空间计量模型的选择

探索性空间数据分析(ESDA)结果表明，中国各省的经济增长存在正向空间自相关性，由此可以根据相应的判定准则选择合适的空间计量模型，以探究制造业集聚与中国经济增长水平的溢出效应。

1.固定效应与随机效应。根据非观测效应的不同，面板数据模型可以分为两大类，即固定和随机效应；其中固定效应又可以分为时期固定、空间固定以及时期空间双固定效应，利用Hausman检验可以对固定效应和随机效应进行选择。一般来说，当样本回归分析限定于某些特定的个体时，应选择固定效应模型。因此，利用Matlab2016b软件，首先对未纳入空间因素的普通面板模型进行混合OLS回归估计及LR检验，判断其存在何种交互效应，详细结果见表3。

由表3可知：Hausman检验值为32.861，通过1%的显著性检验，即拒绝随机效应模型，再次证明使用固定效应更佳；同时，LR时期固定和LR空间固定效应检验结果皆通过了1%显著性检验，拒绝了时期固定和空间固定效应的混合非显著性的原假设，因此可以将模型扩展为时期空间双固定模型[12]。通过双固定模型估计结果可以看出，制造业集聚、固定资产投入、城市化对中国经济增长水平的影响系数均为正数，且通过了显著性检验。然而，由于中国经济增长水平存在明显的空间相关性，因此未纳入空间效应的普通回归模型的估计系数会产生偏差。

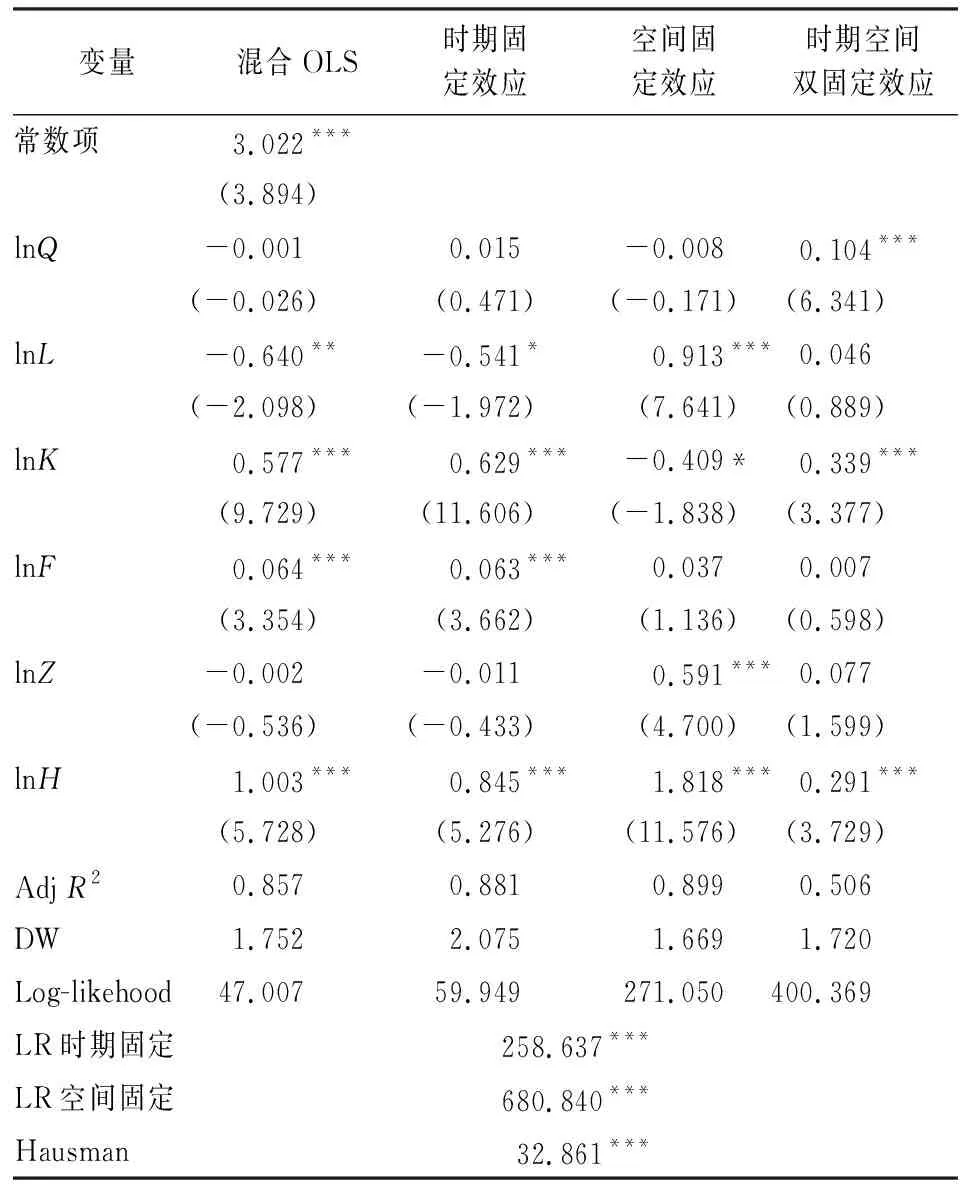
表3 普通面板模型OLS估计及LR检验结果表

注：*、**、***分别代表0.1、0.05、0.01的显著性水平；括号内为t统计值。

2.空间滞后模型与误差模型。根据Anselin提出的判别准则，可以判断SLM与SEM模型的选择，即假若LMlag比LMerror在统计上更加显著，且R-LMlag比R-LMerror在统计上更加显著，则选择SLM模型，反之选择SEM模型[13]；利用时期空间双固定效应下的普通面板OLS估计得到的残差序列进行LM检验，得到的LMlag值为8.512、R-LMlag值为17.887，均通过了1%显著性检验；而LMerror值为0.402，未通过显著性检验，因此应选择双固定效应下的SLM模型(10)要比SEM模型(11)(12)更为合适。

3.空间杜宾模型。由于LM检验并没有考虑到SDM模型的适用性，因此可以根据Burridge提出的判别准则，判断SDM模型是否可以简化为SLM或SEM模型，即可以通过Wald检验和LR检验来检验原假设H0：θ=0和H0：θ+δβ=0，如若检验结果同时拒绝了这两个原假设，则SDM模型能够最好地拟合数据；若拒绝了前一个假设且R-LMlag值显著，则SDM能够简化为SLM模型；同理，若拒绝了后一个假设且R-LMerror值显著，则SDM能够简化为SEM模型[14]。因此，利用Matlab2016b软件，得到双固定效应下SDM模型中Wald和LR检验的检验值，据此判断SDM模型是否可以简化，详细结果见表4。

表4 双固定SDM模型的Wald和LR检验结果表

注：*、**、***分别代表0.1、0.05、0.01的显著性水平。

由表4可知，无论是SLM模型还是SEM模型的Wald值和LR值，都通过了1%显著性检验，拒绝了原假设，即SDM模型不能简化。利用极大似然法(ML)估计不同交互效应下的SDM模型，具体结果见表5。

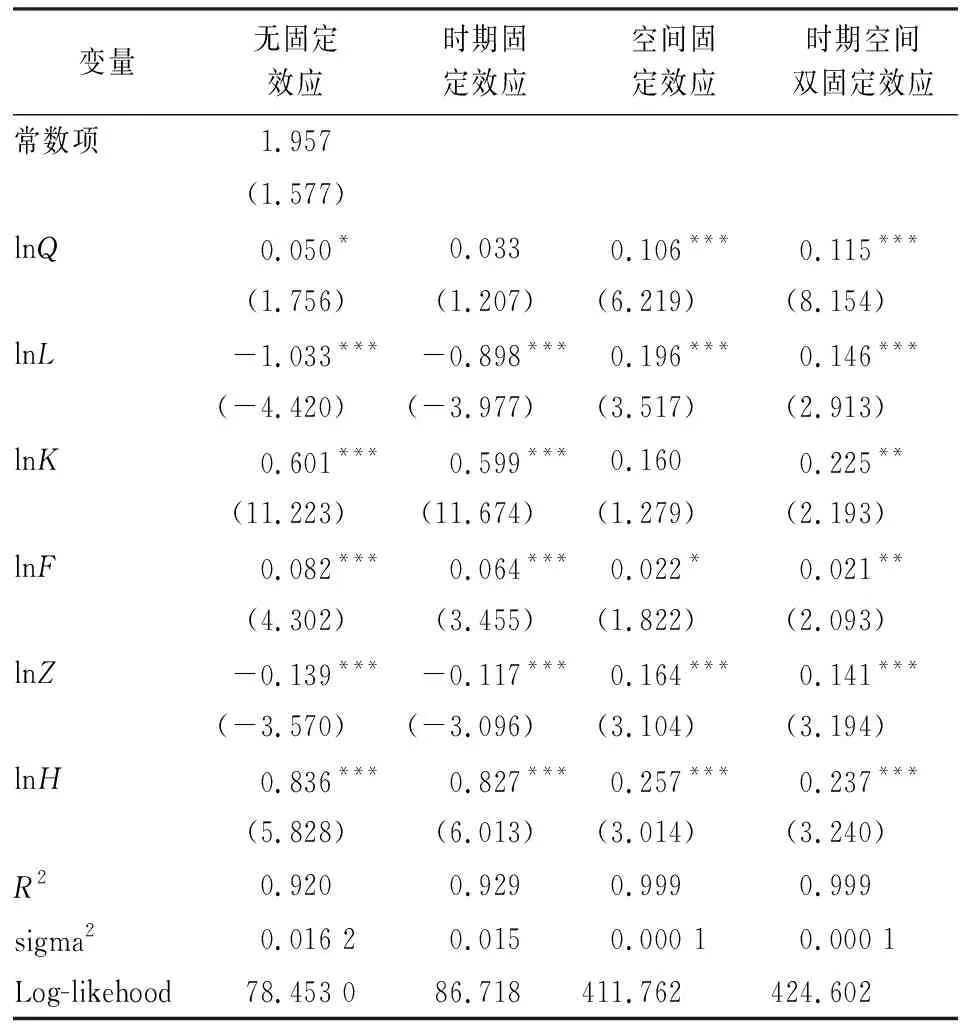
表5 不同交互效应下SDM模型的ML估计结果表

注：*、**、***分别代表0.1、0.05、0.01的显著性水平；括号里数字为相应变量系数的Asymptot t-stat值。

空间计量模型下，Log-likehood值的大小表明了拟合数据效果的优良。由表5可知，时期空间双固定效应下的SDM模型的Log-likehood值最高，且其拟合优度R2与离散度sigma2结果相对较好，再次证实了本研究中双固定SDM模型的优越性。另外，由表3和表5对比可以看出，与普通面板模型OLS估计结果相比，双固定效应下SDM模型的ML估计值显著性有了明显提高，这表明纳入空间效应后，普通面板模型的估计系数偏差得到了有效矫正。综上所述，选择更为一般的时期空间双固定SDM模型(13)研究制造业集聚对区域经济增长的影响机制最佳。

(三)双固定SDM模型空间效应分解分析

LeSage等人提出利用SDM模型设定的点估计方法来验证是否存在空间溢出效应或许会存在一定偏误，即自变量的系数估计值并不代表真实的偏回归系数[15]。因此，将时期空间双固定效应下的SDM模型(13)通过偏微分方式对空间效应进行分解(见表6)，其中直接效应代表本省域各解释变量对本地区经济增长的影响，间接效应表示本省域各解释变量对邻近地区经济增长的影响，而总效应则为直接与间接效应之和，即为各解释变量对经济增长的整体影响。

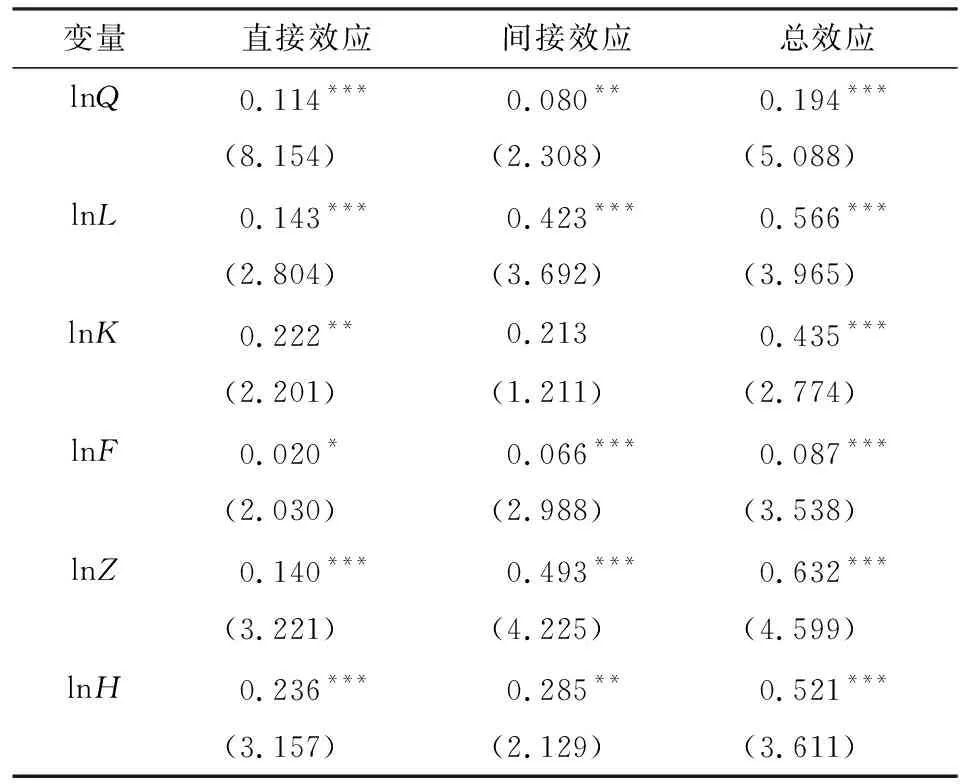
表6 时期空间双固定效应下SDM模型空间效应分解表

注：*、**、***分别代表0.1、0.05、0.01的显著性水平；括号里数字为相应变量系数的t值。

由表6各解释变量对区域经济增长的分解效应结果可知：

一是制造业集聚对区域经济增长的直接效应为0.114，且通过了1%的显著性检验，即当制造业的区位熵增加1%，在其他条件保持不变的情况下该省的实际人均GDP 将提高0.114%，这表明制造业集聚对本省域经济增长具有重要推动作用；其间接效应显著为正，说明制造业集聚水平的提高不仅能够拉动本省域的经济增长，且有利于邻近省域经济发展水平的提升，制造业集聚存在明显的空间溢出效应；制造业集聚与区域经济增长是相伴而生、休戚与共的统一体，制造业集聚实质是在市场开放的条件下各种资本要素合理流动且不断汇聚不断累积的动态过程，集聚所实现的共享劳动力市场、节约运输成本、技术外溢等外部规模效应都可以促进企业生产率的提高，进而促进区域经济增长；制造业集聚所产生的空间溢出效应又会带动周边地区的发展，产生由“极化效应”向“涓滴效应”的过渡，形成新的增长极，缩小区域发展差距。

二是人力资本投入对区域经济增长的直接效应与间接效应均显著为正，说明人力资本投入对促进区域经济增长水平具有明显的积极影响。内生增长理论模型认为，经济能够快速、持续、健康增长的主要动力已不再是物质资源而是知识、技术等人力资源。由总效应估计系数可以看出，人力资本投入的增加对区域经济增长的推动作用明显高于固定资产投资增加产生的促进作用，这也与潘文卿的研究结论相似[6]。

三是固定资产投资对区域经济增长的直接效应为0.222，且通过了5%的显著性检验，表明固定资产投资能够有效带动区域经济发展；投资与总产出之间存在着乘数效应，扩大固定资产的投入将会对经济增长产生成倍的拉动作用；固定资产投资的间接效应为0.213但并不显著，说明固定资产投资对邻近省域经济增长的作用程度较为有限。

四是技术创新的直接效应与间接效应的估计系数显著为正，但系数较小，均不足0.1，这表明R&D人员全时当量的增加对区域经济增长的作用微乎其微，通过提高R&D人员全时当量来促进区域经济增长还有很大的空间。

五是基础设施对区域经济增长的直接效应和间接效应均显著为正，基础设施是区域发展的硬环境。一方面，基础设施建设的完备能够为区域产业的高效发展提供安全有序、充满活力的硬件平台，为产业规模的扩大和地区产业向高附加值转化创造条件，促进区域经济增长；另一方面，基础设施将各个省域连成一个整体，能够促进各种经济要素的流动，降低企业交易成本，通过区域间经济活动的扩散对邻省域经济增长产生重要作用。

六是城市化对区域经济增长的直接效应为0.236，且通过了1%的显著性检验，而间接效应为0.285，通过了5%的显著性检验。Krugman认为在不完全竞争市场条件下，人口和经济集中有利于经济活动间的技术和金钱外部性，从而促进经济增长[16]111-117。因此，城市化不仅能够促进本省经济发展，同时对相邻省域的经济发展具有重要影响。

五、结论与建议

本文利用区位熵测算了2012—2015年中国31个省份制造业集聚状况，利用探索性空间数据分析方法验证了中国区域经济发展存在空间相关性，并据此构建空间计量模型，考察了制造业集聚对中国区域经济增长影响的空间溢出效应，其主要结论为：

第一，中国制造业集聚具有鲜明的区域差异特征。根据中国31个省份制造业区位熵测算结果可知，山东、江苏、河南、江西、广东、安徽、天津、浙江、吉林制造业集聚程度较高，全国制造业集聚大致呈现从东部地区向中西部地区逐渐降低的趋势。

第二，中国区域经济发展存有显著的空间自相关特征。从中国经济增长LISA集聚图中可以看出，中国目前形成了以江苏、上海为核心的“高-高”集聚区，以新疆、西藏、云南、贵州、青海、四川为主的“低-低”集聚区以及以河北为核心的“低-高”集聚区，其集聚模式呈梯度发展，东部地区经济增长水平较高，西部地区经济增长水平较低。

第三，中国制造业集聚能够有效促进区域经济增长。制造业集聚对区域经济增长的直接效应为0.114，间接效应为0.080，且均通过了5%的显著性检验，这表明在考虑了空间相关性和控制了人力资本投入、固定资产投资、技术创新、基础设施建设、城市化要素后，制造业集聚不仅会对本省域的经济增长起到促进作用，同时会对相邻省域经济增长产生一定的正向溢出效应。另外，由空间双固定效应下的SDM模型分析结果可知，各控制变量对区域经济增长具有明显的正向直接影响，除固定资产投资外也存在显著的正向溢出作用。

以上实证结果和研究结论表明，目前制造业集聚和经济发展水平并不平衡，制造业集聚对区域经济发展的空间溢出效应也呈现出显著的区域差异性特征。同时，制造业集聚与各生产要素都对区域经济增长产生了相应的直接作用与间接影响。因此，进一步优化中国制造业集聚的空间布局、促进要素之间的合理流动、推动中国区域经济的协调发展，显得尤为重要。据此，本文提出以下政策建议：

第一，引导产业合理布局，深化“示范效应”。中国制造业集聚存在着较为明显的区域差异特征，因此各地区政府应加快建设制造强国，实施制造强基工程，发挥政府的引导作用，形成合理的制造业布局，着力推动传统制造业向中高端迈进；各地区可以结合自身优势条件，重点培育适应市场需要、机制灵活、带动面广的特色制造业，进一步打造像舟山船舶产业集聚区、龙口有色金属加工业、上海民用航天基地等新型工业化优势产业示范基地以及独具特色的制造业集聚区，以集聚区内龙头企业为引导，充分发挥示范带头作用，吸引更多优质企业落户，从而使制造业集聚程度进一步提高，有效促进制造业结构优化升级以及区域经济的协调发展。

第二，打破地区产业封锁，强化“扩散效应”。由制造业集聚对区域经济增长的分解效应可知，制造业集聚不仅对本省经济增长具有促进作用，同时能够推动相邻省域经济的发展。因此，各地区应依托区域经济发展政策的“四大板块”、“三大战略”，不断完善区域制造业发展政策，重视制造业集聚的空间溢出作用，从而打破地区间制造业封锁及利益藩篱，强化扩散效应，辐射带动周边区域的发展，缩小邻近省域间经济发展差距。东部地区应凭借自身良好的区位优势，不断加强制造业集聚区的发展；而中西部地区在发展本地区优势制造业的同时，可以进一步优化制造业发展的硬环境和软实力，积极拓展制造业发展新空间，以便承接来自东部邻近地区的制造业转移，实现邻近区域间的产业承接与融合。

第三，促进区域要素投入，优化“乘数效应”。由各生产要素分解效应的估计结果可知，科技创新、固定资产投资、城市化、人力资本投入以及基础设施建设对区域经济增长的总效应都为正且影响程度依次增强，这表明促进区域经济增长和提高省域经济综合实力离不开这些要素的提升。因此，各地区应加强各资本要素的投入，加快基础设施建设，促进区域间要素自由流动，全面提高资源配置效率，同时发挥区域要素的乘数效应[17]，培育区域经济新增长极，为省域经济可持续发展创造源动力。