波动率合格代理变量的必要条件及其非参数检验

施雅丰，应婷婷，史彦龙，范奎奎

(1.宁波工程学院 理学院，浙江 宁波 315211；2.宁波诺丁汉大学 商学院，浙江 宁波 315100； 3.浙江医药高等专科学校 基础学院，浙江 宁波 315100；4.首都经济贸易大学 统计学院，北京 100070)

一、引言

波动率研究一直是金融资产定价和金融风险管理领域的热点问题，特别在近些年来中国大力发展多层次资本市场、持续推进股指(个股)期权等金融产品创新的背景下，波动率研究的应用价值和现实意义得以进一步凸显。

金融资产的真实波动率具有不可观测性，在学术研究和金融实务中常使用其代理变量(Proxy)来近似刻画真实波动率水平并将其用于评判波动率模型拟合效果好坏和预测能力高低，因此波动率代理变量的失当选择和评价准则的不稳健均有可能导致错误的评估结论。如Andersen、Hansen等指出采用代理变量替代隐变量得到的模型预测能力评价结果可能有失公允[1-2]；为了得到更稳健和可靠的评估结果，最近Patton给出了一族比较和评价波动率模型的评价准则[3]。但这些评价准则的稳健性建立在代理变量为真实波动率的条件无偏估计基础上。实际上，现有被选为波动率代理变量的估计量只有在理想假设下才为真实波动率的条件无偏估计量。例如，“已实现波动率”由于其在金融资产价格服从平方可积半鞅过程的假设下满足上述条件(Hansen 和Lunde)，而常被用来作为波动率代理变量，魏宇、杨科及王天一等均使用“已实现波动率”作为波动率代理变量[5-8]。因此，实际数据是否支持“已实现波动率”为真实波动率的条件无偏估计量是其成为合格代理变量的关键。但利用观察到有限的数据资源验证代理变量是否为条件无偏估计量存在巨大挑战，至今未发现有公开的文献对此问题进行探讨。基于由易及难的思路，本文导出合格波动率代理变量一个必要条件，然后给出验证这一必要条件的非参数方法。此研究虽然不能全面判别代理变量的合法性，但可以排除部分不合格的代理变量。

以中外股指高频数据为样本，利用新提出的方法检验各种“已实现波动率”是否违背本文提出的必要条件。实证结果表明：对于东亚的数据，“已实现波动率”违背了作为波动率代理变量的必要条件，而欧美数据未检测到此问题。最后，根据实证结果对“已实现波动率”进行适当改造，使其成为能避免上述偏差的改进代理变量。

二、合格波动率代理变量的必要条件和验证方法

rt=σtZt

(1)

其中，收益率冲击(return shock)Zt～iid(0,1)，t=1,2,…,T。

(一)合格波动率代理变量的必要条件

(2)

其中，p，q为给定的整数，f(·)为给定的函数表达式。该假设实际上对代理变量在信息域的投影进行设定。显然，这是一个比较弱但合理的假设，因为滞后项能涵盖其持续性，收益率能够反映过去的大部分信息。f(·)的选取通常有成熟的预测模型可借鉴。

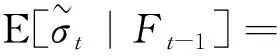
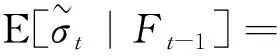
(3)

则称该代理变量为合格波动率代理变量。

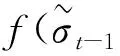
同理，从Rt～iid(0,1)可知子样本Rti～iid(0,1)，根据子样本方差的无偏性可知其期望为1；此外，相同样本量的样本方差的解释表达式相同，所以在样本独立同分布假设下具有相同的概率分布。从而得到推论1。

定理1给出了合格波动率代理变量的一个必要条件：若对应的波动率冲击被检测到存在某些子样本的分布不同，则可断定此代理变量不是合格的波动率代理变量。因此，定理1可用于排除部分不合适的波动率代理变量，从而可缩小寻找合格波动率的范围，进而可降低使用不恰当波动率代理变量进行相关研究的风险。由于检验两个数据集是否服从同一分布已经有许多成熟检验方法，例如KS检验等，所以定理1具有容易使用的优点。

依据推论1，若收益率冲击的某个子样本的样本方差显著大于1，则说明对应波动率代理变量低估了真实波动率，若显著小于1，则反之。所以，推论1除了具有利用子样本方差排除不合格波动率代理变量的作用外，还具有考查代理变量能否有效消除收益率异方差的作用。

(二)合格波动率代理变量必要条件的非参数检验

为了让推论1可用于排除不合格波动率代理变量，此部分将集中讨论关于子样本方差同分布的检验方法。考虑如下原假设，

H0：Rt中任意两个同样本量子样本的样本方差同分布。

由于Rt的分布未知，在原假设下导出其子样本方差的分布变得十分困难。若对Rt的分布进行设定，有设定误差风险。为了得到更稳健的结果，本文不设定Rt的分布，而利用原假设采用重抽样方法(bootstrap)构造子样本方差的置信区间，具体步骤如下：

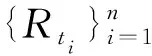
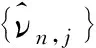
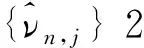
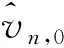
很显然，该检验方法避免了常用的方差检验所需要的正态分布假设，所以更具稳健性。这与推论1一起提供了一种通过某些目标子样本排除不合格波动率代理的非参数方法，其顺利实施的关键是找到合适的目标子样本。

三、基于中外股指高频数据的实证研究

使用上述方法分析基于高频数据的“已实现波动率”作为波动率代理变量的情况。

(一)“已实现波动率”与对应的收益率冲击

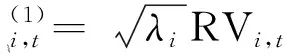
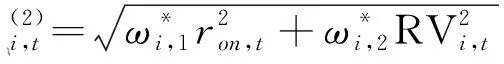
(4)

实证分析中本文采用Corsi 和Reno提出的 LHAR模型(式5)具体化假设1；然后，利用式(5)预测值计算收益率冲击Rt[14]。LHAR既能拟合已实现波动率的持续性又能刻画其杠杆效应，其对预测效应也得到学界一致认可。故选择它构造波动率代理变量在信息域(Ft-1)的条件均值有理论和实证保证。

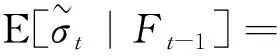
(5)

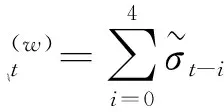
(二)样本数据和目标子样本选取

实证样本选用上证综指2001年2月28日至2013年3月28日的1分钟高频数据，数据来源为天相数据库。经整理，样本期内共有2 926个交易日，每个交易日有241样本数据(含当天开盘价)。

使用rcc,t、ron,t、roc,t分别表示隔日收益率(相邻两个交易日收盘价的对数差分)、隔夜收益率(前一交易日收盘价与当日开盘价的对数差分)和当日收益率(当日开盘价与收盘价的对数差分)滤掉趋势效应和周末效应的调整后收益率序列(收益率与常数、日期哑变量的线性回归模型的残差)。各调整后的收益率序列均值均为0，满足第二部分介绍的检验方法关于收益率条件期望为0的假设。使用样本数据分别计算6种“已实现波动率”，其基本描述统计量见表1。

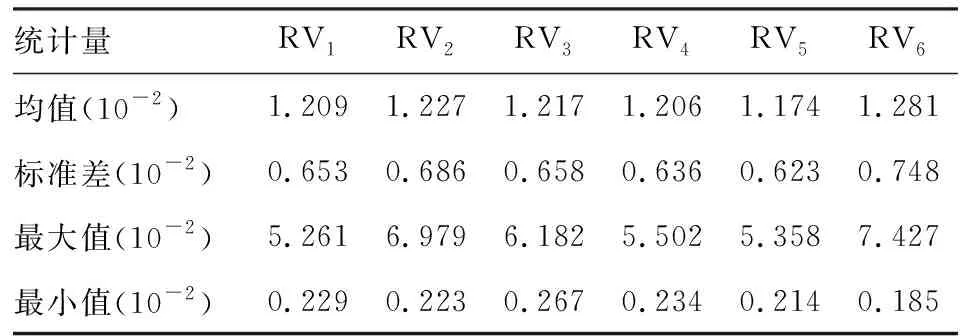
表1 “已实现波动率”估计的基本描述统计量

为考察市场结构性变化对检验结果的影响，根据上证综指5分钟收益率数据的偏自相关系数变动特征(见图1)，将全样本进一步分割为两个时间段，分别是2001年02月28至2007年05年31日(记为S1)和2007年06月01至2013年03月28日(记为S2)，并分别在S1和S2时段内检验“已实现波动率”是否为合格波动率代理变量，然后比较其检验结果。

(自上而下分别是1阶、2阶和3阶滞后)

基于波动率周内效应特征[15-16]，按周历日将样本分为5个子样本集作为检验的目标子样本。5个子样本分别记为：周1、周2、周3、周4和周5子样本。

(三)实证结果与中外比较分析

为了检验这些代理变量是否满足定理1，使用K-S双样本检验周1～5子样本两两之间收益率冲击的分布是否同分布，检验结果如表2所示。只有子样本周2和周3可以认为具有同分布，其它基本上拒绝同分布假设，而且大部分检验的P值特别小。这说明这些代理变量违背作为合格代理变量的必要条件，即定理1。为了观察国外的数据是否存在这样的问题，将其与标普500指数等股指数据进行比较，其结果如表3所示。对于欧美的股指基本上不存在上述问题，而东亚的股指数据存在类似的现象。这是一个有趣的新发现，其原因有待深入研究。

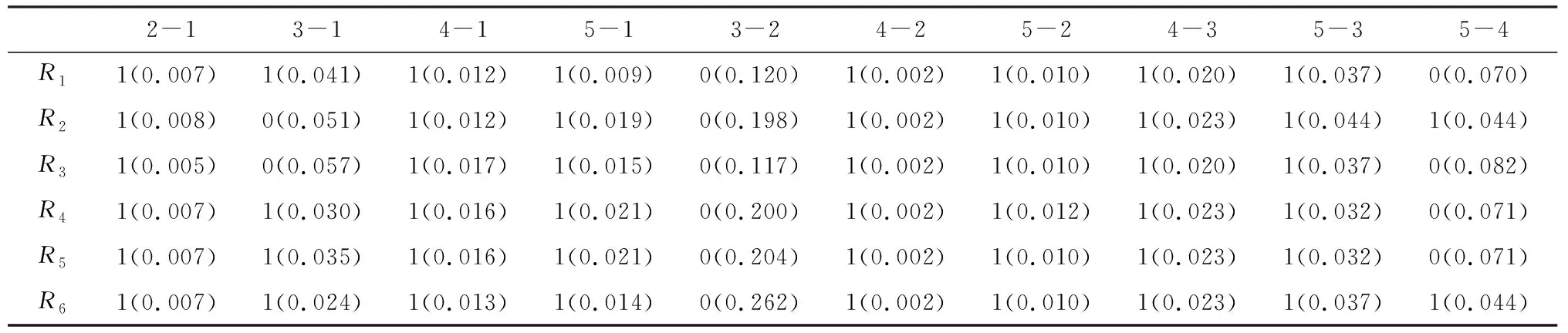
表2 上证综指的K-S检验结果

注：i-j表示子样本周i与周j的K-S检验；1，0分别表示在5%的显著水平下拒绝和不拒绝原假设(两个样本同分布)，()的数值为检验P值。

表3 中外股指的K-S检验结果

注：表中的数据表示6种代理变量对应的收益率冲击中拒绝原假设的数量。

为了进一步探究代理变量在每个子样本中是否高估或低估了真实波动率，采用本文提出的非参数检验方法对上证综指当日“已实现波动率”和全日“已实现波动率”[注]当日“已实现波动率”是指只使用交易时间高频数据计算得到的已实现波动率，其理论上是{roc,t}的波动率代理变量；它经比例因子或式(4)调整后记为全日“已实现波动率”，其理论上是{roc,t}的波动率代理变量。分别作为相应收益率波动率代理变量的合格性进行检验。

表4报告了全样本时段内的当日“已实现波动率”的检验结果：在周一和周二子样本的方差估计均未落入相应的置信区间。由此可断定，各波动率代理变量均在周一显著低估了上证综指的波动率水平，而在周二又都显著高估了上证综指的波动率水平。将样本分为S1样本时段和S2样本时段的进行相同的检验，得到了类似的结论，由此可见，市场结构性变化并未影响检验结论。

由此可见，对于中国股指的数据，采用“已实现波动率”作为代理变量在周一倾向于低估真实波动率水平，在周二易于高估真实波动率水平，故其不适合作为代理变量。而欧美股市的数据却未检测出上述问题。

(四)一种改进的波动率代理变量

一个自然的想法是通过适当的方式将其有偏的子样本方差调整为无偏，从而调整后的“已实现波动率”作为波动率代理变量可以避免出现上述在某些子样本低估或高估的问题。因此，在每个子样本中采用类似式(5)的方式调整“已实现波动率”，调整表达式为：

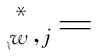
j=1,2,…,5

(6)

显然，由式(6)给出的新波动率代理变量既能充分利用高频信息和隔夜信息，又能避免上述实证中所出现的问题。

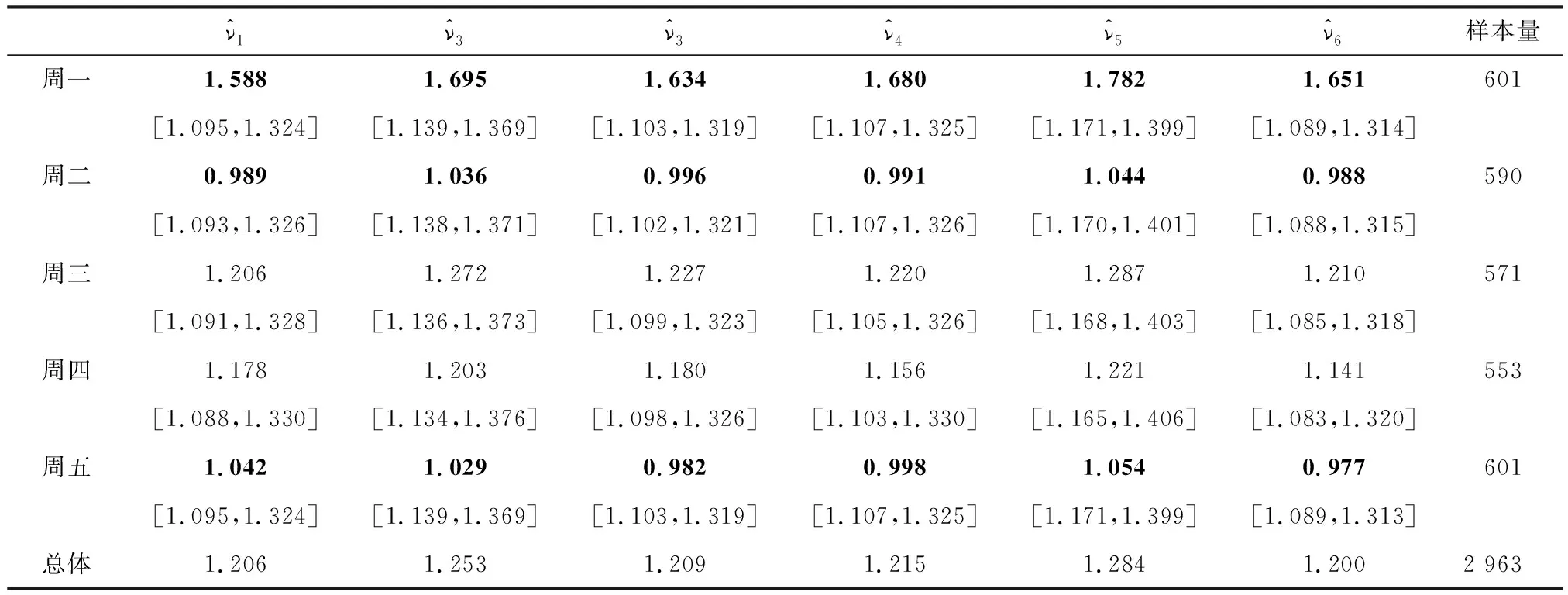
表4 上证综指的波动率代理变量适应性检验结果

注：[ ]为置信度为95%的区间估计量，表中粗体表示统计量与置信区间不一致；重抽样次数为10万次。

四、结束语

波动率代理变量的选择恰当与否直接影响波动率模型比较的结果和波动率预测精度的评价，若能给出检验一个波动率代理变量是否合格的方法对波动率研究具有重要意义。本文虽然没能给出一个检验波动率代理变量是否合格的方法，但提出了通过合格波动率的必要条件，并用其排除部分不合格波动率代理变量的研究途径。因此，本研究的一个重要意义在于给出了一个检验潜在合格代理变量新的技术路线。此外，本文给出的非参数检验方法，采用重抽样的方法构造置信区间，此方法与参数方法比较具有：(1)不需要对收益率分布进行参数假设，可以避免设定误差的优势，从而具有较强的稳健性；(2)可避免繁杂的统计量分布推断过程，其局限性在于重抽样需要较大样本量和计算量及要求使用者有一定编程能力。

基于中外股指高频数据的实证研究表明：对于中国股指的数据，采用“已实现波动率”作为代理变量有在周一(周二)低估(高估)真实波动率水平的问题，违背了合格波动率代理变量的必要条件，因此将其作为波动率代理变量的适合性欠佳。如果这些波动率代理变量被用于中国股票市场波动率预测模型比较，易造成与实际情况不相符的结论。欧美股市的数据未检测出违背必要条件的问题，这是一个值得深入探究原因的现象。

最后，根据实证结果，对文中讨论的“已实现波动率”进行适当的改造以提高其适用性，使其成为能避免实证中所出现的系统偏差的新代理变量。希望此研究能起到抛砖引玉的作用。