引入外部冲击的中国铜期货市场高频波动率建模与预测

朱学红，邹佳纹，韩飞燕，谌金宇

(1.中南大学商学院，湖南 长沙 410083；2．中南大学金属资源战略研究院，湖南 长沙 410083)

1 引言

随着人们对金融资产的分配及风险管理的日益关注，金融市场波动率建模和预测成为人们关注的焦点，它在资产配置、金融风险管理、金融衍生品的定价以及投资组合策略的选择等方面都有着非常广泛的应用。由于有色金属期货市场是资本市场的重要组成部分，且有色金属期货市场是反映国民经济运行状况的窗口之一，同时在全球经济格局发生转变的背景下，不时出现的国际流动性过剩、能源商品价格上涨以及大宗商品期货指数化投资等外部因素的变化深刻影响着有色金属期货市场。为此，本文尝试将影响我国有色金属期货市场波动率的外部冲击因素引入波动率模型中，以期提高有色金属期货波动率模型的拟合效果及预测能力，为期货市场投资者提供风险管理的有力工具。

早期对金融波动率预测模型的研究使用日数据或更低频数据，把波动率视作不可观测的隐变量，通过对收益条件方差建模间接刻画。20世纪80年代Engle[1]提出的自回归条件异方差(Autoregressive Conditional HeteroskedAsticity，ARCH)模型，以及Bollerslev[2]在此基础上提出的GARCH模型，较好地刻画了金融波动率的长记忆性，因此得到了学者们的广泛关注，并拓展出EGARCH模型[3]、FIGARCH模型[4]等各种形式；然而，随着计算机技术的迅速发展，日内高频交易数据成为研究金融波动率的重要数据时[5-6]，Hansen和Lunde[7]研究指出，复杂GARCH族模型的样本外预测能力并不优于最初的GARCH(1，1)模型。诸多研究者试图构造合适的模型以期利用高频数据来提升模型的精确度。其中，Andersen和Bollerslev[8]，Andersen等[9]，以及Barndorff和Shephard[10]等提出以日内高频收益平方和计算的“已实现波动”(Realized Volatility，RV)作为真实波动率的估计量，从而使金融波动率由隐变量转变为可以直接建模刻画的显变量。在已实现波动的建模方面，Corsi[11]的HAR-RV(Heterogeneous Autoregressive model of the Realized Volatility)模型将市场波动视作高频、中频、低频交易者共同作用的结果，通过对一日、一周、一月三种不同时间尺度已实现波动自回归过程的叠加较好刻画了波动持续性，而且可以用OLS进行估计，因此逐渐代替了缺乏明确经济诠释的分整模型(Fractionally Integrated Model)从而得到了广泛应用。Andersen等[12]在此基础上提出区分跳跃波动与连续波动的HAR-RV-J与HAR-RV-CJ模型，并实证指出引入平方根与对数变换可以提高模型的拟合能力。张小勇和任德平[13]在HAR-RV-CJ模型的基础上考虑隔夜信息的影响，对模型进行扩展最终形成了HAR-RV-CJN。瞿慧等[14]指出HAR族模型相比以往基于低频数据的模型有着更好的预测精度。由于模型优良的预测性能，近年来不少研究者都采用了HAR族模型对金融市场的波动率进行研究[15-19]，至此HAR族模型得到了广泛的应用。

另一方面，随着经济全球化的深入发展，中外市场的联动性越来越强，中国有色金属期货市场越来越容易受到外部冲击。在此背景下，许多学者日益关注外部冲击对我国有色金属期货市场的影响。纪敏[20]、尹力博和韩立岩[21]构建了外部冲击影响有色金属等大宗商品价格的分析框架，将外部冲击划分为需求拉动冲击、成本推动冲击和货币冲击三类。对于需求拉动冲击的影响，在开放型经济条件下，随着我国对国际有色金属市场依赖程度的加深，我国有色金属价格必然会受到国际需求的影响[22-23]。对于成本推动冲击的影响，石油价格是有色金属生产成本的主要组成部分，会直接造成有色金属价格相应变化，因此许多学者探讨石油价格的成本推动作用[24-26]；对于货币冲击的影响，学者们重点关注利率、美元汇率及股票价格的影响，由于美元是铜等有色金属的结算货币，在其他条件不变时，美元币值变动会影响有色金属价格变动，黄健柏等[27]、Zhu Xuehong等[28]探究了美元汇率对中国金属价格的影响。而当利率变动时，融资成本的变动也会引起价格变动，同时，一般利率特别是联邦基金利率会与美元汇率发生同向变动，从而间接通过美元汇率影响有色金属价格，至于股票价格在某种程度上代表货币金融因素，其对金属等大宗商品价格也具有重要影响[29-30]。

然而到目前为止，尚未有学者研究过引入外部冲击指标对铜等有色金属期货波动率模型预测性能的改进，鉴于此，本文使用中国有色金属期货市场中铜价格的高频波动率数据作为样本，建立HAR-RV-CJN模型，并在此基础上以加性形式引入外部冲击变量改进提出HAR-RV-CJN-ES模型。最后，文章还实证检验了引入外部冲击变量是否改进已实现波动模型的拟合效果和预测能力，并将HAR-RV-CJN-ES模型与HAR-RV-CJ、HAR-RV-CJN模型在拟合度与预测能力上进行对比。在具体分析中，由于铜是具有代表性的金属，上市交易早、发育成熟、成交量大、流动性较好，数据的可得性和时间序列能很好满足实证需要。所以，本文以铜为例展开分析。

2 理论基础

2.1 HAR-RV模型

已实现波动率(RV)是基于日内高频数据的波动度量，Andersen和Bollerslev[8]将已实现波动率定义为日内高频收益率的平方和。将每个交易日分为M个时间段，第t日第j个区间的最后一个交易价格称为pt,j,第t日的开盘价为pt,o，收盘价为pt,c，第t个交易日第j个时间段的收益率记为：

rt,j=lnpt，j-lnpt，j-1(j=1,2,3,…,M)

(1)

则第t个交易日的已实现波动率可以表示为：

(2)

现实的金融市场往往存在各种风险，风险套利广泛充斥在市场的各个角落，因此，金融资产的价格不再是连续的，而是存在各种跳跃性波动，金融资产的对数价格在整个交易期间服从一个标准的连续跳跃离散过程[31]，该过程以随机差分形式表示如下：

dp(t)=μ(t)dt+σ(t)dW(t)+k(t)dq(t)

(3)

其中μ(t)是连续且局部有限变动的漂移系数，σ(t)>0表示随机波动过程，W(t)是标准布朗运动，q(t)是一个强度(单位时间内发生跳跃的次数)为λ(t)的计数过程，k(t)dq(t)表示纯跳跃部分。如果资产价格在t时刻有跳跃，那么dp(t)=1，否则，dp(t)=0；k(t)表示跳跃的幅度。跳跃的幅度k(t)和频率λ(t)均为时变变量。

基于以上假设，二次变差可以分解为随机波动所组成的连续变差Ct以及跳跃所带来的非连续变差Jt两部分，可以表示为：

(4)

其中右边第一项称为积分方差(Integrated variance，IV)，也叫连续变差部分(Ct)；右边第二项是由价格过程的跳跃部分所形成的二次变差，也叫跳变差部分(Jt)，其中Nt表示在第t日跳跃发生的次数，kt,j表示第t日第j个跳跃的幅度。

根据Barndorff和Shephard[32]的研究，若资产价格过程不存在跳跃，当取样频率趋于无穷大时，已实现波动率是积分方差的一致估计；若资产价格过程存在跳跃时，已实现波动率依概率收敛于二次变差过程，即

(5)

研究采用Barndorff Xin和Shephard[32]所提出的已实现双幂次变差(RealizedBipower Variation, RBV)以及相应的跳检验统计量(Zt)将已实现波动率中的连续部分和跳跃引起的非连续部分分离。

(6)

(7)

结合式子(3)和(7)可以得出，已实现波动率RVt(M)和已实现双幂次变差RBVt(M)之差依概率收敛于二次变差过程中由跳跃形成的部分。

(8)

即在考虑跳跃过程的基础上，已实现波动率的收敛结果除包含积分方差之外，还包含了跳跃对已实现波动率的影响。

研究采用Huang Xin和Tauchen[33]所提出的近似服从正态分布的跳检验统计量Zt检验跳跃的存在性：

(9)

其中RQVt是t日的四次方变差的估计量：

(10)

若资产价格过程不存在日内跳动，则Zt服从渐进标准正态分布，通过它可以检验已实现波动率是否存在跳跃。

基于跳检验统计量Zt，二次变差中的跳变差部分Jt可以用下式进行度量：

Jt=I(Zt>Φα)·(RVt-RBVt)

(11)

其中I为示性函数，Φα表示标准正态分布在显著性水平α下对应的临界值，本文选取α=0.99。相应的，二次变差中的连续部分的度量可以表示为：

Ct=I(Zt≤Φα)·RVt+I(Zt>Φα)·RBVt

(12)

在异质市场假说的基础上，Crosi[11]提出了HAR-RV模型，具体模型如下：

(13)

(14)

(15)

(16)

2.2 HAR-RV-CJ模型

在HAR-RV模型的基础上，Andersen等[12]首次考虑了跳跃方差对已实现波动率的影响，建立了HAR-RV-J模型，并进一步将已实现波动率分离成连续样本路径方差和跳跃方差，构建了HAR-RV-CJ模型，具体模型形式如下：

(17)

(18)

(19)

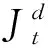
(20)

(21)

2.3 HAR-RV-CJN模型

Hansen和Lunde[34]将隔夜收益波动率纳入到已实现波动率预测的研究考虑范围之内，并给出了隔夜收益方差的建模估计方法，张小勇和任德平[13]将隔夜波动率、连续样本路径方差及离散跳跃方差纳入到已实现波动率的预测研究范畴，构建了HAR-RV-CJN模型。具体模型形式如下：

(22)

(23)

(24)

2.4 基于SPA检验的预测模型比较

本文综合参考魏宇和余怒涛[35]、王鹏和王建琼[36]、瞿慧和程思逸[18]的研究成果，采用如下四种常用损失函数作为样本外预测精度的衡量标准：

(25)

3 HAR-RV-CJN-ES模型

本文借鉴依据纪敏[20]、尹力博和韩立岩[21]的分析框架，从外需拉动冲击、成本推动冲击和货币冲击三个层面选取外部冲击变量。对于外部需求冲击，本文依据钟美瑞等[37]，选取伦敦金属交易所的期铜库存作为外部需求的代表，记为STOCK，铜库存增加，反映铜需求减小，铜库存减少，则反映铜需求增加；其次对于成本冲击，由于石油价格是铜生产成本的主要组成部分，会直接造成有色金属价格相应变化，因此本文依据Baffes[24]、Hammoudeh等[25]和Soytas等[26]，选取WTI原油价格作为成本冲击的替代变量，记为OIL；对于货币冲击，由于汇率的波动会直接造成我国铜进出口相对价格的变动，利率的高低能够反映市场参与者的资金成本，从而推动铜价格的波动，而随着国内外股票市场的联动性的增强，大量的机构投资者参与跨市交易，股票价格作为货币金融因素，对我国铜期货价格产生重要影响，因此本文分别依据Zhu Xuehong等[28]、钟美瑞等[38]、田利辉和谭德凯[29]的研究选取美元指数、联邦基金利率和标普500指数作为货币冲击的代表，分别记为INDEX、INTEREST、BIAOPU。

研究对外部冲击指标进行主成分分析后提取的具有代表性的成分F1，F2，作为外生变量引入HAR-RV-CJN模型中，建立HAR-RV-CJN-ES模型，具体形式如下：

(26)

其中，n为引入的主成分数，对系数βCD、βCW、βCM的估计表示不同周期的连续样本方差对已实现波动率的影响，βJD、βJW、βJM直接度量了不同周期跳跃方差对已实现波动率的影响，βND、βNW、βNM的估计值则衡量不同周期的隔夜波动率对已实现波动率的影响，同理，通过对θi系数的估计，能够知道每个主成分对已实现波动率的影响程度，即引入的外部冲击变量对已实现波动率的预测能力相对于HAR-RV-CJN模型是否有进一步改善。

4 实证检验

4.1 数据处理

类似于Xu Xiaoqing和Fung[38]、朱学红等[39]的铜期货数据选择方式，本文选取上海期货交易所3个月到期的铜期货的1 分钟收盘价高频数据为研究对象，样本区间为2010年7月1日至2015年6月30日，同时选取同期外部冲击指标数据，数据来源于Wind数据库。

标普500指数、美元指数、联邦基金利率、原油价格和国际库存这五个外部冲击指标之间部分存在较强的相关性，因此有必要进行主成分分析。主成分分析的分析结果如表1所示。存在2个特征值均大于1的主成分，其累计贡献率达到80%左右，因此通过对五个外部冲击指标的主成分分析，提取出主成分F1，F2。

主成分载荷如表2所示，标普500指数、国际库存在第一主成分上拥有较高的载荷，而美元指数、联邦基金利率和原油价格在第二成分上拥有较高载荷。为了挖掘各主成分的经济含义，本文依据韩立岩和尹力博[30]，将各主成分对信息集内的变量进行回归分析，并依据R2值最高的指标提取主成分信息。从回归结果看，F1主要反映国际库存信息，而F2则主要反映联邦基金利率信息。

表1 外部冲击指标主成分分析结果

表2 主成分载荷

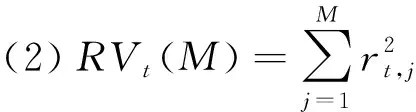
对已实现波动率、连续变差部分、跳跃变差部分、隔夜波动率及其对数形式的8个时间序列进行描述性统计，结果如表3所示。

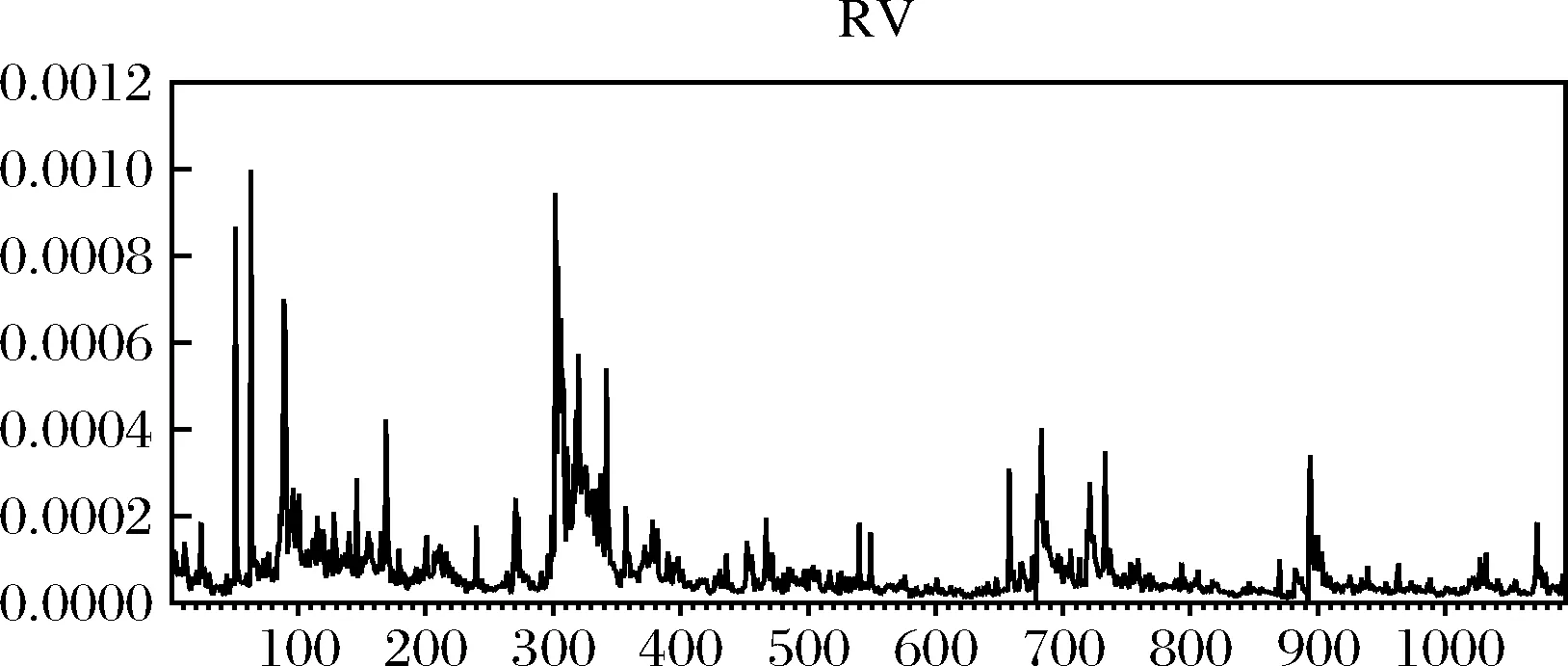
图1 期铜的已实现波动率趋势图

图2 期铜的连续变差部分趋势图

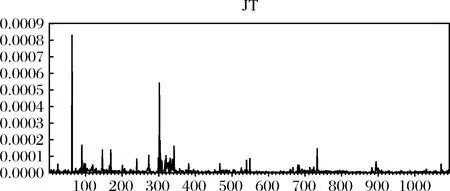
图3 期铜的跳跃变差部分趋势图

图4 期铜的隔夜波动率趋势图

从表3可知，从各变量的正态性来看，已实现波动率、连续变差部分、跳跃变差部分和隔夜波动率四个统计量的原序列的偏度和峰度都呈现出右偏和尖峰特征，而原序列的对数形式更接近于正态分布，因此，在后面的已实现波动率建模中，对各变量采取对数形式。

4.2 模型的估计与拟合结果分析

为了从不同的角度全面揭示我国期铜高频波动率的特征和规律，分别对HAR-RV-CJ模型、HAR-RV-CJN模型以及HAR-RV-CJN-ES新模型进行参数估计，结果如表4所示。

为了更全面的检验三种波动方差对期铜已实现波动预测的影响，选取H=1、5、22，即：RVt+1、RVt+5、RVt+22分别代表短期、中期和长期的已实现波动率，然后对HAR-RV-CJ、HAR-RV-CJN和新构建的HAR-RV-CJN-ES模型采用Newey-West法进行参数估计，三种模型的估计结果如表4所示：

表3 日波动率成分的描述性统计

注：***、**、*分别表示在1%、5%、10%的显著性水平下显著

表4 参数估计结果

注：方括号内为系数所对应的标准差，*、**、***分别表示10%、5%、1%的显著性水平下显著。其中M1=HAR-RV-CJ；M2=HAR-RV-CJN；M3=HAR-RV-CJN-ES。

在表4中，通过对HAR-RV-CJ模型各区间的估计系数进行细致分析，可以发现期铜短期(H=1)和中期(H=5)的已实现波动率的预测上，不同周期连续变差部分对其具有显著的影响，而不同周期的跳跃变差部分对已实现波动边际影响的各系数都不显著，则说明短中期内对于期铜已实现波动率的预测主要依赖于连续变差部分，对于跳跃变差部分的信息在铜期货市场还未得到及时反馈。对于长期(H=22)的已实现波动率的预测估计上，不同周期的连续变差部分和跳跃变差部分在一定的置信水平下都对其产生显著的影响，说明在长期上已实现波动率的预测依赖于连续和跳跃两个波动成分，这意味着过去的连续和跳跃波动对未来已实现波动率存在持续性的影响。跳跃波动对未来已实现波动率在长期造成显著影响的原因可能是由于以往导致跳跃波动的信息能够在经过较长时间的传递后被投资者所认知，进而影响到未来已实现波动率。

通过分析HAR-RV-CJN模型的参数估计结果可以发现，与HAR-RV-CJ模型的估计结果类似，HAR-RV-CJN模型在H=1和H=5的短中期内，大部分的跳跃波动部分和隔夜波动率的估计参数不显著，则表明在短中期内只有连续波动部分对期铜已实现波动率的预测发挥作用。在H=22的长期已实现波动率的预测中，大部分的跳跃波动部分以及全部的隔夜波动率都对其预测产生显著的影响，未来的已实现波动率会受到隔夜信息波动的持续性影响。而对于长期内连续变差部分和跳跃变差部分进行观察可知，月连续变差部分βCM和日跳跃变差部分βJD的参数估计与HAR-RV-CJ模型相比较已变为不显著，造成这种影响的原因可能是隔夜波动率的加入稀释了这两部分对已实现波动率的影响，也就是说隔夜波动率也是导致期铜价格波动的一个重要原因。

HAR-RV-CJN-ES模型的参数估计结果显示，在短中期内HAR-RV-CJN-ES模型的估计结果与HAR-RV-CJ模型和HAR-RV-CJN模型的结果类似，连续变差部分的参数估计显著，而跳跃变差部分、隔夜波动率和外部冲击变量对其不产生显著的影响，期铜的已实现波动率仍由连续变差部分决定。但在H=22的长期已实现波动率的预测上，引入的外部冲击变量的估计参数θ1、θ2变得显著，这说明外部冲击变量对长期内期铜已实现波动率的预测产生不可忽略的的影响，也表明外部冲击部分对已实现波动率的影响具有较强的滞后效应。

并且从参数正负情况来看，主要反映国际库存信息的主成分F1的参数θ1的方向为负，表明国际库存增加，期铜价格下降，符合理论预期；而主要反映联邦基金利率信息的参数θ2的方向为正，与预期相反，依据钟美瑞等[38]，这主要是由于目前美联储制定货币政策基本上遵循泰勒法则，也就是盯住目标的经济增长率和通货膨胀率。因此，美国联邦基金利率的提高与美国经济的成长是正向关系，从而构成了与铜价之间的正向关系。

将引入外部冲击变量后的HAR-RV-CJN-ES模型在短期(H=1)、中期(H=5)和长期(H=22)已实现波动率的拟合效果与HAR-RV-CJ模型和HAR-RV-CJN模型进行比较与分析，整理结果如表5所示，调整后的拟合值(R2)代表各模型对未来不同时期已实现波动率的拟合效果，R2越大则代表拟合效果越好。

通过对表5的结果分析可知，一方面HAR-RV-CJ模型、HAR-RV-CJN模型和HAR-RV-CJN-ES模型对于未来已实现波动率的拟合效果从短期到长期逐步提高，这与前面的各模型的参数估计结果一致。另一方面，对于引入外部冲击变量的HAR-RV-CJN-ES模型与其它模型相比较，无论是在短期、中期还是长期中，调整后的R2值都有所提高，表明新建的HAR-RV-CJN-ES模型提高了现有模型的拟合优度，外部冲击变量作为波动率的重要的外部影响因素，它的加入提高了模型的波动解释能力，其中对于提高幅度长期最为显著，中期次之，短期最小，分别为4.37%、0.81%和0.28%。

表5 模型的拟合结果

4.3 高频波动率模型的预测能力分析

利用引入外部冲击的HAR-RV-CJN-ES模型对期铜的波动率进行预测，与HAR-RV-CJ模型和HAR-RV-CJN模型的预测结果进行比较，并对各模型的预测能力进行分析。

本文将实证的数据区间按照4：1 的比例进行样本外预测，其中2010年7月1日至2014年6月30日为估计区间，2014年7月1日至2015年6月30日为预测区间。表6是经过1000次bootstrap模拟过程后的SPA检验结果。

由表6可以看出，短中期内，隔夜信息的加入使得HAR-RV-CJN模型的预测精度较HAR-RV-CJ模型有了小幅提升，而长期这种提升比较显著。外部冲击信息的加入使得HAR-RV-CJN-ES模型的精度在短中期相对于HAR-RV-CJN和HAR-RV-CJ并没有显著提升。然而在长期，引入外部冲击后的HAR-RV-CJN-ES模型在四种损失函数标准下其P值均接近1，这说明在长期内已实现波动率的预测HAR-RV-CJN-ES模型的预测精度要远好于HAR-RV-CJN和HAR-RV-CJ模型。

表6 模型的预测能力的SPA检验

注：括号内依次为MSE，MAE，HMSE，HMAE损失函数标准下所对应的P值

5 结语

本文在总结高频波动率研究理论和模型的基础上，采用上海期货交易所的高频交易数据对我国期铜波动率的度量和预测展开深入的研究，对一系列的外部冲击变量进行相关系数分析与主成分分析，降低外部冲击变量的维度，提取相应的主成分，进而将主成分引入现有的高频波动率模型，建立HAR-RV-CJN-ES模型，并对模型的拟合效果与预测精度进行了分析。本文的主要结论如下：

(1)在短中期内，HAR-RV-CJN-ES模型连续变差部分的参数估计显著，而跳跃变差部分、隔夜波动率和外部冲击变量对其不产生显著的影响，期铜的已实现波动率仍由跳跃变差部分决定。但在长期已实现波动率的预测上，外部冲击变量对期铜已实现波动率的预测产生不可忽略的影响。

(2)对引入外部冲击变量后的HAR-RV-CJN-ES模型的拟合效果从短期到长期逐步提高。无论是在短期、中期还是长期中，调整后的R2值都有所提高，HAR-RV-CJN-ES模型提高了现有模型的拟合优度，外部冲击变量作为波动率的重要影响因素，它的加入提高了模型的解释能力，其中提升幅度在长期最为显著，中期次之，短期最小。

HAR-RV-CJN-ES模型对有色金属期货波动率预测效果的提高，可以为有色金属期货市场风险管理提供可靠的依据，同时也为期货投资者提供了良好的借鉴意义，以使其更好地进行期货市场波动率的建模预测。下一步可根据该思路选择影响不同期货品种的相应宏观经济指标，将模型应用于其他商品期货以及指数期货的波动率建模中，同时可进一步分析研究期货市场波动率的独特性，基于已有波动率模型从不同角度进行模型的优化改进，以提髙期货市场波动率的预测能力。