目标导向层次分析方法

李春好，李 巍，何 娟，李孟姣，马慧欣

(吉林大学管理学院，吉林 长春 130022)

1 引言

Saaty为解决具有层次结构的复杂评价与决策问题所提出的层次分析法(AHP—Analytic Hierarchy Process)[1-2]，尽管迄今已在许多领域获得了非常广泛应用[3]，但由于在决策方案评价时会出现逆序(即在备选方案集中增加或减少一个方案后AHP会对其它方案给出不同的优劣排序结果)等问题，也持续不断地受到了许多学者针对其正确性的学术质疑[4-16]，著名管理学家Smith和von Winterfeldt[4]甚至认为AHP存在着根本性错误。尽管如此，Saaty虽在AHP原有分布式分析模式(Distributive Mode)的基础上又提出了绝对分析模式(Absolute Mode)、理想分析模式(Ideal Mode)和超矩阵分析模式(Supermatrix Mode)[17],但并没有从方法核心上直面学术界的质疑，即使在近来发表于著名学术期刊Operations Research的总结性撰文中仍然坚持维护AHP的正确性[3]。下文为叙述方便，分别将对应上述四种分析模式的AHP称为DIS-AHP、ABS-AHP、IDE-AHP和SUP-AHP方法。

在保证属性结构(即不含方案层的层次结构)不变的条件下，ABS-AHP、IDE-AHP和SUP-AHP与DIS-AHP不同，能够克服方案评价逆序问题[3,17]。

但从方法程序上讲，ABS-AHP、IDE-AHP和SUP- AHP与DIS-AHP的不同之处仅在于针对层次结构最底层单层排序权重(即备选方案相对于其上一层次某个属性的排序权重)的判断模式存在差异，而在其它层次上关于单层排序权重的判断模式是完全相同的，即均与DIS-AHP针对单层排序权重(包括层次结构最底层的单层排序权重)的判断模式完全相同[17]。由此需要强调指出，尽管ABS-AHP、IDE- AHP和SUP-AHP能在形式上克服方案评价逆序问题，但若DIS-AHP在单层排序权重上的判断模式存在问题甚至是错误，那么也不能因ABS- AHP、IDE-AHP和SUP-AHP不出现逆序问题而断言它们就是科学合理的评价与决策方法。

关于DIS-AHP在单层排序权重(包含最底层单层排序权重)上的判断模式，迄今已有许多学者予以了质疑与批评[4-9,14-16,18]。例如，针对其采用的相对上层一个系统元素(属性)来以比率(先以语言描述后对语言描述进行比率赋值)比较下层元素(属性或方案)之间相对重要性(相对偏好)的判断模式，Belton和Gear[5-6]、Dyer[7-8]、Smith和von Winterfeldt[4]等许多学者认为其中缺少比率比较的基准“0”点。由此，他们认为这种比率判断即使对于一个富有经验的决策者而言也是难以实现的；即使决策者给出了相关判断，那么由此得出的单层排序权重在内涵上也是模糊不清的。尽管Saaty[2]关于相对偏好的比率比较给出了相关原理，但Dyer[7]认为这些原理仅是原生性(Primitive)看法并由此建议采用具有可靠理论基础的多属性价值理论去取代关于相对偏好比率比较的原生性原理。Smith和von Winterfeldt[4]也类似地批评指出，Saaty给出的原生性原理与多属性效用理论和多属性价值理论不同，并不能通过决策者的选择行为对DIS- AHP所采用的偏好独立假设予以适用性检验。

为克服比率比较基准的缺失问题以发展DIS- AHP，Belton和Gear[5]提出应将最理想虚假方案(其在最底层属性上的属性值为备选方案在对应最底层属性上的最优值)作为比率比较的基准“0”点，并由此提出了对DIS-AHP的改进方法(学术界将之称为B-G-AHP方法)；Schoner和Wedley[14]提出应将平均虚假方案(其在最底层属性上的属性值为所有备选方案在对应最底层属性上属性值的平均值)作为比率比较的基准“0”点，并由此提出了改进DIS-AHP的Reference-AHP方法。基于类似思想，Schoner等[15]为发展DIS-AHP还提出了能够比B-G-AHP方法和Reference-AHP方法更具有一般性的LP(Linking pins)-AHP方法。需要指出，由于对应评价与决策问题的层次结构中只有最底层属性是具体属性，能够由此给出虚假方案在这些属性上的属性值，而其它属性则为抽象属性、难以给出虚假方案在这些属性上的属性值，因此无论是Dyer[7]所提出的采用多属性价值理论去取代DIS-AHP原生性原理的方法改进建议，还是上述针对DIS-AHP的各种改进方法，对于含有抽象属性的层次结构而言并没有从根本上克服比率比较基准“0”点缺失问题以及与此相关的单层排序权重内涵模糊不清问题。

为克服DIS-AHP的方案评价逆序问题，学术界还在权重(包含单层排序权重和关于方案优劣排序的复合权重)处理方法上进行了多方面研究探索。 Ramanathan[13]通过把数据包络分析技术(Data Envelopment Analysis-DEA)[19]引入到DIS-AHP，提出了旨在方案评价保序的DEAHP方法，但Wang和Elhag[20]通过反例证明DEAHP方法也会出现逆序问题，并基于元素(方案或属性)增减后单层排序权重应保持不变视角提出了旨在方案评价保序的DIS-AHP改进方法(下文称为W/E-AHP方法)，其后Maleki和Zadeh[21]又通过反例证明W/E-AHP方法也会出现逆序问题。Barzilai与Lootsma[10]和Lootsma[11]认为，在计算方案复合权重时若采用乘法算子取代DIS-AHP的加法算子，则能够实现方案评价保序，但Vargas[22]通过反例证明采用乘法算子计算方案复合权重是无效的。上述研究状况表明：在权重处理上学术界迄今也没有给出克服DIS- AHP方案评价逆序问题的有效方法。

综上所述，对于层次系统结构中含有抽象属性的决策问题而言，无论是DIS-AHP还是ABS-AHP、IDE-AHP和SUP-AHP都会因其中存在的比率比较基准缺失问题、权重内涵模糊不清问题或权重处理对于方案评价不能保序问题而较为缺乏科学理性。

为解决上述问题并着眼于现实层次性评价与决策问题通常含有抽象属性的决策需求，下文沿循Dyer[7]发展AHP的学术思想，基于拥有健壮多属性价值理论基础的摆幅置权(Swing Weighting—SW[23])判断模式和李春好等[24]给出的多属性决策属性价值公度方法，首先给出能够为层次结构抽象属性上的SW判断提供支持的规约性(Prescriptive)多属性决策属性价值公度方法，然后由此并结合多属性价值理论给出能克服DIS-AHP、ABS-AHP、IDE- AHP和SUP-AHP内在方法缺陷的新层次分析方法。由于其中依赖的多属性决策属性价值公度方法要以目标参照方案为基础，因此我们将之称为目标导向层次分析方法(简记为ToAHP)。

2 知识基础与相关评析

(1)多属性价值理论与SW判断

设简单多属性决策问题的决策目标为C，其所涉及的属性(指标)有n个，依次记为C1,…,Cn；备选决策方案集为{A|A=(x1,…,xn)}，其中x1,…,xn分别是方案A在属性C1,…,Cn上的属性值，xi∈Ri(Ri为决策方案A在属性Ci上的属性值取值范围)，i=1,…,n。

基于von Winterfeldt和Edwards[23]，我们有如下定义1：

(1)

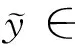
当V(Ci,A)解释为方案A在属性Ci上的满意度(又称为偏好强度)并按区间量制予以测度时，由式(1)确定出的V(C,A)称为属性偏好绝对独立条件下方案A在属性C1,…,Cn上的多属性综合价值，V(Ci,A)相应地称为方案A在属性Ci上的价值(或方案A在属性Ci上的属性值xi的价值)[23]。

von Winterfeldt和Edwards[23]为保证属性权重具有合理的内涵解释，给出了关于属性权重判断与赋值的SW方法。当C1,…,Cn均为正向属性(即属性值越大决策者对其偏好也越大的属性)、决策方案个数为Q时，其具体步骤为：首先，定义两个锚点方案即虚拟最差方案AD和虚拟最好方案AH，其中，

AD=(x1,D,…,xn,D)，AH=(x1,H,…,xn,H)

xi,D=minq{xi,q|q=1,…,Q}

xi,H=maxq{xi,q|q=1,…,Q}

然后，让决策者关于Vi,H-Vi,D和Vf,H-Vf,D进行偏好比率判断，其中，Vf,H-Vf,D为决策者希望首先在第f(f∈{1,…,n})属性上将AD的属性值改进为AH的属性值所带来的偏好(满意度)变化；Vi,H-Vi,D为决策者在第i(i=1,…,n)属性上将AD的属性值改进为AH的属性值所带来的偏好(满意度)变化。设决策者关于Vi,H-Vi,D和Vf,H-Vf,D判断给出的偏好比率为βi,f，i=1,…,n，则属性Ci的权重(称为SW权重)为：

(2)

虽然SW判断也是比率判断，但它与AHP的两两比较相对重要性判断不同，拥有着明确的判断基准“0”点——判断βi,f的基准“0”点(参考点)为Vi,*=Vi,D时的Vi,*-Vi,D(或换言之xi,D为参考点并由此从多个属性上讲AD是SW判断的参考点)[23]。此外，von Winterfeldt和Edwards[23]认为只有当xi,D，xi,H具有具体计量单位或客观分类标准时，决策者才能进行SW判断，因此决策方案在属性C1,…,Cn上具有具体计量单位或客观分类标准是决策者能够进行SW判断的前提条件。

(2)DIS-AHP与SUP-AHP

DIS-AHP包含如下四个分析步骤[1-3]。

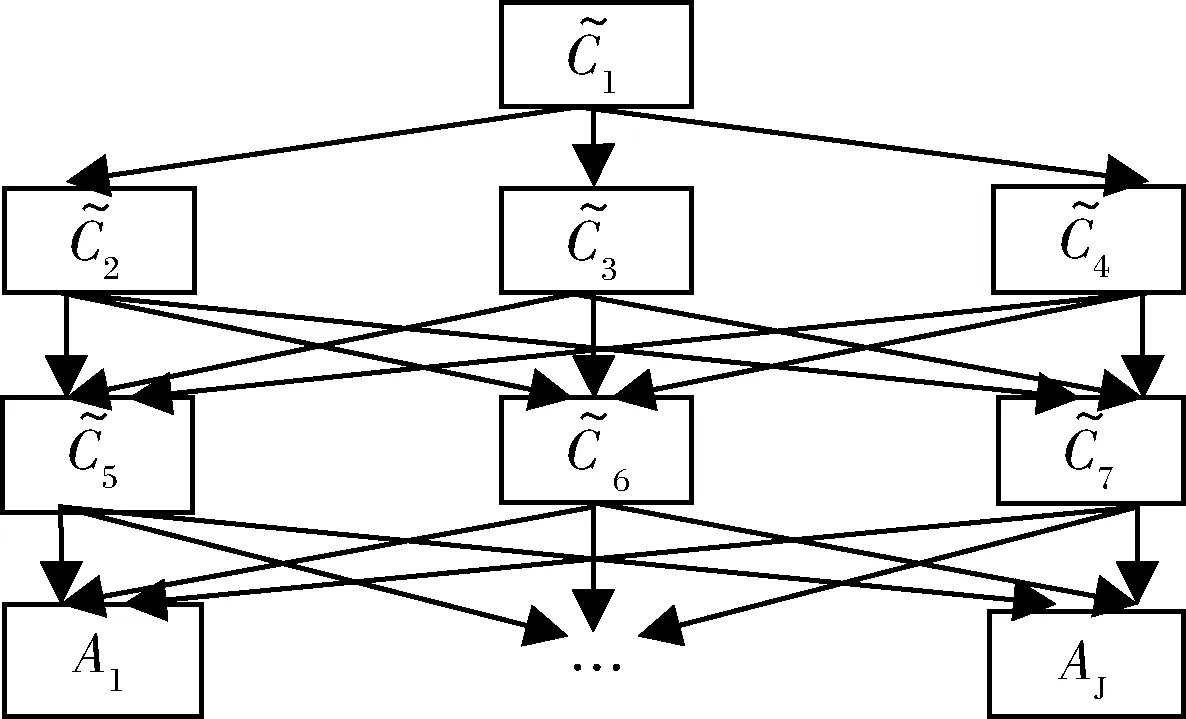
图1 DIS-AHP层次分析结构

步骤2：构建层次判断矩阵。以每个非方案层元素为准则，让决策者将与之相联系的所有下层元素进行两两相对重要性比较，并用9级比率标度对比较结果予以赋值，构建出层次判断矩阵。

步骤3：基于层次判断矩阵计算层次单排序权重并对层次判断矩阵进行逻辑一致性检验。其中，层次单排序权重是指同一层次各个因素相对于上一层次某个与它们有箭线联系的因素的权重。

步骤4：基于层次单排序权重计算方案层各个方案的复合排序权重，并以此进行方案优选。

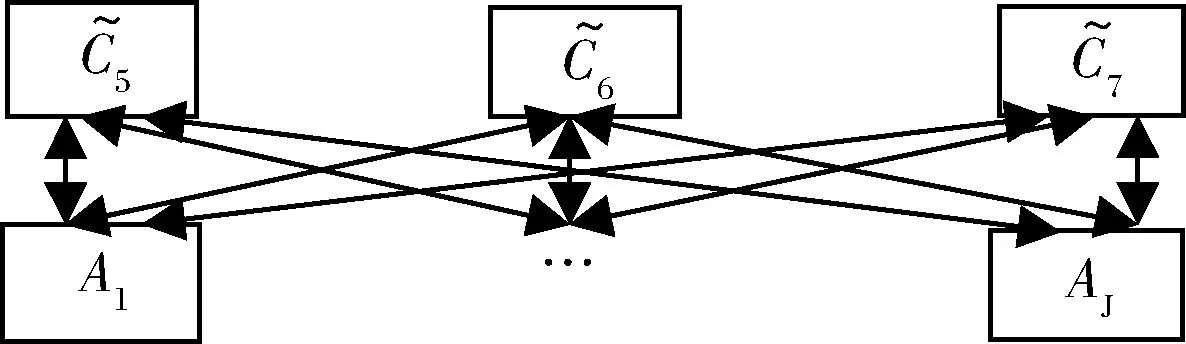
图2 SUP-AHP层次分析结构

则SUP-AHP在引入正整数η后要求按照[limη→+∞Q1(Q2Q1)η](1,0,0)T得出A1,…,AJ的最终优劣排序权重向量(即综合评价值向量)[3，12]。

若只从权重处理能否合理规避方案评价逆序而不考虑比较判断难以实施问题，SUP-AHP要比DIS-AHP以及ABS-AHP、IDE-AHP更具有可信性[12]。针对SUP-AHP相对方案比较判断底层属性权重所出现的难以判断问题，Leung和Cao Dong[12]以“方案的总价值(即综合评价值)是方案在各个底层属性上所展示出来的价值之和”为依据，将底层属性相对于方案的权重解释为方案在底层属性上所展示出来的价值占方案总价值的比例。但需要强调指出，虽然Leung和Cao Dong[12]关于SUP-AHP给出了上述内涵解释，但这并不意味着在实际应用SUP-AHP时决策者就能够基于该内涵解释进行相对于方案的底层属性相对重要性判断。其中原因在于：决策者若能够进行判断，则至少须首先知道方案的总价值(综合评价值)，而这与应用SUP-AHP的目的即给出方案的综合评价值形成了悖论性的逻辑反复。

(3)多属性决策属性价值公度方法

F0,i(xi,(mi)|πi)=p(xi,(1))+…+p(xi,(mi))

(3)

由F0,i(xi,(mi)|πi)可知：属性值xi∈[xi,1,+∞)对应参照分布πi的累计概率为：

Fi(xi|πi)=

(4)

李春好等[24]在融合累积前景理论(Cumulative Prospect Theory—CPT)[25]价值函数、范围—频率理论(Range-Frequency Theory)[26]价值函数之上，基于DEA和马尔可夫链(Markov Chains)给出了如下多属性决策属性价值公度方法：

(5)

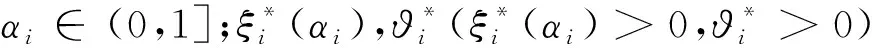
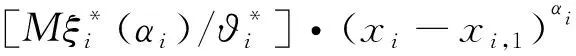
需要指出，上述属性价值公度方法在决策应用时，需要事先基于大量繁琐前景(由多个属性值及其对应概率构成)等价判断实验拟合出参数αi的取值，因而从实际决策上讲存在着适用性不强问题。

3 基于SW判断的规约性多属性决策属性价值公度方法

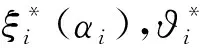
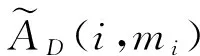
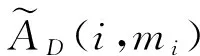
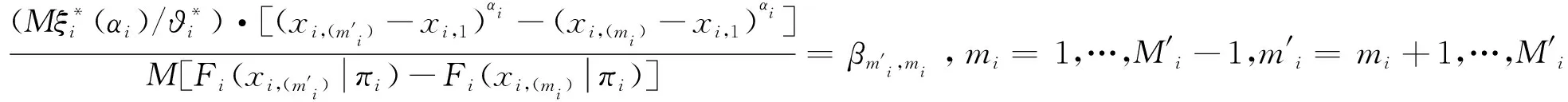
(6)

(7)

(8)

(9)

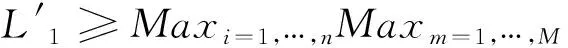
4 支持ToAHP构建的定义与定理

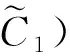
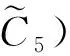
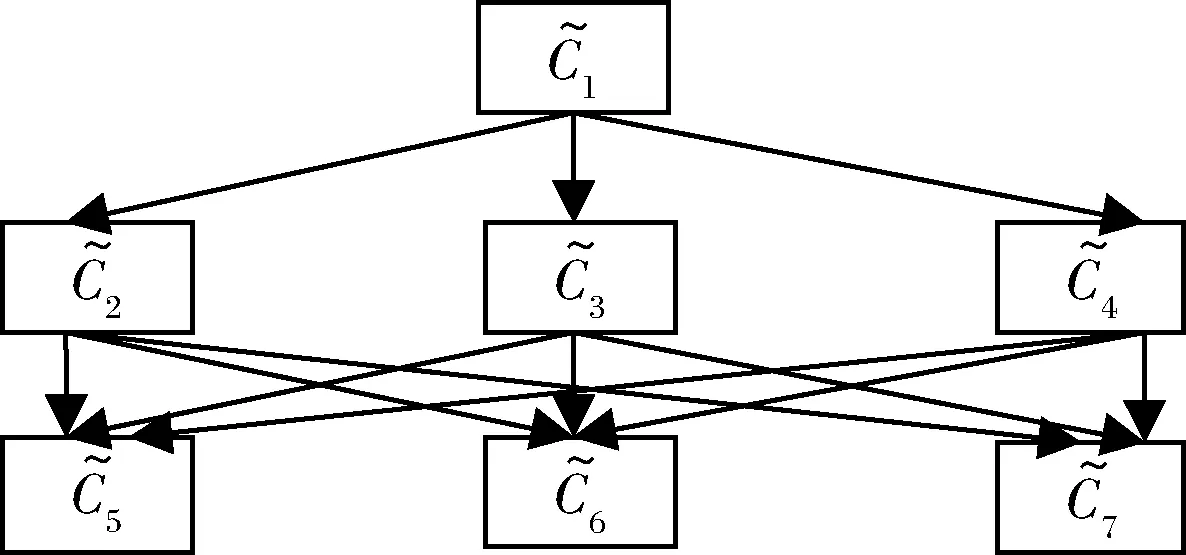
图3 属性层次结构

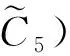
定义5：若属性层次结构中任一属性的各个紧密下层属性之间呈现属性偏好绝对独立关系，则称该层次结构为偏好绝对独立属性层次结构。

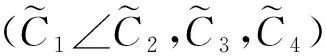
由于一个简单结构层次中上层属性体现为简单多属性决策问题的目标，下层属性体现为简单多属性决策问题的指标，因此基于偏好独立应用多属性价值理论可知：一个决策方案在偏好绝对独立简单结构层次的上层属性上的价值是决策方案在下层属性上的属性价值的加权和，并且其中与各个下层属性相联系的权重相对于方案的变化固定不变。由此并为后文叙述方便，我们给出下述定义7。

定义7：对于一个偏好绝对独立简单结构层次而言，反映上层属性与各个下层属性之间价值联系的权重，称为下层属性相对于上层属性的单排序权重(简称为层次单排序权重)。

由于一个属性(因素)上的价值函数的任意正线性变换仍是该属性的价值函数，因此一组决策方案在一个属性上的价值(偏好强度)可以采用任意一个区间量制予以测度。由此可知：一组决策方案在一个属性层次分析结构各个属性(因素)上的价值测度既可以采用彼此不同的区间量制也可以采用同一个区间量制。这里我们感兴趣的是让决策者采用同一个区间量制[0,b]来测度一组决策方案在属性层次分析结构各个属性(因素)上的价值。为此，我们给出如下定理与推论。

定理1：对于一个偏好绝对独立属性层次结构而言，若决策者对一组决策方案在某个次底层属性的紧密下层属性(部分或全部具体属性)上的价值(偏好强度)均按同一个区间量制[0,b]来测度，并且对于该次底层属性与其紧密下层属性所构成的偏好绝对简单结构层次而言层次单排序权重之和为1，则决策者对该组决策方案在该次底层属性上的价值测度采用的是区间量制[0,b]。

0=V5(ALT1)≤V5(A)≤V5(ALT2)=b

0=V6(ALT1)≤V6(A)≤V6(ALT2)=b

0=V7(ALT1)≤V7(A)≤V7(ALT2)=b

V2(ALT1)=τ2,5V5(ALT1)+τ2,6V6(ALT1)+τ2,7V7(ALT1)=0

V2(ALT2)=τ2,5V5(ALT2)+τ2,6V6(ALT2)+τ2,7V7(ALT2)=b

V2(A)=τ2,5V5(A)+τ2,6V6(A)+τ2,7V7(A)

由定理1，可以给出下述重要推论。

推论1：对于一个偏好绝对独立属性层次结构而言，若决策者对一组决策方案在所有具体属性上的价值均按同一个区间量制[0,b]来测度，并且对于任意一个偏好绝对独立简单结构层次而言层次单排序权重之和均规定为1，则决策者对该组决策方案在任一属性(非具体属性)上的价值测度采用的也是区间量制[0,b]。

证明：仿照定理1的证明过程对偏好绝对独立属性层次结构自下而上地对每个属性上的区间量制进行递推，即可得证。[证毕]

5 价值测度量制[0,b]的界定与层次单排序权重的判断赋值

由推论1可知：要在一个偏好绝对独立属性层次结构的所有属性上实现按同一个区间量制[0,b]测度决策方案的属性价值，则必须在层次结构的每个具体属性上均采用同一个区间量制[0,b]测度决策方案的属性价值。由此并考虑到前文给出的规约性属性价值公度方法，这里建议分别针对偏好绝对独立层次结构中的每个具体属性应用该方法并将由此得出的价值公度区间[0,L′]视为区间量制[0,b](下文将由此界定出的区间量制称为价值公度区间量制[0,b])。

下面基于最受学术界推崇的SW判断模式并结合属性价值公度区间量制[0,b]，给出能够适用于偏好绝对独立属性层次结构中每个简单结构层次的层次单排序权重判断与赋值方法。

不失一般性，假设偏好绝对独立属性层次结构如图3所示。由此构造如下两个虚假锚点方案：

ALT*(1)=(50,60,70)

ALT*(2)=(5b,6b,7b)

s,s′=5,6,7;s≠s′

(10)

τ2,s=η2:s,7/(η2:5,7+η2:6,7+1),s=5,6,7

(11)

基于τ2,5,τ2,6,τ2,7和(50,60,70)、(5b,6b,7b)两向量，由的偏好绝对独立性和推论1易知：ALT*(1)和ALT*(2)在属性上基于价值公度区间量制[0,b]的属性价值分别为

V2(ALT*(1))=τ2,5·0+τ2,6·0+τ2,7·0=0(个)

V2(ALT*(2))=τ2,5·b+τ2,6·b+τ2,7·b=b(个)

V3(ALT*(1))=0(个)

V3(ALT*(2))=b(个)

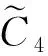
V4(ALT*(1))=0(个)

V4(ALT*(2))=b(个)

基于上述计算结果，可以将ALT*(1)和ALT*(2)分别重新表示为：

ALT*(1)=(20,30,40)

ALT*(2)=(2b,3b,4b)

6 目标导向层次分析的方法程序

(12)

(13)

(14)

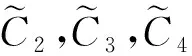
V2(Aj)=τ2,5V5(Aj)+τ2,6V6(Aj)+

τ2,7V7(Aj)

V3(Aj)=τ3,5V5(Aj)+τ3,6V6(Aj)+

τ3,7V7(Aj)

V4(Aj)=τ4,5V5(Aj)+τ4,6V6(Aj)+

τ4,7V7(Aj)

V1(Aj)=τ1,2V2(Aj)+τ1,3V3(Aj)+

τ1,4V4(Aj)

将V2(Aj)、V3(Aj)和V4(Aj)带入到上式可得：

V1(Aj)=(τ1,2τ2,5+τ1,3τ3,5+τ1,4τ4,5)V5(Aj)+(τ1,2τ2,6+τ1,3τ3,6+τ1,4τ4,6)V6(Aj)+(τ1,2τ2,7+τ1,3τ3,7+τ1,4τ4,7)V7(Aj)

(15)

以图3所示的偏好绝对独立属性层次结构为例，基于式(15)可给出如下目标导向层次分析方法(ToAHP)的具体步骤。

步骤1：基于层次结构所有具体属性定义备选决策方案Aj=(xR⊥j,5,xR⊥j,6,xR⊥j,7)，j=1,…,J。

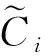
步骤3：基于公度区间量制[0,b]和SW判断得出每个简单结构层次的层次单排序权重即τ2,5,τ2,6,τ2,7；τ3,5,τ3,6,τ3,7；τ4,5,τ4,6,τ4,7；τ1,2,τ1,3,τ1,4。

7 ToAHP相对于AHP的方法优势

(1)权重判断模式与权重内涵。ToAHP在每个简单结构层次上关于层次单排序权重采用的均是多属性价值理论中最受学术界推崇的SW判断模式，由此得出的层次单排序权重因存在判断的参考点(即虚拟最差方案)而具有清晰的概念内涵即对应属性上公度价值变化的偏好当量系数。与此不同，AHP在DIS-AHP、ABS-AHP和IDE-AHP三种具体方法中关于层次单排序权重采用的是脱离方案变化以及属性价值变化、并没有判断参考点的相对重要性判断，由其得出的排序权重因而在学术界饱受争议并被认为存在内涵模糊不清问题。而AHP在SUP-AHP中除类似DIS-AHP、ABS-AHP和IDE-AHP采用了相对于底层属性比较方案的相对重要性判断，还引入了相对于方案比较底层属性的相对重要性判断，由此得出的底层属性权重在内涵上要比由相对于底层属性比较方案的相对重要性判断所得出的层次单排序权重更加不清晰。

(2)方法建构的理论基础与决策者偏好结构的检验。在具有具体计量单位的属性价值公度区间量制的支持下，ToAHP实际上是将复杂层次化决策按照自下而上的层次次序转化成了一系列简单多属性决策，其建构的理论基础是基于偏好强度区间量制、拥有健壮定理系统支持的多属性价值理论，因此能够根据决策者行为描述对其中采用的偏好结构(即偏好绝对独立)进行适用性检验。与此不同，AHP依赖的是具有独特规定性质的、内涵模糊的相对量制，尽管Saaty基于该相对量制给出了AHP的基本原理，但Dyer等认为这些原理与效用理论、价值理论不同，仅是心理学意义上的原生性看法，因此AHP假定的层次分解原则(即单层次属性相对于上层属性偏好绝对独立)并不能根据决策者的行为描述予以方法是否适用的事前检验[4,7]。

(3)保序能力与其内在数理依据。由于DIS- AHP不具有方案评价的保序能力，而SUP-AHP虽具有方案评价的保序能力，但因无法逾越相对方案比较底层属性权重的难题而缺乏实际应用的可操作性，因此这里仅对AHP的另外两种分析方法(即ABS-AHP和IDE-AHP)和ToAHP予以对比分析。由ToAHP、ABS-AHP和IDE-AHP的决策分析过程易知，即使在备选决策方案集中引入与较差方案完全相同的无关复制方案，它们针对其它方案均具有方案评价的保序能力，都不会出现逆序问题。但是，从所给出的、决定方案优劣排序的方案综合评价值的内在数理逻辑上讲，它们却有着明显区别。结合式(10)和式(11)可以看出，ToAHP确定层次单排序权重的SW判断虽与b的取值大小无关，但必须依赖b的具体计量单位即战胜或战平目标参照方案的数目“个”，因此从根源上讲依赖于具体属性上的价值公度区间量制[0,b]即[0,L′]。另一方面，从规约性属性价值公度方法以及式(12)上看，[0,L′]和决策方案在具体属性上的公度价值均依赖于所有目标参照方案。综合上述两方面可知：如果将所有目标参照方案视为决策者选定的评价标准体系，那么ToAHP的层次单排序权重和决策方案在具体属性上的公度价值均是源于同一个评价标准体系而予以确定的，因此在给出方案综合评价值时无需考虑评价标准体系是否协调问题。与此不同，ABS-AHP和IDE-AHP在层次结构底层属性上要求决策者基于经验对决策方案进行价值评分，但在属性层次单排序权重的确定上所依赖的均是内涵模糊不清的相对重要性判断，人们并不能理清其中依赖的究竟是什么评价标准体系，这样便无法保证所给出的层次单排序权重和决策方案在底层属性上的价值评分均源于同一个评价标准体系。另一方面，ABS-AHP和IDE-AHP基于层次单排序权重和决策方案在底层属性上的价值评分确定决策方案综合评价值时，并没有考虑评价标准体系是否协调以及如何协调问题(事实上因相关内涵模糊不清也无法考虑这类问题)。综上所述并与ToAHP相比较可知，在给出决策方案综合评价值的数理依据上，ABS-AHP和IDE-AHP明显弱于ToAHP。

8 应用对比分析

由于在不考虑AHP权重判断的内涵模糊不清问题以及由此带来的判断可操作性差问题的条件下，SUP-AHP是能够基于可靠数理依据规避方案评价逆序问题、要比AHP的其它三种分析方法更具可信性的一种分析方法[12]，因此，这里仅进行ToAHP与SUP-AHP的应用对比分析。

考虑到应用SUP-AHP时要出现相对方案比较判断底层属性权重(其内涵要比AHP属性权重更加模糊不清)而事实上从可操作性上看又难以判断的问题，同时也是出于满足方法比较输入信息可比这一基本要求上的考虑，下文先开展ToAHP的应用，然后以此应用所提供的基本信息为基础，按照SUP-AHP的相关要点构造给出方法应用的输入信息(其实质是假设决策者能够克服上述判断难题给出底层属性相对于不同方案的权重)，最后对ToAHP和SUP-AHP进行应用对比分析。需要指出，下文在方法应用中所使用的属性层次结构仅是一个为控制论文篇幅、使方法对比分析更为简洁的分析结构，它相对于具体实际决策所应采用的多视角多层面分析结构而言只是一个简化版本。

图4 教师工作绩效评价的属性层次结构

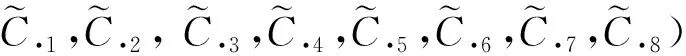
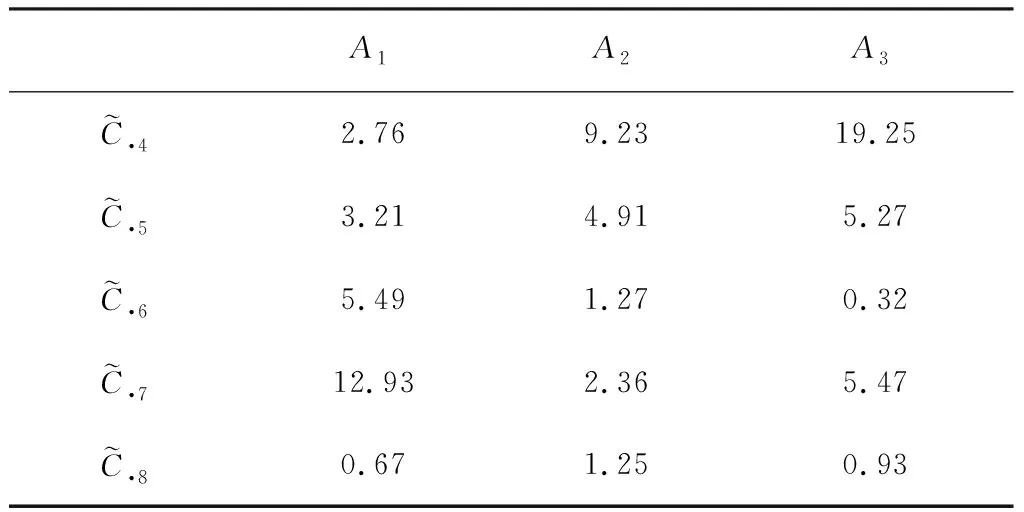
表1 决策方案在具体属性上的公度价值(单位：个)

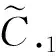
V·1(A1)=0.36×2.76+…+0.09×0.67=5.68(个)

V·1(A2)=0.36×9.23+…+0.09×1.25=4.81(个)

V·1(A3)=0.36×19.25+…+0.09×0.93=9.02(个)

基于Q1和Q2，由SUP-AHP可得A1,A2,A3的综合评价值向量：(0.2913,0.2464, 0.4623)。

比较上述分别由ToAHP和SUP-AHP对A1,A2,A3所给出的综合评价值(向量)可知：[V·1(A1),V·1(A2),V·1(A3)]=19.51·(0.2913, 0.2464, 0.4623)。它表明：在输入信息假设可比的条件下，ToAHP在方案排序和方案相对优劣程度两个方面上，能够给出与AHP四种分析方法中权重处理最具可信性的SUP- AHP完全一致的评价结论。由此并结合ToAHP和SUP-AHP在权重判断可行性上的差异(即ToAHP依赖的是易于实施的SW判断模式而SUP-AHP依赖的是可操作性差、难以实施的相对重要性判断模式)可知，ToAHP明显优于SUP-AHP。

9 结语

为发展AHP，上文基于拥有健壮多属性价值理论基础的SW判断和多属性决策属性价值公度方法，给出了能够为层次结构抽象属性上SW判断提供支持的规约性属性价值公度方法，并在此基础上结合多属性价值理论给出了目标导向层次分析方法(即ToAHP)的价值测度量制、层次单排序权重判断模式和决策分析步骤。ToAHP在三方面克服了AHP(包括DIS-AHP、ABS-AHP、IDE-AHP和SUP-AHP)的内在缺陷。其一，在规约性属性价值公度方法的支持下，其依赖的权重判断模式(即SW判断)对所有抽象属性而言均存在明确的判断参考点，因而能够保证属性权重具有清晰的概念内涵。其二，拥有可靠的多属性价值理论基础，因此能够基于决策者行为描述来判别其在具体决策应用时的方法适用性(即偏好绝对独立是否满足)。其三，能够实现方案评价保序，并在方案评价保序上拥有科学合理的内在数理依据。应用对比分析表明：在输入判断信息假定可比的条件下，ToAHP能够在方案排序和方案相对优劣程度两个方面，给出与SUP-AHP完全一致的评价结论，但由于前者在给出判断信息的可行性上远远高于后者，因而从综合比较上讲其科学合理性明显优于后者。需要指出，ToAHP与迄今已得到广泛应用的传统多属性价值决策模型一样，均以偏好绝对独立为决策应用的适用条件，因此严格说来决策分析者在具体决策应用时，应针对每个简单结构层次检验决策者的行为描述是否满足偏好绝对独立假设。此外，如同学术界为弱化传统多属性价值决策模型的偏好绝对独立假设而提出能够适用于更广泛决策场合的偏好序依赖多属性决策模型(如Choquet积分模型)，未来可从偏好序依赖视角对ToAHP予以进一步发展。