改进区间可接受度的证券投资组合区间二次规划模型
2018-10-16王建建吴子轩陈丽莉
王建建,何 枫,吴子轩,陈丽莉
(1.北京科技大学东凌经济管理学院,北京 100083;2.清华大学经济管理学院,北京 100084)
1 引言
Markowitz[1]在其所提出的M-V模型中,首次运用数理统计方法定量分析了投资组合中风险与收益之间的内在关系。该理论开辟了金融定量分析的时代,为现代证券投资组合理论奠定了坚实的基础,并由此衍生出一系列的相关研究。例如,张鹏等[2]考虑交易成本,借款约束和阈值约束,提出了具有最小交易量限制的多阶段均值-半方差投资组合模型。该模型与已有的多阶段投资组合相比,所研究的多阶段投资组合之决策变量是整数,该特点符合现实投资组合。周忠宝等[3]则构建了考虑交易成本的多阶段投资组合优化模型,其基于真实前沿面定义了投资组合的效率并提出了相应的非线性模型进行计算求解。张鹏等[2]和周忠宝等[3]虽然考虑了交易量及交易成本,但它们研究的均是确定性条件下的证券投资组合模型。
然而,在现实的证券市场中,诸多不确定因素的存在使得预期收益、风险损失率以及市场流动性(比如以换手率刻画)具有动态性[4];对此,投资者很难给出精确的数值。因此,在实践中,投资者只能获取证券收益率、风险损失率及换手率的变化范围,并通常以区间数来表示此类问题,也即引申出所谓的区间规划问题。目前,区间规划问题已成为研究投资组合的热点问题之一。综上,本文认为对投资收益及风险等为区间数的投资组合区间规划模型展开研究,不仅可以完善和丰富不确定的优化理论,对其恰当的应用也有助于投资者在实际证券市场中进行更加合理的投资选择。
证券投资组合的区间线性规划问题研究虽有不少,但其方法却相对简单。例如,Tong Shaocheng[5]针对目标函数系数和约束系数为区间数的情况,给出了目标函数值范围。Lai等[6]讨论了目标函数和约束条件为区间数的问题,以区间数来描述收益率在证券市场的不确定性,提出了半绝对偏差度量风险的投资组合模型,并将其转化为线性区间规划模型进行求解。Wu Meng等[7]提出了收益和风险均为区间数的证券投资组合模型,通过使用区间数和凸分析,得到非劣解。陈华友和赵玉梅[8]等通过引入区间数线性规划问题中的目标函数优化水平α和约束水平β,提出了证券组合投资的区间数线性规划模型。赵玉梅等[9]给出了一个考虑交易费用的证券组合投资的区间数线性规划模型,具体是通过引入区间数线性规划问题中的目标函数优化水平参数和约束条件满足水平参数,将区间数线性规划模型转化为确定型的一般线性规划模型进行求解。一般而言,在证券投资组合的非线性规划问题中,二次规划是一类特殊的非线性规划。目前,关于区间二次规划的求解方法有:Liu和Wang[10]研究了目标函数线性部分及约束条件中含有区间数的二次规划问题的求解。在此基础上,Li Wei等[11]针对弱条件下的区间二次规划问题,进一步提出了一种新的方法来计算上界的最优值,并讨论了新方法和传统方法的关系。徐晓宁等[12-13]则针对市场不允许卖空和允许卖空两种情况提出了基于区间数排序方法的区间二次规划模型;但是该模型未考虑交易成本及市场流动性的影响,这使得所建立的模型仍不够贴近实际的投资活动,具有一定的局限性。
综上来看,目前关于证券投资组合区间二次规划的求解方法较少且仍有不少拓展空间。本文在均值方差模型的基础上,拟引入交易成本、流动性作为新的约束条件,及使用区间数来更加现实地描述证券的收益率、风险损失率以及流动性,由此建立新的含交易成本的证券投资组合区间二次规划模型。进一步地,本文在此基础上,拟提出改进区间数可接受度的方法,将不确定型模型转化为确定型模型进行求解,这可有利于投资者根据自己的偏好选择相应投资方案。最后,笔者通过证券实例进行验证,以观察本文所建立的模型是否更符合实际的投资环境和具有可行性。
2 区间数理论知识
1) 区间数的相关定义[14]
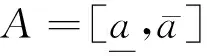
2) 区间数的运算[15]

3 含交易成本的区间二次规划模型
流动性是研究中最主要的问题之一,但实践中具体描述证券未来的流动性却也十分困难。在市场流动性的影响因素方面,大多数学者认为流动性包括宽度、深度、及时性和弹性等四个主要方面。沿用陈国华[16]等研究,本文选择以换手率度量流动性,同时将交易成本设计为线性函数来建立模型。另外鉴于我国证券市场目前大多数暂不不允许卖空,即投资比例满足非负性。最后,我们假设投资者在n种证券之间进行选择。其选择依据是,根据均值—方差模型,投资者将在既定的收益、换手率约束条件下,使得投资组合的风险最小。
综上,可建立含有交易成本的证券组合投资的区间二次规划模型(1):
(1)

3.1 基于α优化水平目标函数的转换
定义3 若x=(x1,x2,…,xn)T满足(1)中的所有约束条件,则称为模型(1)的可行解。由所有可行解构成的集合则称为模型(1)的可行域,记为S。


minf(x)=〈m(f(x)),w(f(x))〉
(2)

minf(x)=(1-α)m(f(x))+αw(f(x))
(3)
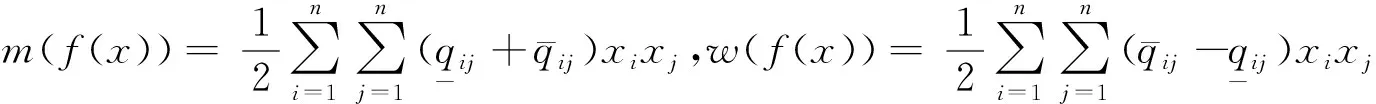
(4)

3.2 基于改进区间可接受度的不确定约束的转换
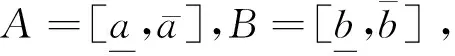
定义7[18]区间的序关系≤MW:
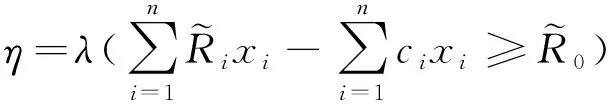
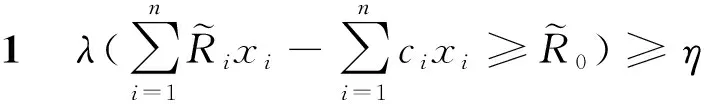
可转化为确定性的约束条件:

证明:(1) 必要性.
根据定义7中的区间序关系≤MW,易得:


经整理可得:

(2)充分性.


整理得:

综上可得:

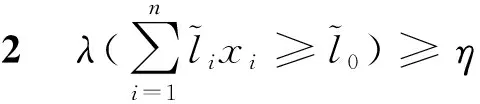
证明方法同定理1,此处省略。
通过引入约束条件可接受水平η,本文提出定义8及结合定义7,提出了改进的区间可接受度的不确定约束转换的定理1和定理2,并给出证明。然后,根据定理1和定理2,将含有区间数的不确定约束条件的二次规划模型(4)转化为确定性的含有交易成本的单目标二次规划模型(5):
(5)
其中,0≤α,η≤1。由本文建立的模型(5)可知,给定α,η不同取值,投资者可获得不同投资组合方案。从这个角度来看,本文的模型适用性更强,这说明,对于模型(1)的求解,基于改进的区间可接受度的确定型转化方法与传统确定型转化方法相比,本文的方法更具优势。
3.3 含交易成本的区间二次规划的另一数值解法
目前,已有许多关于区间数线性规划的求解方法。例如,郭均鹏和李汶华[19]提出了最好最优值和最差最优值,以及最大范围不等式和最小范围不等式的定义,将区间线性规划问题转化成确定性的规划问题进行求解。对于含交易成本的证券投资组合区间二次规划模型(1),采用郭均鹏和李汶华[19]的方法,可将含交易成本的区间二次规划模型(1)转化成两个确定性的二次规划模型(6)和(7)进行求解。通过求解模型(6)和(7)的最优解,可得含有交易成本的证券组合投资的区间二次规划模型(1)的目标函数的上下界,根据上下界来确定投资组合的最小风险区间。
(6)
(7)
4 数值算例
本文沿用邓雪等[20]中的数据,假设投资者要将资产分配至3种证券,分别为:东方集团、上汽集团、五矿发展的2005年4月至2009年3月的每月收盘价及换手率,并可计算这三种证券对应的期望收益率区间、方差及协方差风险区间以及换手率区间分别如下:
期望收益率区间:
方差及协方差风险区间:
换手率区间:

4.1 基于改进的区间可接受度的解法
基于以上数据,本文应用MATLAB软件,可计算模型(5),根据不同的目标函数优化水平α和约束条件的可接受水平η,以及设置α、η不同的取值,可得到不同的投资组合的方案。由此,解得3种证券投资组合的投资比例及风险值如表1所示。
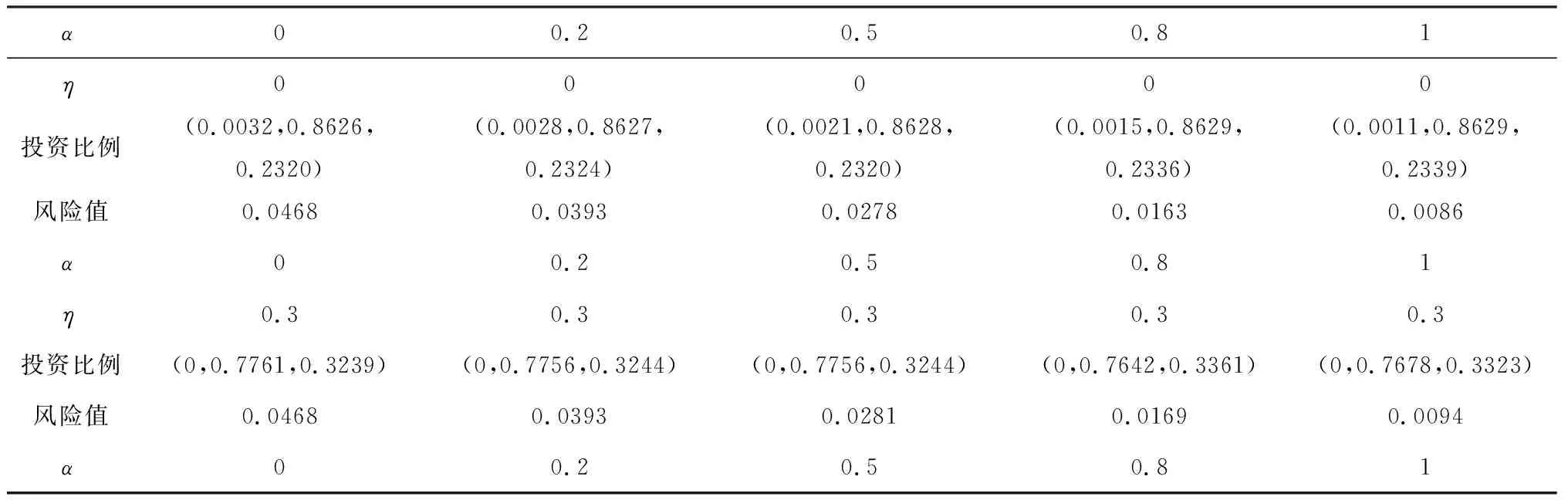
表1 基于不同优化水平及可接受水平的投资组合比例

续表1 基于不同优化水平及可接受水平的投资组合比例
由上表可知:固定η值,投资者选择的目标函数优化水平α越大,则投资者投资风险就不断减小;相反,则越大。固定α值,投资者给出的约束条件可接受水平η越大,即投资者对于期望收益率以及换手率的可接受度越来越大,则投资者所要承受的风险也将不断增大;相反,则越小。这符合证券投资组合理论中“高收益伴随高风险”的实际情况,也表明该模型具有较好的实际意义。由表1可得出,目标函数风险值的范围,即风险区间为f(x)=[0.0086,0.0509]。
固定η=0,由图1可看出,目标函数值即证券投资风险值随优化水平α的增加而减小,在α∈[0,1]内,目标函数值随优化水平α呈现单调递减情况。图1则更加直观地反映了投资者优化水平α变化时风险值的变化情况。

图1 证券投资风险值随优化水平α的变化
固定α=0.5,由图2可得,总体上目标函数值即证券投资风险值随约束条件可接受水平η值的增加而呈上升趋势。当η∈[0,0.7]时,随约束条件可接受水平η值的增加,目标函数值逐渐增大,增长趋势较慢;当η∈[0.7,0.9]随约束条件可接受水平η值的增加,目标函数值快速增大。当η∈[0.9,1]时,随约束条件可接受水平η值的增加,目标函数值增长趋势逐渐放缓。图2直观地反映了投资者可接受水平η值变化时风险值的变化情况。
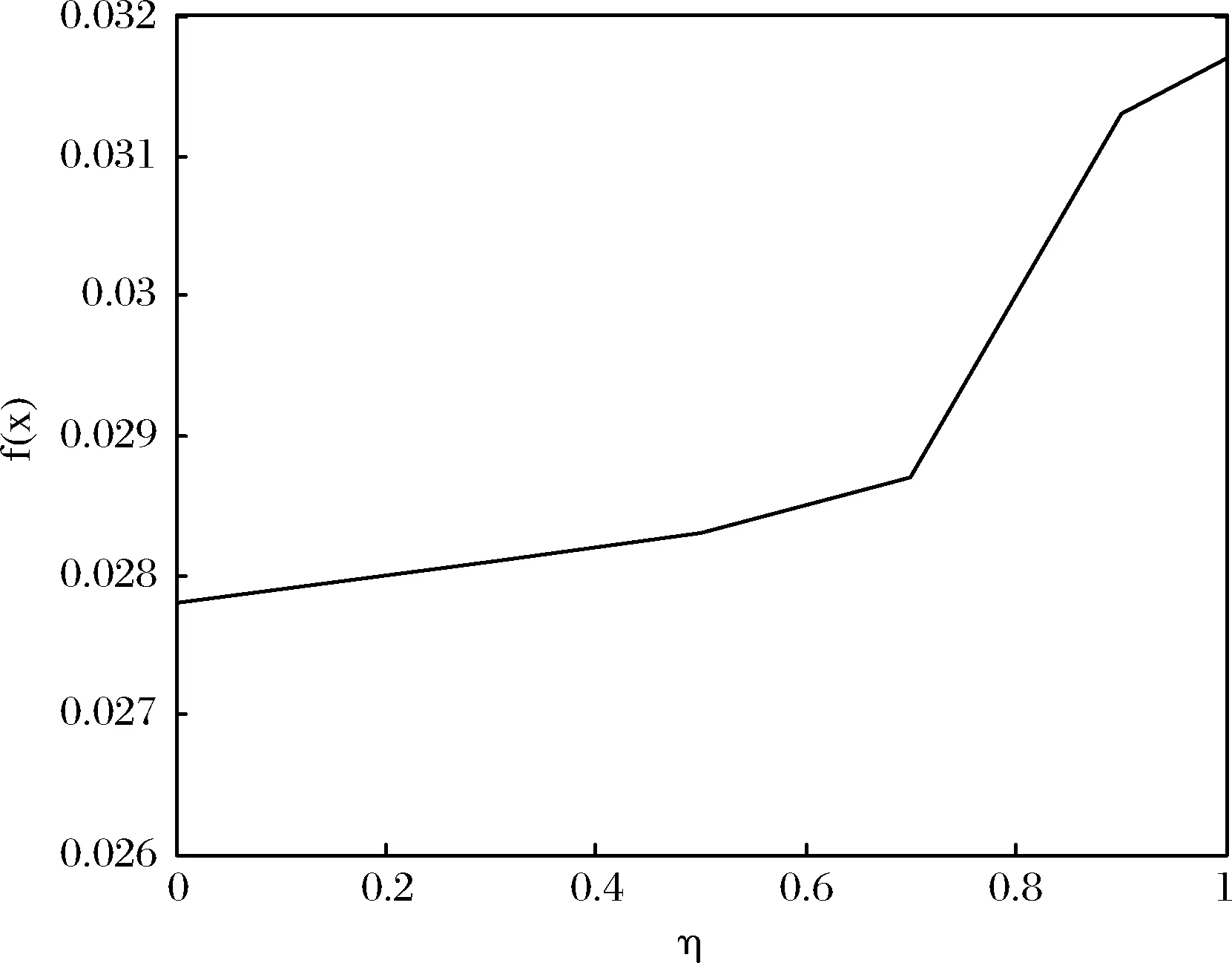
图2 证券投资风险值随可接受水平η的变化
4.2 另一区间二次规划的数值解法
根据本文4.1节数据,可分别求解3.3节中的模型(6)和(7)。其中,所求最优解分别表示为模型(1)目标函数的上、下界值,其结果如下:
目标函数的下界:x=(0.2441,0.4627,0.2933),fL(x)=0.0285
目标函数的上界:x=(0,0.0749,0.9251),fU(x)=0.0567
从而得到含有交易成本的证券投资组合二次规划模型的解区间为f(x)=[0.0285,0.0567]。
4.3 两种解法的比较
将两种方法求得的证券投资组合模型的目标函数值分别表示为:f1=[0.0086,0.0509],f2=[0.0285,0.0567]。这两个区间的位置关系如图3所示:

图3 两个区间数的位置关系
由图3及文献给出的区间序关系以及区间可能度的定义,可得出f1,f2是相交的却不包含。根据Ishibuchi和Tanaka[18]确定性的区间序关系≤MW比较f1和f2,由于m(f1)=0.0298 通过区间数确定性序关系的排序方法及区间可能度的比较,我们发现,在求解含有交易成本的证券投资组合区间二次规划模型(1)时,基于本文改进区间可接受度的求解方法明显优于第二种解法。进一步地,应用本文方法,在实践中有利于投资者依据自己偏好来选择具体的投资组合方案以更有效率地配置资产。 考虑到现实证券市场中有很强的不确定性,本文将证券风险、收益以及其相应流动性的不确定性用区间数予以描述,建立了一种新的含交易成本的证券投资组合区间二次规划模型。其次,为求解该模型,本文提出了基于α优化水平转换目标函数,同时也给出了改进的区间可接受度将不确定约束条件转化为确定性含参数的线性约束转换方法。第三,本文采用郭均鹏和李汶华[19]的传统方法给出本文模型的另一数值解法。最后,我们还结合模型给出了具体证券投资算例,分别采用本文的方法以及已有的传统方法对所提出的模型进行求解。数值算例的结果表明,由本文方法所求得目标函数风险值的范围要小于传统方法求得的范围。一般来说,在收益一定的情况下,目标函数的风险范围越小,投资组合的风险就越小,投资就越理性。 我们认为,本文模型为证券投资者提供了一种新的投资思路。基于本文所提出的方法,投资者可依据自己偏好选择具体的投资组合方案,这在实践中具有更好的操作空间。但是,稍有遗憾的是本文仅考虑交易成本为线性函数的情况。因为,现实证券市场中存在着不同形式及不同复杂程度的交易成本,而各种不同形式的交易成本又极有可能影响证券投资组合的选择。因此,在不同形式交易成本的下,关于含交易成本的区间二次规划模型的求解仍有广阔的研究与拓展空间。这也正是笔者未来进一步研究的主要方向。5 结语
