多目标优化算法在弹头侵彻明胶运动模拟中的应用*

莫根林，金永喜，李忠新，吴志林

(1.江苏大学先进制造研究院，江苏 镇江 212013；2.中国兵器工业第208研究所瞬态冲击技术重点实验室，北京 102202；3.南京理工大学机械工程学院，江苏 南京 210094)

为揭示弹头侵彻人体组织的致伤机理，通常采用弹道明胶作为人体组织的替代物[1-2]。程可[3]、S.S.Liu等[4]和Y.Wen等[5]、温垚珂等[6]建立了步枪弹侵彻明胶的数值模拟模型；D.Datoc[7]、Y.Wang等[8]、G.H.Yoon等[9]建立了手枪弹侵彻明胶的数值模拟模型。刘坤等[10]、Liu等[11]基于弹头所受合力和合力矩的经验假设建立了弹头侵彻明胶的平面运动模型；莫根林等[12]基于弹头表面微元的受力假设建立了弹头的六自由弹道模型。研究表明这些模型均能较好地模拟对应投射物的运动规律，但模型中的力学系数和弹头的一些初始运动参数一般不是由实验直接得到的[1]，而是由试算的方法进行推测的。由于待定参数较多，为获得较好的弹头运动模拟结果，试算过程会消耗大量的时间。

待定参数的试算过程可看作是一个多目标问题的求解过程。传统求解此类问题的方法一般是利用线性加权法、约束法等将其转化为单目标问题，但其存在探索未知空间的能力不强、容易陷入局部极值点等问题，不能很好地处理复杂、非线性问题[13]。而多目标进化算法如多目标遗传算法(MOGA)、Pareto存档进化策略(PAES)、非劣分类遗传算法(NSGA)以及基于遗传算法的多目标优化算法(Gamultiobj)等，具有全局性和多向性的优点，可以很好地解决此类问题[14]。为此，本文中以待定参数作为优化变量建立弹头侵彻明胶运动模拟的多目标优化模型，并运用Gamultiobj算法和决策策略对优化变量进行求解分析。

1 弹道模型

建立全局坐标系O′-x′y′z′，其中x′轴平行于明胶块底面，y′轴竖直向上，z′轴指向明胶块内部，如图1所示。在弹头上建立连体坐标系O-xyz，其中z轴和弹轴重合，O点位于弹头的质心位置。采用欧拉角描述弹头的空间姿态，即全局坐标系依次绕z轴旋转ψ(进动角)得到辅助坐标系O′-x″y″z″；再绕x″轴旋转θ(章动角)得到辅助坐标系O′-ξηζ，最后绕ζ轴旋转φ(自转角)即可得到坐标系O-xyz,如图2所示。

根据文献[10]，弹头侵彻明胶过程中所受到的阻力FD、升力FL以及翻滚力矩M的大小可表示为：

(1)

式中：ρ为明胶密度、v为弹头速度、A0为弹头的横截面积；δ为弹头速度方向和弹轴方向的夹角(攻角)；CD0和C1为阻力系数，CL0为升力系数，CM0为弹头的转矩系数。阻力FD方向与弹头速度方向相反，升力FL方向垂直于速度方向且与FD和弹轴共面，翻滚力矩M垂直于FD和FL。

令弹头速度方向余弦为(λ1，λ2，λ3)，则弹头的水平速度分量vz、竖直速度分量vy和侧向速度分量vx可以表示为：

vz=vλ3,vy=vλ2,vx=vλ1

(2)

令弹轴在全局坐标系中的方向余弦为(λ4，λ5，λ6)，可由欧拉角表示为[15]：

λ4=sinθsinψ,λ5=sinθcosψ,λ6=cosθ

(3)

令升力FL的方向余弦为(λ7，λ8，λ9)，翻滚力矩M的方向余弦为(λ10，λ11，λ12)，由定义可知，它们可由弹头速度的方向余弦和弹轴的方向余弦表示：

(4)

λ10=λ2λ6-λ3λ5,λ11=λ3λ4-λ1λ6,λ12=λ1λ5-λ2λ4

(5)

在连体坐标系中，令M的方向余弦为(λ13，λ14，λ15)，它与(λ10，λ11，λ12)的关系可表示为[15]：

(6)

因此，M在连体坐标系中的分量Mx、My和Mz可以表示为：

Mx=Mλ13,My=Mλ14,Mz=Mλ15

(7)

根据推广的欧拉动力学方程，弹头的弹道方程可表示为:

(8)

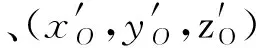
(9)

式中：Jx、Jy和Jz分别为弹头绕x、y、z轴的转动惯量；ωx、ωy和ωz为弹头绕x、y、z轴的角速度分量，它们与欧拉角角速率的关系为：

(10)

将式(1)～(7)和式(9)～(10)带入式(8)，并通过龙格-库塔法求解，可得弹头运动位移和空间欧拉角随时间的变化规律。

2 多目标优化模型与算法

2.1 目标函数组

令弹轴在x′z′平面上的投影与z′轴的夹角(偏航角)为α′、弹轴在y′z′平面上投影与z′轴的夹角(俯仰角)为β′，它们可由弹头的欧拉角计算得到：

tanα′=cosψtanθ, tanβ′=sinψtanθ

(11)

令弹头质心坐标的实验值为(xO，yO，zO)，弹头偏航角的实验值为α，俯仰角的实验值为β。以弹头质心坐标、偏航角和俯仰角的理论值均方根误差表示弹道模型模拟弹头运动的好坏程度，则目标函数组可表示为：

(12)

式中:N为实验数据的总量。

2.2 优化变量

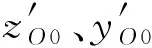
2.3 优化算法

Gamultiobj算法的基本流程如图3所示。初始种群一般由随机产生的多个个体组成，每个个体由待求解的优化变量组成；该算法首先判断初始种群是否满足用户设定条件，若满足则得到Pareto解集(每个解至少存在一个目标值优于集合中所有其他的解)；否则将使种群进化一代，并再一次对其判断，循环往复直至满足终止条件。

种群的进化流程如图4所示。首先，基于个体的序值和拥挤距离，采用锦标赛算法从上一种群(父种群)中选择一定数量的个体，其中序值小的个体先被选中；序值相同时，拥挤距离大的个体被选中。其次对选择得到的个体进行交叉、变异操作，以产生一个由新个体的集合即子种群。其次，将子种群和父种群合并成一个新的种群(此时新种群的大小是父种群的两倍)。最后，通过修剪算法从合并种群中选择与父种群大小相同的新种群，其中修剪算法是基于序值和拥挤距离进行的，序值高、拥挤距离小的个体被剔除[16]。

2.4 决策策略

为从Pareto解集中挑选出最优解，引入TOPSIS综合评价方法对解集中的解进行综合评价[17]。其决策过程可概括为：

(1) 将多目标函数的解构成决策矩阵及规范化决策矩阵；

(2) 确定近似理想解，一般由解集中同一目标的最小值构成；

(3) 求各个解与理想解的近似度。一般首先求出各个解与理想解的距离，其次对多个目标赋予权重，最后将各个权重与各个距离的乘积之和作为近似度；

(4) 根据近似度的大小，对解集中的解进行排序；

(5) 选出最优的多目标函数解[18]。

3 算 例

3.1 实验

实验所用明胶块的制作方法为：将明胶颗粒和水按照1∶9的质量比例混合，并放入水浴炉中加热至60 ℃。保温2 h后将澄清的凝胶液体注入300 mm×300 mm×300 mm的模具中。待模具中的明胶液体冷却至室温时，将其放入4C的恒温箱中保温24 h，经测量其密度为1 060 kg/m3。实验时，以81式7.62 mm自动步枪瞄准明胶块中心位置射击56式7.62 mm普通弹，发射时枪口距离明胶块约2.2 m。实验示意图如图5所示。镜面放置在明胶块上方，明胶块侧面的高速摄像机同时拍摄弹头在明胶块中的运动和弹头在镜面中像的运动。高速摄像机的采样频率为30 000 s-1、曝光时间为2s、图像分辨率为640×480。实验所得弹头侵彻明胶的运动过程如图6所示。通过Phantom Camera Control软件的测量功能从拍摄的图片上测量弹头运动的实验值xO、yO、zO、α和β。

3.2 约束条件

对于弹道模型中的力学系数，在文献[10]的基础上通过试算确定它们的上、下边界,如表1所示。对于弹头的初始运动参数，通过对水平位移zO实验值的差分运算可得vz0=680 m/s，考虑差分误差的影响，限定vz0取值范围为650～730 m/s；由于实验中通过瞄准使弹头的入射方向基本垂直于明胶块的入射面，因此假定弹头速度方向和水平方向的夹角小于3.5。再由vx、vy和vz的关系可知，vx和vy的取值范围均为-30～30 m/s；由图6可知弹头的初始章动角θ0较小，考虑误差的影响，设定其取值范围为-5～5；考虑到弹头轴线方向可能为空间的任意取值，设定弹头进动角ψ0的范围为0～180；由文献[19]可知，弹头出枪口时的自转角速率φt0=1 357 rad/s、进动角速率ψt0=17 997 rad/s，以它们2～3倍的数值估计它们的取值范围,即0<φt0<3 000 rad/s、0<ψt0<40 000 rad/s。由于一般认为弹头的章动角速率θt0较小，设定其取值范围为0～2 000 rad/s。

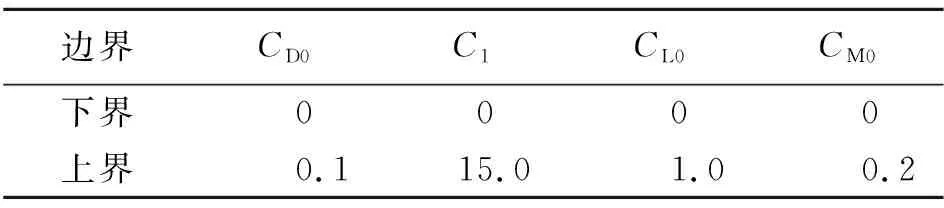
表1 待优化力学系数的取值范围Table 1 Bounds of undetermined mechanical coefficients

3.3 计算结果

设定Gamultiobj算法的具体参数为：种群的大小，200；初始种群的生成，随机法；变异操作，自适应可行策略；交叉操作，中间策略；优化的终止条件，迭代次数达600次或平均适应值函数的相对误差小于0.5×10-4。由于多目标函数组(12)中的各个目标之间相互独立，令TOPSIS算法中各个目标的权重相同均为0.2。

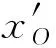
序号C1CD0CL0CM0vx0/(m·s-1)vy0/(m·s-1)vz0/(m·s-1)θ0/(°)ψ0/(°)θt0/(rad·s-1)ψt0/(rad·s-1)φt0/(rad·s-1)17.490.058 60.6360.064 7-22.4-14.207131.91068.81 0201 22015 40028.890.066 20.6690.082 915.3-17.407030.11568.81 4701 91017 60037.720.051 30.7440.091 123.54.107200.28181.41 2202 20019 100410.900.064 20.7230.071 918.37.737170.72881.91 4101 84012 80054.830.047 80.8130.062 815.6-16.907150.68270.51 7502 26016 900

4 讨 论

3.3节中Gamultiobj算法通过167次迭代获得了优化变量的最优解，由于种群的大小为200，相当于进行了33 400次弹道模型的计算。若采用搜索算法对目标函数组(12)的12个优化变量进行优化，即使每个变量取10个数值，模型的运算次数也高达1012次，远大于Gamultiobj的计算次数，可见Gamultiobj算法能够大幅度缩减目标函数组优化所需的时间。

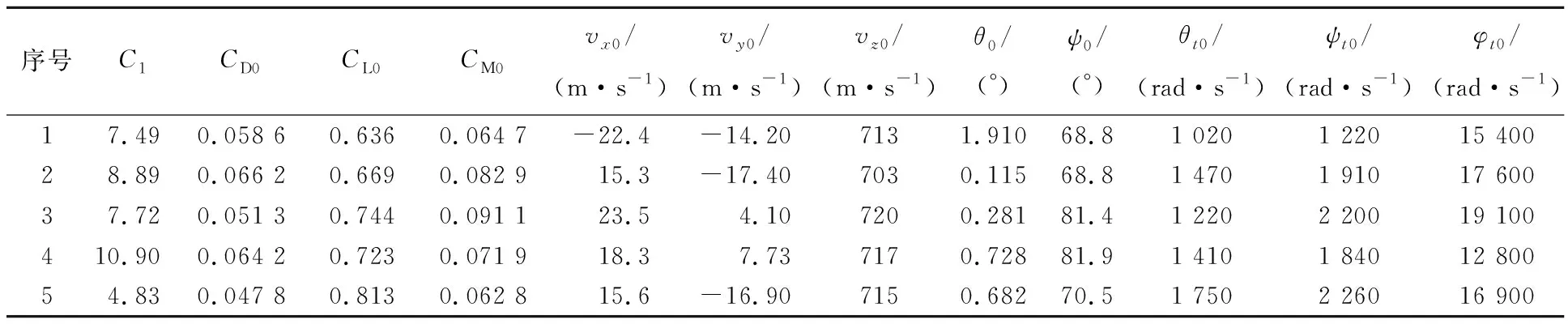
由Gamultiobj算法的基本原理可知，Pareto解集中的解与初始种群的构成有关[16]。表2中第2～5组最优解为采用随机生成法生成初始种群时其他4次优化得到的；它们对应的目标函数值如表3所示。可见虽然每次优化得到的最优解各不相同，但各最优解对应的均方根误差均较小，表明它们均能较好地模拟弹头的运动规律。由计算可知，最优解中力学系数C1、CD0、CL0、CM0的变异系数分别为0.278、0.138、0.095 8和0.162，弹头初始参数vx0、vy0、vz0、θ0、ψ0、θt0、ψt0和φt0对应的变异系数分别为1.83、1.67、0.009、0.945、0.091 1、0.200、0.224和0.146。除了由于vx0、vy0、θ0的均值接近零，导致其变异系数较大外，其他优化变量的变异系数均较小，表明所得最优解具有较强可信性。

表3 最优解对应的目标函数值Table 3 Values of objective functions corresponding to optimal solutions

5 结 论

在弹头侵彻明胶弹道模型的基础上，以弹头空间位置和姿态理论均方根误差作为目标函数，对7.62 mm步枪弹侵彻明胶的运动进行了模拟分析，得到以下结论：

(1) Gamultiobj算法和TOPSIS分析方法获得的弹头初始运动参数和弹道模型力学系数，能较好地模拟步枪弹侵彻明胶的空间运动过程，有助于揭示弹头对人体组织的致伤机理。

(2) Gamultiobj算法和TOPSIS分析方法能够快速获得优化变量的多组最优解。

(3) 优化变量的最优解与初始种群的构成有关，但所得的最优解变异系数较小，结果具有较强的可信性。