基于线结构光传感器的轨道板几何形貌检测方法
2018-10-15邵双运宋志军
祝 祥,邵双运,宋志军
(北京交通大学 理学院 光电检测所,北京 100044)
1 引 言
1.1 轨道板检测技术研究现状
随着科学技术的发展,我国的高铁时速已经突破300 km,高速行驶对轨道安全性提出了更高的要求。我国高铁与其他大多数国家一样,采用板式无砟轨道(CRTS型轨道板)铺设,并经历了CRTS I、CRTS ll、CRTS lll 三个发展阶段[1-3]。2009年开通的成都至都江堰客运路线,率先应用了板式无砟轨道成套技术,这是 CRTS lll型轨道板实际应用的第一次尝试。随后CRTS lll型轨道板被广泛应用于湖北,沈阳等地的客运铁路[4-6]。CRTS lll型板式无砟轨道由底板,承轨面,档肩等几部分组成。
与CRTS I型轨道板模板相比,CRTS lll型轨道板模板精度要求和加工难度更高[7-8],具体表现为:由于CRTS lll轨道板模底板模具上开有16个浇筑孔,导致底板整体易发生变形;承轨台部分的几何形状多样、对几何参数的精度要求比较高,铸造件表面平整度和坡度控制要求更高。轨道板的几何尺寸精度对于保证高速铁路的安全平稳运行起着重要作用,因此轨道板几个关键几何参数的测量具有重要的意义。
1.2 轨道板检测技术研究现状
国内轨道板检测技术起步较晚,初期多借鉴学习发达国家的检测技术,后来随着科学技术的进步,逐渐发展出了比较规范的检测技术。国内现有的轨道板检测方法主要有3种:游标卡尺法、全站仪法和激光三维成像法[9-10]。
游标卡尺法是最早应用于铁路现场的测量方法,一般由铁路工人使用游标卡尺直接对轨道板测量。利用游标卡尺和配套的工具,基本可以满足预埋套管、扣件间距等检测项目的测量需求。但对于轨道板整体的大范围几何尺寸,则需要使用钢尺进行测量,承轨面坡度需要使用坡度尺进行测量。游标卡尺法的缺点是需要耗费大量人力,并且属于接触式测量,在测量过程中存在安全隐患。
全站仪法检测属于单光点测量,是成都普罗米新科公司的专利技术“轨道板检测标架及其检测方法”[11]。其利用安装在轨道板承轨台上测量标架对轨道板进行定位,再将专用测量棱镜准确架设于测量标架上,结合全站仪的测角距参数具有较高精度,可以实现对轨道板各几何参数的测量;中铁12局集团有限公司提出了专利技术“一种用于CRTSⅡ型轨道板制板的检测方法”[12]。利用托盘模具精调工装,将平台式轨道板检测工装放在轨道板每个承轨台的挡肩面与承轨台台面上,结合精密角凹形球棱镜,通过无线控制全站仪双面观测每个承轨台特征点位的三维坐标,完成检测。和传统测量方法类似,现有的全站仪法需要的辅助工具过多,检测流程复杂,操作技术要求高,难以普及;并且检验速度慢,平均每块轨道板的检测时间超过50 min。在实际生产中,工厂的轨道板日产量约为100块,全站仪法不能完全满足实时测量要求,对于工厂来说,生产效率会受到影响[13]。
激光三维成像法主要利用激光三角位移原理进行测量。中国铁道科学研究院于2016年提出一种基于三维成像的轨道板快速测量方法[14],将三维数据和二维图像相结合,从而实现轨道板的快速检测。该方法测量速度快,检测结构比较简单,但在实际应用中,待测轨道板吊装时无法保证轨道板的基准边和基准面与机械扫描装置完全平行,对测量精度会产生较大影响。
1.3 本文的研究内容
综上所述,我国目前现有的轨道板检测方法都存在一定的固有缺陷,无法满足轨道板生产需求,影响企业的经济效益,也为高铁运行带来安全隐患。因此急需一种检测时间短,检测精度高,检测设备简单的轨道板测量方法。本文提出一种基于线结构光传感器的快速测量方法,利用单一轮廓即可获得轨道板的关键几何参数。搭建了完整的测量装置,完成了轨道板三维坐标数据的采集。受传感器位姿,噪声等影响,原始的三维点云数据与待测物真实三维形貌存在偏差[15-16],针对这一问题,本文提出一种基于三维点云数据的位姿校正方法,利用轨道板中特殊位置点云数据对整个点云数据进行位置和姿态的校正;根据特征参数定义,利用图像处理的相关算法对三维数据进行位姿校正,最终基于单条激光轮廓获得轨道板关键几何参数。
2 基于线结构光传感器的轨道板测量
2.1 线结构光测量方法
线结构光测量方法是一种主动式光学测量技术,由结构光投射器向被测物体表面投射光条,并由CCD从另一个角度获取光条的变形图像,依据光条的变形情况,可以获得待测物体表面的高度信息 。
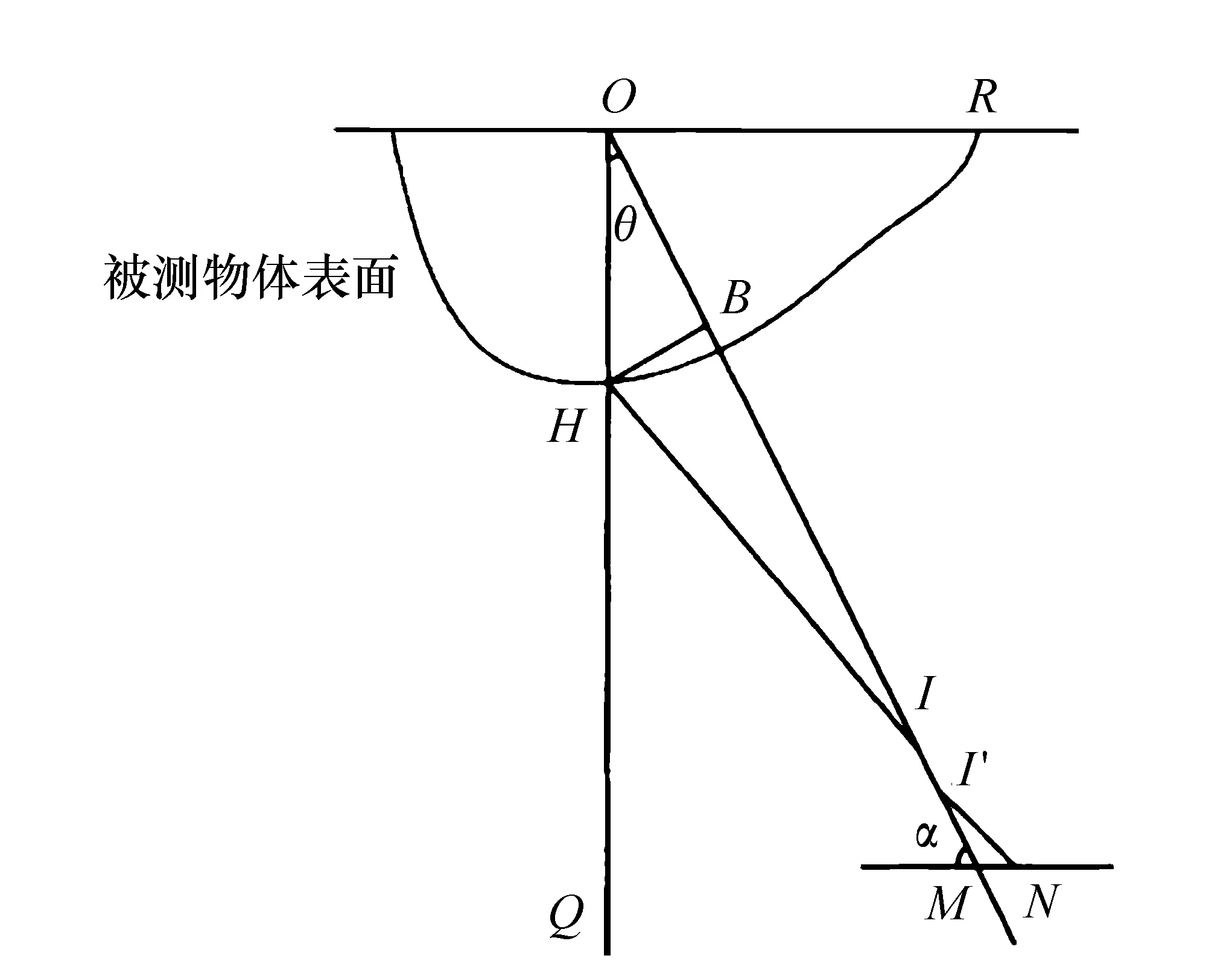
图1 三角法测量光路图 Fig.1 Optical path schematic of triangulation measurement
图1是线结构光三角法光路图,光源Q投射激光在待测物体表面H,OH为待测物体的高度信息,可以映射到像元表面距离MN,N点相对于中心像素M点的偏移量δ=MN。设相机的焦距为f,通过几何关系可得被测物表面高度信息OH与偏移量δ的关系如公式(1)所示:
(1)
在实际测量中,待测物体表面某一点的三维坐标信息(Xw,Yw,Zw),对应到相机成像平面上的某一像点(u,v),设μ为两坐标系的映射关系,则它们之间的关系可用公式(2)表示为:
(Xw,Yw,Zw)=μ(u,v) .
(2)
得到它们的对应关系之后,就可以恢复待测物体表面的高度信息,完成三维重构。
2.2 三维测量系统
本文所采用的测量装置如图2所示,包括线结构光传感器;编码器;电控位移平台;固定支架4个部分。激光器将线结构光投射到轨道板表面,与轨道板表面相切形成一条光刀,光刀会依据轨道板表面的形状产生变形,最后由相机采集变形的光条信息。

图2 测量装置图 Fig.2 Setup of measuring device
测量装置搭建完成之后,依照图3所示流程扫描轨道板,获取三维数据。

图3 测量过程流程图 Fig.3 Flow chart of measurement process
首先建立测量系统的世界坐标系。通过相机与激光平面之间相对位置的标定,确定坐标系的Xs-Zs轴,即激光平面为Xs-Zs平面。将传感器固定于电控位移平台上,电控位移平台沿Ys轴移动,与Xs-Zs平面垂直。电控位移平台的转轴与增量式编码器相连,步进电机每移动0.05 mm,编码器将会输出一个脉冲信号至传感器进行采样,传感器在Ys轴上两条轮廓之间的采样间隔为0.05 mm,同时通过串口通信,可以得到轨道板在电控位移平台移动方向Ys轴上的位置信息。至此,就获得了轨道板表面控位全部的XsYsZs三维点云数据。将编码器的脉冲信号和提取的光刀高度信息同步传入采集系统中,完成点云数据的采集过程。
测量时,选择轨道板的一侧作为采集起始位置,并在采集软件中设置采样间隔,考虑到轨道板的实际尺寸,每次的扫描长度设置为350 mm,采集完成后,软件自动生成三维坐标信息及灰度信息并传输到计算机,生成csv格式文件,如图4所示,测量完成。

图4 灰度信息和三维点云信息 Fig.4 Grayscale information and three dimensional point cloud information
3 点云数据的位姿校正
3.1 位姿误差的产生原因
如果在测量时,轨道板的位置和姿态比较理想,即轨道板底面与Xs-Zs平面垂直,与Xs-Ys平面平行,且传感器移动方向与承轨台长边垂直,可以基于单条激光轮廓提取轨道板参数。这种情况下处理的三维数据量小,算法简单,处理速度快。但该方法对于测量装置的位姿误差十分敏感。如图5所示,在实际测量过程中,三维点云数据的产生依赖于传感器和扫描装置构建的测量系统坐标系XsYsZs,而需要测量的轨道板几何参数是基于待测轨道板自身的世界坐标系XwYwZw定义的,在放置待测轨道板的过程中,无法保证两个坐标系完全重合,因此最终得到的三维点云数据会存在位姿误差。

图5 测量系统坐标系 Fig.5 Coordinate systems in measurement system
在实际的测量应用中,通过将传感器固定在步进电机上完成对轨道板的扫描。然而在扫描过程中,传感器的扫描方向Xs可能与轨道板径向Xw存在夹角如图6,导致在XsOsYs平面内的点云数据产生位姿偏移,无法直接用单条激光轮廓计算轨道板几何参数。
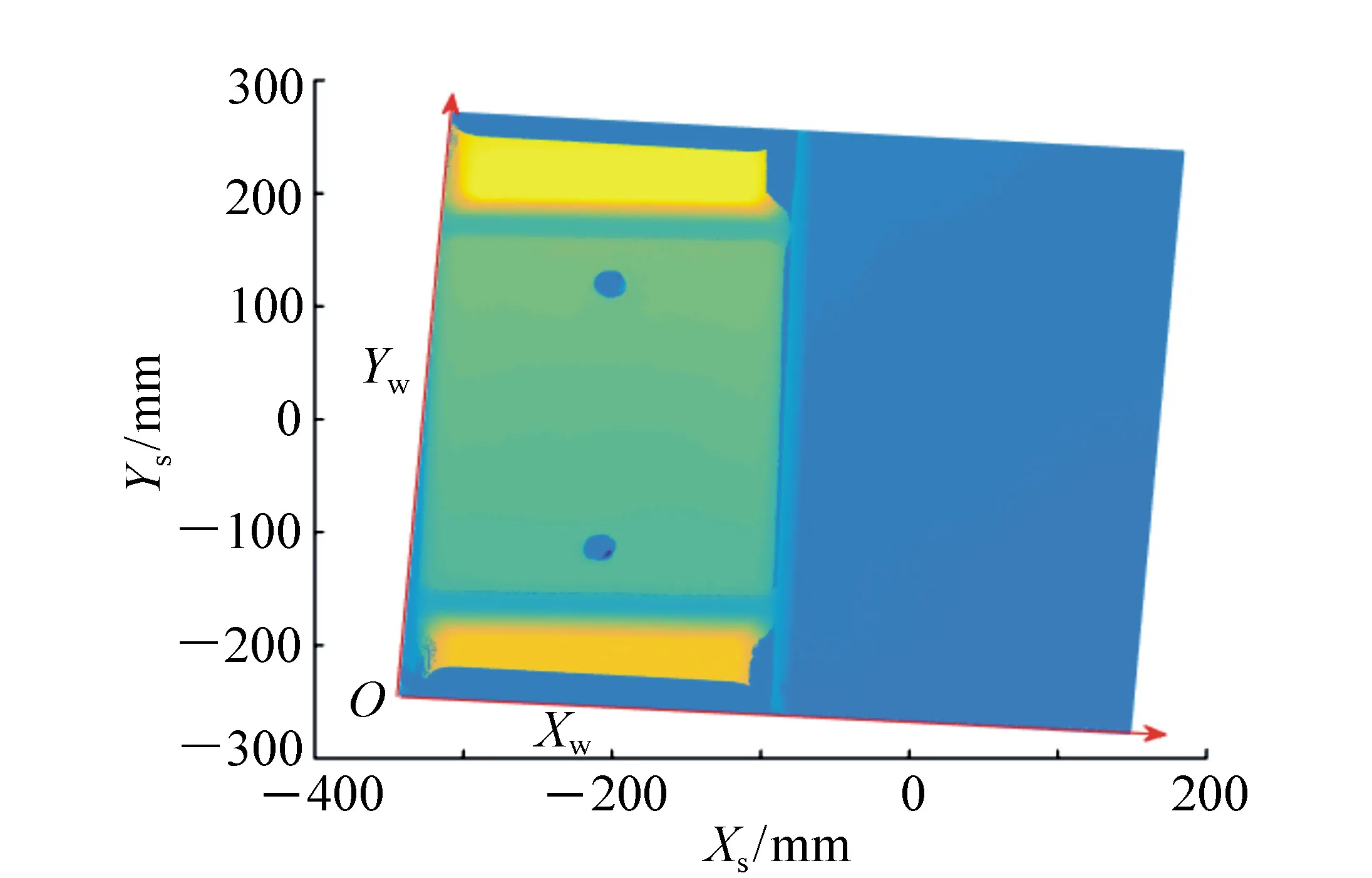
图6 扫描方向与轨道板中轴线存在夹角 Fig.6 Angle between the central axis of track plate and scanning direction
在放置轨道板的过程中,有可能因固定装置角度等问题导致轨道板不能水平放置,有一端会翘起,此时采集到的三维数据会发生变形,传感器的坐标系XsYsZs与轨道板的世界坐标系XwYwZw存在偏差,会对后续的数据处理产生影响。该位姿偏差可分解为3个坐标轴方向的夹角,两个坐标系X轴之间的夹角为θ1,Y轴之间夹角为θ2,Z轴之间夹角为θ3,如图7所示。

图7 两个坐标系之间存在偏差 Fig.7 Coordinate deviations between two coordinate systems
3.2 位姿校正方法

Δq={[(p+2p8+p7)·(p1+2p2+p3)]2+[(p3+2p6+p9)·(p1+2p4+p7)]2}1/2,
(3)
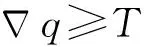

图8 位姿校正流程图 Fig.8 Flow chart of position and attitude correction

从图9(b)中可以看出,因为受到噪声的影响,轮廓边缘像素表现为离散、断裂的边缘特征。为了得到完整边缘线的直线方程,需要对该图像做霍夫变换。如图10所示,首先将边缘线段在笛卡尔坐标系下的坐标转换到极坐标系下,在笛卡尔坐标系下具有相同斜率和截距的直线上的点在极坐标系下具有相同的极坐标。因此同属于一条边缘直线的不连续边缘轮廓在极坐标系中会交于同一点。运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值,从而把检测直线的问题转化为统计峰值问题。

图9 (a)轨道板灰度矩阵图像;(b)边缘提取效果 Fig.9 (a)Grayscale matrix image of track plate; (b)extracted effect of edge

图10 霍夫变换中的坐标系转换 Fig.10 Coordinate transformation in Hough transform
在霍夫变换识别出一组候选峰值后,通过设置最短线段长度和目标角度区间,筛选出轨道板灰度图像中承轨面和底面之间的边缘线,得到直线方程y=kx+b,检测效果如图11所示。
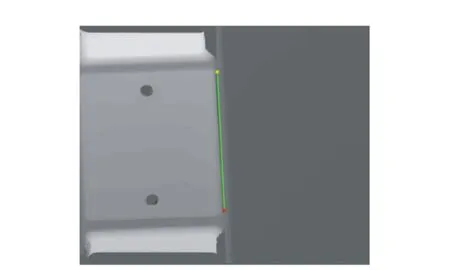
图11 霍夫变换检测到的边缘轮廓线 Fig.11 Edge contour detected by Hough transform
然后根据轨道板的几何形状特征进行区域分割,找到轨道板底板部分,使用最小二乘法对底板部分的点云数据进行平面拟合,设空间的平面方程为:
z=Ax+By+C,
(4)
式中,A、B、C为所要求取的拟合平面参数,待拟合点云数据为(xi,yi,zi),i=1,2,…,n,应使
(5)
最小,可得线性方程组
(6)
解上述线性方程组可得拟合平面方程参数A、B、C。拟合效果如图12所示。
通过霍夫变换找到的边缘直线方程和平面拟合得到的底面平面方程可以求解得到图7中θ1、θ2和θ3的值。则轨道板点云数据在这两个坐标

图12 平面拟合效果图 Fig.12 Effect diagram of fitting plane
系中的描述关系可用公式(7)表示为:
(7)
图13为位姿校正效果图。如图13所示,经过坐标系转换之后,三维测量过程中产生的位姿误差已被基本校正。
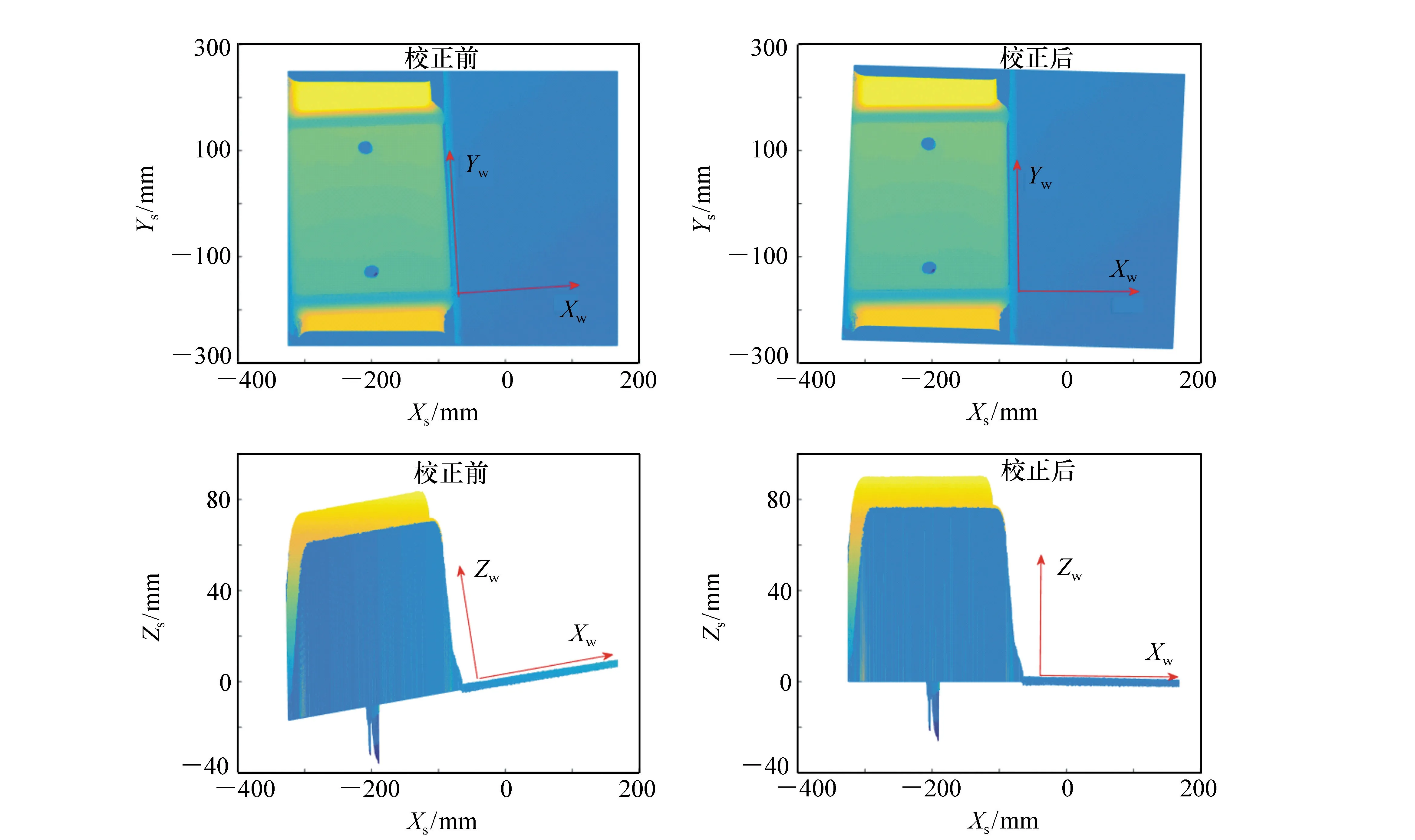
图13 位姿校正效果图 Fig.13 Position and attitude correction effect
4 实验结果与分析
中国铁路总公司在《中国铁路总公司高速铁路CRTS Ⅲ型板式无砟轨道先张法预应力混凝土轨道板暂行技术条件》中给出了“轨道板外形尺寸偏差及检测要求”,具体规定如表1所示。

表1 轨道板外形尺寸偏差及检测要求Tab.1 Dimension deviation and test requirements of track plate
利用本文提出的测量系统和数据处理方法,对轨道板生产厂家制作的CRTS Ⅲ型轨道板标准模具进行了测量。该轨道板几何尺寸经厂家检测,满足质量要求,可作为标准参照物。采用线结构光传感器对轨道板扫描后,得到如图4所示的点云信息。在此数据的基础上利用轨道板的几何参数定义,分别计算承轨面坡度,钳口夹角,钳口高度,小钳口距离等4项关键几何参数。首先对点云数据进行分区处理,找到承轨面部分,钳口内侧面部分和底面部分,用最小二乘法对这三部分分别进行平面拟合,得到3个平面方程,再根据两平面夹角公式即可计算出承轨面坡度。
在钳口两肩部分区域分别进行极值搜索,为避免偶然性,选取Z值最大的10个点取平均值,即可得到两侧的钳口高度。
根据轨道板的生产要求,小钳口距离定义为:轨道板承轨面平面垂直向上28 mm高度处,两个钳口内侧面之间的距离即为小钳口距离。基于此定义,将前面拟合得到的承轨面平面沿其法向方向向上平移28 mm,分别与两侧的钳口内侧面交于两点,两点间的距离即为小钳口距离,如图14所示。经过三维位姿校正之后的三维数据,可以利用单个轮廓直接求解各项几何参数,大大提升了计算速度和准确性。
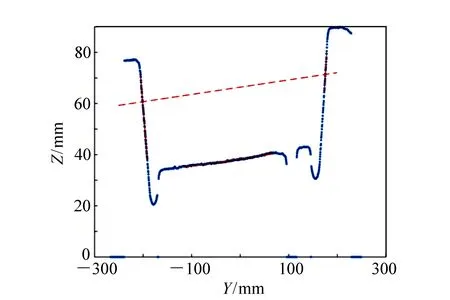
图14 轨道板轮廓图 Fig.14 Contour map of track plate
为验证传感器的检测效果,本文对标准轨道板模具进行了多次测量,得到轨道板的几项关键几何参数如表2所示。

表2 测量结果Tab.2 Measurement results
由表1和表2可知,在对三维点云数据进行位姿校正后,各项几何参数的测量精度均有较大提升,各项检测指标均符合技术要求。
5 结 论
本文提出了一种新的轨道板检测方法,其利用线结构光传感器快速,准确,非接触对轨道板进行三维测量和位姿校正。测量装置结构简单,测量速度快,承轨面坡度测量精度可达0.002°,钳口高度和钳口距离测量精度可达0.20 mm,满足《中国铁路总公司高速铁路CRTS Ⅲ型板式无砟轨道先张法预应力混凝土轨道板暂行技术条件》的检测要求。
