无人机侦察多目标实时定位技术研究
2018-10-15蔡明兵刘晶红
蔡明兵,刘晶红,徐 芳
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049)
1 引 言
无人机侦察具有实时性强、分辨率高、成本低、使用方便、无人员伤亡等优点,受到各军事大国的广泛重视。传统的无人侦察机是利用无人飞行平台搭载各种侦察设备,机载光电成像平台来实现对地面目标侦察定位,一般机载光电平台采用单点定位法,通过姿态测量/激光测距对目标定位。由于现代战场态势实时多变、目标数量众多,对多个目标进行实时定位需要多架无人机同时飞行侦察定位,或者频繁改变无人机飞行方向及改变光电平台空间方向(方位角、高低角),消耗大量时间同时增加了目标定位过程的误差。传统的单目标定位方法已经无法适应现代战场的需要,现代化战争中,谁优先掌握战场局面信息,谁就会取得胜利先机。因此研究一种新型高效的多目标实时定位技术是当前亟待解决的问题。
樊邦奎、段连飞等人[15]提出无人机空间两点交会的目标定位方法,以及Gregory J.Toussaint、Pedro De Lima等人[12]提出的基于多架无人机组合目标定位的方法,采用空间两点交会是提高定位精度的有效途径,在原有方法单点测量基础上增加第二个测量点,构成空间三角形,进行三角几何定位,这样需要对多架无人机,多个数据进行计算处理,既降低计算效率又增加成本。周前飞等人[14]给出一种基于像元视线向量的多目标自主定位系统来同时对多个目标实施定位。
针对上述多目标定位实时性较差、定位误差较大、耗资成本高等问题,本文提出了一种多目标实时自主定位的方法,该方法主要特点在于利用北斗卫星导航系统取代GPS卫星导航系统,采用三频北斗导航信号载波相位测量技术取代传统双频观测方法,实现北斗定位精度,以减小无人机空中定位误差;另一方面采用递归最小二乘法(RLS)对多帧图像的定位数据进行滤波处理,减小随机误差,提高定位精度。
2 多目标实时自主定位系统及工作原理
空对地的多目标定位目的是求取地面目标三维坐标值。如图1所示为本文将要采用的系统结构,它包括如图中的主要部分:机载光电测量平台,搭载北斗卫星导航定位系统及无人机空中姿态测量系统等。
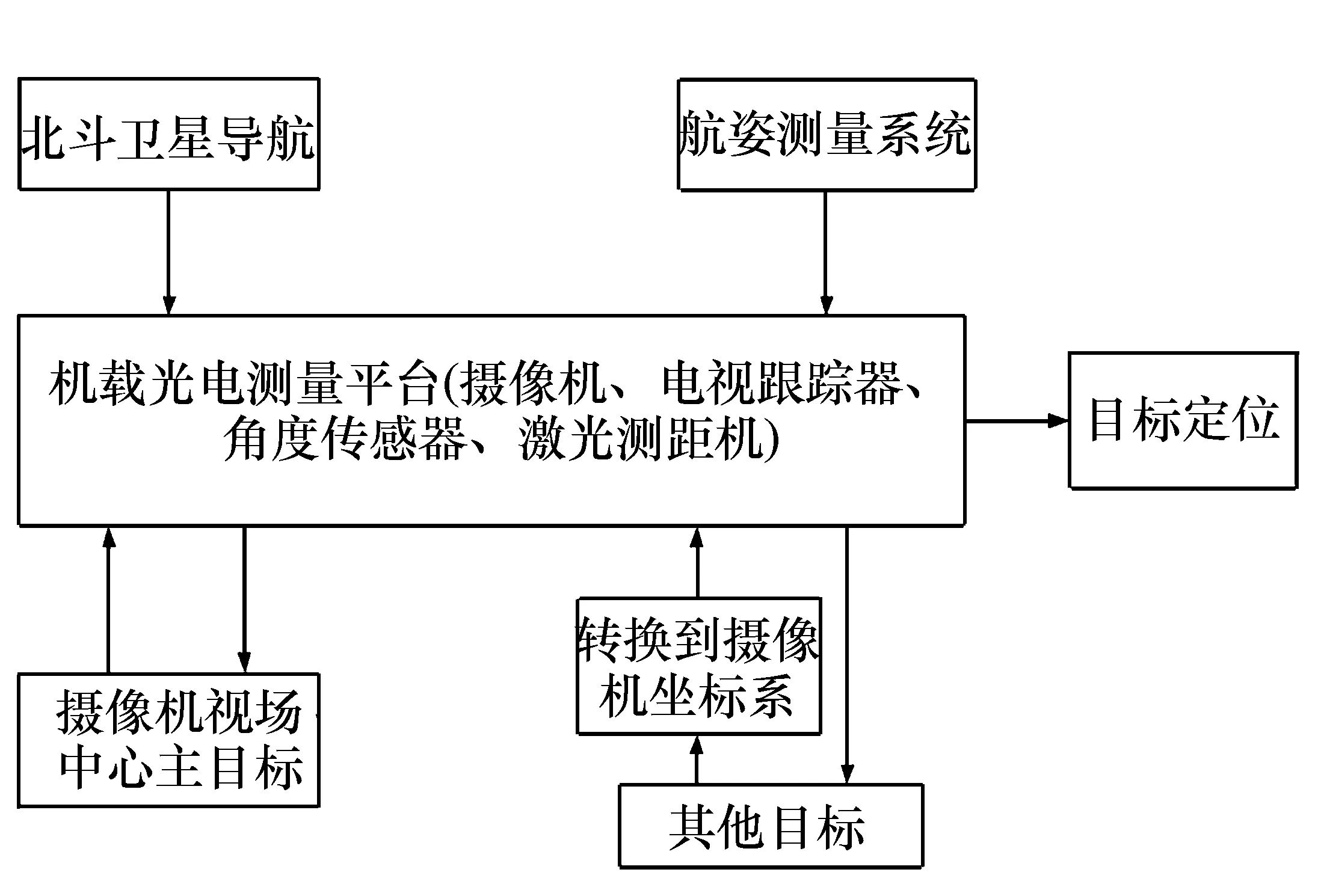
图1 多目标自主定位系统组成示意图 Fig.1 Sketch of multi-target self-determination system
北斗卫星导航定位系统和航空姿态测量系统与机载光电平台组为一体,消除平台对飞机的依赖性,减小误差,实现目标自主定位。
无人机对地面目标进行侦察定位过程中,搭载在机载光电平台上的摄像机搜索到地面目标,并将目标锁定到相机视场中心,根据北斗导航系统和航空姿态测量系统测得数据,无人机的空中三维坐标、三姿态角以及光电平台视轴的俯仰角和方位角、激光测距数据等信息,进行数据处理、坐标转换计算出目标的大地坐标。求解视场中的其余目标的大地坐标值,根据激光测距值、数码相机焦距及建立主次目标几何关系模型,计算次目标的大地坐标值。
3 目标定位算法与误差分析
3.1 机载目标定位基本原理
首先根据航拍图像中像点在相片坐标系中的位置,计算出像点在摄像机坐标系中的坐标,这里目标位于摄像机视场中心,在摄像机坐标系中的齐次坐标为[xcyczc1]T=[0 0λ11]T,然后经过从摄像机坐标系到载机机体坐标系的转换,再根据载机机体坐标系与载机地理坐标系间的转换关系到载机地理坐标系,然后经过地心地固坐标系最后到大地坐标系(这里是CGCS-2000坐标系)等多个坐标系的坐标转换,可计算出主目标在大地坐标系中的地理坐标。目标定位就是解决坐标系之间关系转换。
3.2 坐标转换数学模型
该系统使用了5个坐标系[14],如图2、图3所示。 摄像机坐标系Oc-xcyczc,载机机体坐标系Ob-xbybzb,载机地理坐标系Ov-xvyvzv,地固坐标Oe-xeyeze,大地坐标系O-LMH。其中摄像机坐标系的原点在摄像中心,其横轴(xc)和纵轴(yc)分别平行于像片平面的横行轴(u)和纵列轴(v)。
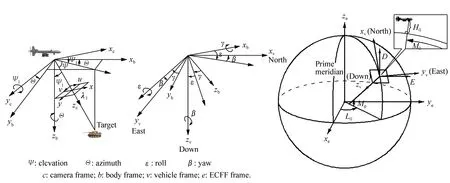
图2 各坐标系的定义及其相互关系示意图 Fig.2 Schematic diagram of definition of the coordinate system and their mutual relations

图3 目标自主定位的坐标转换流程 Fig.3 Process of self-determination orientation coordinate conversion
根据我们建立的坐标几何转换关系,依据坐标转换矩阵,依次计算主目标像点在各个坐标系中的坐标值,最后计算出主目标像点在地心地固直角坐标系(ECEF)中的坐标,公式(1)是从摄像机坐标转换矩阵依次到地心地固坐标的组合计算式:
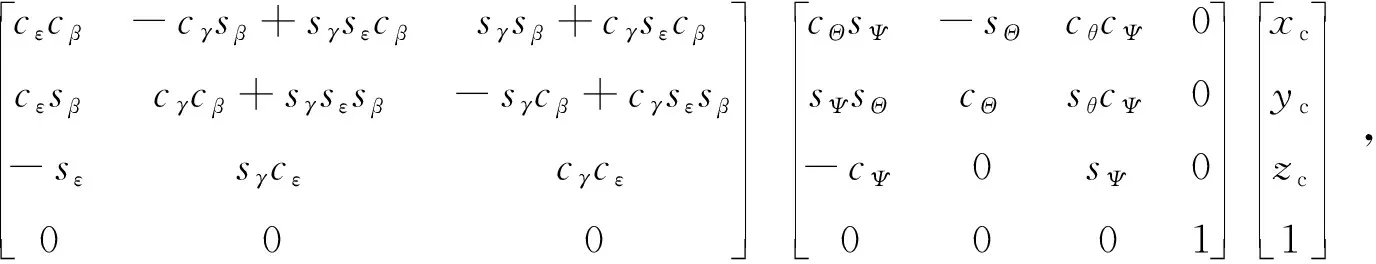
(1)
其中,cΩ=cos(Ω),sΩ=sin(Ω)。
然后根据上述转换计算公式(2)~(5)求解目标像点从地心空间直角坐标系(ECEF)到大地坐标系(geodetic)的大地坐标如下:
(2)
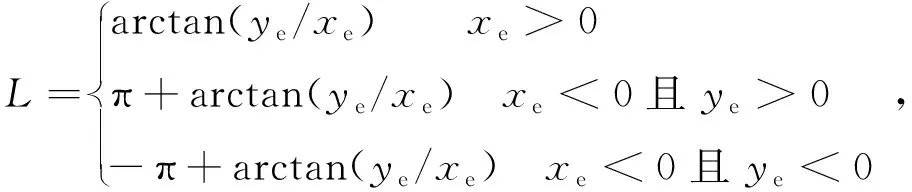
(3)
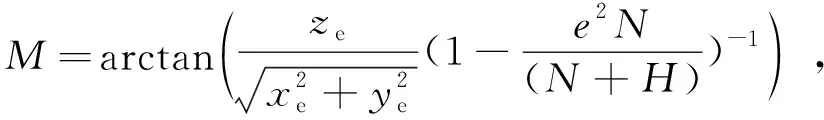
(4)
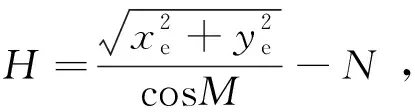
(5)
式(2)~(5)中:L、M、H分别为目标在大地坐标系中的大地经度,大地纬度和大地高程。其中,在CGCS-2000大地坐标系中,
椭球长半轴a=6 378 137.0 m;
椭球短半轴b=6 356 752.0 m;
根据以上的坐标转换计算过程,就可以计算得到主目标在大地坐标系中的坐标。要求解像平面内的次余目标大地坐标,要根据建立的几何关系模型,通过测量计算主次目标之间的几何角度关系计算得到次目标像点在摄像机坐标系下的三维坐标(xcyczc),然后根据计算主目标的过程(1)~(5)式的坐标转换方法计算次目标大地坐标。设定各目标处于地势平坦的大地上,光电平台与各目标之间的相对高度均为h,建立几何定位模型如图4所示。
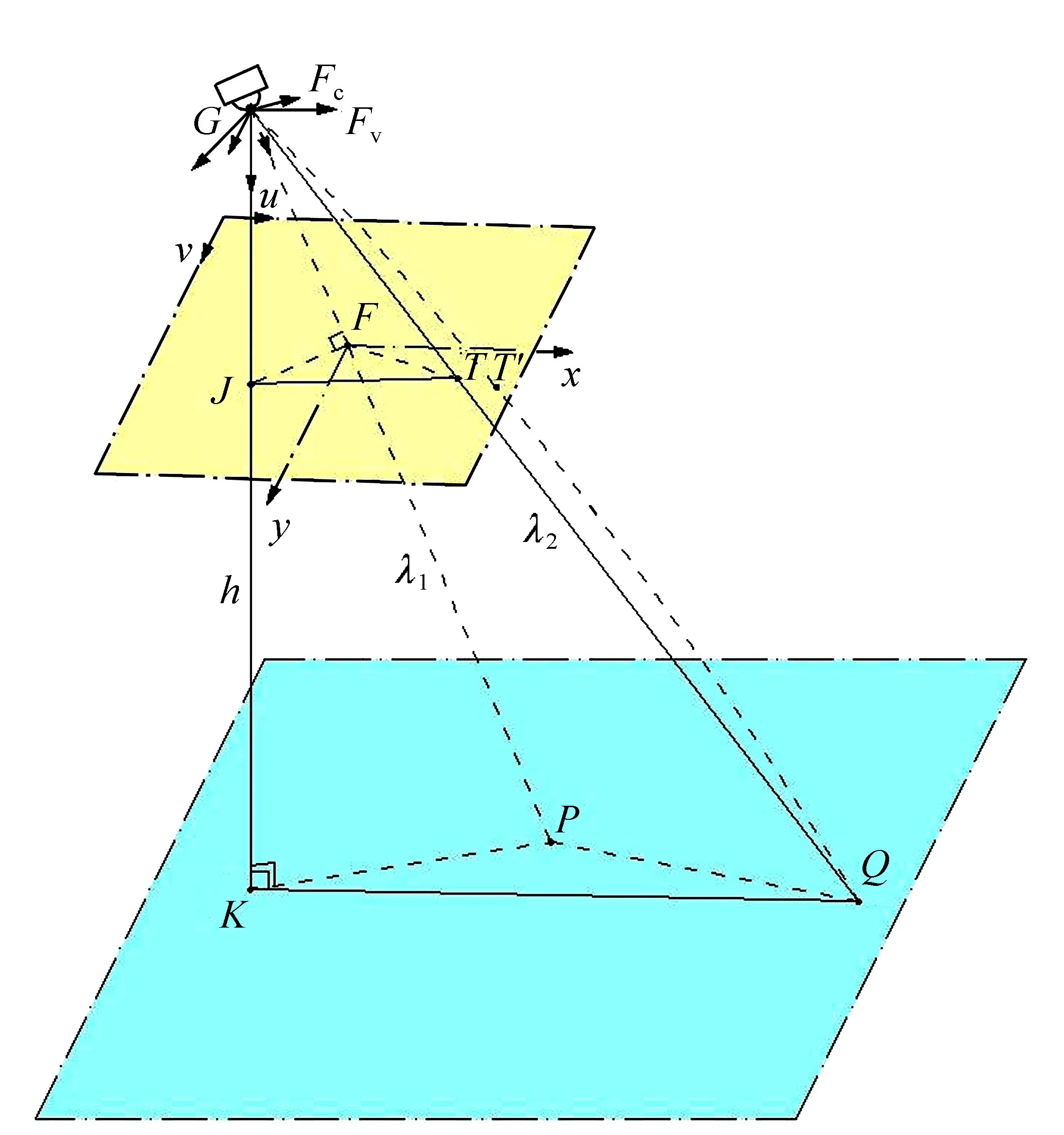
图4 多目标定位模型 Fig.4 Model of multi-target orientation

h=λ1cosα,
(6)

(7)

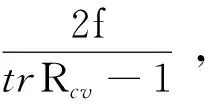
(8)
视线向量j沿载机地理坐标系的zv轴向下,
(9)
Rcb为从载机机体坐标系到摄像机坐标系的转换矩阵,其余以此类推。
求解j在摄像机坐标系下的坐标为:
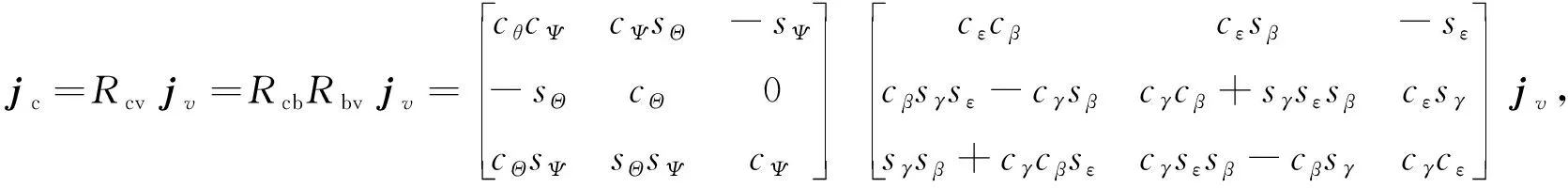
(10)
将式(8)求得的jvz的值代入式(9)、(10)中,求得在摄像机坐标系下的坐标jc,下步将jc代入上式(7)中得到数据值cosα、cosβ,前面激光测距仪测得的主目标离光电平台的距离λ1,根据公式(6)计算平台目标间的相对高度h和次目标到光电平台的距离λ2。根据求得的次目标离平台距离及其在摄像机坐标系下的视线向量j,可根据式(11)求得次目标在摄像机坐标系下坐标,

图5 坐标转换流程 Fig.5 Process of coordinate conversion
(11)
综上所述,计算次目标大地坐标是根据主次目标几何关系求出其在摄像机坐标系下坐标,然后将该坐标值代入(1)~(5)式计算次目标的大地坐标,在计算多目标坐标转换流程如图5所示。
4 北斗导航厘米级定位精度实现
目标的定位精度是无人机侦察定位系统的最重要指标,在无人机定位系统设计中占有重要地位。目标定位误差主要有以下几种误差组成:无人机空中定位误差、无人机姿态角误差、激光测距误差及光轴稳定平台误差等。
针对无人机空中定位误差,卫星导航系统扮演了重要角色,美国全球导航系统(GPS)在以往定位中起到重要作用,由于战时形势严峻,如果单纯依靠GPS定位,将会处处受制于人。
中国研制的北斗卫星导航系统区别于GPS的特征在于,北斗卫星较GPS多3颗中轨道卫星(MEO),即27颗中轨道卫星(分布在倾角55度的3个平面上),此外还有5颗静止轨道卫星(GEO)和3颗倾斜同步卫星(IGSO),北斗还具有GPS不具备的短报文通信能力。
通过解读北斗卫星导航系统空间信号接口控制文件公开服务信号[BDS-SIS-ICD-2.0(2013.12)],采用三频北斗导航信号能够实现北斗厘米级定位,三频北斗导航信号B1、B2、B3。其中B3为加密信号,使用需得到相关授权,B1、B2信号表达式分别如式(11)所示:
其中,上角标j表示卫星编号;下角标I表示I支路;下角标Q表示Q支路;A表示信号振幅;C表示测距码;D表示调制在测距码的数据码;f表示载波频率;φ表示信号载波初相。

(12)
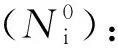
其中:
解得:
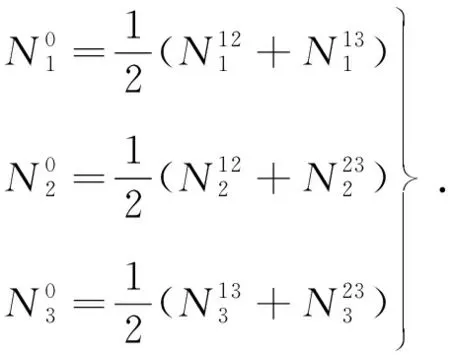
(13)
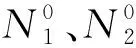
5实验仿真与分析
实验分为以下3部分:
(1)对“北斗二代”进行星座仿真(由于采用的是MEO星座,所以这里仅对27颗MEO星星座仿真)。
(2)采用蒙特卡洛法对多目标定位误差进行仿真分析。
(3)采用最小二乘算法(RLS)对图像进行滤波处理,减小随机误差,提高目标地位精度。
实验一:北斗二代星座仿真
根据美国Trimble公司的 Center-Point RTX 全球跟踪网于2013年春天对北斗GEO-3、IGEO-6和MEO-14卫星三频导航信号的测量成果可知,3颗北斗卫星的载波相位观测值均能达到±11 mm左右的测量精度,因此在无人机目标侦察定位系统采用三频北斗导航信号能够使目标定位精度有很大提高。
根据公示的北斗卫星导航系统空间信号接口控制文件公开服务信号[BDS-SIS-ICD-2.0(2013.12)],对北斗二代星座仿真,然后基于此仿真测量无人机空中定位精度。
如图6是对27颗MEO卫星星座仿真。
图6 北斗MEO卫星仿真图 Fig.6 Simulation figure of BDS-MEO
设飞机地面之间相对高度为1 200 m,飞行位置经度为122.672 813°,纬度为45.125 187°。
如图7是在仿真星座模型下对无人机空中定位精度结果,北斗定位系统固有精度对应经度误差为1×10-4(°),纬度误差为 2×10-4(°),对应东向误差为10 m,北向误差为20 m左右,大地高误差小于10 m,授时精度为20 ns,测速精度为0.2 m/s。
以某航拍图像数据作为实验对象。光电平台
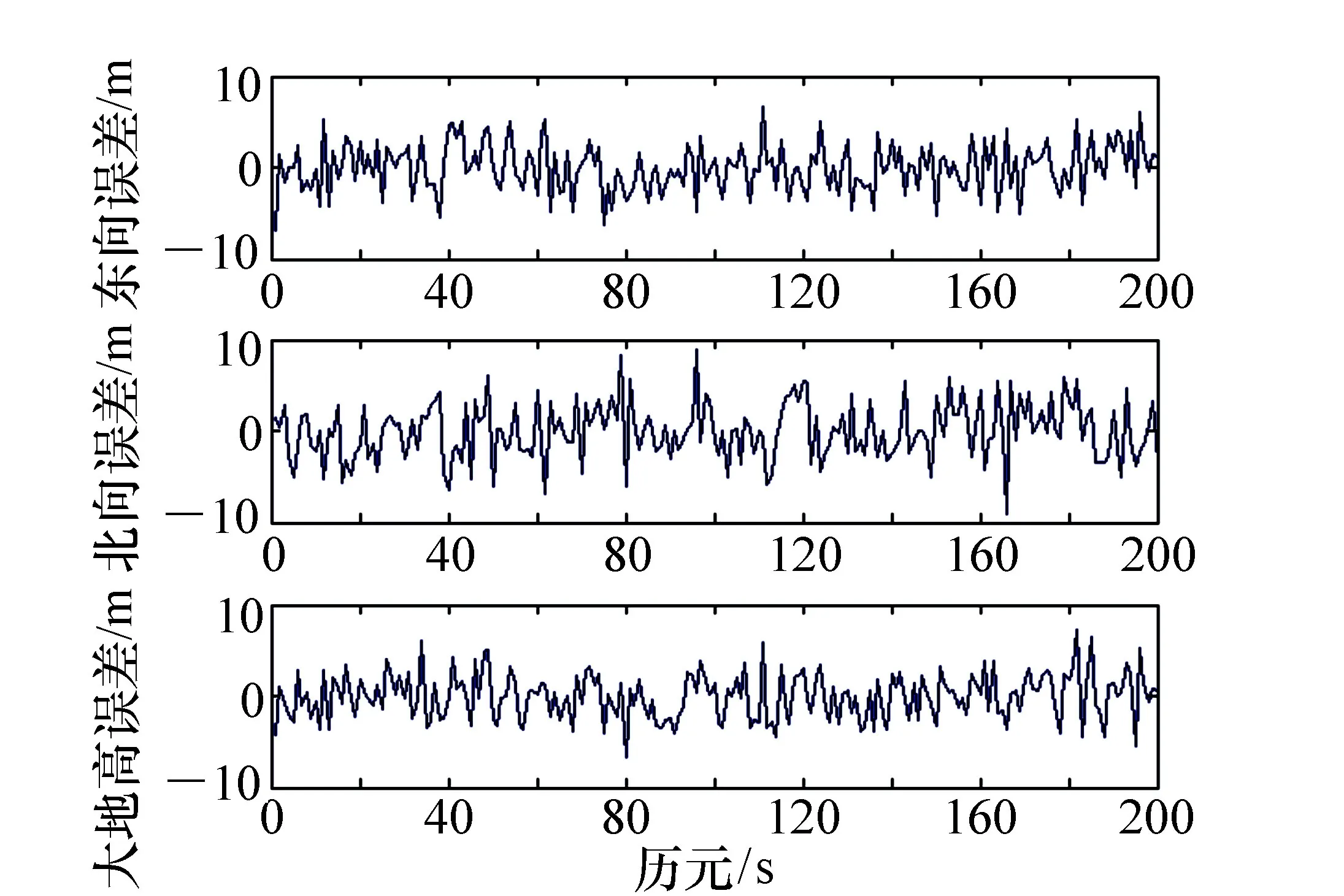
图7 北斗仿真定位误差 Fig.7 Localization errors of BDS
俯仰轴以水平方向为0°,垂直向下为-90°。平台高低角为-90°(垂直下视)时,平台方位角为0°, 高低角和方位角的测量误差为0.5 mrad(约0.028 65°),激光测距精度为5 m。
实验二:蒙特卡洛法多目标定位误差分析
蒙特卡洛法是一种通过计算大量数据,随机模拟,计算数据概率的一种方法,是一种随机抽样技术。利用蒙特卡洛法根据随机数据解决很多实际计算问题。
蒙特卡洛法的理论基础为大数定理和伯努利定理,根据蒙特卡洛法建立目标定位误差模型:
[ΔLΔMΔH]T=F′(X)-F′(X-ΔX) ,
(14)
式中:ΔL、ΔM、ΔH为目标的定位误差,ΔX为定位参数误差,F为目标定位模型。视场内3个目标的定位误差如表1所示。

表1 多目标定位误差Tab.1 Error of multi-target location
实验三:实现地面多目标定位的RLS滤波
最小二乘算法是一种通过最小化误差的平方和找到一组数据的最佳匹配方法。最小二乘法是用最简单的方法求得一些误差值,使数据趋近真值。在这里采用递归最小二乘算法对数据进行滤波处理,减小随机误差,提高目标定位误差。
RLS滤波算法如表2所示。

表2 RLS算法流程Tab.2 Flowchart of RLS algorithm
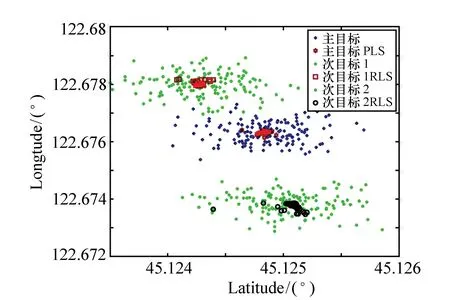
图8 RLS滤波后的定位结果 Fig.8 Localization results after RLS filtering

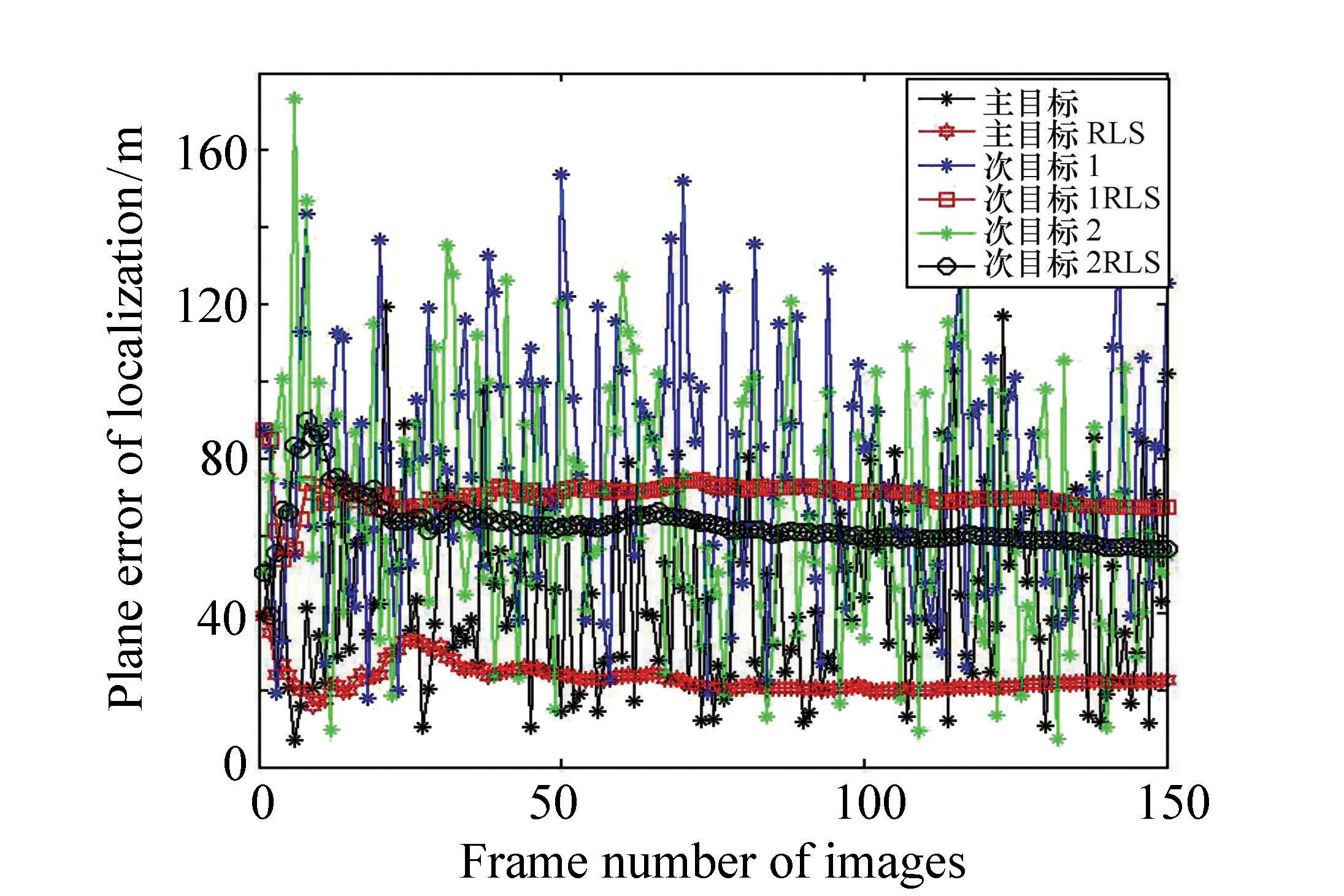
图9 RLS滤波后的定位误差 Fig.9 Plane localization errors after RLS filtering

图10 RLS滤波后的高程定位误差 Fig.10 Altitude localization errors after RLS filtering
经过RLS滤波处理后的各目标定位误差如表3所示。

表3 RLS滤波后多目标定位误差Tab.3 Errors of multi-target location after RLS filter
6 结 论
(1)提出了一种基于无人机侦察多目标实时定位技术,该方法只需激光测距机对地面主目标进行一次测距,然后根据摄像机焦距及摄取图像上各目标像素坐标即可求出其余各目标大地坐标,该技术用于地面平坦战场,较之传统单目标定位,该技术能大大提高无人机侦察效率。
(2)此外,也提出了利用北斗导航系统对无人机进行空中定位,“北斗二代”组网成功预示着利用北斗导航将会对定位精度有质的提高。
(3)同时,采用递归最小二乘算法进行滤波,有效减小定位过程随机误差,提高目标定位精度10 m左右。
(4)接下来要进一步解决的问题是在地形复杂情况下如何实现多目标快速实时定位。
