基于EOF法的长江流域1960—2015年降雨侵蚀力时空变化特征研究

庞延杰，董林垚，丁文峰，张平仓，朱秀迪

(1.长江水利委员会 长江科学院，湖北 武汉 430010；2.水利部 山洪地质灾害防治工程技术研究中心，湖北 武汉 430010)

降雨侵蚀力反映了降雨引起土壤侵蚀的潜在能力，是一种对引起土壤侵蚀的气候因子的定量评价指标[1]。降雨侵蚀力通常用R指标来表示，它首次出现在WISCHMEIER et al.[2]提出的建立在美国东部降雨-径流观测数据基础上的通用土壤侵蚀模型(USLE)中[3]。随后，R指标受到广大学者的推崇，并应用于各国土壤侵蚀模型的构建和水土保持规划工作中。R指标与降雨强度、降雨量、降雨历时等降雨参数有关[4]，国内外学者通常使用不同时间段的次降雨总动能(E)和雨强(I)组合来计算降雨侵蚀力。考虑到这种算法是建立在基于小时或分钟雨量信息观测数据基础上的，资料的获取有一定难度，章文波等[4-5]等根据日降雨量资料构建了更简易的算法。由于日降雨量资料相对容易获得，且能够提供丰富的降雨特征信息，可以近似估算降雨侵蚀力，因此被广泛应用于降雨侵蚀力时空变化特征分析[6-8]。

区域降雨侵蚀力时空变化特征的研究对于区域水土流失量预测预报、水土保持措施制定和农业发展战略研究具有重要的现实意义。当前国内关于区域尺度降雨侵蚀力时空变化特征的研究多侧重于区域均值或单个站点降雨侵蚀力的趋势、突变及周期分析，而对降雨侵蚀力时空变化的信息特征提取不足[9-13]。经验正交函数(EOF)分析法在大气、海洋等地球物理科学的数据分析领域应用广泛，能够将复杂的地学系统分解为若干个相互正交模态的正交组合，并提取其主要时空变化特征。EOF法被广泛地应用于长江流域气温、降雨和洪涝灾害时空变化特征及其对大气环流因子的响应研究[9-11]。考虑到基于EOF法对长江流域降雨侵蚀力时空变化特征的研究成果不多，本研究以长江流域内186个雨量站的日降雨资料为基础，应用日雨量的降雨侵蚀力模型计算长江流域1960—2015年多年平均降雨侵蚀力，使用EOF法提取降雨侵蚀力的时空变化特征，以期为长江流域水土流失研究和水土保持措施制定提供科学依据。

1 研究区域与研究数据

长江流域位于90°33′～122°25′E、24°30′～35°45′N(图1)，流域面积180万km2，涉及19个省、自治区和直辖市，流域人口约占全国总人口的1/3。长江流域上游为深切割高原区，中上游为切割山地区，中下游为低山丘陵与平原区。流域内年均气温为-4～20 ℃，并呈东高西低、南高北低的分布趋势。流域内地域辽阔、地形复杂，季风气候特征十分典型，降水量和暴雨的时空分布很不均匀，除江源地区年均降水量小于400 mm，四川盆地西部和东部边缘、江西和湖南、湖北部分地区年均降水量大于1 600 mm外，大部分地区年均降水量在800～1 600 mm之间。长江流域水丰沙富，据大通站资料，年径流总量为9 240亿m3，汛期(5—10月)径流量占年径流总量的71.7%，年均含沙量为0.544 kg/m3，年均输沙量为4.86亿t。

本研究采用1960—2015年长江流域186个雨量站的日降雨量，数据来源于中国气象数据网(http://data.cma.cn/site/index.html)，各雨量站数据完备，无缺测漏测。根据长江流域地理及水系分布特征，将流域划分为11个区域：区域一为金沙江水系，包含雨量站27个；区域二为沱江水系，包含雨量站11个；区域三为嘉陵江水系，包含雨量站11个；区域四为上游干流区间，包含雨量站25个；区域五为乌江水系，包含雨量站14个；区域六为汉江水系，包含雨量站11个；区域七为中游干流区间，包含雨量站39个；区域八为洞庭湖水系，包含雨量站24个；区域九为下游干流区间，包含雨量站16个；区域十为鄱阳湖水系，包含雨量站8个；区域十一为太湖水系，无雨量站。各雨量站分布详见图1。

2 研究方法

2.1 降雨侵蚀力计算方法

本研究采用基于日雨量资料的降雨侵蚀力计算模型，其计算公式[4-5]为

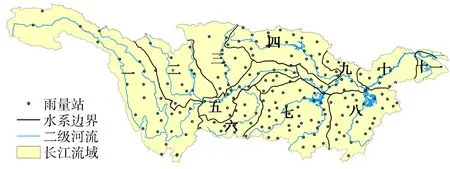
图1 长江流域区域划分及雨量站分布

(1)

(2)

α=21.586β7.189 1

(3)

(4)

上式中：R为年降雨侵蚀力，MJ·mm/(hm2·h)；Ri为第i个半月时段的降雨侵蚀力，MJ·mm/(hm2·h)；k为半月时段内的降雨天数；Pj为半月时段内第j天的侵蚀性降雨量，mm，取日降雨量≥12 mm作为侵蚀性降雨的判别标准；α、β为模型参数；Pd12为日雨量≥12 mm的日平均降雨量，mm；Py12为日雨量≥12 mm的年降雨量，mm。

2.2 EOF方法

经验正交函数(EOF)分析法也称主成分分析法(PCA)，是一种提取主要数据特征量的方法，其计算步骤[14-15]为：

(1)对要分析的数据进行预处理，通常处理为距平形式。标准化处理后得到一个数据矩阵Xm×n，其中m为站点数，n为年数。

(2)计算矩阵Xm×n与其转置矩阵Xn×m的交叉积，结果为相关系数矩阵Cm×m。

(3)计算Cm×m的特征根矩阵Em×m和特征向量Vm×m，其中Em×m是由特征根组成的对角矩阵，即

(5)

每个特征根λi对应特征向量Em×m的第i列，是对应的第i个EOF模态。

(4)将EOF投影到原始资料矩阵上，得到空间特征向量对应的时间系数(主成分)，即

(6)

式中：PCm×n的每行数据是对应特征向量的时间系数。

(5)第k个模态对总方差的贡献率为

(7)

(6)EOF结果的显著性检验一般通过与随机或者虚假数据EOF分析结果进行比较，在95%置信度水平下，特征根的误差[12]为

(8)

式中：N*为数据的有效自由度。

将特征根λi按顺序依次检查，标上误差范围。如果前后两个特征根λi之间的误差范围无重叠，则通过显著性检验。

3 结果与分析

3.1 降雨侵蚀力计算结果

利用公式(1)、(2)、(3)、(4)对长江流域186个雨量站1960—2015年历年降雨侵蚀力进行计算，求均值后得到各个站点的多年平均降雨侵蚀力，通过Kriging插值法计算得到长江流域年均降雨侵蚀力空间分布，见图2(a)。长江流域年均降雨侵蚀力值变化范围为114.423～16 233.136 MJ·mm/(hm2·h)，平均值为5 855.716 MJ·mm/(hm2·h)，标准差为3 057.963 MJ·mm/(hm2·h)。相比黄土高原地区[6]和珠江流域[8]，长江流域年均降雨侵蚀力均值虽介于两者之间，但其空间差异却更大。长江流域降雨侵蚀力总体上从西北向东南递增：降雨侵蚀力低值主要分布在金沙江水系、岷沱江水系北部、嘉陵江水系西北部和汉江水系东部；降雨侵蚀力高值主要分布在下游干流区间、鄱阳湖水系和洞庭湖水系。上述结果与HUANG et al.[7]对长江流域1965—2005年降雨侵蚀力分析结果大致相同。

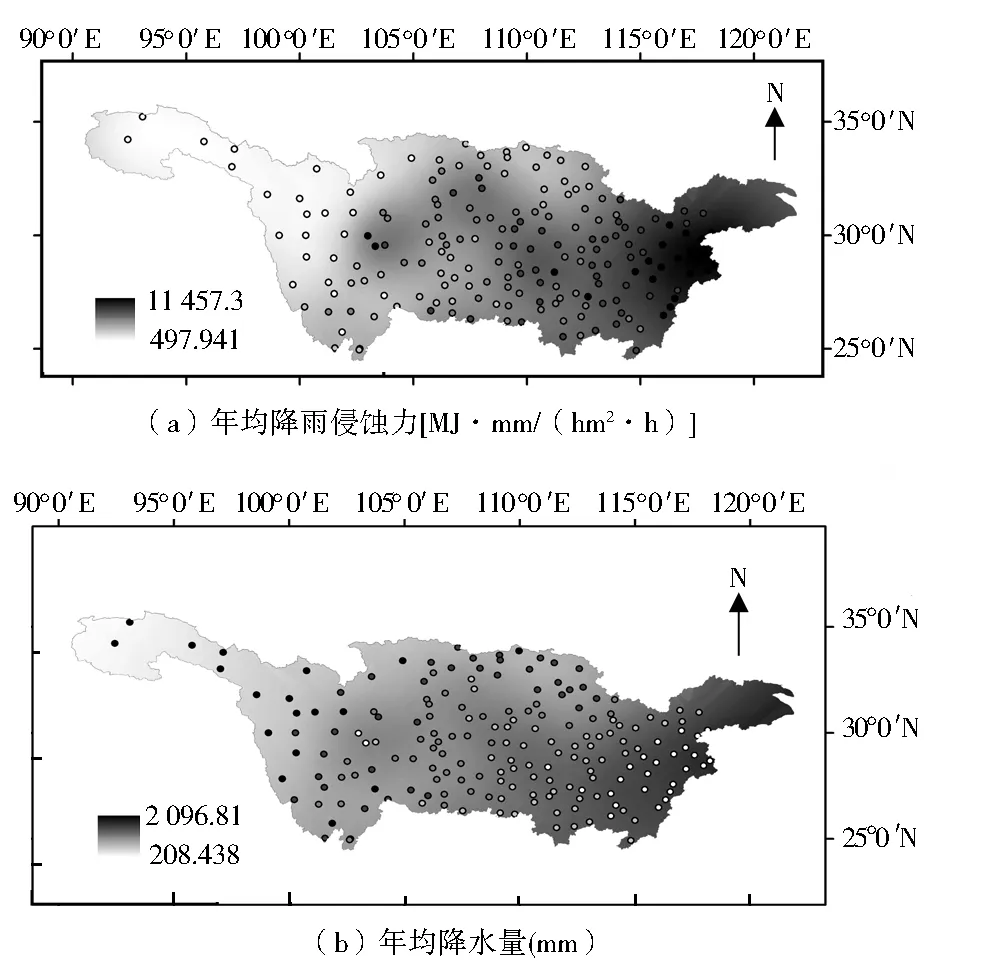
图2 1960—2015年长江流域多年平均降雨侵蚀力、降水量分布

由图2可知，长江流域多年平均降雨侵蚀力、降水量的空间分布规律基本一致，说明降水量的空间分布结果对于研究降雨侵蚀力具有很好的借鉴作用。采取线性回归方法构建长江流域年均降雨侵蚀力与经度、纬度、海拔和年均降水量之间的相关关系，结果表明(图3)：年均降雨侵蚀力总体上随着经度的增加而增加(R2=0.606，p<0.01)，随着纬度的增加而减小(R2=0.096，p<0.01)，随着海拔升高而减小(R2=0.403，p<0.01)，与年均降水量呈极显著的正相关关系(R2=0.901，p<0.01)。

图3 长江流域多年平均降雨侵蚀力与经度、纬度、海拔和年均降水量的相关关系

3.2 空间分布特征

应用EOF法对长江流域1960—2015年降雨侵蚀力进行时空分解，并进行显著性检验，得到降雨侵蚀力的主要空间分布模态。EOF分解的特征向量贡献率及显著性检验结果表明，前4个特征向量特征值的误差范围不重叠，通过North显著性检验，累积贡献率达46.39%，因此前4个特征向量可以较好地解释长江流域1960—2015年降雨侵蚀力的空间分布特征。

模态第一特征向量的方差贡献率为24.73%，高于其他模态的贡献率，是长江流域降雨侵蚀力的主要空间分布形式。图4(a)显示，除金沙江上游部分区域外，其他站点的特征值均为正值，表明1960—2015年长江流域大部分地区降雨侵蚀力变化趋势具有高度一致性，即同时呈现高值或低值的状况。第一模态的特征值呈现由西向东递增的趋势，反映长江下游地区降雨侵蚀力波动程度比上中游地区大。高值中心位于下游干流区间东部、鄱阳湖水系东北部和太湖水系，反映该区域降雨侵蚀力变化量较大。

图4 长江流域降雨侵蚀力EOF分析第一、第二、第三和第四模态特征值空间分布

模态第二特征向量的方差贡献率为10.75%，也是长江流域降雨侵蚀力的主要空间分布形式。图4(b)显示，除洞庭湖水系、鄱阳湖水系、四川盆地和长江上游局部地区外，长江流域其他地区均为正值区，因此洞庭湖水系、鄱阳湖水系、四川盆地和长江上游局部地区降雨侵蚀力会呈现与长江流域其他地区不同的震荡类型。正值高值中心位于长江中下游河段以北区域，负值高值中心处于鄱阳湖流域东南，表明上述区域降雨侵蚀力变化较大。

模态第三特征向量和第四特征向量的方差贡献率分别为6.18%和4.73%，反映了降雨侵蚀力空间分布的局部特征。模态第三特征向量和第四特征向量在金沙江流域、洞庭湖流域和鄱阳湖流域均呈正值，即具有相近的震荡类型，而在其他地区正负值不同，呈现互补的变化特征。

3.3 时间变化特征

根据降雨侵蚀力空间分布特征分析结果，长江流域降雨侵蚀力场主要有4种表现类型，其中第一模态和第二模态为降雨侵蚀力的主要空间变化特征。时间系数代表了所对应特征向量空间分布模态的时间变化特征，系数的符号表示与模态震荡类型的异同，绝对值的大小表示模态的典型程度。为了分析降雨侵蚀力场的时间变化特征，分别采用线性趋势分析和小波变换方法分析降雨侵蚀力的变化趋势和震荡周期。

降雨侵蚀力前四个模态时间变化系数及线性趋势见图5。第一模态时间趋势斜率大于零，其显著性检验p值小于0.1，在一定程度上说明长江流域降雨侵蚀力总体上随时间呈增加趋势，每年的增加量约为290 MJ·mm/(hm2·h)。第一模态时间系数极大值对应年份为1998年，与长江流域强降雨引发全面洪灾相对应；极小值对应年份为1978年，与长江流域中下游地区特大干旱事件对应。第二、三、四模态时间系数趋势分析的显著性检验p值均大于0.1，表明这三个模态的线性变换趋势不明显。该拟合结果说明利用时间变化系数可有效反映年降雨侵蚀力极值点出现的时间，同时对于预测未来几年降雨侵蚀力的变化趋势有一定的借鉴作用。

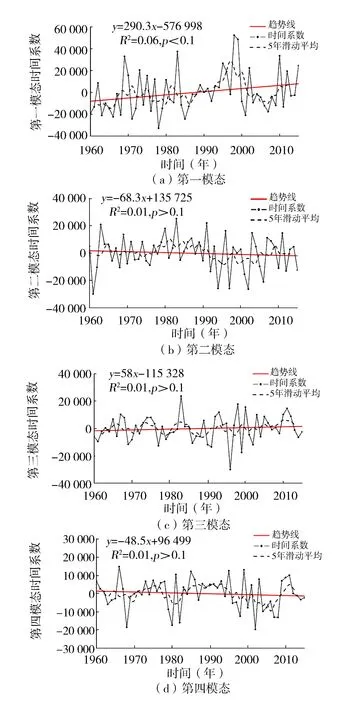
图5 长江流域降雨侵蚀力第一、第二、第三和第四模态时间系数

降雨侵蚀力前四个模态的时间系数均呈周期性波动，为了探究降雨侵蚀力变化的显著周期，使用小波变换工具对降雨侵蚀力前四个模态时间系数进行功率谱计算。第一模态时间系数波动周期集中在2～5 a；第二模态时间系数波动周期集中在2～5 a；第三模态时间系数波动周期集中在1～11 a，第四模态时间系数波动周期不显著。第一模态时间系数小波功率谱分析结果表明长江流域降雨侵蚀力总体上呈2～5 a周期波动，在1995—2005年间波动最为明显，与此期间全流域降雨在2～5 a周期变化相关；第二模态时间系数小波功率谱分析显示，1990—2010年间长江流域中下游河段以北与鄱阳湖流域东南在2～5 a的周期呈干湿交替变化，引起局地降雨侵蚀力呈周期变化。

4 结 论

使用EOF法对长江流域186个雨量站1960—2015年日降雨量计算得到的降雨侵蚀力进行分析，提取其主要时空变化特征向量，采用统计方法分析其时空变化的主要特征，得出主要结论如下：

(1)长江流域1960—2015年多年平均降雨侵蚀力变化范围为114.423～16 233.136 MJ·mm/(hm2·h)，介于黄河流域和珠江流域之间，但其空间变化比这两者更为明显。降雨侵蚀力总体上从西北向东南递增，与经度和年均降水量呈正相关关系，与纬度和海拔呈负相关关系，与年均降水量相关性最强。

(2)EOF分析的前4个特征向量可以较好地解释长江流域1960—2015年降雨侵蚀力的空间分布特征，其中前2个为主要变化特征：模态第一特征向量分析结果表明1960—2015年间长江流域大部分地区降雨侵蚀力变化趋势具有高度一致性，下游地区降雨侵蚀力波动程度比上中游地区大；模态第二特征向量分析结果表明洞庭湖水系、鄱阳湖水系、四川盆地和长江上游局部地区降雨侵蚀力呈现与长江流域其他地区不同的震荡类型，长江中下游河段以北区域和鄱阳湖流域东南降雨侵蚀力变化较大。

(3) 长江流域降雨侵蚀力在1960—2015年间总体上以每年290.246 MJ·mm/(hm2·h)的速率增加，第一模态时间系数的极值与长江流域旱涝事件相对应，在1990—2010年呈现2～5 a的周期性波动，与区域干湿交替变化相关。