基于IDA方法的半刚接钢框架内填暗竖缝RC墙结构超强系数研究
2018-10-15孙国华
王 跃,孙国华,冯 进,魏 鑫
(1.苏州科技大学 土木工程学院,江苏 苏州215011;2.苏州科技大学 建筑与城市规划学院,江苏 苏州215011)
地震不可预测性导致建筑物的毁灭性破坏严重制约了人类社会文明的发展,所造成的建筑物破坏和倒塌是人员伤亡和财产损失的主要原因,如何提高建筑物的抗震性能是工程抗震领域的关键问题。一些学者尝试提出了具有优良抗震性能的新型结构体系用于减轻结构震害。孙国华等[1]对传统的钢框架内填钢筋混凝土剪力墙结构进行了改进,通过在实体RC墙上设置若干条未贯通的暗竖缝,提出了半刚接钢框架内填暗竖缝钢筋混凝土剪力墙结构(简称PSRCW)。在多遇或偶遇地震水准下,PSRCW结构的暗竖缝保持完好,可为结构提供较大的抗侧刚度,以抵抗地震水平侧向力;当遭受罕遇地震时,PSRCW结构的暗竖缝剪碎形成贯通竖缝,内填墙转化为若干个并联的缝间墙,内填RC墙的高宽比显著增大,缝间墙两端形成弯曲塑性铰,其变形能力及延性性能显著提高。PSRCW结构能够充分发挥暗竖缝RC墙的作用,表现出明显的两阶段受力特征,具备良好的抗侧刚度,易满足抗震规范的变形要求。近年来,对PSRCW结构的抗震机理、破坏模式、滞回性能、设计方法进行了深入研究[1-4],但尚未对此类结构的超强能力进行系统评估。
超强反映了结构的实际承载力大于设计承载力的程度,绝大多数正常设计和施工的建筑物均存在超强现象。用于定量衡量的超强系数是进行结构抗震设计的重要参数。国内外大量学者对不同结构体系的超强开展了系统的研究工作,Osteraas等[5]较早地使用Pushover方法对按美国UBC规范设计的抗弯钢框架结构的超强进行了系统研究,Jain&Navin[6]则采用Pushover方法评估了钢筋混凝土框架结构的超强能力。Balendra&Huang[7]综合评价了抗弯钢框架、中心支撑钢框架和半刚接钢框架结构的超强系数和延性折减系数。Stefano等[8]研究了超强对多层非对称结构抗震性能的影响,发现单层结构的超强系数非常小。Branci等[9]通过对4榀6层3跨钢筋混凝土框架结构进行静力弹塑性分析,研究了引起结构超强的原因及相关影响因素。国内学者李刚强[10]考虑设防烈度等因素,对5榀钢筋混凝土框架结构进行了推覆分析,给出了在不同抗震设防烈度下钢筋混凝土框架结构超强系数的建议取值。刘兰花[11]考虑设防烈度、结构层数、跨度等影响因素,研究了钢筋混凝土框架结构的超强性能。翟长海等[12]分别采用动力时程分析法和Pushover方法对4榀钢筋混凝土框架进行了分析,建议按我国抗震规范设计的钢筋混凝土框架的超强系数可取2.0。周靖等[13]分析了地震设防烈度、层数、填充墙等因素对钢筋混凝土框架结构超强的影响。韦锋等[14]对比分析了美国、加拿大、欧盟等国家抗震规范对结构超强的相关规定。赵风雷[15]研究发现混凝土柱的单边配筋率对钢筋混凝土框架结构的超强性能影响不大,材料强化和结构内力重分布会导致结构超强系数增大。张连河[16]建议按我国抗震规范设计的钢筋混凝土框架结构的超强系数最小值取为1.5。孙国华等[17]通过对半刚接钢框架內填实体RC墙结构试验试件的分析,明确此类结构的超强系数取值在2.95~3.33之间。周剑[18]研究了偏心支撑耗能梁段的超强系数。王树和等[19]分析了钢筋归并对结构超强的影响。崔双双等[20]分别给出钢筋混凝土框架结构在不同地震水准下的超强系数。李坤明采用数理统计方法给出半刚接钢框架内填实体RC墙结构的超强系数具有95%置信水平的单侧置信下限值在 3.24~4.63 之间[21]。
开展结构超强能力的研究对防止结构遭受强烈地震作用时的侧向倒塌具有重要意义,已有研究给出了不同类型结构体系超强性能的定量评估,明确了相关影响因素。但关于半刚接钢框架内填暗竖缝RC墙结构的相关研究尚未展开,本文主要考虑近场及远场地震动的随机特性、基于IDA方法量化此类结构的超强能力,为PSRCW结构的工程应用提供参考。
1 基于IDA方法量化PSRCW结构超强系数的基本方法
1.1 增量动力时程方法
增量动力时程分析简称为IDA方法,最早Bertero[22]于1977年提出,Comell[23]对其进行了大量的研究与应用,目前已列入美国FEMA365规范用于评估结构整体的抗倒塌能力。IDA方法是传统非线性动力时程分析方法的改进,逐渐被国内科研人员所采用,已成为评估结构抗震能力的重要手段。IDA方法是通过将地震动输入给结构,并将地震动幅值按一定比例调整,即将地震动调整至多重强度水平,分析结构在每一个强度水平下的结构响应,通过将分析的强度参数(IM)和对应结构的反应参数(DM)组合成一系列离散点,并将其连接成为“IDA曲线”。IDA方法本质是将单一的动力时程分析扩展为多级的增量动力时程分析,可全面考虑地震动各个要素的影响,能更真实、合理地评估结构在不同地震作用下的抗震能力。采用IDA方法评估PSRCW结构的超强性能,主要目的是考虑近场及远场的地震动特性,以及地震动在峰值加速度、反应谱值、持续时间等方面的差异所导致地震动的随机性,基于IDA方法从概率角度量化PSRCW结构的超强系数。
1.2 基于IDA方法量化PSRCW结构超强系数的分析步骤
PSRCW结构具有明显的两阶段受力特征,在内填墙的暗竖缝剪碎时达到峰值承载力,随后由于变形模式的转换,PSRCW结构在第二受力阶段具有稳定的水平承载力和良好的变形能力,能够充分体现PSRCW结构的优势。因此,基于PSRCW结构的受力特征,量化PSRCW结构在层间位移角达到我国《建筑抗震设计规范》(GB50011-2010)[24]规定的1/50限值时的超强系数。
文中对严格按照两阶段方法设计的10层8度PSRCW算例进行IDA分析,选取ATC-63建议的22条远场地震波和22条近场地震波,通过对44条地震波进行调幅获取每条地震波作用下的基底剪力(Vy)和顶点位移(Δ)关系曲线,即IDA曲线。通过对每条IDA曲线的分析结果进行处理,确定层间位移角达到1/50时所对应的“IM-DM”点,并将其作为评估PSRCW结构超强的“性能点”,提取此时结构的基底剪力(V1/50),按公式(1)计算PSRCW算例在层间位移角达到1/50时的超强系数。通过对PSRCW结构的IDA曲线分析,分别获得了在近场及远场地震作用下的两组PSRCW算例的超强系数(RΩ)样本值。采用数理统计方法分别计算两组PSRCW算例超强系数样本的概率密度分布曲线,并取置信水平为95%的单侧置信下限值为10层8度PSRCW算例的超强系数建议值。

式中,V1/50为PSRCW结构的层间位移角达到1/50时的基底剪力;Vd为PSRCW结构的设计基底剪力。
2 PSRCW算例模型与地震波选择
2.1 PSRCW 算例概况
所采用的算例为10层PSRCW结构,设防烈度为8度,设计基本地震加速度为0.2g,场地类别为II类。PSRCW结构的周边框架主要承担竖向荷载,梁柱连接采用半刚性节点。中间核心区域是由暗竖缝RC墙组成的筒体,设置于楼梯间周边,并作为主要抗侧力构件抵抗水平地震力和风荷载。PSRCW算例层高3.3 m,边跨跨度为7.8 m。混凝土强度等级C30,钢材选用Q345B。PSRCW结构的平面布置见图1,立面布置见图2。
采用两阶段方法对10层PSRCW算例进行设计,表1给出了PSRCW算例钢柱、钢梁主要构件的截面。表2给出了内填暗竖缝RC墙的具体尺寸。
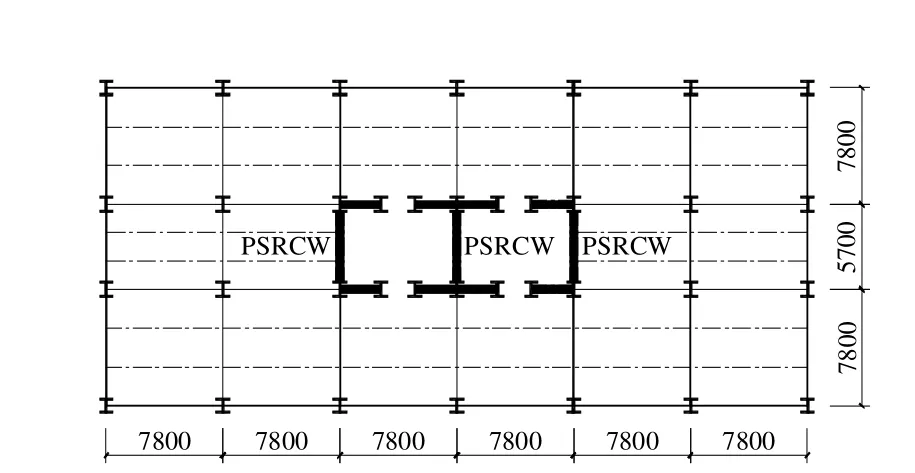
图1 10层PSRCW结构平面布置
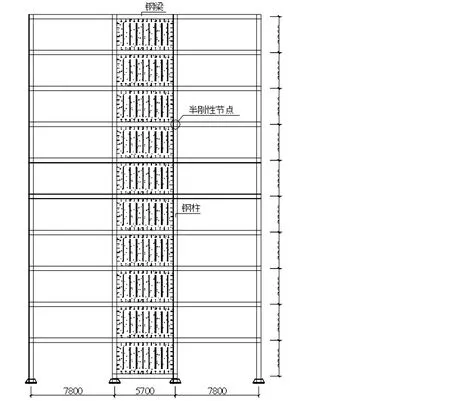
图2 10层PSRCW结构立面布置
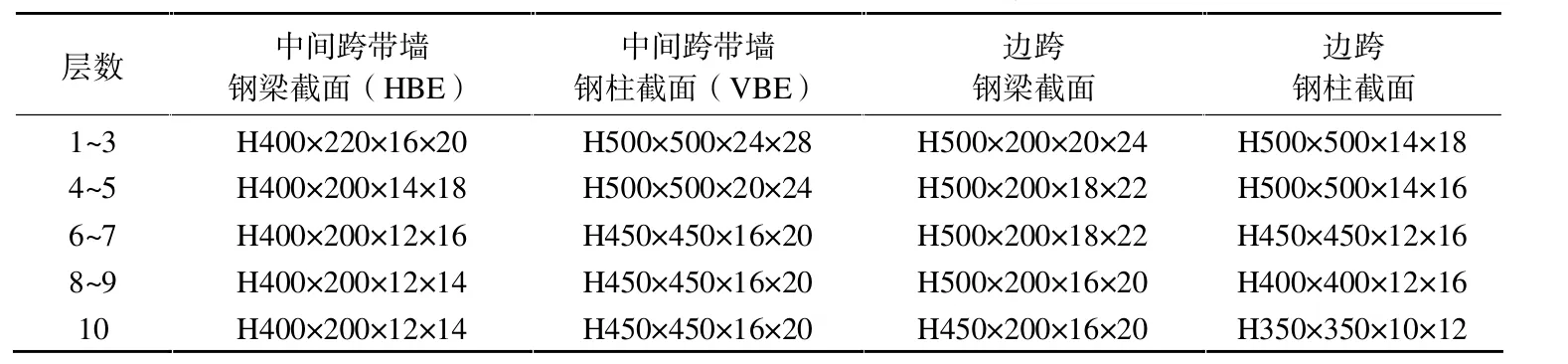
表1 10层PSRCW结构钢框架梁、柱截面
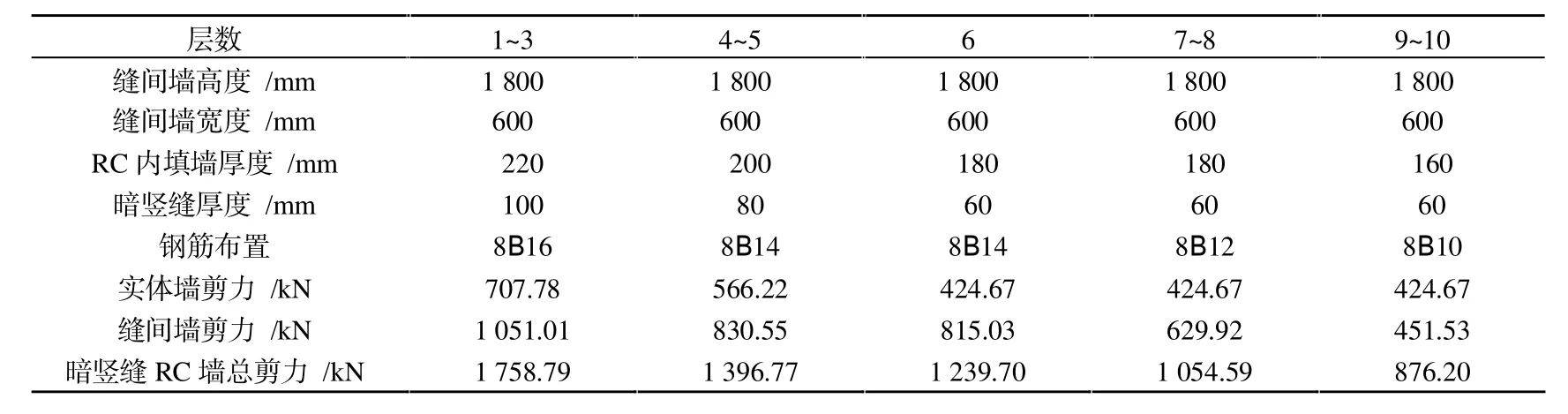
表2 10层PSRCW结构暗竖缝RC墙体的截面及配筋
虽然抗剪连接件设计是否合理对界面滑移影响较小,但对PSRCW结构的破坏模式有显著影响[25],本文忽略抗剪连接件的影响,假定抗剪连接件具有足够的水平抗剪承载力。PSRCW结构所采用半刚性节点采用简化方法进行设计,近似取半刚性节点塑性抗弯承载力等于钢梁塑性抗弯承载力的一半,它的转动刚度按公式(2)计算。

2.2 PSRCW结构的有限元模型
采用文献[25]提出的简化组合斜压板带模型,基于Perform-3D程序建立10层PSRCW算例的宏观有限元模型。其中,钢梁、钢柱采用纤维单元模拟,半刚性节点用转动弹簧进行模拟。暗竖缝RC墙采用组合斜压带简化模型,主要由两部分构成:(1)未贯穿的实体RC墙部分,采用主对角斜压带模拟暗竖缝RC墙体中未贯穿部分混凝土对其水平承载力的贡献;(2)缝间墙部分,采用纤维模型模拟缝间墙的混凝土及纵向钢筋贡献。图3所示为10层PSRCW结构的有限元模型。
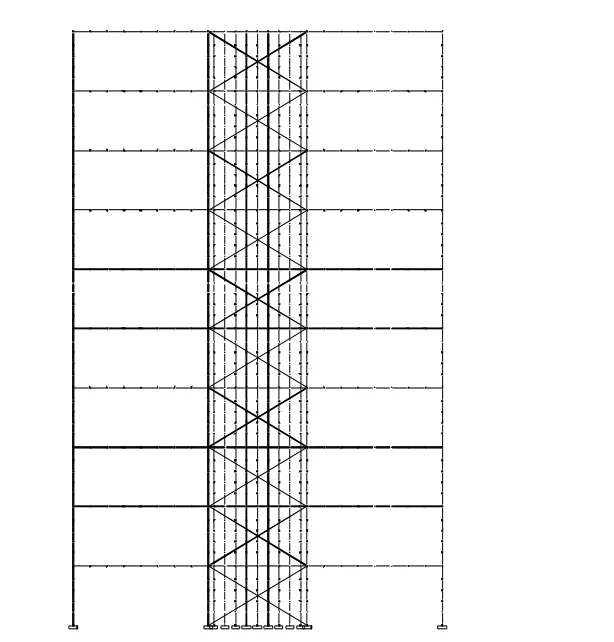
图3 10层PSRCW结构的有限元模型
2.3 地震波的选取
文中选取了ATC-63报告推荐的22条远场地震波和22条近场地震波,用于对PSRCW算例进行IDA分析。所选的两组地震波的β谱见图4。在进行PSRCW结构的IDA分析时,根据等步调幅方法分别对44条地震波峰值加速度按比例逐级加大,调幅增量为0.1g。
3 PSRCW算例的超强
3.1 PSRCW算例的IDA曲线
通过对10层PSRCW算例在44条地震波作用下的IDA分析,分别获得了PSRCW算例在远场和近场地震动作用下的基底剪力-顶点位移(Vy-Δ)关系曲线(见图5),由于所选择的44条远场与近场地震波具有随机特性,每条地震波作用下所获得的10层PSRCW算例的IDA曲线均不相同,即在相同顶点位移下每条地震波作用下所对应的基底剪力差异较大,由此确定的不同地震波作用下PSRCW结构的“性能点”也完全不同。
3.2 PSRCW算例的超强系数
根据IDA分析结果按公式(1)计算了10层PSRCW算例在共计44条地震波作用下在层间位移角达到1/50时的超强系数(RΩ,1/50),见表3。其中,Vd为设计基底剪力;PGA为层间位移角达到1/50时的地震波峰值加速度;V1/50为层间位移角达到1/50时的基底剪力。由表3可知,地震波的随机性导致按IDA方法分析获得的PSRCW结构超强系数离散较大,10层PSRCW 结构的超强系数在 1.91~3.24 之间。
采用Origin程序对10层PSRCW结构基于IDA分析所确定的两组超强系数样本进行了统计分析,分别给出了在远场及近场地震动作用下22个样本的频数统计直方图及拟合分布曲线,见图6。由图6可知,尽管10层PSRCW算例的超强系数样本点略少,但总体上仍近似符合正态分布,可采用数理统计方法量化其超强系数。
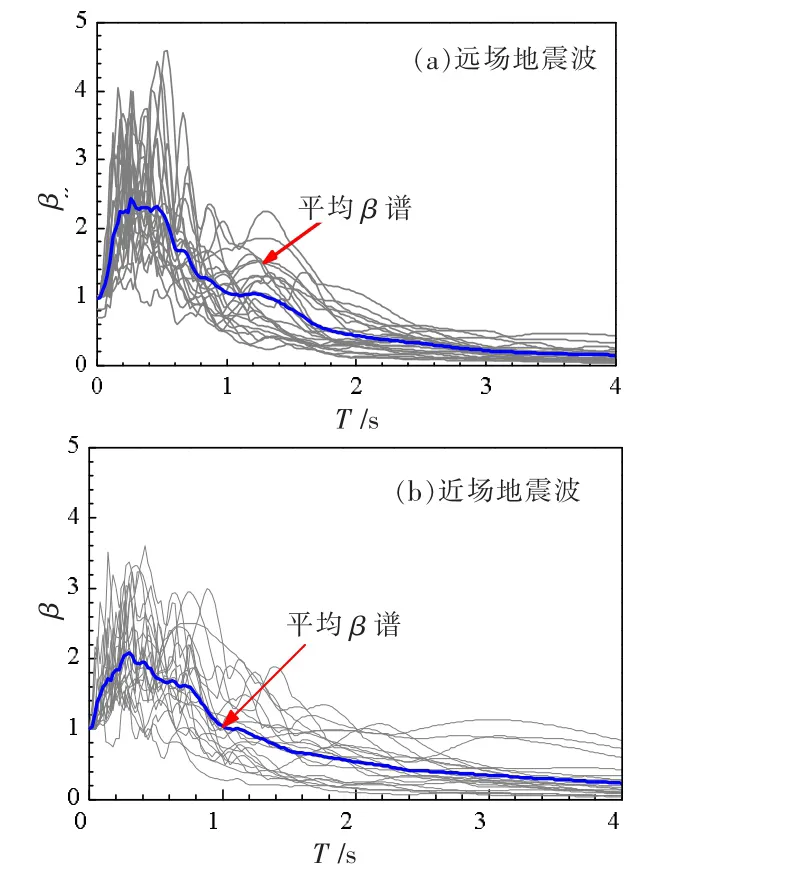
图4 两组地震波的β谱
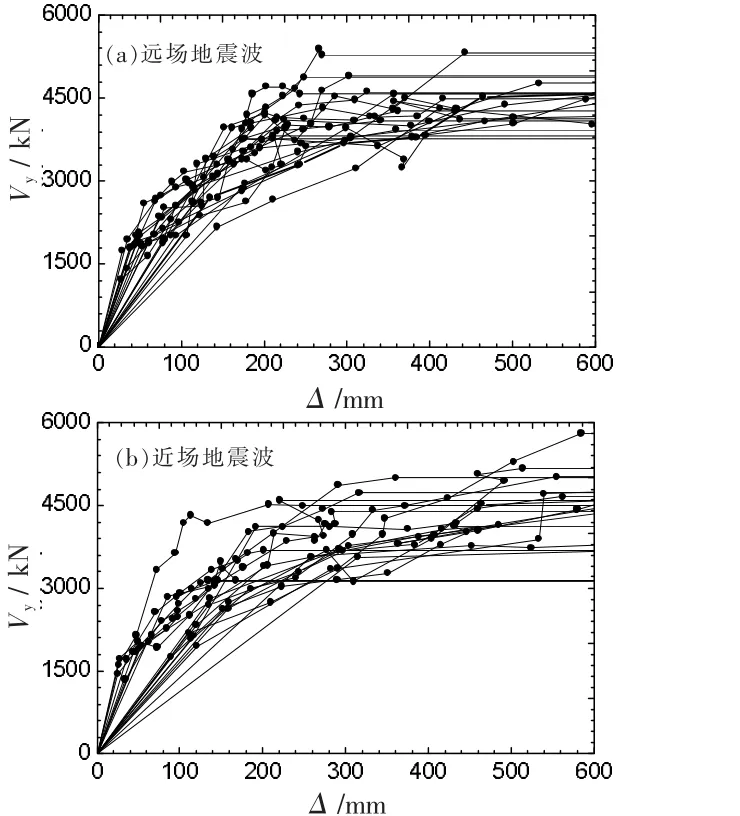
图5 10层PSRCW算例的IDA曲线
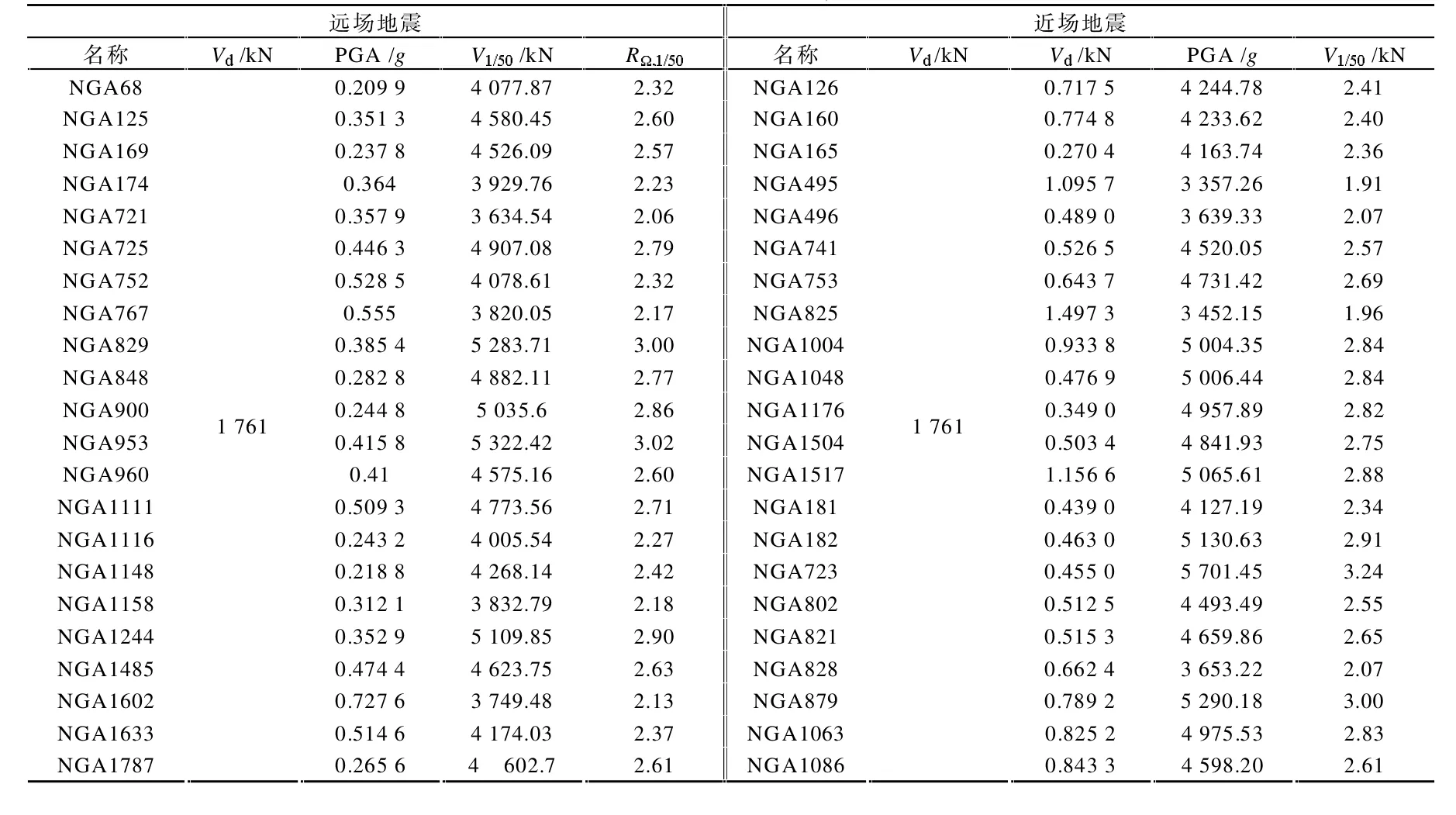
表3 PSRCW算例的 RΩ,1/50值
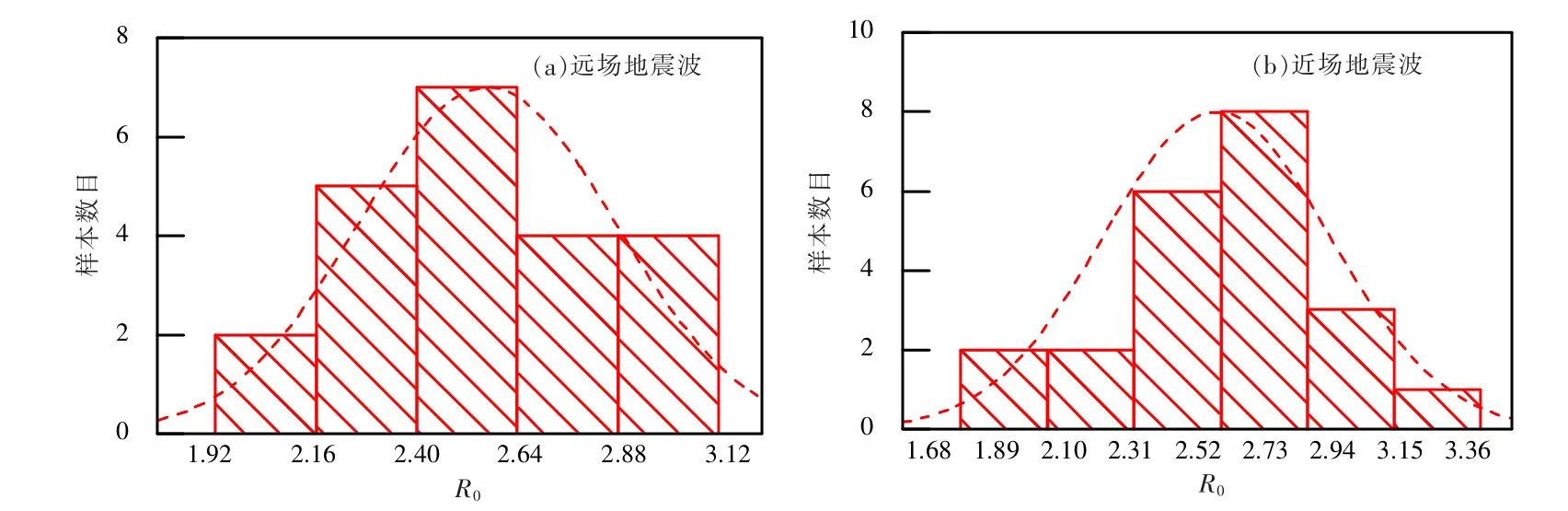
图6 PSRCW算例超强系数的频数统计直方图及拟合概率分布
根据数理统计方法对10层PSRCW算例的超强系数进行分析,取概率分布曲线上具有95%置信水平的单侧置信下限值作为10层PSRCW算例超强系数的代表值,表4给出了远场及近场地震作用下10层PSRCW算例的超强系数的最终统计结果。

表4 10层8度PSRCW算例的超强系数
由表4可知,10层8度PSRCW结构在22条远场地震波作用下基于IDA分析所确定的超强系数平均值为2.52,取其超强系数置信水平为95%的单侧置信下限为2.42。近场地震动作用下,10层PSRCW结构的超强系数平均值为2.58,由95%置信水平确定的单侧置信下限超强系数值为2.45,略大于远场地震作用下确定的超强系数值。地震波的近场速度脉冲效应及远场地震波的加速度循环效应对10层8度PSRCW算例的超强系数影响不显著,最终可建议10层8度PSRCW算例超强系数取2.4。
4 结论
对按两阶段方法设计了10层8度PSRCW算例,考虑了近场地震波的速度脉冲效应及远场地震波的加速度循环效应对其进行了IDA分析,基于概率统计方法确定了10层8度PSRCW算例的超强系数,主要得出以下结论:
(1)尽管所选择的两组地震记录样本数量略少,但所获得的10层8度PSRCW结构的超强系数仍近似符合正态分布;
(2)近场地震波的速度脉冲效应及远场地震波的加速度循环效应对10层8度PSRCW结构超强性能影响不明显;
(3)考虑地震动随机性,10层8度PSRCW结构超强系数具有置信水平为95%的单侧置信下限在2.42~2.45 之间,建议取为 2.4。
