履带式排爆机器人底盘双电机速度同步控制研究

沈 荣， 涂 朴， 黄 晨， 崔怀丰

(1.四川文理学院智能制造学院， 四川达州 635000；2.四川文理学院智能制造产业技术研究院， 四川达州 635000；3.达州市公安局， 四川达州 635000)

0 引言

近年来，随着恐怖主义威胁的加剧，排爆、侦察类机器人在警用、军事和公共安全领域的作用日益凸显，成为机器人领域的研究重点[1]。鉴于排爆机器人的作业环境复杂、严苛，因此常采用履带式底盘结构，该种结构具有越障性能好、转向半径极小、牵引附着性能强和良好的自复位性等特点[2]。

但是，由于编码器采样精度、机械误差、负载干扰、地面摩擦等因素的影响，导致电机在相同的控制输入下实际速度不相等，进而发生航向偏移、“走不直”等问题。为了解决这些问题，本文以排爆机器人常用的单节双履带式底盘作为研究对象，建立了运动模型，提出了不完整波形采样算法，减小了低精度码盘对闭环控制带来的不利影响。同时，运用基于继电器的PID自整定方法，确保机器人在运动过程中位姿保持稳定，控制性能良好。

1 运动模型分析

为分析履带式机器人的运动模型和位姿，从运动学方程开始建立模型。假设履带式移动机器人在二维平面中运动，不存在结构变形情况，即将其视为刚体运动。同时，不考虑动力学方程中着地压力、径向、侧向摩擦力等因素的影响。

图1为履带式机器人在水平面中的运动模型。假设履带式机器人左侧电机速度为vl，右侧电机速度为vr，l为履带底盘两侧履带的中心线间距，d为右侧履带比左侧履带多前进的路程。当机器人以O点为圆心，在两个相邻时刻Δt做圆周运动时，产生角度θ1和θ2。假定机器人初始航向与Y轴平行，由于机器人做圆周运动时相对于Y轴产生了偏离，形成航向角的变化量θ3。

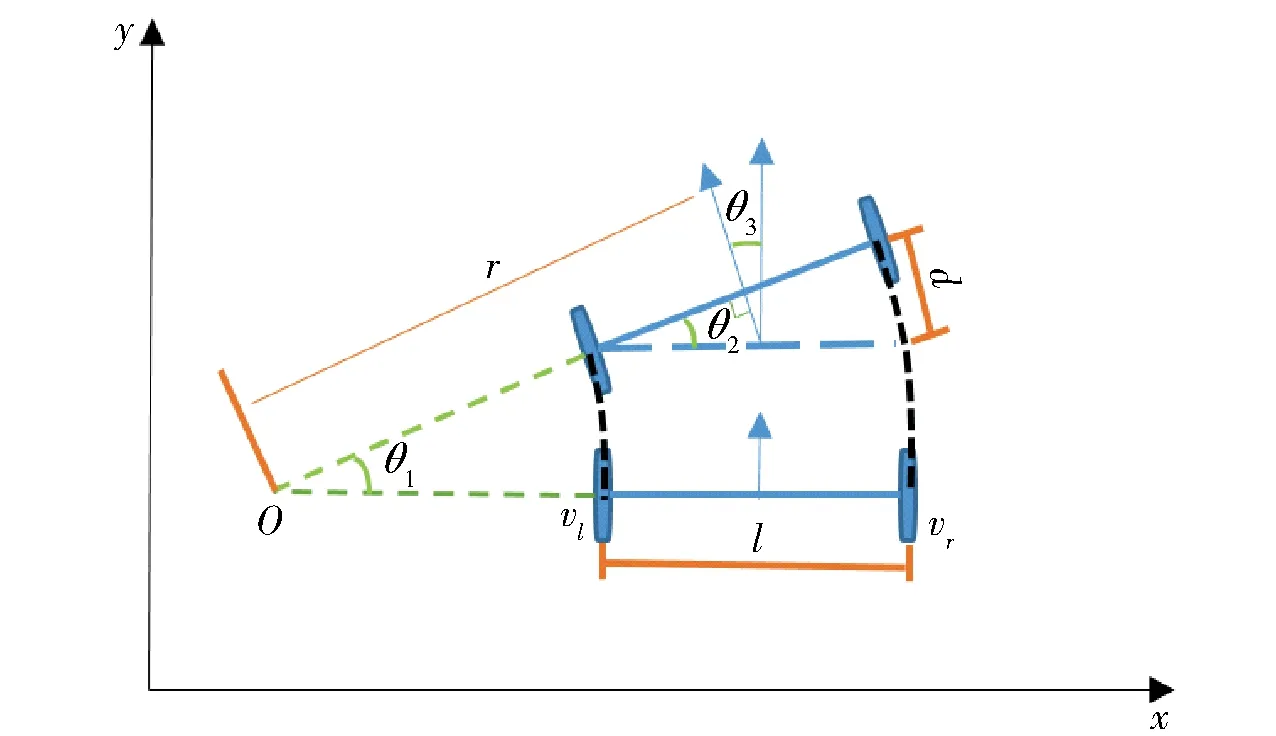
图1 履带式机器人运动模型

首先，根据速度瞬心法得到机器人的前进速度等于左右两侧履带速度的平均值：

(1)

然后，计算机器人的角速度ω。从图中的几何关系可以得到，航向角的变化量θ3=θ2=θ1。即机器人的航向角的变化量等于其绕圆心旋转的角度。同时，由于相邻时刻Δt很小，航向角的变化量θ2很小，可以推导以下近似公式：

进而得到机器人的角速度ω：

(2)

通过公式(1)和(2)，可以得到以下结论：当履带式底盘左右两侧的线速度相等，机器人做直线运动；履带式底盘左右两侧的线速度不相等时，则机器人做圆周运动，角速度由两侧履带的速度之差控制；当左右两侧的线速度绝对值相等，但方向相反，则机器人做原地旋转运动。

2 双电机速度同步控制策略分析

目前，保持多电机的协调运转常用两种方法：一种是机械方式，另一种是电方式[3]。机械方式虽然牢固可靠，但是容易形成多处误差积累。实践中，对机器人的电机同步控制多采用更加灵活的电方式。

在电方式中，主要有同等控制、主从控制、交叉耦合控制、虚拟主轴控制以及偏差耦合控制等[4]。由文献[5-6]可知，双电机同步控制通常采用主从控制、同等控制或交叉耦合控制。其中，同等控制方式是指两侧电机同时受到控制器控制，其本质是一种并行处理结构。该结构对两侧电机同时进行调节，不仅调试时间短，而且有利于机器人在启动、停止阶段保持同步。本文选取同等控制方式作为履带底盘电机的同步控制方式。

3 控制器设计

3.1 控制器系统框架

PID控制作为过程控制中应用最广泛的控制方法，因其方便、有效、可靠的特点，被广泛应用于工业控制和实验控制等领域[7]。本文运用位置式PID算法进行控制器设计。PID公式为：

(3)

控制系统的整体框架为：首先，在排爆机器人底盘电机上增加编码器，实时反馈电机速度。其次，将电机速度或者码盘计数作为闭环系统输入量，同时设定电机运行的期望速度或单位采样时间内的码盘采样脉冲数作为比较值。最后，经过PID计算，输出PWM值提供给电机执行。闭环系统框如图2所示。

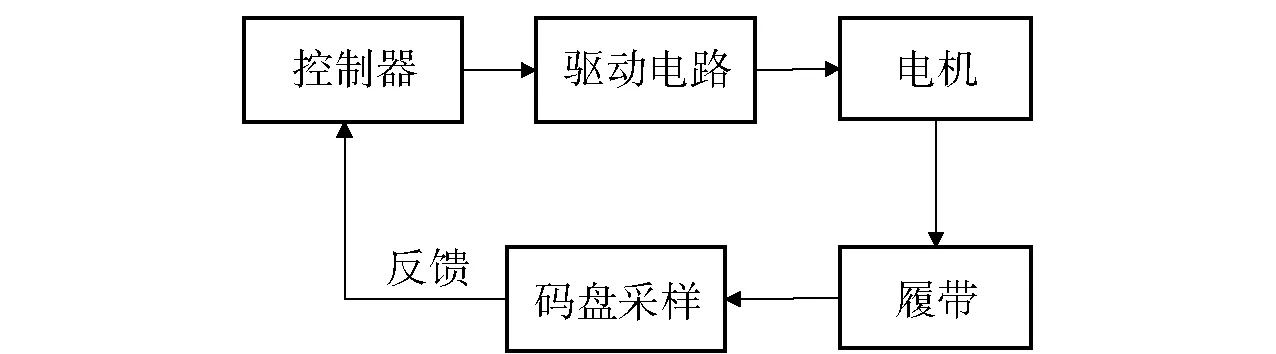
图2 闭环系统框图

3.2 不完整波形采样算法设计

对控制系统进行PID调节，一个必要条件即有可靠的输入量。对履带式底盘而言，采取一种可靠的方式进行测速是后续实现较好PID调速效果的先决条件。本文采用的测速方式是通过将一段时间内码盘采样脉冲数乘以每个脉冲对应的履带底盘移动距离的变化量，再除以时间，便可得到电机速度。电机速度计算可由下式表示：

Speed= Count×Precision÷Cycle

(4)

其中，Speed为电机速度，Count为脉冲个数，Precision为脉冲精度，Cycle为采样周期。如，假设履带底盘电机外轮直径80 mm，采用100齿/圈的光码盘，假设码盘每经过一个齿产生一个脉冲，则不考虑传动误差的情况下，单个脉冲对应的底盘距离变化为：80π/100≈2.513 3 mm。

显然，脉冲精度是采样中的关键环节。但是，在绝大多数情况下，一个采样周期内不会是恰好经过完整的脉冲个数，会出现在一个码盘齿中间某处尚未触发下降沿脉冲信号时，便已结束一次测速采样，并进行下一次测速。这造成了脉冲计数不准的情况发生，一个采样周期内会与实际值有所偏差。特别是在码盘精度不高的情况下，误差范围较大，这对于将来要进行PID调节来说是非常不利的。对此，本文提出了不完整波形采样算法。

其主要思想是：相邻两个脉冲的周期不会突变(排除干扰造成的脉冲丢失、多发现象)。 用计数和测周期两种方式组合，实现倍频，以提高分辨率。具体处理方式为： 在测速周期内，一方面对脉冲计数，得到完整脉冲的计数值。同时，测量每个脉冲的周期，保存上一个脉冲的周期值为计算非完整脉冲做准备。当测速周期到时，读取当前脉冲周期测量的“计时值”，除以保存的“前一脉冲周期值”，即可得到非完整脉冲值的占比，从而提高分辨率，如图3所示。

图3 不完整波形采样示意图

3.3 PID自整定算法设计

排爆机器人的作业条件较为复杂，既包含混凝土地面、砂石混合地面以及泥土地面等不同摩擦系数的通行情况，也可能发送负载变化。因此，履带底盘电机的闭环控制应具有一定的自适应性，以应对各种环境下的同步控制需要。结合继电器自整定方法，设计了相应的算法，主要思路是：

①稳定为先：先预调节PID参数，使系统的被调量和输出都达到稳态，并且被调量近似达到设定值。

②强行震荡：暂时禁用PID调节，使控制器将一个矩形波状的控制作用力作用于系统，当被调量低于设定值时，控制输出产生一个正的阶跃信号，迫使被调量向高处转变，当被调量高于设定值时，控制输出产生一个负的阶跃信号，迫使被调量向低处转变，由此强行使系统产生震荡。再通过测量峰值、周期，从而反映出这个系统本身的特点，根据这些值计算出合适的PID参数。

③分析波形：分析以上过程产生的波形的特征，根据需要计算出相应的PID参数。

④投入使用：将自整定得到的参数投入PID调节器中，即可让系统实现较好的PID调节效果。

图4 自整定算法流程图

4 控制器实现

控制器采用ATmega2560微控制板作为主控，并外接H桥电机驱动板、直流减速电机、编码器等设备。程序设计在Arduino IDE 1.6.13环境中完成。

4.1 不完整波形采样算法实现

底盘测速时，先利用单片机外部中断函数捕捉脉冲，同时通过不完整波形采样算法提高采样精度，最后将相关数据代入公式(4)计算。

测速函数主要程序代码段：

void Speed ()

{

halfPulseTime=micros()-tempTime; ∥最后一个不完整矩形波时间=触发定时器中断的系统时间减去上一个完整矩形波的系统时间

halfPulse=halfPulseTime/pulseTimeInterval;∥不完整矩形波换算成0.xx个完整矩形波=不完整矩形波时间除以完整矩形波时间

pulseInterval=YM.pulseSample()-pulseInterval;

∥定时测速周期内，采集的完整脉冲矩形波个数

speed=[1-halfPulseBefore+(pulseInterval-1)+halfPulse]×(2.513 3/2)/SAMPLE_DELAY×1 000;

∥速度=(上次不完整矩形波剩余部分+完整脉冲数+最后一个不完整波数)×每个脉冲对应的距离/测速毫秒时间×1 000

halfPulseBefore=halfPulse; ∥存储本次测速的最后一个不完整波数

pulseInterval=YM.pulseSample(); ∥记录本次测速周期结束时脉冲总数

}

4.2 PID自整定算法实现

按照PID自整定算法设计思路，按照“PID预调节、强行震荡、分析波形、投入使用”流程编写程序：

if (millis()<5 000) {

∥第一部分：PID预调节

} else if(millis()<10 000){

∥第二部分：强行震荡

} else { ∥第三部分：分析波形

while (caculateFlag) {

for (int i=1; i<20; i++) {

if (inputHistory[i]>inputHistory[i-1] && inputHistory[i]>inputHistory[i+1]) { ∥如果是波峰

inputHighAll+=inputHistory[i];

∥波峰值总数增加

inputHighNum++;

∥波峰个数计数增加

if(inputHighNum==1)atemp=i;

∥当产生第一个波峰的时候，atemp记录下此时是第几个数据

btemp=i;

∥当对20个历史数据分析完，btemp则可记录下最后一个波峰对应的是第几个数据

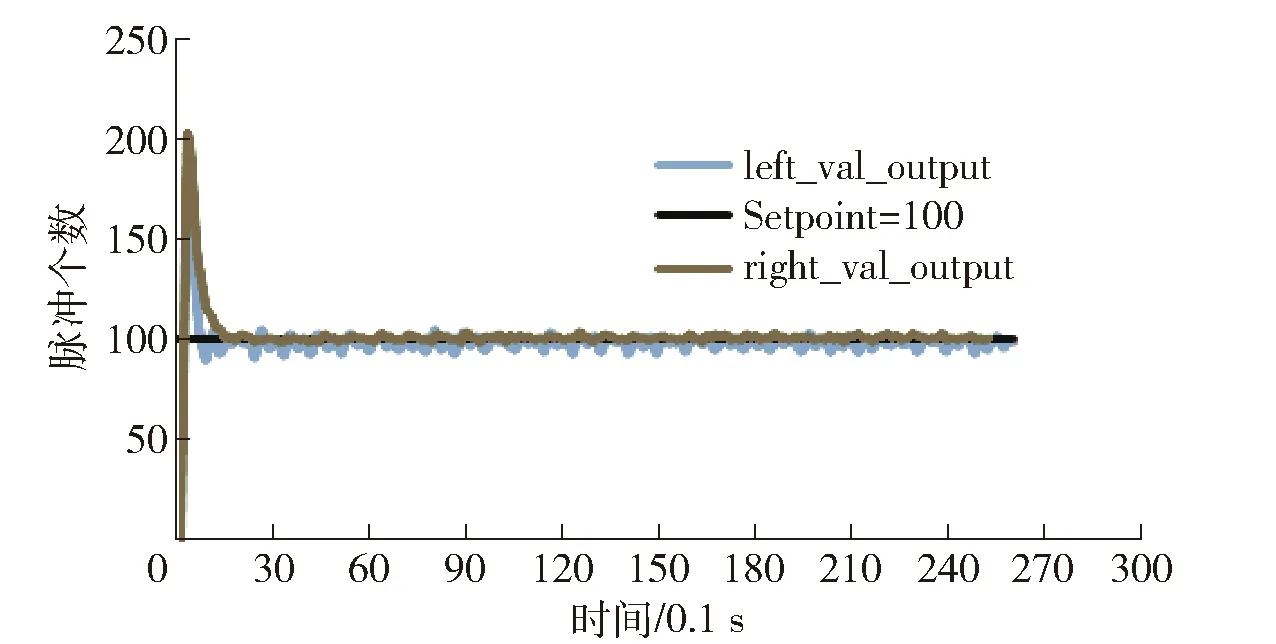
} else if (inputHistory[i]

inputLowAll+=inputHistory[i];

inputLowNum++;

}

}

float autoTuneA=(inputHighAll/ inputHighNum)-(inputLowAll/inputLowNum); ∥峰值的平均数A

float autoTunePu=(btemp-atemp)×0.1/(inputHighNum-1);

∥两个波峰之间的时间间隔Pu(s)

……

}

……

}

5 试验研究

5.1 不同算法下码盘采样结果比较

采用传统的测速方式，即不考虑不完整矩形波，会产生较大误差，不利于后续进行PID调节。使用不完整波形采样算法的情况下，给电机一个固定PWM信号，实际转速恒定时，测量得到的速度波形波动范围明显减小，克服了低精度码盘带来的影响，提高了分辨率。对比情况如图5所示。

图5 采样结果比较

5.2 不同速度下PID参数自整定测试

在混凝土地面情况下，采取PID参数自整定算法，通过设定单位采样时间内的码盘数值，对比不同速度下参数自整定运行的实际效果。

①采样周期为100 ms，期望值为100个脉冲，底盘速度约250 mm/s。PID参数自整定方法得到右侧电机参数：Kp=0.55，Ki=4.8，Kd=0.04；左侧电机参数Kpl=0.50，Kil=5，Kdl=0.04。如图6所示。

②采样周期为100 ms，期望值为150个脉冲，底盘速度约375 mm/s。PID参数自整定方法得到右侧电机参数：Kp=0.65，Ki=5，Kd=0.05；左侧电机参数Kpl=0.55，Kil=5，Kdl=0.04。如图7所示。

图7 速度设置为375 mm/s时PID自整定结果

在速度范围为200～500 mm/s内，本文进行了多组测试。由图可明显看出，系统反应迅速，达到稳定时间短，超调量较小，对输入无差跟踪。

5.3 系统整合测试

设置长度为4 m的直线通道，测试履带底盘两侧电机同步情况。采样周期仍为100 ms，两侧电机期望值均为100个脉冲，两侧编码器采样结果如图8所示。底盘在实际运动中航向偏移极小，基本保持直线运动轨迹。考虑到外部干扰以及电机机械转动的问题，剩余的些许波动可以忽略。运行轨迹如图9所示。

图8 左右两侧编码器采样结果

图9 履带底盘运行轨迹

6 结论

①双电机履带式排爆机器人运动方式为差速运动，角速度由两侧履带的速度之差控制。

②根据排爆机器人的需求分析，选取同等控制方式更有利于双电机底盘在启动、停止阶段保持速度同步。

③通过不完整波形采样算法，数据波动范围明显减小，减小了低精度码盘对闭环控制带来的不利影响，提高了采样精度。

④基于继电器方法的PID自整定方法，系统反应迅速，超调量小，有助于机器人在运动过程中保持位姿稳定，提高控制性能。