考虑风向分布的芝罘岛极值风速季节变化研究❋
2018-10-15林逸凡
林逸凡, 董 胜
(中国海洋大学工程学院,山东 青岛 266100)
风作为一种自然现象,其本身蕴含着巨大的能量,作为清洁可再生能源,风能的开发利用日益受到关注和投入[1-2]。沿海地区受陆风和海风的共同影响,风能资源相对内陆地区更加丰富[3]。观测、分析日常、极端天气条件下的风况在风能、航运、旅游业、渔业、城市空气污染控制规划等众多行业皆有直接的需求[4]。
风玫瑰图用于描述风速和风向的分布情况,是统计分析风气象要素最常用的资料。而实际工程项目对于数据挖掘分析日益充分、可靠性日益严格,在此要求下,采用概率联合分布模型分析风速风向分布更为准确,建立的联合概率模型可应用与和风气象要素密切相关的污染扩散[5]、风能资源评价[6-7],风电场布置[8-9]等领域,相比风玫瑰图用途更为广泛。
芝罘岛位于山东省烟台市西北约9 000 m海上,是我国最大的陆连岛,受季风环流及其他天气因素影响明显。本文基于角度-线性联合分布模型,提出利用风玫瑰图建立风速风向联合分布模型的方法,对芝罘岛各季节风玫瑰图建立联合概率分布模型,验证其可靠性。同时,基于条件概率理论,给出该联合分布模型随机数生成的相关算法,利用各季节风向风速联合分布模型采用蒙特卡洛模拟对各方位可能出现的极值风速进行了预测分析。
1 数据和方法
1.1 数据来源及组成
芝罘岛海洋环境气象监测站位置为37°36′N,121°26′E。收集得到该监测站根据1981—1986年风速风向观测数据绘制的春、夏、秋、冬四季节风玫瑰图(如图1)及其对应的风速风向频率统计表。统计表记录了16方位0~4级(0~7 m/s)、5级(8~10 m/s)、6级(11~13 m/s)、7级(14~17 m/s)以及8级以上(≥18 m/s)风力的频率,无风频率另记为C。另收集得到该测站统计的1981—1992年各月份、方位极大风速数据。
1.2 研究方法及模型
1.2.1 风速边缘分布模型 在海洋工程及风能领域,威布尔分布作为最常用的风速分布模型,适用性较强。考虑静风频率C不为零,常采用由Diracδ函数和Weibull分布组成的混合模型描述风速分布[10],其密度函数如下:
fV(v)=F0δ(v)+(1-F0)fW(v)。
(1)
式中:v≥0;F0=C为静风频率;δ(x)为Dirac函数,当x=0时δ(0)=1,当x≠0时δ(0)=0;fW(v)为威布尔分布密度函数:
(2)
式中,α,β>0分别为形状和尺度参数。
当v>0时,混合分布的累积频率函数为
FV(v)=F0+(1-F0)FW(v),
(3)
对式(3)进行变换可得
FW(v)=(FV(v)-F0)/(1-F0)。
(4)
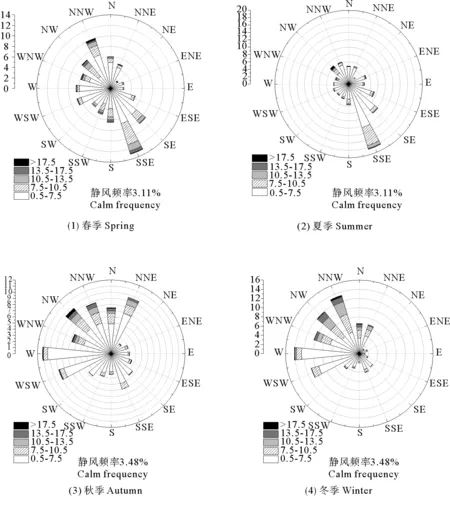
图1 芝罘岛四季风玫瑰图Fig.1 Seasonal wind roses of Zhifudao
令H表示可观测风(v>0),根据式(4),威布尔分布FW(v)可作为其分布函数HV(v)。设各级风力的风速上限集合为[Vi],i=1,…,5,其中V1=7,V2=10,…,V5设为23,由统计表可计算得到H的风速累积频率Pv,采用非线性最小二乘法(NLS)以累计频率均方根误差最小为目标拟合威布尔分布。
令Xi=ln(Vi),Yi=ln[-ln(1-Pvi)],α,β两参数的理论最小二乘估计值可根据下式(5)计算。由于V5为大致估计值,故式(5)计算的分布参数只能作为参数非线性最小二乘拟合的初始迭代值。
(5.a)
(5.b)
(5.c)
均方根误差指标显示各季度风速边缘分布拟合均良好。图2为各季度风速分布拟合图像。
1.2.2 风向边缘分布模型 von Mise分布为圆周上的正态分布,其混合分布fvMs(θ)可描述有多个主风向地区的风向分布,密度函数为
(6)
式中:θ∈[0,2π)为角度变量;N为von Mises分布的混合组数,Carta等[11]研究表明6组von Mise分布即可提供足够的拟合精度;wi>0为von Mise分布的权比例参数;0≤μi≤2π为位置参数;Кi≥0反映数据关于μi的离散程度,为集中度参数。I0(Кi)为零阶修正第一类贝塞尔(Bessel)方程,即
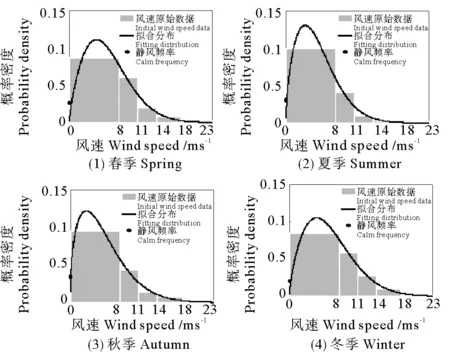
图2 四季风速边缘分布拟合图Fig.2 Fitting plots of the wind speed distribution for every season
(7)
令正北偏西11.5°方向为角度零点,风向值按顺时针计,由统计表计算H的各向风频pd,可观测风von Mises分布hΘ(θ)的参数采用边了解,边近似的两步拟合估计,具体步骤如图3所示流程图。图4为拟合得到的各季度可观测风(H)风向分布拟合图。
1.2.3 二维风速风向联合分布模型 Johnson和Wehrly[12]定义的角度-线性联合分布模型用于可测量风H,其密度函数为
hv,Θ=2πs(ψ)hV(v)hΘ(θ)。
(8)
式中:hv(v)和hΘ(θ)分别为H的风速及风向分布密度函数;ψ为风速风向相关系数。作为角度变量,通常采用两组von Mises混合分布近似其密度函数s(ψ)[11]。
(9)
对于总体风,当v>0时,联合分布的密度函数如下:
fv,Θ=2π(1-F0)g(ψ)hV(v)hΘ(θ)。
(10)
假设有一组完整风速风向数据集{(v,θ)},筛选出风向介于任意方位(θj,θj+1)之间,风速介于某级风力区间(vi,vi)的子数据集Cij。根据式(9),该组数据的相关系数ψ将在两个特征值ψ1到ψ2之间变化。而ψ1和ψ2的值又由HV(v1),HV(v2),HΘ(θ1),HΘ(θ2)共同影响。对于任意方位某级风力的可观测风频pij(i=1,2,…,16;j=1,2,…,5),由于HV(v)和HΘ(θ)的变化范围都不大,其ψ值的波动也不会很大,假设存在一个特征相关系数值ψij,则ψij和其对应的风频pij将共同对相关系数的分布产生影响。基于该假设,相关系数分布参数的估计采用以下方法:
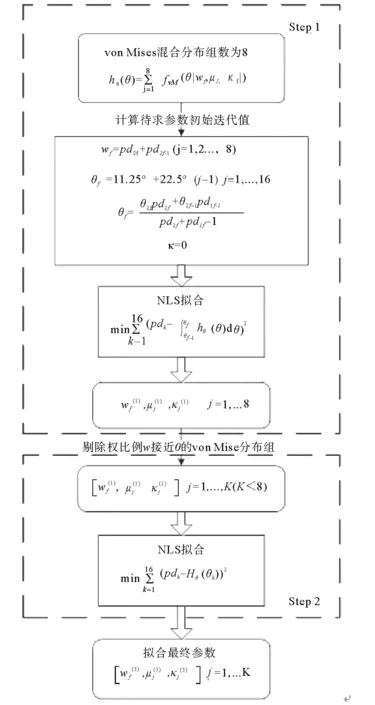
图3 风速von Mises混合分布拟合流程图Fig.3 Process map of the method to fit the von Mises distribution of wind direction
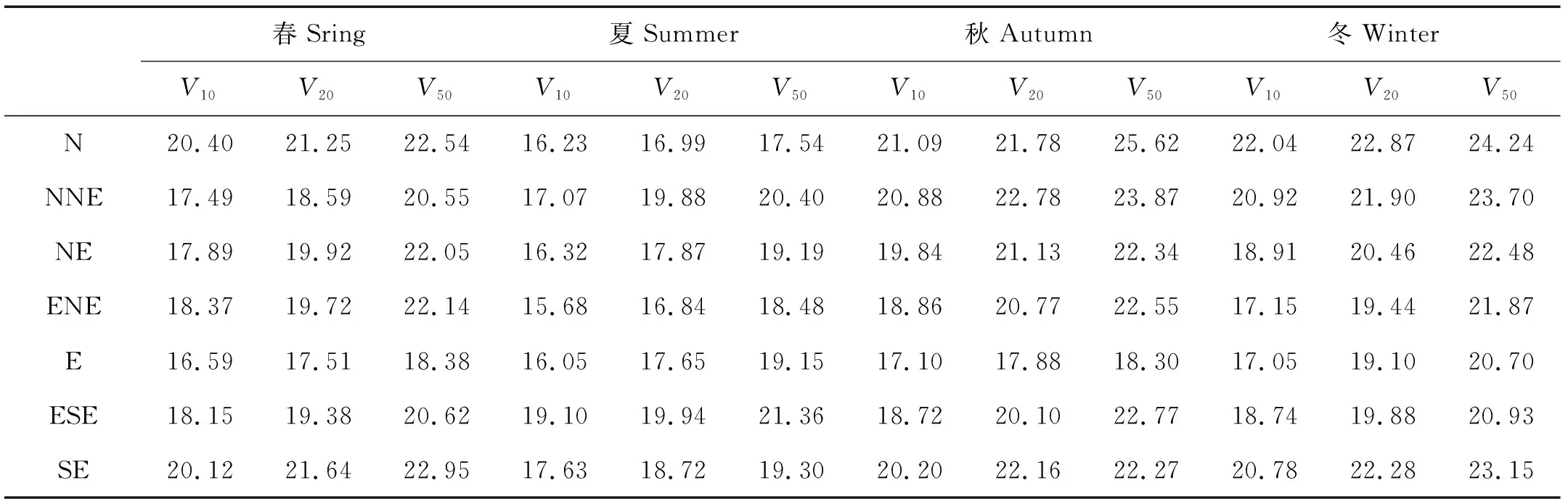
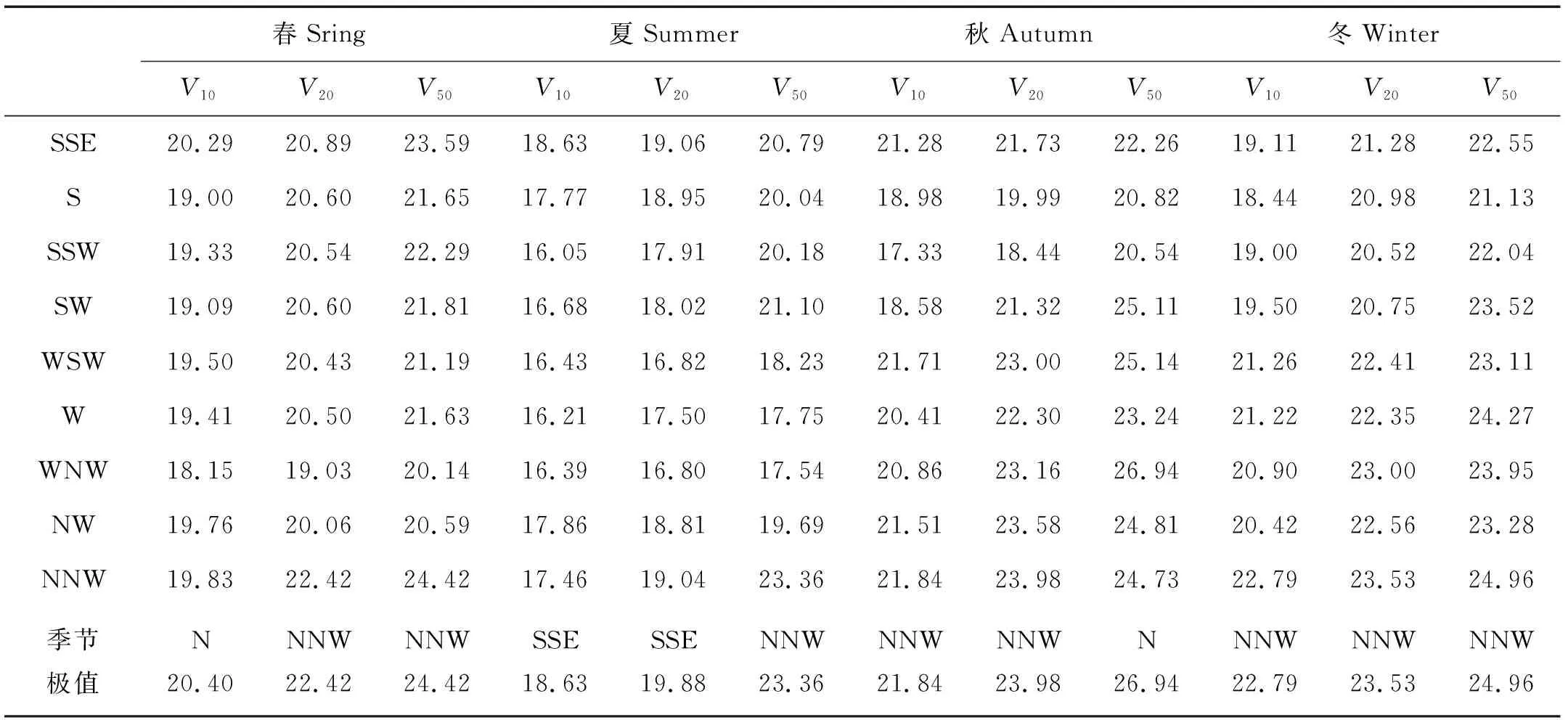
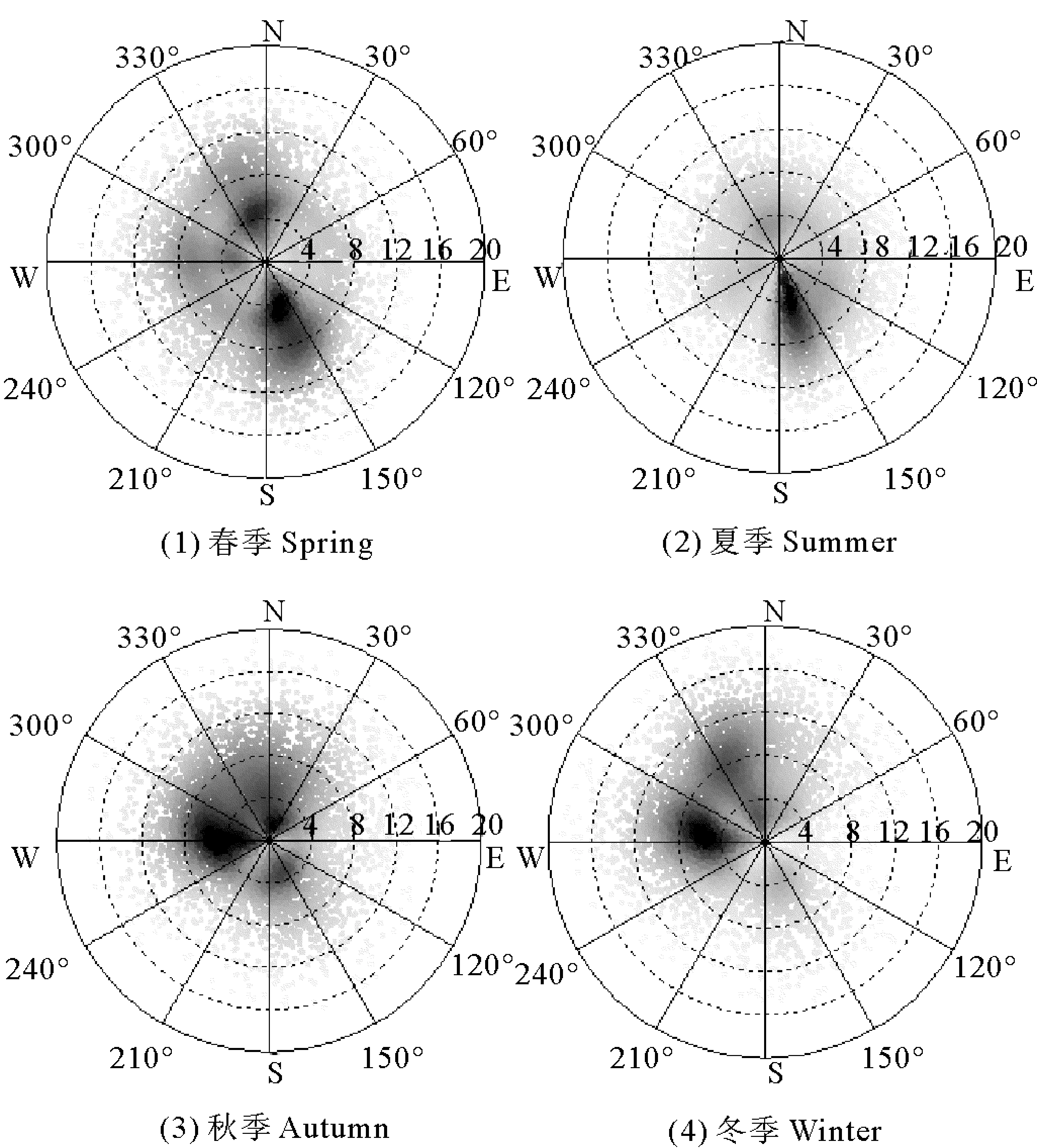
对于每个风向风速区间Cij(vi 图4 四季风向边缘分布拟合图Fig.4 Fitting plots of the marginal distribution of wind direction for foun seasons 利用拟合得到的风速威布尔分布HV,风向von Mises混合分布HΘ,风速风向相关系数ψ的von Mises混合分布s(ψ),结合已知的静风频率F0,最终得到各季度风速风向联合分布fV,Θ。 决定系数R2常用来反映模型与原始数据的相关程度,R2∈[-1,1],越接近1表示两者相关越强,当等于1时表示两者完全相关。计算公式如下: (11) 表1 芝罘岛各季节联合分布模型决定系数R2Table 1 Coefficients of determination R2 for Zhibudao in four seasons (①Cumulative frequency of theoretical joint distribution;②Cumulative frequency of original joint distribution;③Throretical frequency of wind rose diagram;④Original frequency of wind rose diagram.) 图5 各季度季风向风速联合分布拟合图 采用条件概率方法根据联合分布模型生成风向风速二维伪随机数[v,θ],算法流程图如图6。其中Fcondition(x)为当可观测风H风速累积频率HV=t时风向累积频率HΘ小于x的概率。 首先根据式(8)~(9),推导得 Hv,Θ=[G2(A)-G2(B)+G2(C)]/2π。 (12) 式中:A=2(HV;B=2((HV-HΘ);C=-2(HΘ,G2(·)为s(ψ)贝塞尔展开式的二重积分形式,按下式计算: G2(x)= (13) 图6 风速风向二维伪随机数生成算法流程图 式中,[wi,μi,Кi]为s(ψ)的von Mise混合分布参数。 令HΘ为定值等于t,HV=x,对式(12)求偏导数得到Fcondition(x),即 (14) 式中,G1(·)按下式计算: G1(x)= (15) 图7为拟合得到的各季节风向风速联合概率模型,按上述算法生成二维伪随机数散点图,其中灰度随数据点联合概率密度变大而加深。 采用蒙特卡洛法模拟100年各季度的风速风向数据,每组随机风速风向数据代表3 h平均值,筛选每年各季度中16个方位的极值风速,组成各季度、方位的极值风速序列,采用箱型图(包含:极小、25%、50%、75%、极大及异常值)对模拟极值风速数据进行统计分析,并与实测的芝罘岛地区1981—1992年各季节、方位极值风速数据进行比较,结果如图8。 3月份NW方位1981—1992年极值风速为40 m/s。实测数据点基本均位于各方位100年模拟数据上下分位之间,同时相当一部分位于上下四分之一分位范围,模拟得到的各方位年极值风速波动范围与实测资料吻合较好。将各方位100年极值风速模拟数据排序,根据其经验累积频率推测各季节、方位不同重现期下芝罘岛各季节方位极值风速值,如图9所示,结果如表2。 结合图7和表2分析,芝罘岛地区主要受三股季风影响,各季节风况变化明显。其中春季主要受NNW-N和SSE季风控制,极值风速方向为N-NNW,10、20和50年风速分别为20.4、22.4和24.4 m/s;夏季NNW-N季风减弱,主要受SSE季风影响,但50年一遇极值风速最大值仍出现在NNW,为23.4 m/s;进入秋季,W季风逐渐占据主导,但风速主要在8 m/s以下,极值风速仍为N-NNW,10、20和50年风速为21.8、24.0和25.6 m/s;进入冬季,虽然主风向为W向,但极值风速为NNW,10、20和50年风速为22.8、23.5和25.0 m/s。 图7 芝罘岛风速风向二维伪随机数散点图Fig.7 Scatterplots of the bivariate pseudo-random numbers of wind speed and direction Graphs at Zhifudao in four seasons 根据风玫瑰图数据对烟台芝罘岛地区四季风向风速联合分布建立模型,采用决定系数将风玫瑰图原始与理论数据进行比较,结果显示:联合累积频率和风频的决定系数大于0.9,表明根据风玫瑰图建立的联合分布模型与原始风玫瑰图相关性极强。同时,利用联合分布统计模型,结合蒙特卡洛法,模拟了该地区100年各季节风速数据,从中提取各季方位年极值风速,与实测数据比较表明:模拟的季节方位年极值风速数据可较好反映该地区极值风速波动范围,利用其对不同重现期风速方位极值进行预测估计。对于缺乏风速资料地区,可采用该方法分析通常及极端状况下的风况是一条有效的途径。 图8 芝罘岛四季方位极值风速模拟序列箱型图Fig.8 Boxplots of simulative seasonal directional extreme wind speed 图9 重现值-序号对应图Fig.9 Corresponding diagram of return value and sorted number 春Sring夏Summer秋Autumn冬WinterV10V20V50V10V20V50V10V20V50V10V20V50N20.4021.2522.5416.2316.9917.5421.0921.7825.6222.0422.8724.24NNE17.4918.5920.5517.0719.8820.4020.8822.7823.8720.9221.9023.70NE17.8919.9222.0516.3217.8719.1919.8421.1322.3418.9120.4622.48ENE18.3719.7222.1415.6816.8418.4818.8620.7722.5517.1519.4421.87E16.5917.5118.3816.0517.6519.1517.1017.8818.3017.0519.1020.70ESE18.1519.3820.6219.1019.9421.3618.7220.1022.7718.7419.8820.93SE20.1221.6422.9517.6318.7219.3020.2022.1622.2720.7822.2823.15 续表2 春Sring夏Summer秋Autumn冬WinterV10V20V50V10V20V50V10V20V50V10V20V50SSE20.2920.8923.5918.6319.0620.7921.2821.7322.2619.1121.2822.55S19.0020.6021.6517.7718.9520.0418.9819.9920.8218.4420.9821.13SSW19.3320.5422.2916.0517.9120.1817.3318.4420.5419.0020.5222.04SW19.0920.6021.8116.6818.0221.1018.5821.3225.1119.5020.7523.52WSW19.5020.4321.1916.4316.8218.2321.7123.0025.1421.2622.4123.11W19.4120.5021.6316.2117.5017.7520.4122.3023.2421.2222.3524.27WNW18.1519.0320.1416.3916.8017.5420.8623.1626.9420.9023.0023.95NW19.7620.0620.5917.8618.8119.6921.5123.5824.8120.4222.5623.28NNW19.8322.4224.4217.4619.0423.3621.8423.9824.7322.7923.5324.96季节极值N20.40NNW22.42NNW24.42SSE18.63SSE19.88NNW23.36NNW21.84NNW23.98N26.94NNW22.79NNW23.53NNW24.96 注:V10、V20和V50分别为10、20、50 a一遇极值风速预测值,单位为m/s。 Note:V10,V20andV50are 10, 20 and 50 a retura wind speeds, respectively, unit is m/s.
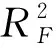
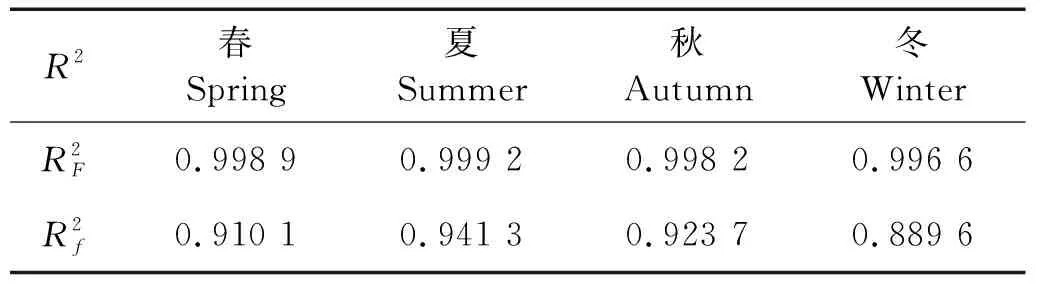
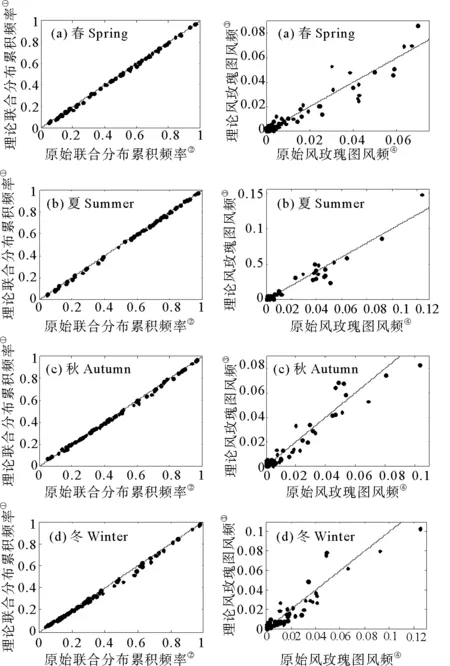
Fig.5 Seasonal Fitting results of the joint probability model2 芝罘岛季节极端风况蒙特卡洛模拟
2.1 随机数生成算法

2.2 年极值风速蒙特卡洛模拟
3 结语