基于Grey-GMDH的模块化实时潮汐预报❋

张泽国， 尹建川， 柳 成

(大连海事大学航海学院，辽宁 大连 116026)

实时精确的潮汐水位预报[1]对于船舶在沿岸水域和港口码头中的航行安全、港口码头的工程作业以及港口码头的水文勘测等方面具有重大的实际应用意义。随着电子航海的蓬勃发展，现代化的航海对潮汐水位的精确度要求日益增高。各种超大型船舶进出港口以及各种工程船在港口实施作业时，提供精确的潮位信息能够大大降低船舶搁浅、擦碰桥梁等事故的发生率。此外潮汐信息也一直是船舶航行计划制定和港口码头作业调度的重要影响因素。

调和分析法是潮汐分析预报方面最传统的技术，然而，调和分析法需要大量的长期观测潮位数据分析，才能够得到相对较准确的调和分析模型。但是由于长期的现场数据观测记录花费成本太高，因此一般很难得到这些需要的长期观测数据。而且调和分析模型的平均预报误差约为20～30 cm。另外，调和分析模型仅仅考虑了天体引潮力方面的影响而忽略了潮汐受到诸多时变因素非线性部分的影响，潮汐产生的原动力是天体的引潮力，但实际却受到诸如风力、风向、海水温度、气压等环境因素的影响，因此潮汐变化在该部分展现出强非线性和不确定性，传统的静态结构调和分析模型很难进行高精度以及实时的潮汐水位预报。

近年来，蓬勃发展的人工智能技术，如神经网络、模糊逻辑推理等技术，由于其较强的非线性映射和自学习能力，在工程计算领域得到了广泛的应用。基于误差反向传播的神经网络(BP)是当今最流行、最实用的一种神经网络，且在潮汐预报方面应用广泛[2-4]，尹建川[5]提出了利用序贯学习算法建立变结构的径向基神经网络的潮汐预报模型以反映系统的时变动态，Jain和Deo[6]使用神经网络进行了印度洋西海岸 New Mangalore潮位站的提前一天潮汐预报，并都取得了良好的预报结果。

GMDH[7](Group Method of Data Handling)全称为数据处理群方法，同时也被称为多项式神经网络。本文提出了一种基于灰色数据处理群网络模型的(Grey-GMDH)模块化潮汐实时预报模型。模块化是在分析解决某个具体问题时，把系统划分为具有不同属性的若干个模块的过程，在本文的潮汐预报研究中，依照潮汐的成因使用模块化方法将潮汐拆分为天文潮和非天文潮两部分，其中调和分析法用于天文潮部分的预测， Grey-GMDH预测模型用于预测具有较强非线性时变性的非天文潮部分。这种分块方式综合了两种方法的优势，即调和分析法能够实现长期、稳定的天文潮预报, 而 Grey-GMDH能够以较高的精度实现潮汐非线性拟合与预测。在本文的研究中，将灰色模型预测[8]方法应用于 GMDH潮汐预测中，从而减弱各种环境和天气等要素的不确定性以及非线性对潮汐水位预报精度造成的不利影响。最后选取 San Diego港口的实测潮汐数据进行港口潮汐的实时预报仿真，仿真实验结果表明本文提出的方法可以有效地实现潮汐预报的精确预报，并拥有较高的预报精度。

1 调和分析法

潮汐是海平面周期性上升和下降运动。潮汐产生的原因主要是天体的引潮力的作用，即天体的引力和地球-天体相对运动所需的惯性离心力的向量和。实际应用中最通用的一种方法就是调和分析法[9]，它将复杂的潮汐分解成若干周期性变化的部分。根据实际观测的潮位数据进行分析，可以求得潮汐调和模型中的各个常数。然后再根据得到的潮汐调和常数计算分潮组成的大小，并且可用来推算潮汐。理论上，潮汐的组成部分是复杂的，潮汐的分潮数量是众多的，但是在工程计算上，当分潮的平均振幅相对较小和分潮的格林尼治迟角相对较小时，有相当一部分的潮汐分潮成分是可以忽略的。在实际应用计算中，某地实际潮位高度可表示为：

(1)

其中：H0为分析期间的平均海面高度；n为潮汐分潮数量；hk为分潮的振幅；ωk和φk分别是分潮的频率和相位。

2 数据处理群网络模型

2.1 数据处理群方法(GMDH)

GMDH网络是一种基于启发式自组织原理的学习机器，由乌克兰科学家Ivakhnenko AG在1967年提出。它属于前馈型神经网络中的一种常用于预测[10-11]的局部型神经网络。不同于传统的误差反向传播神经网络(BP)，它的特点是网络结构不是固定的，而是在仿真训练过程中不断变化的，可以称之为变结构型神经网络。GMDH是一种基于进化计算的技术，它根据输入变量的维数、网络模型的结构和网络参数进行一系列的进化、遗传、变异和选择操作。典型的训练后的GMDH模型如图1所示。

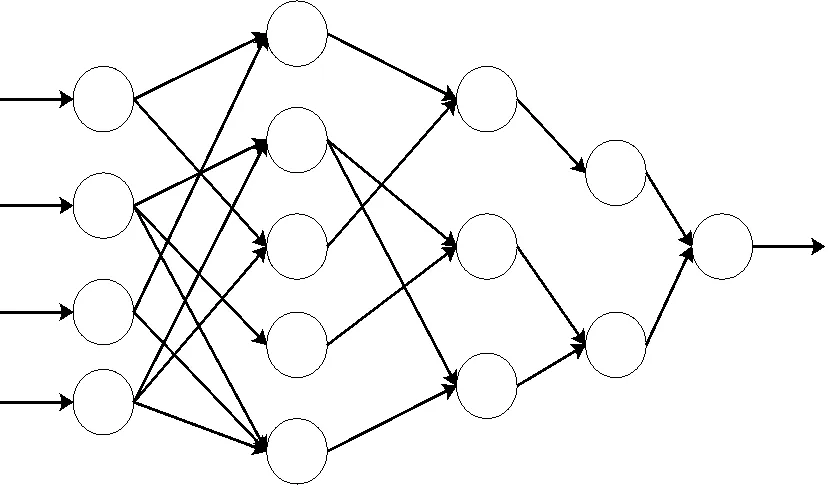
图1 GMDH网络结构示意图Fig.1 Structure diagram of GMDH network

通常GMDH网络的输入和输出变量之间的一般关系可以通过一个复杂的离散形式的Volterra泛函级数形式表示：

(2)

其中，式(2)即为Kolmogorov-Gabor多项式。X=(x1,x2,x3,…,xm)为模型输入向量，y为输出变量。这种形式的数学描述，可以表示由一个系统的部分二次多项式组成的只有2个变量(神经元)的形式：

(3)

GMDH网络模型的训练过程包括从输入层开始构建网络框架，调整每一个神经元的连接权值并逐步增加网络模型的神经元层数。在整个网络中，通常采用带非线性二阶预处理器的自适应线性原件[12](Adline)作为网络中神经元的传递函数。网络权值即为自适应线性原件多项式的系数。并使用基于Windrow-Hoff学习规则进行权值更新。第一层的神经元个数由输入变量的维数确定。若假设网络只有一个输入变量，输入层则只有一个神经元。则在t时刻的权值向量可表示为：

ωt=[ω0,ω1,ω2,ω3,ω4,ω5]T，

(4)

变量输入：

(5)

权值更新：

(6)

其中：α为网络学习率，通常取值[0.1,1]；ydt为网络的实际输出值。

2.2 灰色数据处理群方法(Grey-GMDH)

邓聚龙教授在1982年提出了灰色系统理论，灰色理论主要用于研究数据较少、信息较缺乏的不确定性问题。灰色系统理论以“部分信息已知，部分信息未知”的“小样本” 、 “贫信息”不确定性系统为研究对象，通过对“部分”已知信息的生成、开发，获取有价值的信息，从而完成对系统运行行为、演化规律的正确描述和有效监控[13]。对于传统的实现序列预测方法，经常需要大量的数据用于预测，然而灰色模型已经被前人证明，在处理不完全的信息以及成因不明确的问题时，它具有有效的算法来处理这些数据。灰色数据处理群模型处理数据须通过以下三个步骤，首 先 通 过 累 加(Accumulated Generation Operation，AGO)处理原始数据集，然后利用 GMDH对累加的数据进行预测仿真，最后通过反向累加运算(Inverse Accumulated Generation Operation, IAGO)进行数据还原得到整个模型的预测输出值。

3 模块化潮汐预报

按照潮汐成因的不同，潮汐预报组成可以分为两个部分，其一为天文潮影响部分，其二为非天文潮影响部分。天文潮部分主要由天体引潮力引起，具有明显的时变特征；非天文潮部分受到气象水文因素影响而产生，其变化没有明显规律且展现了很强的非线性。 因此天文潮和非天文潮部分存在较大区别，仅使用调和分析法或GMDH 预测的单一方法可能无法体现潮汐的完整规律[14]，并且预测结果会出现相对较大的误差值。针对以上情况，本文采用了一种 GMDH网络的模块化潮汐预报模型，该模型由调和分析法以及 GMDH两个模块组成，其中调和分析法用于天文潮部分的预报，GMDH则用于非天文潮部分的预报。该模型首先利用调和分析法预测潮汐的天文潮部分，获得潮汐的整体变化规律，再利用GMDH对非天文潮部分进行预测，修正预测结果，达到精确预报潮汐的目的。在 GMDH模型部分，灰色模型主要用于训练仿真数据的预处理和还原。具体的模块化结构框图如图 2 所示。

图2 模块化结构框图Fig.2 Structure diagram of modular

实测潮汐数据y(t),y(t-1),…,y(t-N)设置为模型的预测输入用于模块化预测模型。因调和分析预测模型可以进行长期的潮汐预报，其中,yH(t),yH(t-1),…,yH(t-N)为调和分析模块得到的潮汐预测值，yR(t),yR(t-1),…,yR(t-N)为y和yH两者的差值。潮汐的主要成因是天体的引潮力，调和分析法考虑的对象即是天体对潮汐的影响，所以实测值 与调和分析法预测值之间的剩余值可看作潮汐值受风力、风向、温度和气压等各种非确定性、非线性因素影响的非天文潮部分。由于非天文潮部分展现出较强的非线性和不确定性，采用灰色模型进行处理可以有效提取数据中的实用信息缓解不确定性。将连续k小时的灰色潮汐数据输入于GMDH网络中，再通过GMDH预测求得的结果即为k+1小时的潮汐水位预测值。

4 仿真结果与讨论

4.1 潮汐数据分析

相关性分析[15]的概念起源于信号的处理分析，相关性分析表现出时间序列中任意两个值之间的相关性是如何随着时间间隔而改变的，而自相关分析则刻画了时间序列相邻变量之间的相关性。自相关与偏自相关函数图[16]则是分析处理复杂时间序列问题的一种有效途径：自相关函数描述了时间序列数据相邻变量之间的关联性，偏相关函数则是剔除了中间变量的影响，准确地反映两个变量之间的关联性，并且二者紧密相连。潮汐水位时间序列受到诸多不确定性因素的影响，比如风力、风向、气温、气压等非线性不确定要素。这些不确定要素难以使用仪器设备进行精确测量，从而难以精确计算出每个要素对潮汐水位产生的影响。因此，使用相关分析法进行潮汐水位时间序列值之间的相关性分析，进而确定出Grey-GMDH预测模型的预测输入维数。选取0.5的自相关值和偏自相关值为标准确定系统输入维数。相关性分析结果如图3、4所示；由图3可以分析出潮汐数据的自相关系数拖尾，且其自相关系数逐渐向零靠近趋于稳定，同时说明潮汐的时间序列为平稳时间序列。由图4可以分析出潮汐数据的偏自相关系数4阶截尾。综上表明在t时刻的潮汐值与t-1到t-4时刻之间的潮汐值有着显著的相关性，因此可以选择前4个连续采样时刻点作为模型的预测输入维数。本次仿真实验选用San Diego潮汐站点共6 000组实测潮汐水位的数据进行仿真训练和预测，前4 200组数据作为模型的学习训练数据，剩余1 800组数据则用于模型的仿真测试数据。实测数据均为等间隔采样，采样间隔为每小时。本次仿真实验的实测潮汐数据可从网站http://co-ops.nos.noaa.gov上下载。

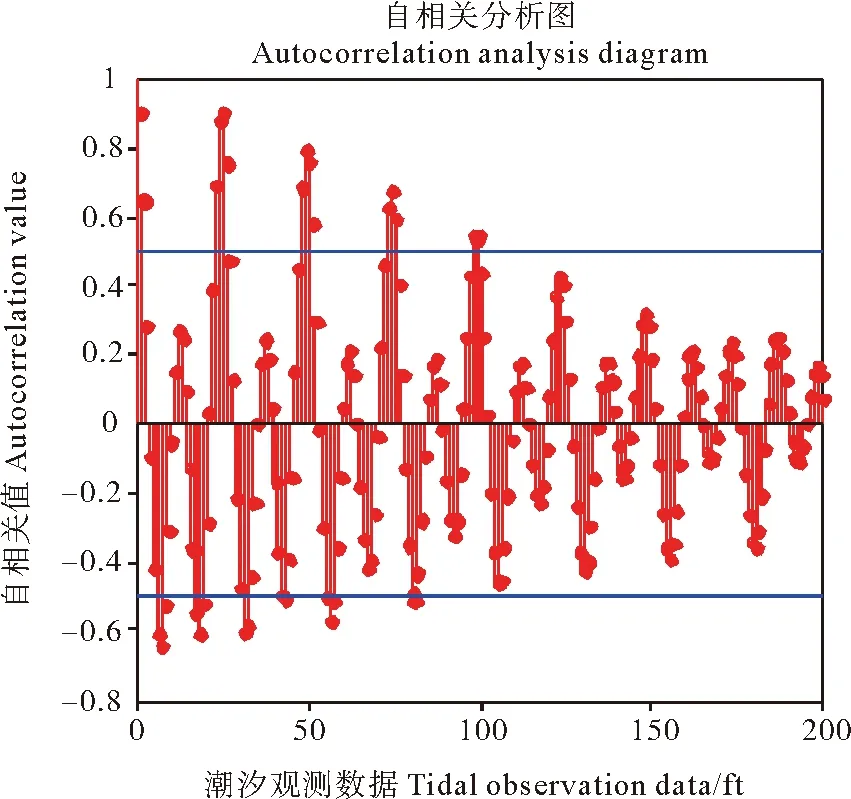
图3 潮汐数据自相关分析图Fig.3 Autocorrelation analysis of tidal dat

图4 潮汐数据偏自相关分析图Fig.4 Partial autocorrelation analysis of tidal data

4.2 调和分析模型的潮位预报

如图5所示：潮汐的预测值与实测值之间的变化趋势基本是吻合的，但是两者之间的误差也是相当明显的，引起潮汐水位的变化的原因是很复杂的，然而调和分析模型仅仅考虑了天体引潮力线性影响部分，而忽略了由各种不确定性因素引起潮汐水位变化的非线性部分。图5中的误差图可以看出，调和分析模型预测误差变动范围为[0.1,1]之间。调和分析的误差分布直方图显示：该模型的预测误差分布中心集中在了0.4左右，而没有趋于零。并且调和分析预测模型也出现了较大的预测误差值。

4.3 GMDH模型的潮位预报

图6为GMDH模型的直接仿真预测图。从GMDH仿真图中不难看出，GMDH模型的潮汐预测值与实测值之间的吻合程度明显优于调和分析模型。从图6中的误差图可以看出，GMDH模型的预测误差变动范围为[-0.4,0.4]之间。GMDH模型的误差分布直方图则表明：该模型的预测误差分布中心基本上集中在了0左右，但是误差分布不均匀，误差波动较大。并且GMDH预测模型也出现了相对大的预测误差值。

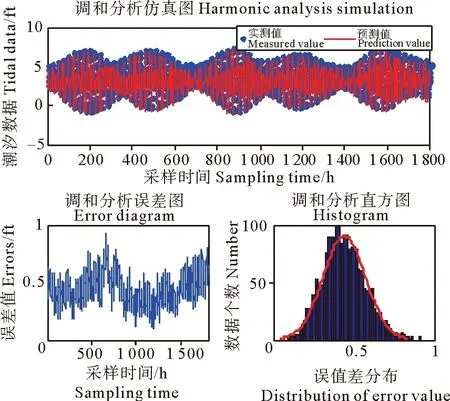
图5 调和分析仿真图Fig.5 Simulation results of harmonic analysis model

图6 GMDH仿真图Fig.6 Simulation results of GMDH model

图7为模块化的GMDH仿真预测图。由图7中的误差图可以看出，模块化GMDH模型的误差值基本上稳定在了[-0.3,0.3]之间，预测精度相对于GMDH直接预测模型和调和分析预测模型有了明显提高。而且由图7中的直方图可以分析出：模块化GMDH模型的预测误差分布逐渐趋于均匀平稳，误差分布中心基本趋于0，且误差分布相对于分布中心逐渐左右对称。

4.4 Grey-GMDH模型的潮位预报

图8为模块化Grey-GMDH仿真预测图。该模型的潮汐预测值和实测值几乎完全吻合。由其中的误差图可以分析得到：模块化Grey-GMDH模型的预测误差值稳定在[-0.2,0.2]之间，由图8中的误差分布直方图可以看出：模块化Grey-GMDH模型的预测误差分布中心几乎完全趋于0，误差分布更加均匀，且相对于误差分布中心几乎完全左右对称；误差分布范围相对于前三种模型明显减小。

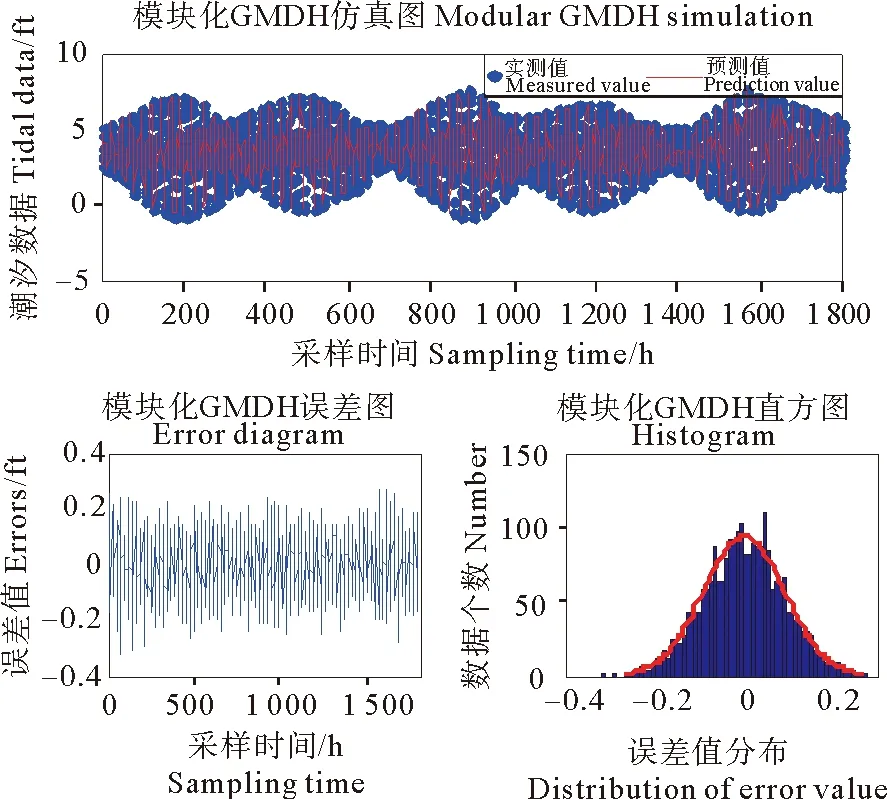
图7 模块化GMDH仿真图Fig.7 Simulation results of modular GMDH model

图8 模块化Grey-GMDH仿真图Fig.8 Simulation results of modular Grey-GMDH model

为了进一步定量分析本文提出的模块化Grey-GMDH预测模型的预测性能指标，给出各种预测模型详细的仿真预测结果如表1所示，所有的仿真环境以及参数设置均相同。

从表 1 中可以分析出，在数据处理群网络的基础上添加灰色模型处理数据后，使得潮汐水位的预报精确度相对于其他几种预测模型有着显著的提高。

4.5 Grey-GMDH预测模型的泛化能力和实用性

为了进一步验证模块化Grey-GMDH预测模型的泛化能力和实用性，选择美国西海岸四个港口的实测潮汐水位数据作为测试数据库，在相同的仿真条件以及相同的仿真实验环境下分别运用调和分析模型和Grey-GMDH模型进行仿真实验。实验结果如表2所示。

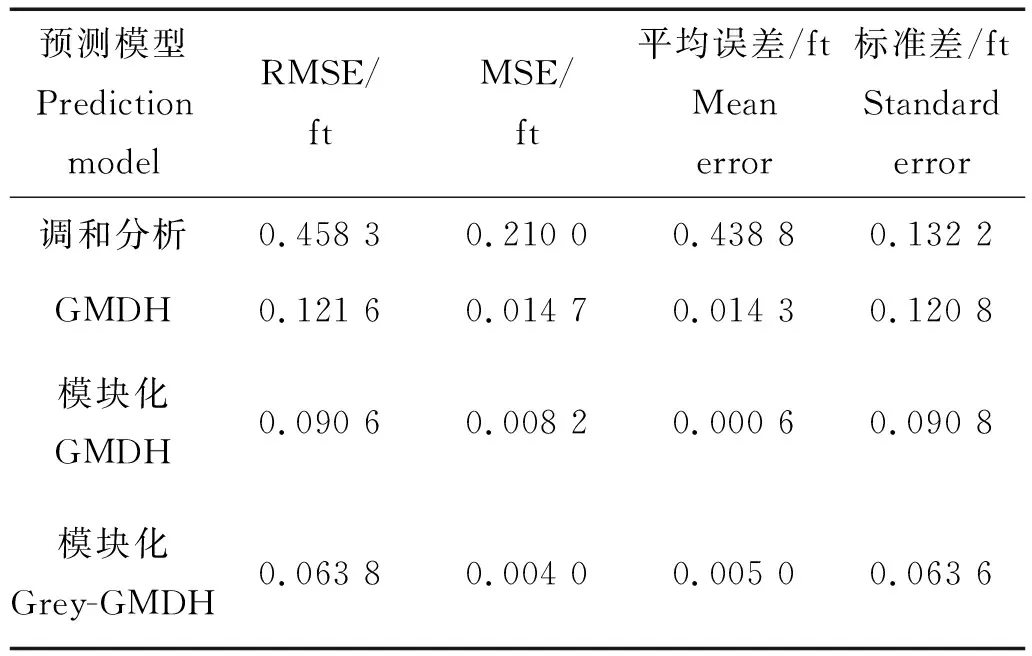
表1 预测结果Table 1 Prediction results

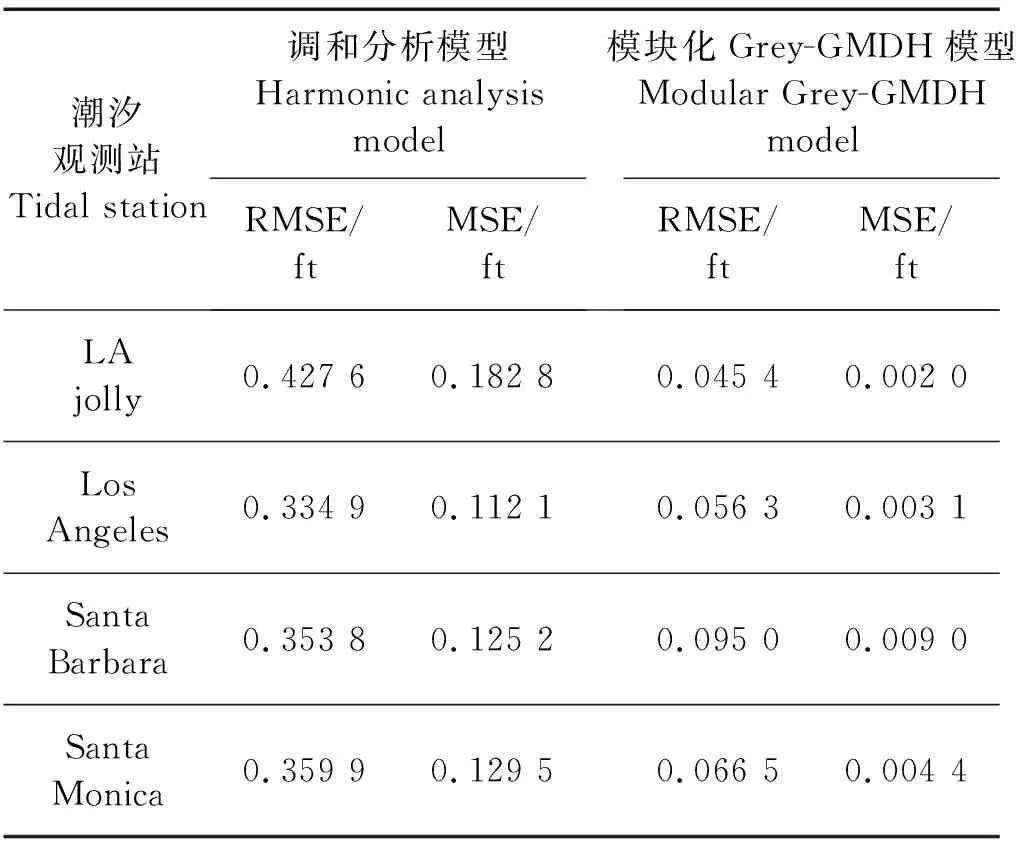
表2 仿真实验结果Table 2 Simulation results

从表 2 中可知，选用不同地理位置潮汐站点的潮位数据进行仿真实验，实验结果表明：模块化Grey-GMDH预测模型相对于传统的调和分析预测模型的预测精度均有显著的提高，且仿真实验结果同时验证了模块化Grey-GMDH预测模型的泛化能力和适用性。

5 结语

本文提出了一种基于灰色的数据处理群模块化(Grey-GMDH)潮汐水位实时预测模型。根据潮汐的产生原因，模块化将潮汐分解为两部分：天文潮部分和非天文潮部分。使用Grey-GMDH模型和调和分析模型分别对潮汐的非天文潮和天文潮部分进行仿真预测，对于非天文潮部分使用灰色模型进行数据预处理以减轻非线性影响因素，最后将两部分的预测结果综合形成最终的潮汐预测值。仿真实验结果证实了该方法的可行性与有效性并取得了良好的效果，具有较高的预报精度。但是随着预报时间的增加延长，本模型的预测精度会有一定程度的下降，因此使用本模型进行长期潮汐水位预报，并提高长期潮汐预测的精度将是作者接下来的主要研究工作。