一种扁薄副翼全电舵机动态响应的仿真计算*

杜永刚， 付朝晖，谭 立，刘轶鑫，杨震春

(兰州空间技术物理研究所, 甘肃 兰州 730000)

引 言

舵机系统是控制飞行器飞行姿态和航迹的系统，而舵机机构是操纵舵面偏转的执行机构，在无人机、导弹上等都有广泛的应用。早期的舵机大部分采用大功质比的液压和气动器件，此类舵机的缺点是结构复杂，体积大[1-3]。由于电动舵机具有体积小、易于维护、经济性及动态特性好等特点[4]，因此近年来，世界各国在导弹舵机中都趋于使用电动舵机[5]。随着现代制导武器高机动性能要求的提高，现代某些导弹也利用副翼进行姿态调整[6]，但是超薄的翼型内部无法安装机构，往往导致设计搁浅[7]。可以预见，小型化的电动副翼舵机也是将来的发展趋势之一。根据资料显示，目前副翼舵机采用铰链传动机构，这种传动机构的铰链部位会超出翼的外形，突出部位对导弹的气动和隐身产生很大的影响。针对该技术问题，研究人员设计了一种厚度不超过35 mm的扁薄电动副翼舵机，并以带宽大于10 Hz、负载能力不小于20 N·m为目标，对这种扁薄电动副翼舵机的可行性进行了研究。

1 舵机的性能及其传动机构

目前，国内的电动副翼舵机机构大多采用铰链连杆传动机构，比如文献[8]中利用高精度控制电机直接拖动丝杆螺母获得直线运动，进而由螺母移动和连杆机构的结合来实现电机和翼面之间的运动传递，其缺点是连杆会凸出副翼的外形，且在连杆的运动极限位置传动效率会降低。本文在这种机构的基础上进行了改进设计，舵机机构仍采用电机驱动丝杆螺母，获得直线运动后，由螺母的运动和拨杆机构的结合，解决了机构凸出翼面和极限位置效率降低的问题。整机外形见图1，其机构原理见图2。机构由一个滑动副S1、2个高副G1和G2及2个低副J1和J2组成，图2中的F0是丝杆输出力，O1和O2是旋转轴，A和B都是机构连接点。舵机的设计目标：铰链力矩≤ 20 N·m，翼面偏转角度为±20°，系统带宽不小于10 Hz，输出转角单位阶跃响应的上升时间τT≤0.1 s，稳态误差es≤1%，超调量σ≤10%，扰动单位阶跃信号的响应峰值γmax≤0.4°，稳态值γss≤0.1°。

图1 副翼舵机外形

图2 机构原理图

舵机系统的带宽、效率等也是主要的设计考虑因素[9-10]，所以除了考虑紧凑、扁平形式传动机构的布局设计外，也要求系统的带宽不小于10 Hz，并具备优良的位置跟踪精度和速度。因此，经过计算舵机系统的减速比为449∶1，采用两级传动方式，第一级用与电机串联的行星齿轮减速箱，传动比为23∶1；第二级在工作点0°的减速比为19.5∶1。设计中考虑了消除机械传动间隙，防止舵机在频繁换向时引起的系统震荡[11-12]，本文设计的副翼舵机的传动部件是高精度的滚珠丝杆，设计螺母和拨杆的配合最大间隙为0.01 mm，可忽略。电机齿轮箱空回约为1°，换算到输出轴约为(1/449)°，也可忽略。此外，所有传动轴尽量安装预紧滚动轴承，尽量消除旋转运动的间隙。采用这些消除运动间隙的措施后，配合间隙对系统的影响可以忽略不计，为了简化计算，在理论仿真计算中也不再考虑机构间隙的影响。

2 电动舵机模型的建立

2.1 电机和机构组合体的数学模型

对于设计的2通道电动舵机，只需建立单通道舵机的模型就能表征整个系统。为了简化起见，对舵机机构的非线性传动环节进行必要的线性处理，将机构的质量特性折算到电机轴和负载上。

电机输出扭矩：

To(s)=TL(s)-Td(s)

式中：TL是负载扭矩；Td是扰动力矩；s是复变因子。

电机轴上的负载扭矩由电机轴上的惯性负载和副翼通过减速机构传递到电机轴上的负载，即：

TL(s)=Js2θ(s)+bsθ(s)+To(s)

式中：θ为电机轴的转动角；To为电机轴输出的扭矩；J为转动惯量，J=Jm+Js/i，其中Jm为电机转子转动惯量，Js为传动机构等效的转动惯量，i为电机齿轮箱减速比；b为阻尼力矩系数。

在扰动Td=0的情况下，电机转子的动力学方程为：

(1)

式中：τL为转子时间常数，τL=J/b；I(s)是励磁电流；Km为电机常数；θm为电机轴旋转角度。

对于减速机构部分，由机构原理可以看出，其输出和输入关系为非线性关系，需要在其动态考察点进行线性化处理。如图2所示，拨杆的转轴圆心为O1，拨杆可以绕O1转动，舵面转轴为O2，机构连接点为A，舵面连接点为B，其运动轨迹方程为：

(2)

式中：L2为舵面上B点与舵面转轴之间的臂长；θw为副翼转角；(x2,y2)为B点坐标；(a,b)为O2点坐标；R为B点绕O1点的旋转半径。

按照表1中的机构参数进行了线性一次拟合，得到线性修正系数κ=1.099 3，所以有：

式中：H0为拨杆臂长度；d2为螺杆工程中径；γ为螺杆升角。

根据表1中的参数得到θm=449θw。由机构原理图可以得出：

式中：ρ′为当量摩擦角；Tload为作用在副翼上的力矩。

根据表1中的参数，可以得到To=0.001 86Tload。实际的铰链力矩是弹性载荷，因此在θw=±2°的偏转角范围内，Tload和θw成正比关系，所以有副翼载荷Tw=KLθw，其中KL=1 N·m/(°)，可推得To=0.001 8θw。综合以上分析，可以得到电机和机构组合体的动力学方程：

(3)

表1 机构参数

2.2 控制器的数学模型

20世纪50～60年代以来，PID控制器在飞航导弹控制系统中应用得十分普遍和成功，它具有直观、实现简单、物理意义明确、调整方便和鲁棒性好等优点。即使在当代，型号产品的成熟性和继承性依然是重点考虑的因素，所以该舵机系统要求采用成熟的PID控制算法。本文的舵机控制器采用串级控制，分为位置环(APR)、速度环(ASR)和电流环(ACR)，这样可以保证系统的稳定性和响应速度。ACR使控制器产生足够的快速电流以加速负载惯性，所以采用了比例控制环节。ASR系统获得快速跟踪的能力，采用PI环节，而没有引入微分环节，防止产生过大的超调。APR是位置环，铰链力矩的大范围变化会引起稳态误差，为了达到理论上的零稳态误差，位置环采用了PID控制。通过对三环参数的优化使舵机系统的位置控制精度、响应带宽达到实际的设计要求。

3 舵机系统的仿真分析

通过Matlab/Simulink工具对舵机系统的动态仿真模型进行计算(如图3所示)，验证电动舵机在弹性负载情况下对阶跃输入信号、正弦输入信号的响应特性，对设计的舵机系统的快速性、系统带宽、对位置指令的跟踪性能进行仿真计算。仿真中采用的舵机机构的参数见表2。

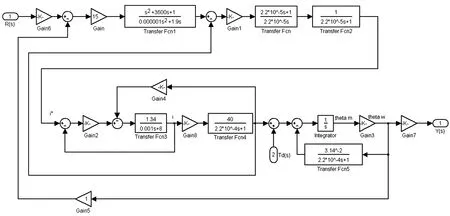
图3 Simulink建立的舵机系统仿真

KmR/ΩL/mHJ/(kg·m-2)bτLi0.14811.1×10-50.052.2×10-41/449

在单位阶跃输入信号下，仿真舵机系统的快速性。图4是副翼电动舵机在单位阶跃输入信号下的响应曲线，上升时间为93.86 ms，超调量为0。表3列出了舵偏角分别为5°、10°、15°和20°阶跃响应时对应的上升时间、超调量以及稳态误差。从仿真结果可以看出，仿真的阶跃响应曲线的上升时间τT最大为104.5 ms，超调量σ=0，稳态误差es=0。

图4 单位阶跃响应曲线

τT/ms 2°5°10°20°σes808893.87104.500

系统动态性能测试通常是通过正弦信号判断出舵机系统对正弦位置指令的跟踪能力，图5是在输入正弦测试信号的频率为10 Hz、舵偏转角幅值为2°下的仿真结果。图6是舵机系统的幅频特性仿真曲线。由仿真结果可以看出，舵机偏转角在2°时，其带宽约为10 Hz，在图6的10 Hz频率点，系统增益下降至0.82，相位偏转约为-45°，达到系统要求下限。

图5 2°@10 Hz下的正弦信号的响应

图6 幅频特性和相频特性曲线

本文也进行了力矩干扰抑制的仿真，实际的测试干扰是突然加载一个扰动力矩，在仿真计算中，利用单位阶跃信号模拟扰动力矩。图7是在扰动单位阶跃输入信号下的响应仿真曲线，输出干扰转角单位阶跃响应的峰值γmax=0.002°，稳态值γss=0.002°，满足系统指标要求。

图7 扰动单位阶跃响应曲线

4 结束语

本文主要根据某超薄翼型用舵机的需求，设计了一种扁薄副翼全电舵机机构，建立了电机和机构组合体的数学模型，采用串级PID控制器进行了仿真。仿真结果表明，设计的副翼全电舵机系统在测量舵偏角±2°时，带宽达到10 Hz，单位阶跃响应上升时间τT≤0.1 s，稳态误差es=0，扰动单位阶跃信号的响应峰值γmax≤0.4°，稳态值γss≤0.1°，在扁薄体积下，具有高速、高精度、较好的动态特性的优点，可用于超薄翼型的全电舵机的设计参考。