Frequency-domain Response Analysis of Adjacent Multiple Floaters with Flexible Connections

CHEN Ming-sheng,ZOU Mei-yan,ZHU Ling

(1.Key Laboratory of High Performance Ship Technology of Ministry of Education(Wuhan University of Technology),Wuhan 430063,China;2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration(CISSE),Shanghai 200240,China;3.School of Transportation,Wuhan University of Technology,Wuhan 430063,China)

Abstract:Many offshore operations may involve two or more floaters operating in close proximity,such as the catamaran float-over deck installation for offshore platforms.The adjacent floating structures would experience hydrodynamic interactions under wave excitations.In addition,gap resonances may be induced under certain specific conditions and the resulting large wave forces may cause structural damage to the floaters.The adjacent floaters may be linked with flexible connectors.For this case,it is necessary to consider the coupled effects of hydrodynamic interactions and the constrained forces from the flexible connectors on the motions of the floaters as well as the effects of the constraint forces on the structural behaviour of the connectors.Hence,a coupled multi-body hydrodynamic-structural dynamic model needs to be established to investigate the dynamics of interconnected floaters under the complex environmental loads.Taking catamaran float-over deck installation as the research background,this paper develops a coupled hydrodynamic-structural model to analyze the complex dynamics arising from catamaran tow of the platform topsides.By combining dynamic substructuring and static condensation as well as considering the flexibility of connectors,the mass and stiffness of the connector are condensed to the connection points on the carrying barges.Based on the frequency-domain hydrodynamic analysis of the carrying barges,the dynamics of the barges is analyzed by considering the effects of both the multi-body hydrodynamic interactions and the constraint of the flexible connectors.

Key words:multi-body hydrodynamic interaction;catamaran tow;static condensation;dynamic substructuring;dynamic responses

0 Introduction

Many offshore operations may involve two or more floaters operating in close proximity,such as the catamaran float-over deck installation for offshore platforms.The catamaran floatover method is an old fashion as the single barge float-over method,and was developed in the late 1970s for installing heavy integrated decks for floating Gravity Based Structure(GBS)platforms in sheltered waters like fjords[1].For these installations,water was firstly pumped into the floating GBS to ballast it down to the seabed and the deck supported by two barges was then floated onto the GBS by either de-ballasting the GBS or concurrently de-ballasting the GBS and ballasting the two barges.Float-over operation in sheltered water puts less demand on the design of the mooring and shock-absorber devices since the deck installation is generally executed in calm waters[2].In addition,the towing of the deck supported by twin barges(catamaran tow)in open water may cause a challenge that the deck system would withstand numerous racking forces induced by the out of phase motions of the twin barges[2-3].The first open water catamaran float-over deck installation was carried out for the Kikeh SPAR platform that is also the first SPAR outside of the Gulf of Mexico(GOM)[4].This float-over operation involved single barge deck transportation phase(single barge hydrodynamics),catamaran tow phase(twin barges in close proximity)and in-place mating phase(SPAR hull in between the twin barges).The deck system was specially designed to withstand the extra structural loadings caused by the out of phase motions of the twin barges.

During catamaran tow and in-place mating stage,the multi-body hydrodynamic interactions need to be investigated carefully.In addition,the integrated deck system would experience numerous racking forces due to the out-of-phase motions of the twin barges.Due to the large span between the two barges,the flexibility of the deck may need to be investigated.Sun et al[5]analysed multi-body hydrodynamic interactions arising from the float-over deck installation onto a GBS platform.The hydrodynamic interactions between the float-over barge and GBS are found to be very significant and need to be simulated using the 3D hydrodynamic codes.Sun et al[6]investigated the wave-induced responses of the catamaran system during catamaran tow of a catamaran float-over deck installation.For this case,the integrated deck was modelled as a flexible structure that is condensed to a number of super nodes(DSU connections)attached onto the twin barges using the method of substructuring with static condensation.

This paper proposes an integrated hydrodynamic-structural analysis model that is applicable for analysing catamaran float-over deck installation,with emphasis on the modelling of catamaran tow in the frequency-domain.The complex hydrodynamic interaction between two barges in a catamaran configuration is investigated.A case study is conducted to validate the methodology using substructuring with static condensation.The case of two barges interconnected by two horizontal beams is analyzed to study the effects of flexible connectors on the dynamics of the two barges.This paper is arranged as follows.Chap.1 describes the methodology of the proposed study.Validation of the methodology using substructuring with static condensation is given in Chap.2.Chap.3 shows the hydrodynamic analysis of the twin barges and discusses the phenomenon of hydrodynamic interaction.Chap.4 introduces the analyses of the twin barges interconnected by two horizontal beams.Finally,some concluding marks are given in Chap.5.

1 Methodology

1.1 Frequency domain analysis in DIFFRACT

This study performs hydrodynamic analysis of the catamaran barges using the well proven 3D hydrodynamic codes DIFFRACT[7-8],from which the first-order wave excitation forces and hydrodynamic coefficients can be obtained.The frequency-domain Response Amplitude Operators(RAOs)of multiple floating structures at the freely floating condition can be derived from the following equation:

where Mbb∈（6N）×（6N）is the rigid body mass matrix and Cbb∈（6N）×（6N）is the hydrodynamic restoring matrix[9];N is the number of bodies in hydrodynamic analysis(N=2 for catamaran tow and N=3 for in-place mating stage);）∈（6N）×1 is the wave excitation force vector;AH（ω）∈（6N）×（6N）is the frequency dependent added mass matrix;BH（ω）∈（6N）×（6N）is the frequency-dependent added damping matrix;Bv∈（6N）×（6N）denotes the linear viscous damping matrix and）∈（6N）×1 gives the amplitude and phase of motion due to the wave excitations.

1.2 Substructuring with static condensation for modelling the twin barges with flexible connections

In this paper,the two-stage method proposed by Sun et al[6,10]is applied to analyse the hydrodynamic and mechanical interactions between two flexibly connected rigid barges.Following this methodology,an integrated hydrodynamic-structural analysis method can be developed to analyse the complex interactions between the twin barges during the catamaran tow.A typical example of the two barges with flexible connections is shown in Fig.1.The flexible substructure can be either the flexible deck or horizontal braces used to reduce the relative motions between the twin barges during the catamaran tow.As illustrated in Fig.1,the motions of the barges are designated as Xb;the motions at the connecting points between the flexible deck and the twin barges are selected as the master degrees of freedom Xmof the substructure;and the other nodal motions are chosen as slave degrees of freedom Xs.Hydrodynamic analysis is firstly conducted based on the chosen barge models,to calculate the wave excitation forces and hydrodynamic coefficients.Using substructuring with static condensation,the flexible substructure can be condensed to the master degrees of freedom using a typical FEM structural analysis solver.With the condensed mass and stiffness matrices of the flexible substructure,the wave-induced dynamics of the twin barges can be easily evaluated.

Fig.1 Two rigid barges with flexible substructure

By assuming that the only external forces acting on the substructure are the constraint forces）induced at the master nodes,the dynamic equation of motion for the substructure can be expressed in the following partitioned form[6]:

where the subscripts m and s denote the master and slave degrees of freedom,respectively;and the superscript T denotes transpose.

The overall displacement and acceleration vectors of the substructure are shown below:

In Eq.(2),the structural damping terms are neglected since the resonant responses in the substructure itself will not be investigated.The second equation of Eq.(2)has the following form:

Using static condensation,the inertial forces can be neglected in Eq.(4)and the slave degrees of freedom Xscan be expressed in terms of the master degrees of freedom Xm:

where Tmsis the coordinate transformation matrix between the master and slave degrees of freedom,which is independent of time.

Thus,the acceleration vector of the slave degrees freedom can also be derived based on the master degrees of freedom:

Then,Eq.(3)can be rewritten as:

where I is the identity matrix and TGis the transpose matrix.

Substituting Eq.(7)into Eq.(2)and pre-multiplying Eq.(2)bylead to:

The above equation only involves the master degrees of freedom Xm（t）and the corresponding constraint forces Fm（t）.The condensed mass matrixand stiffness matrixat the master nodes are as follows:

Since the master nodes are always attached onto the rigid barges,an explicit relationship between the motions of the master nodes and the rigid barges exists:

where Tbmis the coordinate transformation matrix between the master nodal motions and the rigid barge motions,which is independent of time;Xb（）tis the degrees of freedom of the rigid barges.

Substituting Eq.(9)and Eq.(10)into Eq.(8),the following expression is obtained:

The above equation can be used to calculate the constraint forces acting on the substructure based on the rigid barge motions.The corresponding constraint forces acting on the barges can be derived as follows:

The total forces acting on the barges include hydrodynamic forces（t）consisting of both the wave diffraction and radiation forces,hydrostatic forces CbbXb（t）,viscous damping forces）and the constraint forces as shown in Eq.(12):

where the convolution term represents the wave radiation forces and K（t）is the matrix of retardation functions(impulse response functions);AH（∞）is the infinite-frequency added mass matrix;（t）is the time series of the wave excitation forces and for monochromatic waves it has the following form:

The equation of motion for the rigid barges can be written as:

The above equation establishes a time-domain model for analyzing any possible nonlinear effects arising in the catamaran float-over deck installation,in which the time-consuming convolution term can be replaced by a state-space model,resulting in an efficient constant pa-rameter time-domain model.It can be extended to analyse the multi-body impacts arising in the mating stage,as reported by Chen et al[11-12]and Zou et al[13].Considering monochromatic waves,Eq.(15)can be investigated in the frequency-domain to calculate the RAOs of rigid barges:

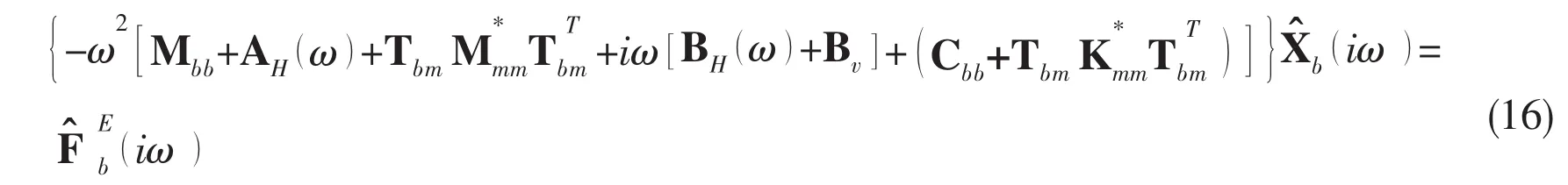
Based on the calculated rigid barge RAO and Eq.(11),the constraint forces acting on the substructure can be derived in the frequency-domain:

The RAOs of the master and slave degrees of freedom of the substructure can be derived as follows:

2 Validation of the methodology

This chapter describes the implementation of the integrated hydrodynamic-structural analysis method for analysing catamaran tow.The case of two barges with a beam connection analysed by Newman[14]and Sun et al[10]is analysed to verify the established methodology.Fig.2 shows the schematic of the two barges with a beam connection.The body mesh of the two barges used in DIFFRACT is shown in Fig.3.Fig.4 shows the beam model in the structural analysis solver by which the static condensation of the beam model is carried out to derive the condensed mass and stiffness matrices as defined in Eq.(9).These matrices are scaled to the values defined by Newman[14].The condensed stiffness represents rigid connections between the beam and the two barges.As shown in Fig.5,the heaving mo-tions of the two barges are simulated and validated with published results by both Newman[14]and Sun et al[10].It can be observed that the present results agree quite well with published results,which validates the accuracy of the present methodology.

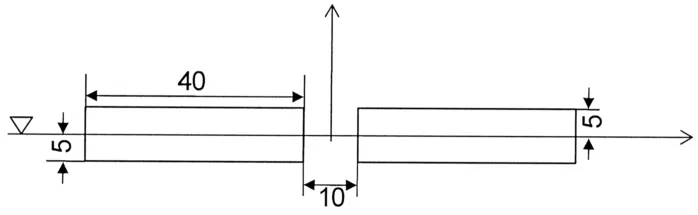
Fig.2 Schematic of the two barges with beam connection

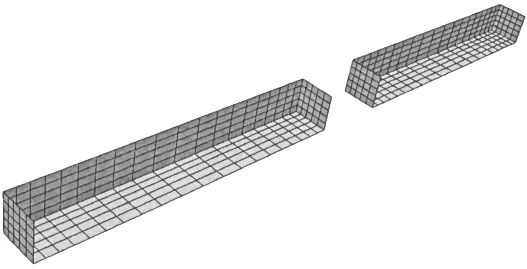
Fig.3 Body meshes of the two barge

Fig.4 Beam model in the FEM structural solver

Fig.5 Validation of the present methodology

3 Hydrodynamic analyses of twin barges in a catamaran tow

This chapter discusses the frequency-domain results for different configurations,including single barge,twin barges in close proximity during catamaran tow and catamaran barge by modelling the twin barges as one rigid body.These analyses aim to investigate the complex hydrodynamic interactions that one body’s presence has a significant effect on the hydrodynamic forces of the other adjacent body.

3.1 Model particulars

The twin barges analyzed in this paper are loosely based on the models described by Koo et al[15-16].Tab.1 summarizes the specifications of the barge models.The twin barges are symmetric along both x and y axes as shown in Fig.6.The gap between the twin barges is 41 m in the transverse direction.

Fig.6 Plan view of the twin barges in close proximity

Tab.1 Specifications of the barge models

Continue Tab.1

3.2 Frequency domain analysis of different scenarios

To investigate the effects of hydrodynamic interactions between multiple structures,three configurations are analysed in the frequency-domain:single barge,twin barges and catamaran barge.The single barge configuration represents single body hydrodynamics;the twin barges configuration models the catamaran tow stage with the twin barges in close proximity;the catamaran barge case is carried out to provide possible comparisons with the RAO test results reported by Koo et al[15].Due to the memory limit of the computer and to save computation time,one plane of symmetry is adopted in DIFFRACT as shown in Fig.7 and the coordinate system in DIFFRACT is different from the coordinate system defined in Fig.6.Thus,the calculated frequency-domain results from DIFFRACT will be converted to the coordinate system defined in Fig.6 to ensure that the translational motions in x,y and z axes are surge,sway and heave,respectively;and the rotational motions about x,y and z axes are roll,pitch and yaw,respectively.The water depth for all the analysed configurations is chosen as 347.8 m corresponding to the model test water depth as reported by Koo et al[15].

Fig.7 Body meshes in DIFFRACT(a:single barge;b:twin barges and catamaran barge)

Tab.2 Summaries of the frequency-domain analyses carried out in DIFFRACT

Fig.8 shows the comparisons of the diagonal terms of added mass coefficients of barge 1 for the configurations of single barge and twin barges.The added mass coefficients for the twin barges show first a maximum and then a minimum(sometimes negative)at the sloshing frequencies corresponding to standing waves between the barges.In addition,due to the multibody hydrodynamic interactions,the added mass coefficients of the barge 1 in the modes of sway to heave,heave to roll and pitch to yaw become nonzero.Fig.9 shows the comparisons of the diagonal terms of added damping coefficients of barge 1 for the configurations of single barge and twin barges.At the sloshing frequencies,the added damping coefficients exhibit delta function-like behaviour at the configuration of twin barges.Similar to the added mass coefficients,the added damping coefficients of the barge 1 in the modes of sway to heave,heave to roll and pitch to yaw become nonzero.In addition,it needs to be noted that the sloshing behaviour is restricted to a relatively narrow frequency band for both added mass and added damping coefficients.Besides,the sloshing behaviour is much less significant in the mode of surge but much more significant in the modes of sway and yaw.

Fig.8 Diagonal terms of added mass coefficients of barge 1 for different configurations

The sloshing frequencies can be identified by plotting the hydrodynamic coefficients versus the gap-to-wavelength ratio as defined[17]:

where d=41 m is the gap between the twin barges and λnis the wavelength associated with nth mode of sloshing.

The nth mode of sloshing frequency can be calculated based on dispersion relation:

where g is the gravity acceleration and w is the water depth.

Fig.9 Diagonal terms of added damping coefficients of barge 1 for different configurations

Fig.10 Hydrodynamic coefficients versus gap-to-wavelength ratio of barge 1 in the modes of yaw to yaw

The above equation is only good for ‘deep water’ while the present calculation considers 347.8 m water depth.Fig.10 shows the yaw to yaw added mass coefficients and added damping coefficients of barge 1 versus the gap-to-wavelength ratio,respectively.Different orders of sloshing modes are clearly identified.For this mode of motion,significant sloshing behaviour is even observed up to the 7th mode of sloshing.

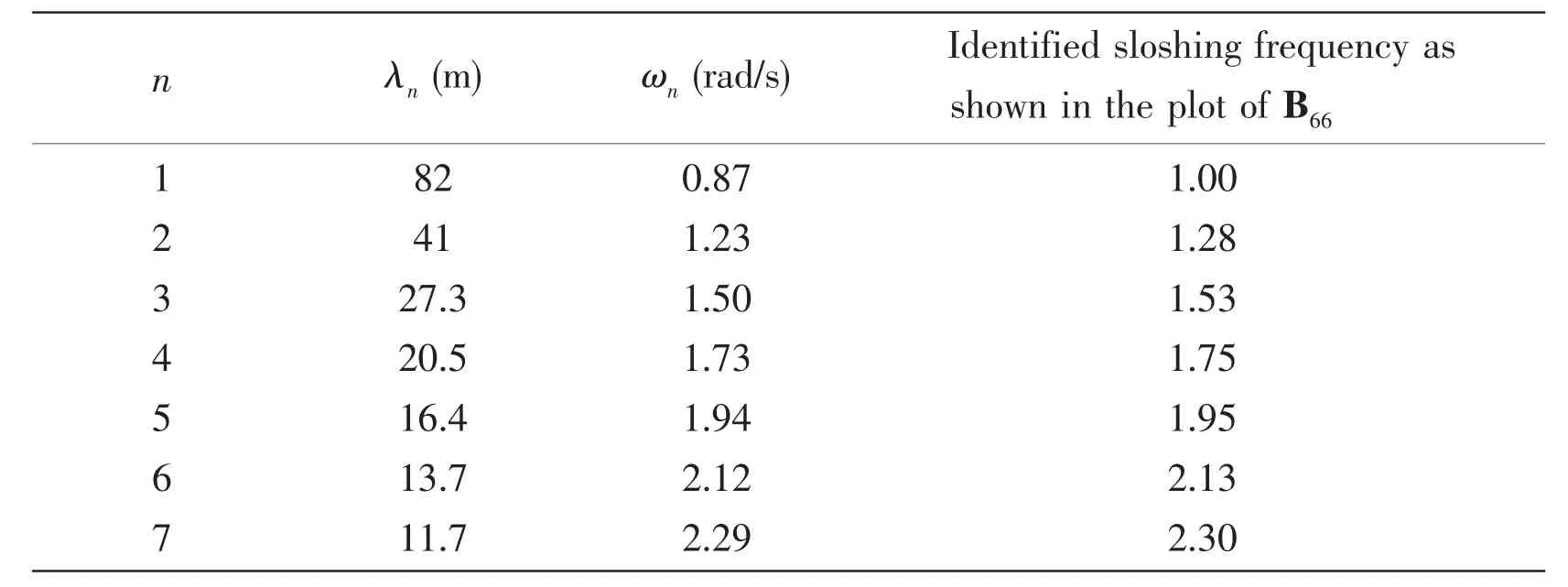
Tab.3 summarizes the calculated sloshing frequencies via Eq.(20)and identified sloshing frequencies based on the plot of B66as shown in Fig.10.There are significant discrepancies between the calculated and identified sloshing frequencies for the lower sloshing modes where the corresponding wave length λnis relatively large and cannot be considered as ‘deep water’for the 347.8 m water depth.That is to say,the finite water depth results in a shift of the lower sloshing modes compared to the case of infinite water depth.As n increases,the wavelength decreases and thus the discrepancies between the calculated and identified sloshing frequencies become insignificant for the higher sloshing modes due to the fact that the condition of‘deep water’ is satisfied.In practice,the wave periods generally range from 4 s to 18 s.Hence,only the identified lower sloshing modes are of importance to the evaluation of the hydrodynamic characteristics of these multi-body systems.Although the sloshing frequencies can be approximated,the exact magnitude of the hydrodynamic coefficients at these frequencies can hardly be obtained as these values strongly depend on how close the calculation frequency is to the actual sloshing frequency[17].

Tab.3 Comparison of the calculated and identified sloshing frequencies

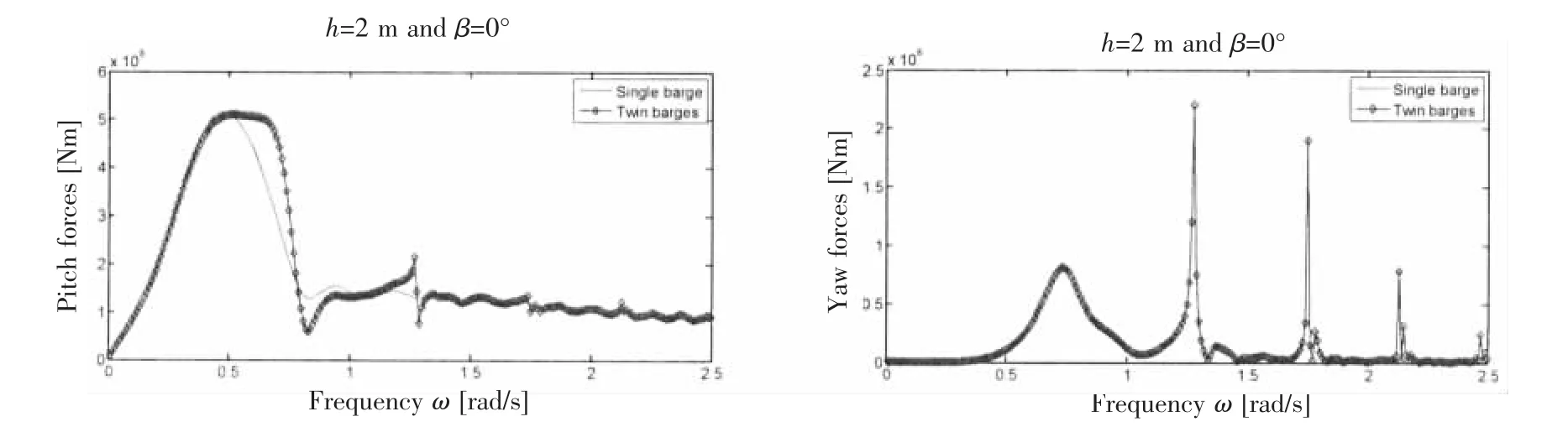
Fig.11 Wave excitation forces acting on the barge 1 under the head sea-state for different configurations

Fig.11 plots the amplitudes of wave forces acting on the barge 1 under the head seastate.Significant differences of the wave forces are observed for different configurations.Specifically,large increase or drastic change of wave forces is observed at these sloshing frequencies.In addition,due to the presence of the barge 2,the wave forces acting on the barge 1 in the modes of sway,roll and yaw are nonzero,which is different from the single barge case.

Fig.12 Comparison of RAOs of barge 1 for different configurations under the head sea-state

Figs.12-14 plot the RAO comparisons for different configurations under the head seastate,beam sea-state and quartering sea-state,respectively.Under the head sea-state,the model test results of heave and pitch RAOs are also compared with the numerical results.The configuration of catamaran barge models the twin barges as one rigid body,corresponding to the catamaran tow phase.The RAO results of the catamaran barge match well with the model test results.For the beam sea-state,the RAO results of the catamaran barge also match well with the model test results in the modes of heave and roll.For the quartering sea-state,the RAO results of the catamaran barge match well with the model test results in the modes of heave,roll and pitch.Generally,different configurations experience different motion characteristics.In addition,the configuration of twin barges experiences more complex oscillations in the RAO plots compared with the configurations of single barge and catamaran barge.

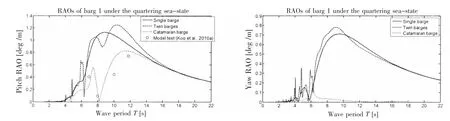
Fig.14 Comparison of RAOs of barge 1 for different configurations under the quartering sea-state

4 Twin barges interconnected by two horizontal beams under the beam sea-state

This chapter considers a more complex case arising in catamaran tow that the twin barges are interconnected by two horizontal beams to reduce the out of phase motions between the twin barges.Fig.15 demonstrates the configuration of twin barges constrained by two horizontal beams.Each beam is modelled as two Euler-Bernoulli beam elements.The axial stiffness EA of the beam element is chosen as 1.0E+15 N/m and the bending stiffness EI is 1.0E+20 Nm2.The length of each beam element is a=20.5 m,which is half of the gap between the twin barges.The mass per unit length of the beam is taken to be 10 kg/m.In the common joint of each horizontal beam,a rotational spring with stiffness of C is modelled,with C=0 corresponding to a hinged connection and C=1.0E+12 Nm/rad corresponding to a rigid connection.

Fig.15 Configuration of the twin barges interconnected by two horizontal beams

Fig.16 compares the RAOs of the twin barges with rigid or hinged connections at the midsection of the horizontal beams.For the rigid connection,the twin barges move like one body,having the same motion amplitudes.In addition,the heave RAOs match well with the model test results.For a hinged connection,the twin barges show different motion characteristics but still have the same sway motions.Compared to the rigid connection,the hinged connection results in that the barge 1 experiences much larger roll amplitudes.Fig.17 shows the comparison of the twin barges for different bending stiffness of the horizontal beam with hinged connection at its midsection.Compared to the freely floating condition,adding the two horizontal beams would help to reduce the sway and heave motions.In addition,the two beams with rigid connection are found to significantly reduce the roll motions of the twin barges.Larger bending stiffness is found to reduce the heave motions of the barges for the normal wave periods range considered.

Fig.16 RAOs of the twin barges with hinged connections at the midsection of the horizontal beams(1st column:rigid connection;2nd column:hinged connection)

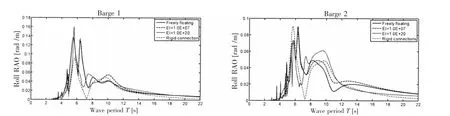
Fig.17 Comparison of RAOs of the twin barges for different bending stiffness of the horizontal beams

5 Concluding remarks

This paper gives a brief description of the proposed integrated hydrodynamic-structural analysis method for analysing catamaran tow.By condensing the mass and stiffness of flexible connectors onto the connection points on the rigid barges using substructuring with static condensation,the dynamics of two barges with flexible constraints can be readily obtained.The accuracy of this method is validated with published results by considering two boxes with a hinged connection and good agreement is achieved.The strong hydrodynamic interactions arising in the configurations of twin barges in close proximity are investigated by analysing the different sloshing modes of the waters between the two barges.A case study of twin barges interconnected with two horizontal beams is carried out to demonstrate the implementation of this method for analysing catamaran tow.It is found that adding horizontal beams help to reduce the motions of the twin barges,which may be useful to enhancing the safety of the deck transportation using two barges for a catamaran float-over deck installation and other offshore operations involving interconnected multiple floaters.The proposed methodology can also be further applied to calculate the constraint forces at the connection points,which would have implication on the design of flexible connectors and thus need to be explored in future studies.