Investigation on Higher-Order Responses of Vortex-Induced Vibration for a Mounted Cylinder

WANG Ren-feng,CHEN Ke,YOU Yun-xiang,DUAN Jin-long

(1.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration,Shanghai 200240,China)

Abstract:According to its significant effect on the structural vortex-induced vibration(VIV),higher-order responses of VIV on a mounted cylinder in a uniform flow is investigated on the basis of the classical Van der Pol wake oscillator.Both the first-order and higher-order responses are discussed for the interaction of a wake oscillator and a linear spring-mass-damper system.Equations are established to model the mechanism of VIV concerning the first-plus higher-order responses,and the analysis of the dynamical performance includes displacement,velocity and acceleration coupling terms.Moreover,comparison with the motion characteristics that only take the first-order response into account is made for various mass damping ratios.The results show that the new model based on the first-plus higher-order responses can characterize the behavior of VIV more precisely,such as the amplitudes of structural vibrations.The motion amplitudes of the wake oscillator and the cylinder enlarge to certain degrees,respectively.Although features of the higher-order responses including structural motion amplitude are several orders of magnitude smaller than that of the first-order response,it is not negligible according to its apparent influence on the first-order response.

Key words:vortex-induced vibration(VIV);structure and wake oscillator coupling;Van der Pol oscillator;first-plus higher-order responses

0 Introduction

Because of its dramatic influence on ocean structures,vortex-induced vibration(VIV)has been investigated over the past several decades.When VIV occurs,complicated and drastic interactions between the fluid and the structure will be triggered.Specifically,when a cylin drical structure encounters VIV,as a result of the instability of fluid,boundary layer will separate from the structure at a certain velocity.Meanwhile,the periodic force generated by the fluid makes the structural vibration,and the motion of the structure influences the characteristics of the fluid simultaneously.Additionally,the vortex shedding frequency locked into the structural natural frequency leads the amplitudes of the structural motions into drastic increase until the peak value appears at lock-in[1].Consequently,potential fatigue damage is possibly involved in deep-sea exploration and production when VIV occurs.

Numerous fundamental studies on VIV have been reported,and there are three major methods of the research on VIV:experimental method,semi-empirical method and computational fluid dynamics(CFD)method[2-3].As the most direct approach,experimental method can reproduce actual conditions.It focuses on structural motions,fluid forces and mode transition of VIV at different mass damping ratios[4-6].However,in some cases,experimental method is hardly available due to the restriction of experimental conditions.Although CFD method can reasonably simulate the hydrodynamic forces that act on a tensioned riser[7-8],it is difficult to be fully implemented in industrial design because of the insufficient understanding of turbulence.Especially,as a result of time-consuming,CFD method is barely practical for large aspect ratio risers.Semi-empirical models,on the contrary,are more feasible and efficient to calculate the hydrodynamic forces initiated by vortices[9-11].

The original concept-Van der Pol equation-has been extensively discussed and utilized as an effective model[12-14].It is not only adopted to simulate the 3-D features of vortexes that shed off from stationary structures[15-16],but is also used to model VIV of slender structures in uniform and shear flows[17-19].Meanwhile,the forcing term,which is proportional to the displacement,velocity or acceleration in the Van der Pol equation,reflects the influence of structural motions on the wake[20].Modal analysis method has been widely utilized to investigate the characteristics of VIV[21-22].It shows that there are commonly multiple modes of response accompanying with VIV,and the effect of higher-order responses has been verified in a large number of studies[23-27].It is also worthwhile to note that peaks in the vibration spectrum mainly appear at the vortex shedding frequency(ω0)and its odd multiple harmonics(3ω0,5ω0,etc.),not at its even multiple harmonics(2ω0,4ω0,etc.).However,the solutions of structure and wake oscillator coupling vibration models have rarely concerned higher-order responses.

Therefore,in order to distinguish from the models that only the first-order response is considered,a higher-order response(first-plus higher-order responses)is involved in coupled structure and wake oscillator models.Only one higher-order response is selected to avoid the model being complicated.As for wake oscillator,it is simulated with the effective Van der Pol equation.Specifically,a structural vibration model is combined with the Van der Pol equation to model the transverse VIV of a cylinder in a uniform flow,and the dynamic behaviors in different modes of coupling are discussed.Moreover,the results that include the first-plus higher-order responses are compared with that only the first-order response is included.It shows that the characteristics of VIV are obviously effected by the higher-order response,such as vibration amplitudes and lock-in behavior.The influence of the mass damping ratio on motion amplitudes is also considered.

1 Physical and numerical model

1.1 Coupling model

As is shown in Fig.1,the elastically supported rigid cylinder with a diameter D vibrates transversely in a uniform flow,and the velocity of flow is U.The relation of the dimensional in-plane crossflow displacement Y and force S is shown as follow[1]:

where,overdot means the derivative with respect to time t.S=0.5 ρU2DCLindicates the influence of vortices on the structure,and CLis the lift coefficient.is structural angular frequency.ξ=3.1×10-3is structural reduced damping.r=rs+rfis viscous dissipation in the linear damping.rsis viscous dissipation in the support and rf=γρ ΩfD2is viscous dissipation in the fluid-added damping.is the fluid added-damping coefficient.CDis the drag coefficient,and CD=2.0 is determined to simplified the calculation according to Ref.[20].,and ρ is the density of fluid.S(Stt≈0.2)is the Strouhal number.is vortex shedding angular frequency.The mass m consists of two parts.One is the mass of structure ms,and the other is the fluid-added mass mfwhere CMstands for the added mass coefficient.

Fig.1 Model of coupled structure and wake oscillator for 2-D vortex-induced vibrations

The fluctuating nature of the vortex street is described with Van der Pol equation[28]

where ε=0.3[20],and F reflects the influence of structure on the near wake.

In order to couple the structural vibration equation and the wake oscillator equation,E-qs.(1)and(2)are written in a non-dimensional form:

where,overdot indicates the derivative with respect to non-dimensional timeandis the reduced angular frequency of structure,andis the non-dimensional form of U.s=Mq represents the effect of fluid on the structure.M denotes the mass number and M=2×10-4is determined.

Coupling interface f is defined on the basis of experimental values,that is,12y,andfor displacement,velocity and acceleration couplings,respectively.

1.2 Higher-order responses

Higher-order responses are mostly the odd multiple harmonics of the vortex shedding frequency.Thus,3ω (ω is time-independent first-order angular frequency)is chosen here to represent the higher-order angular frequency.No other higher-order responses are considered so as to simplify the equations and to clarify the computed results.The solution associated with the first-plus higher-order responses are as follows:

where q0and y0are amplitudes corresponding to the first-order response,while,q1and y1are amplitudes corresponding to the higher-order response.φ0,φ1and θ are relative phases.

Substituting Eqs.(5)and(6)into the structural vibration equation Eq.(3),then

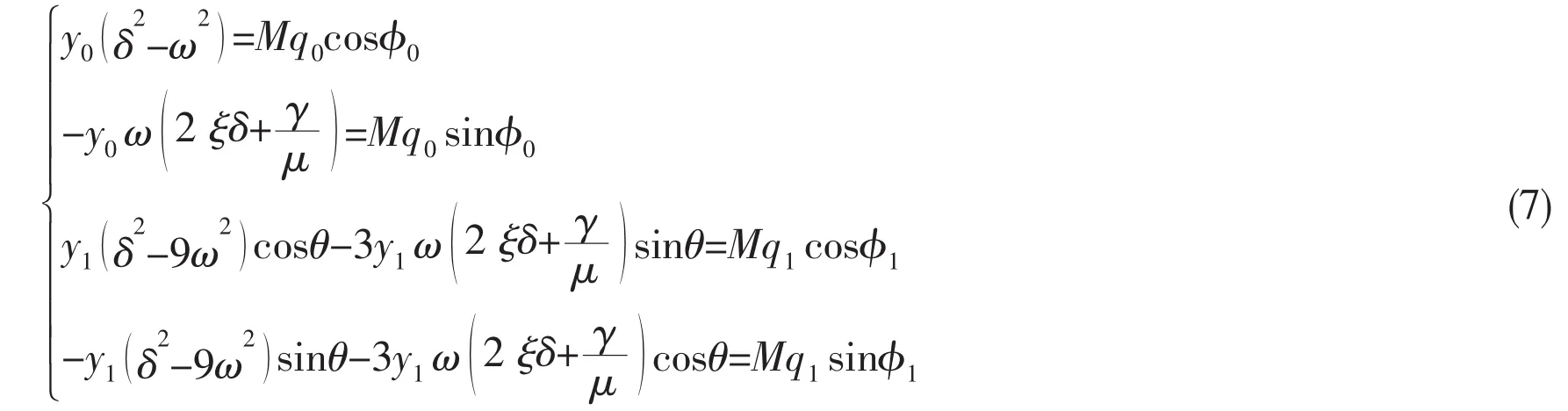
Substituting Eqs.(5)and(6)into the wake oscillator equation Eq.(4),then

As is shown in Tab.1,the coupling parameters C1,C2,C3and C4depend on the mode of coupling.

Tab.1 Coupling parameters C1-C4for different coupling modes

Continue Tab.1

Combining Eq.(7)and Eq.(8),the structure and wake oscillator coupling model is shown as follow:

where the coupling parameters G1-G6are shown in Tab.2.

Tab.2 Coupling parameters G1-G6for different coupling modes

2 Results and discussion

2.1 Amplitudes of the structural vibration

The amplitudes of structural motions that consider only the first-order response y0(Fig.2a),that consider the first-plus higher-order responses y(Fig.2a)and that consider only the higher-order response y1(Fig.2b)are shown in Fig.2.In all the three couplings,the amplitude of structural motions amplifies in the situation of lock-in,while the structure is nearly static during lock-out(y≪1).The higher-order response leads into new maximum values of the amplitudes in velocity and acceleration couplings.In acceleration coupling,the Urat which the peak value appears varies from 5 to 5.25 as ω decreases.And a small shift of the lock-in range also occurs for acceleration coupling,which is similar to the situation of q.However,there is no obvious distinction in the displacement coupling,even at lock-in.For y1,the variations of the amplitude occur at the same Uras the situation of q1(Fig.3b).The amplitude of the higher-order response is four orders of magnitude smaller than that of the first-order response.Although the higher-order response is not significant,it does play a major role in the effect of y.

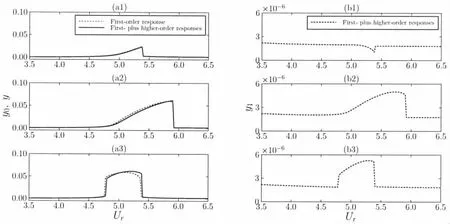
Fig.2 Variations of the amplitude of the structural vibration y0(a:—only the first-order response),y(a:—the first-plus higher-order responses)and y1(b:only the higher-order response)for different coupling modes as the reduced velocity Urincreases.(a1/b1:displacement model;a2/b2:velocity model;a3/b3:acceleration model.)

2.2 Motion amplitudes of the wake oscillator

Generally,the change regulation of q(Fig.3a)for the first-plus higher-order responsesrelated coupling and for the higher-order response-related coupling q1(Fig.3b)are similar to the situation that only the first-order response is concerned q0(Fig.3a).q1is significantly smaller than q0and q.However,the higher-order response results in a symbolic amplification of q at lock-in for velocity and acceleration couplings.The Urwhere maximum amplitudes appear is larger in the velocity and acceleration couplings that the first-plus higher-order responses are considered.Moreover,a slight shift of the lock-in range occurs in the acceleration coupling.

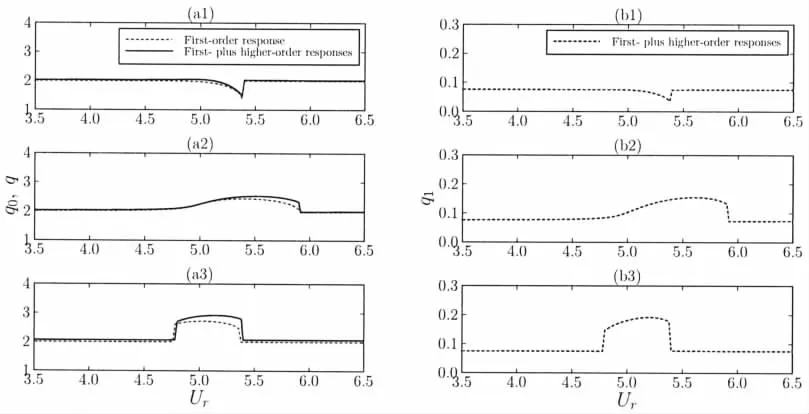
Fig.3 Variations of the motion amplitude of the wake oscillator q0(a:—only the first-order response),q(a:—the first-plus higher-order responses)and q1(b:only the higher-order response)for different coupling modes as the reduced velocity Urincreases.(a1/b1:displacement model;a2/b2:velocity model;a3/b3:acceleration model)

Fig.4 Amplitudes of structural vibrations yM at lock-in for different modes of coupling:…displacement coupling;---velocity coupling;-acceleration coupling.Blue,considering only the first-order response;Red,considering the firstplus higher-order responses.Experimental data:○Balasubramanian and Skop(1997,in air);□Balasubramanian and Skop(1997,in water);◇Khalak and Williamson(1999,in water)

2.3 Amplitudes of the structural vibration at lock-in

The maximum amplitude of structural motion at lock-in is commonly represented with Skop-Griffin parameterFor displacement and acceleration couplings,the reference resonance state is defined by ω= δ=1 andThe condition is ω= δ≠1 for velocity coupling[20].Consequently,as is shown in Fig.4,the motion amplitudes in different modes of coupling at lockin can be depicted in a Griffin plot.The maximum amplitudes of structural vibrations at lock-in for velocity coupling and acceleration couplings are slightly closer to the experimental results by considering the first-plus higher-order responses than by considering only the first-order response.That is,the effect of the higher-order response partly raises the accuracy of calculation.On the other hand,probably because of the small-scale amplitude,the structural vibrations in displacement coupling during lock-in are irrelevant to the higher-order response.

2.4 Influence of the mass damping ratio on motion amplitudes

The amplitudes of the wake oscillator q(Fig.5a)and the structural amplitude y(Fig.5b)at various values of mass damping ratio m*ξ(m*is mass ratio,)are depicted in Fig.5.They are significantly larger during lock-in considering the first-plus higher-order responses than that only considering the first-order response,especially for a smaller m*ξ.As is specifically shown in Tab.3,q and y at m*ξ=0.010 8 enlarge by 11.48%and 7.93%,respectively.The increase of q and y at larger values of m*ξ are not significant,which indicates that the influence of the higher-order response expands as m*ξ decreases.

Tab.3 Variations of q and y for different values of m*ξ

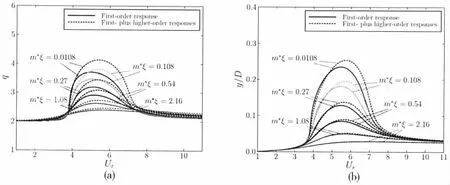
Fig.5 Variations of the motion amplitudes of the wake oscillator q(a)and of the cylinder y(b)at different values of mass damping ratio m*ξ as the reduced velocity Urincreases

Fig.6 Variations of the motion amplitude of the wake oscillator q1(a)and of the cylinder y1(b)at different values of mass damping ratio m*ξ as the reduced velocity Urincreases

Fig.6 illustrates the motion amplitudes of the wake oscillator q1(Fig.6a)and of the cylinder y1(Fig.6b)at various values of m*ξ.Because the dominant influence of the first-order response on the higher-order response,whether consider the higher-order response or not does not change the variation regularities of q1and y1.However,q1is one order of magnitudes smaller than q during lock-in and nearly two order of magnitude smaller out of lock-in.The significant increase of q1does not occur at Ur=1.7,but occurs at Ur=5.7 because of the interaction between the first-order and the higher-order responses.The amplitude of y1around Ur=1.7 is approximately twice larger than that at Ur=5.7.The huge enlargement of y1possibly leads into the growth of y.Moreover,y1increases as m*ξ decreases.

3 Conclusions

In addition to the first-order response,a higher-order response is observed with different structure and wake oscillator coupling models to validate the influence of higher-order responses on the characteristics of VIV.By considering the first-plus higher-order responses,more accurate results can be obtained,including lock-in range and maximum amplitude of vibration.Another important distinction between different modes of coupling is that acceleration coupling is better at computing the amplitude and lock-in range than displacement and velocity couplings.Moreover,comparison of the behaviors of VIV such as structural amplitude and Griffin plot are made between the model that only the first-order response is considered and the model with the first-plus higher-order responses.It shows that the latter is more available for a wide range of mass damping ratios,especially for a low mass damping ratio.On the other hand,computed results are closer to experimental data according to the amplitudes of structural vibrations shown in the Griffin plot,which confirms the effect of higher-order responses.

Therefore,it is a proper way to calculate the behavior of VIV with wake oscillator model that the first-plus higher-order responses are considered.And high-order responses are indispensable in the prediction of structure fatigue damage.However,the error of the computed values is still relatively excessive,which needs to be solved in further investigation.