椭圆榫节点抗弯强度的数值分析研究

胡文刚，关惠元

榫卯结构因精巧的外观、牢固的结构而著称，而不采用任何金属五金件及胶粘剂，仅凭榫孔与榫头之间的紧密配合，就能达到理想的接合强度，这一工艺沿用至今。榫接合家具的受力情况多种多样，但通常对其力学性能进行评估时可分为抗拔、抗弯及抗扭转强度等，在相同的配合状态下，抗弯强度通常要小于抗拔强度及抗扭强度。故在榫接合家具结构设计时，节点抗弯强度占有重要地位。

现有对榫接合家具结构分析的主要方法是将其简化为二维平面结构，并应用力矩平衡的方法对其进行分析，或者通过有限次的力学试验总结出的经验方程对结构强度进行预测［1-2］。前者将三维结构的家具简化为二维结构，且忽略了节点的强度;而后者所得出的经验方程不具有普遍性。除此之外，众多学者针对榫接合节点抗弯强度的影响因素进行了研究。V.Zaborsky［3］等对影响节点抗弯强度的因素进行了研究，包括树种、节点形式、榫头尺寸、胶粘剂种类、纹理方向以及加载形式等，结果表明，木材种类、节点形式、榫头尺寸以及胶粘剂种类对构件的抗弯强度具有明显影响;而加载方式与纹理方向的影响却不明显。T.Bardak［4］等在 PVAc中加入 nano-TiO2和nano-SiO2对榫接合节点抗弯及抗拔强度的影响进行了研究，结果表明，当加入2%的nano-SiO2时，节点的抗弯及抗拔强度最大。高萃等［5］对不同棉秆重组方材家具部件结点接合结构的抗弯强度进行了研究。因此寻找一种系统性强，且能对三维家具结构进行准确分析的普遍方法成了研究者及家具结构设计师的关注点。

有限元分析法在家具结构力学的研究中应用较晚，到20世纪中后期［6-7］才被引入到家具设计中，研究内容集中于对有限元方法概念的引入［8-9］，通过个案对有限元法在家具结构力学的分析过程进行论述，研究对象涉及框架结构家具［10-13］，板式结构家具［14-18］以及其他木制品［19-21］，其为实现有限元法在家具结构分析中的应用奠定了一定基础，而对榫接合节点强度的分析及试验验证方法却很有限，仍需进一步进行研究。

本研究在无胶榫接合情况下，对榫接合节点抗弯强度的有限元分析方法进行了研究，并通过榫接合抗弯强度试验以及节点周围应变测量试验对有限元模型进行了验证。其是进一步建立榫接合胶合状态下有限元模型的基础。

1 材料与方法

1.1 材料及设备

试验材料为榉木(Fagus orientalis)，含水率11.91%～12.03%，气干密度0.689～0.71 g·cm－3。利用横截锯、纵截锯、压刨以及双面刨进行材料的粗加工;然后采用数控机床(原力WPC)进行榫头与榫孔的加工，试验设备为万能力学试验机(岛津AG-X)并结合自制辅助夹具。数据采集仪(TML TDS530)，应变片型号 BFH120-3AA0D100，电阻值为 120±1 Ω，基长×基宽为 6.9 mm×3.9 mm，栅长×栅宽为 3.0 mm×2.3 mm，材料为康铜，灵敏系数为2.0%×1%，应变片的粘贴采用502胶水。

1.2 试件制备

榫接合抗弯强度验试件为椭圆榫接合的T形构件，试件尺寸见图1，其中图1(a)为试件尺寸，图1(b)为榫头及榫孔尺寸。榫孔尺寸为30 mm(深度)×30 mm(高度)×16 mm(宽度)，榫头尺寸为30 mm(长度)×(30+a)mm(宽度)×15.8 mm(厚度)，加工偏差为±0.01 mm。其中榫头宽度与榫孔高度方向为过盈配合，配合量分别为0、0.1 mm 和0.2 mm，榫头宽度方向纹理为径向，榫头厚度方向与榫孔宽度方向为间隙配合，间隙为0.2 mm。

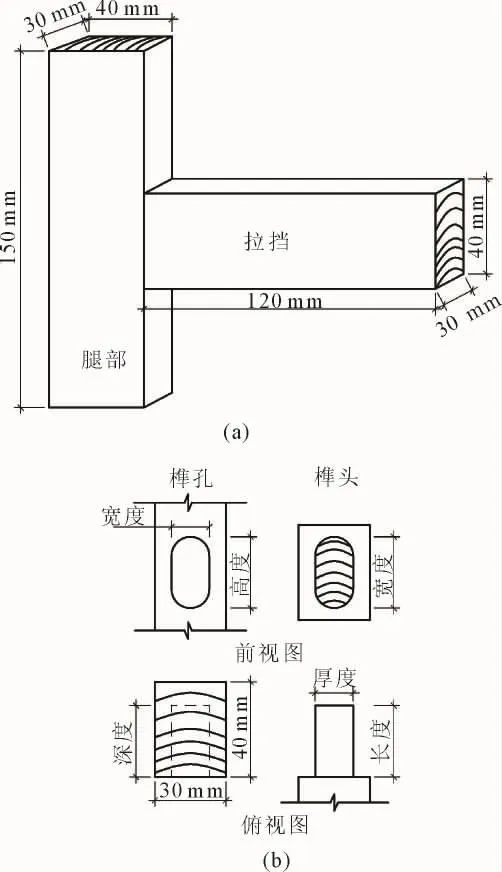
图1 榫接合试件及节点尺寸Fig.1 Dimensions of T-shaped specimen and joint

试件组装完毕后，于试件表面绘制15 mm×10 mm的网格，用于应变片的定位，并于距榫接合节点上下15mm处粘贴互相垂直的两组应变片，分别用于测量节点上下的应变情况(图2)，并与有限元分析结果进行对比分析。

图2 试件的网格划分及应变片粘贴位置Fig.2 Mesh of specimen and positions of plating strain gauges

1.3 抗弯强度测试方法

图3 为椭圆榫接合T形试件的加载示意图，于距节点90 mm处的拉挡上进行加载。为便于试验结果与有限元分析结果之间的对比，本研究中通过位移法进行加载，即当位移量达到30 mm时，停止加载，加载速度为10 mm·min－1。同时，采用1/4桥三线接法将应变片与数据采集仪进行连接，用于测量节点周围的应变情况。分别对不同过盈量(0、0.1、0.2 mm)接合的 T 形试件进行试验，每组重复10次测量，并记录下T形试件的位移-载荷数据以及节点的应变数据。

1.4 有限元分析法

本研究中通过ABAQUS有限元分析软件对T形试件的抗弯强度进行有限元分析。按图1中榫接合构件真实尺寸建立有限元模型，并按照图3抗弯强度测试的方法对有限元模型进行加载和边界条件约束，以保证有限元分析与试验情况尽量一致。在有限元模型建立过程中，将木材视为正交各项异性材料，并考虑了木材的塑性变形，材料参数已在前期研究［22］中测量(表1)。对椭圆榫节点采用如下处理方法，榫头与榫孔的圆弧表面采用过盈配合，而榫头与榫孔的平面部分为间隙配合，仅定义接触但不设置过盈配合。榫头与榫孔的圆弧接触部分定义摩擦关系，摩擦系数为 0.54，已于前期研究中进行测定［23］。并于加载头处施加30 mm的位移载荷，使榫头被缓慢拔出。设置完毕后进行分析。值得注意的是本研究中榫头宽度方向的纹理为径向，故在进行有限元模拟中应注意材料方向的定义，通过局部坐标赋予每个部件相应的纹理方向。

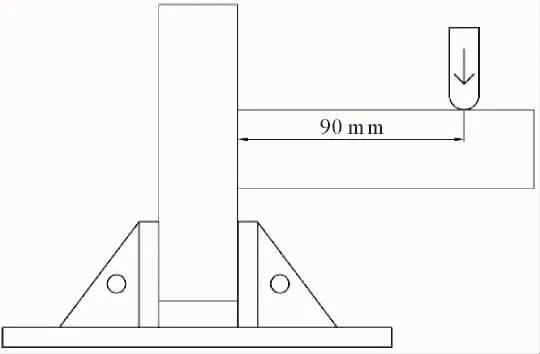
图3 抗弯强度的测试方法Fig.3 Method of measuring the bending resistance strength

表1 榉木力学参数Table 1 Mechanical properties of beech (N·mm－2)

2 结果与分析

2.1 有限元分析结果

图4为T形构件抗弯强度的有限元分析结果。其中图4(a)至4(d)分别为加载过程中构件表面的应力分布情况。由图可知构件在加载过程中榫孔下部与榫肩下部接触区域最易产生应力集中，同时榫头上表面在拉应力下产生断裂［图4(d)］。

图5为椭圆榫接合节点处的变形情况以及试验情况对比。其中图5(a)为有限元分析时榫孔处的应力分布情况，由图可知，在弯曲载荷作用下，榫头下部出现明显的塑性变形(灰色部分)，而榫孔上表面的应力则较小;图5(b)为试验过程中榫孔的变形情况，其中榫孔下部出现明显的压痕，并且榫孔下边缘出现了裂纹，因此可判断有限元分析结果与试验结果基本相符。图5(c)为有限元分析时榫头处的变形情况，榫头上表面受拉而下表面受压，并且榫头上表面出现明显的裂纹;图5(d)为试验过程中榫头的变形情况，榫头上表面出现了裂纹但并未断裂，总体变形情况与试验中的榫头变形情况一致。

2.2 抗弯强度对比分析

通过软件的后处理模块，输出有限元模型中加载头处的支反力-位移曲线，理论上其与试验机输出的载荷位移曲线应一致。图6分别为过盈量在0、0.1 mm以及0.2 mm时，试验结果与有限元分析结果的对比。由图可知，有限元分析结果与试验结果的位移-载荷曲线具有近似的趋势，但在局部存在差异，尤其是榫头产生裂纹时。其主要原因为有限元分析时，当应力达到材料的断裂强度，单元即会被删除，从而降低了构件的刚度，而在真实试验中，木材的断裂为韧性断裂，即使发生断裂，木纤维间也会相互作用，使木构件刚度不会骤降。

为详细比较有限元分析与试验结果之间的误差，以每5 mm位移为取样间距，分别提取相应位移处的载荷值进行比较(图7)。由图7可知，在不同的取样点，有限元分析结果与试验结果之间的误差也不同。其中，当过盈量为0 mm时，两者之间最大误差25%，最小误差1.56%，平均误差15.37%;当过盈量 0.1 mm 时，最大误差 23.44%，最小误差3.58%，平均误差 12.87%;而当过盈量 0.2mm时，最大误差23.95%，最小误差3.66%，平均误差11.25%。综上可得出有限元分析结果与试验结果的平均误差在20%之内，在工程允许范围内，可用于实木榫结合家具结构的设计中。

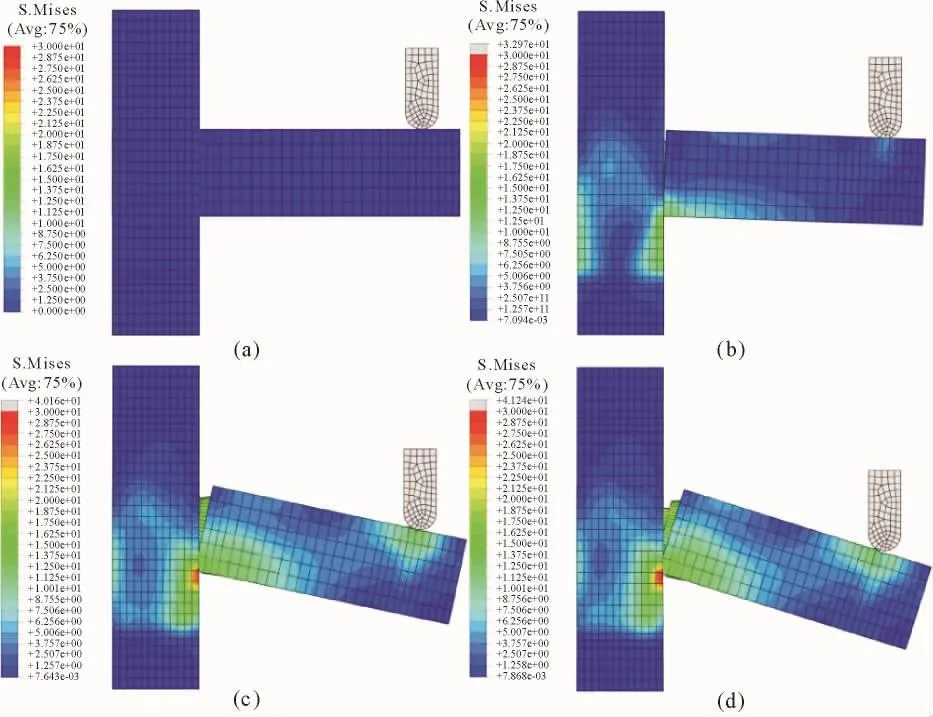
图4 试件应力分布Fig.4 Stress distribution of specimens

图5 节点变形情况对比Fig.5 Deformations comparison of joint

图6 抗弯强度对比Fig.6 Comparison of bending resistance strength

2.3 应变对比分析

对过盈量为0.2 mm时节点周围的应变进行了测量。在加载终点30 mm时，通过数据采集仪输出应变片粘贴位置的应变值。同时，通过有限元分析软件的后处理功能输出相应位置的应变随加载位移的变化过程见图8。

图7 误差分析Fig.7 Analysis of error

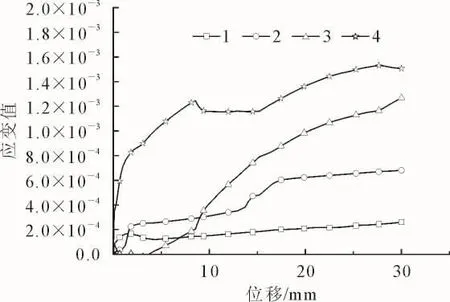
图8 有限元分析应变结果Fig.8 Results of strains based on FEM

图9 试验与有限元法节点周围应变对比Fig.9 Comparison of strains around the joint between experiment and FEM

分别在有限元模型中与应变片粘贴位置(1、2、3、4)相对应的单元处提取其应变值，并将其与试验结果进行对比(图9)。由图9可知，在应变片粘贴位置有限元分析结果与试验测量结果基本吻合，其进一步验证了本研究中所建立的有限元模型可用于榫接合节点抗弯强度的预测。

3 结论

本研究建立了无胶接合情况下，椭圆榫接合节点的抗弯强度有限元模型，并通过构件整体抗弯强度实验以及局部应变测量试验对其进行了验证。结果表明，本研究中所建立的有限元模型可用于榫接合节点抗弯强度的预测，同时，对节点周围应变的预测结果与试验结果吻合，进一步证实了本研究中所提出的有限元分析方法的准确性。其为实木榫接合家具的结构设计提供了有效的分析方法，对于优化家具设计流程具有重要意义。

在此研究基础之上，进一步将对胶接合情况下，榫接合节点强度的有限元分析方法进行研究，进而完善实木家具榫接合节点强度的有限元分析方法，缩短实木榫接合家具产品开发周期，降低成本。